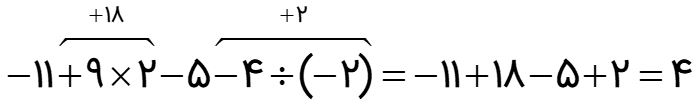درسنامه کامل ریاضی هفتم فصل 2 عددهای صحیح
تعداد بازدید : 7.27Mخلاصه نکات ریاضی هفتم فصل 2 عددهای صحیح - درسنامه شب امتحان ریاضی هفتم فصل 2 عددهای صحیح - جزوه شب امتحان ریاضی هفتم نوبت اول فصل 2 عددهای صحیح
عددهای علامت دار
در ریاضیات برای ساده و مختصر کردن بیان عددهای علامت دار از علامت های + و - استفاده می کنیم. برای تعیین علامت عددها نیاز داریم که محل مبدأ و واحد اندازه گیری و همچنین جهت های مثبت و منفی را قرارداد کنیم و براساس آن، عددها را علامت دار کنیم.
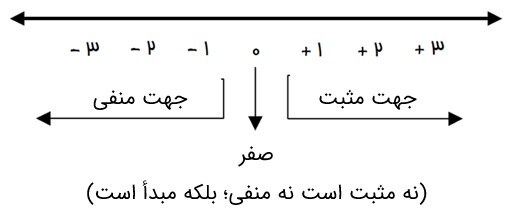
برای یکی شدن قراردادها، سمت راست را روی محور مثبت و سمت چپ را منفی در نظر می گیرند.
هر یک از عددهای … را عددهای صحیح می نامیم. «عدد صفر نه مثبت است و نه منفی.»
هرچه به سمت مثبت پیش می رویم عددها بزرگتر می شوند. بنابراین می توان نوشت: ۱ + > ۱ -
چند تا از عددهای مجموعه مقابل صحیح اند؟
\(\left\{ { - \frac{{2/4}}{6}\,,\, - 2\frac{4}{2}\,,\,\frac{5}{4}\,,\,0\,,\, - \frac{{1071}}{9}} \right\}\)
عددهای \(\left\{ { - 2\frac{4}{2},\,0\,,\, - \frac{{1071}}{9}} \right\}\) عددهای صحیح هستند.
بین 5- و 9+ چند عدد صحیح وجود دارد؟
تعداد عددهای صحیح بین دو عدد m و n که n>m برابر است با: 1 - m - n ؛ بنابراین:
13 = 1 – (5 + 9) = 1 – ((5–) – 9+)
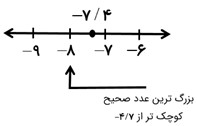
بزرگترین عدد صحیح کوجک تر از 7/4- کدام است؟
بزرگ ترین عدد صحیح کوچک تر از 7/4- عدد 8- است. همچنین می توان از محور اعداد نیز استفاده کرد:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
قرینه اعداد صحیح
قرينه هر عدد منفی، عددی مثبت و قرینه هر عدد مثبت، عددی منفی است. قرينه صفر هم خود صفر است. برای نمایش قرینه هر عدد از نماد ( - ) در سمت چپ آن عدد استفاده می کنیم.
8- = (8+)- = قرینه (8+)
5+ = (5-)- = قرینه (5-)
قرينه هر عدد صحیح را می توان با تغییر علامت آن عدد به دست آورد .
قرينه ی قرينه هر عدد صحيح، مساوی خودش است.
\(\begin{array}{l} - \left[ { - \,( - \,3)} \right] = - \,3\\\\ - \left[ { + \,( - \,6)} \right] = + \,6\end{array}\)
عددهای صحیح مثبت، همان عددهای طبیعی اند؛ برای مثال می توان نوشت:
\( + \,3 = 3\;\;\;\;\;,\;\;\;\;\; + 6 = 6\)
عددهای صحیح شامل عددهای صحیح مثبت ، صفر و عددهای صحیح منفی می شوند.
جمع هر عدد صحيح با قرینه اش برابر صفر می شود.
\(7\, - \,7 = 7 + \,(\, - \,7) = 0\)
جمع هر عدد صحیح با صفر برابر خودش می شود.
\(( - \,9) + 0 = - \,9\;\;\;\;\;\;,\;\;\;\;\;\;4 + 0 = 4\)
هر عدد صحیح مثبت از هر عدد صحیح منفی بزرگتر است.
همه عددهای صحیح مثبت از صفر بزرگ ترند.
همه عددهای صحیح منفی از صفر کوچکتر هستند.
قرینه عدد صفر نسبت به 2- کدام است؟
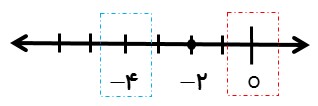
عدد قرینه 0 نسبت به 2- : \( \circ - ( - 2) = 2 \Rightarrow \,\, - 2 - (2) = - 4\)
قرینه قرینه قرینه عدد 10 کدام است؟
هر کلمه قرینه را با نماد – نشان می دهیم:
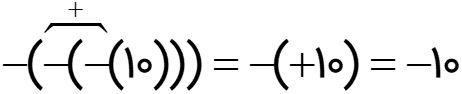
اگر عدد 25- را 1023 بار قرینه کنیم، نتیجه حاصل چه عددی می شود؟
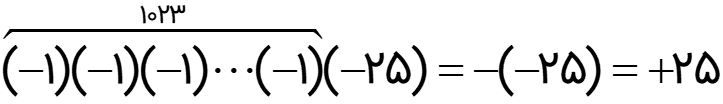
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
حرکت روی محور عددهای صحیح
شامل دو بخش زیر است:
الف) جهت:
حرکت به سمت راست مثبت +، حرکت به سمت چپ -، در جای خود حرکت 0 (صفر).
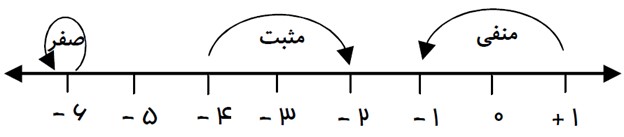
ب) اندازه:
به مقدار جابجایی که با عدد نشان داده می شود.
اگر متحرکی فاصله 4- تا 6+ را در 20 ثانیه طی کند، فاصله 5- تا 20- را در چند ثانیه طی هواهد کرد؟
منظور از فاصله، مسافت طی شده توسط متحرک است که برابر است با:
عدد مبدأ – عدد مقصد = فاصله
10+ = (4–) – 6+ : فاصله 4– تا 6+
15– = (5–) – (20–) : فاصله 5– تا 20–
10+ یعنی 10 واحد جلو رفته و 15– یعنی 15 واحد به عقب برگشته است:
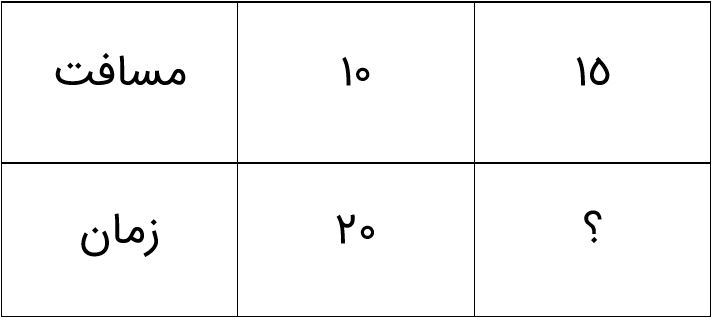
ثانیه \(?\,\, = \,\frac{{20 \times 15}}{{10}} = 30\)
بردار 5- ابتدا در 1- را رسم کنید.
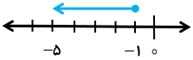
از نقطه 10+ برداری را که انتهای آن نقطه 3+ است، رسم می کنیم. اگر انتهای بردار را به 1+ منتقل کنیم، باید بردار را از چه نقطه ای رسم کنیم؟
ابتدا خود بردار (اندازه و جهت) را به دست می آوریم:
\(\,\, = ( + 3) - ( + 10) = - 7\) اندازه بردار <= ابتدا – انتها = اندازه بردار
سپس انتهای بردار را جا به جا می کنیم و ابتدای بردار جدید را به دست می آوریم:
<= ابتدا – انتها = بردار \( - 7 = + 1 - \)ابتدا
ابتدا – \( = - 7 - 1 = - 8\)
\( = 8\)ابتدا
جمع عددهای صحیح روی محور
اگر دو یا چند حرکت روی محور پشت سر هم انجام گیرد، می توان برای این حرکات یک تساوی جمع نوشت:
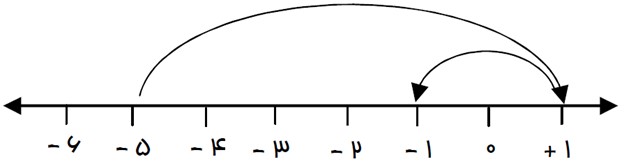
\(( + \,6) + ( - \,2) = ( + \,4)\)
مثال
جمع متناظر نمودار زیر را بنویسید و بدست آورید.
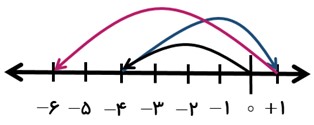
جمع متناظر نمودار بالا به صورت زیر است:
\(( - 4) + ( + 5) + ( - 7) = - 6\)
برای جمع زیر نمودار متناظر را نوشته و جواب را بدست آورید.
\(( + \,6) + ( - \,2) + ( - 3) = \)
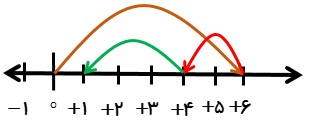
\(( + \,6) + ( - \,2) + ( - 3) = + 1\)
جمع و تفریق عددهای صحیح (بدون محور):
باید گام های زیر را به ترتیب انجام داد:
گام اول، مختصر یا ساده نویسی:
پرانتزها را حذف کنید.
گام دوم، تعیین علامت:
اگر قبل از عددی بیش از یک علامت وجود داشت ، باید به کمک عمل ضرب آنها را به یک علامت تبدیل کنید.
\(\begin{array}{l} - \,( - \,7) = + \,7\\\\ + \,( - \,2) = - \,2\end{array}\)
برای این کار از جدول داده شده کمک بگیرید:
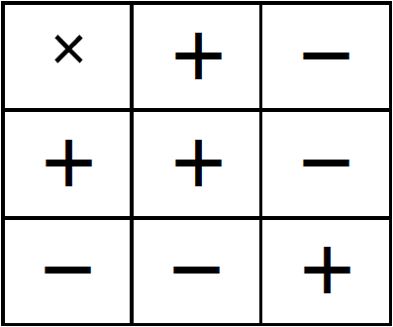
گام سوم، تعیین علامت حاصل:
پس از مختصر نویسی و تعیین علامت عددهای صحیح نوبت به یافتن علامت جواب (حاصل) می باشد. اگر هر دو علامت یک جور بود ، یک علامت را برای جواب قرار داده و عددها را جمع می کنیم:
\(\begin{array}{l}8 - \,( + \,7) = 8\, - \,7 = + \,1\\\\( - \,12) + \,( - \,7) = - \,12\, - \,7 = - \,19\end{array}\)
اگر علامت ها یک جور نبود، علامت عدد ظاهراً بزرگتر را برای جواب قرار داده و عددها را از هم کم می کنیم:
\(\begin{array}{l}8 - \,( - \,7) = 8\, + \,7 = + \,15\\\\( - \,18) + \,( + \,11) = - \,18\, + \,11 = - \,7\end{array}\)
مثال
حاصل عبارت \(( - 1) - ( - 2) - ( - 3) - ( - 4) - ( - 5)\) را بدست آورید.
\(\begin{array}{l}( - 1) - ( - 2) - ( - 3) - ( - 4) - ( - 5) = \\\\( - 1) + 2 + 3 + 4 + 5 = 13\end{array}\)
قرینه حاصل عبارت \( - \left[ {\left( { + 14} \right) - \left( { - 2} \right) - \left( {10} \right) + \left( { - 4} \right)} \right]\) را بدست آورید.
\(\begin{array}{l} - \left[ {\left( { + 14} \right) - \left( { - 2} \right) - \left( {10} \right) + \left( { - 4} \right)} \right] = \\\\ - \left[ {\underline { + 14 + 2} \,\,\,\,\underline { - 10 - 4} } \right] = - \left[ { + 16 - 14} \right] = - 2\end{array}\)
قرینه 2- نیز 2+ می باشد.
جمع و تفریق عددهای صحیح (به روش ارزش مکانی):
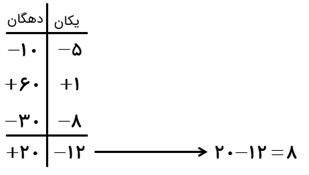
در این روش هر عدد را به همراه علامتش در جدول ارزش مکانی نوشته، با تبدیل آن به یک عبارت، حاصل را به دست می آوریم:
\( - \,15\, + \,61\, - \,38\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هفتم- آزمون آنلاین تمامی دروس پایه هفتم
- گام به گام تمامی دروس پایه هفتم
- ویدئو های آموزشی تمامی دروس پایه هفتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هفتم
- فلش کارت های آماده دروس پایه هفتم
- گنجینه ای جامع از انشاء های آماده پایه هفتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هفتم
ضرب عددهای صحیح به کمک محور
از دستور زیر می توان به سادگی به پاسخ رسید:
\(( - \,2)\, \times 3 = - \,6\)
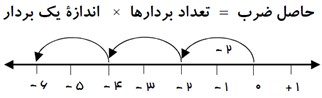
مثال
ضرب متناظر با محور مقابل را بیابید.
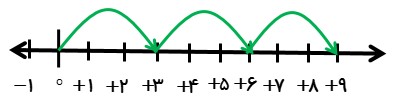
ضرب متناظر آن به صورت زیر است:
\(( + 3)\, \times 3 = + 9\)
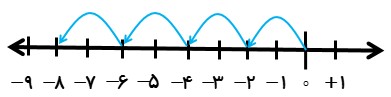
نمودار متناظر با ضرب زیر را بنویسید و حاصل را بدست آورید.
\(( - 2)\, \times 4 = \)
نمودار متناظر با ضرب به صورت زیر می شود:
ضرب و تقسیم عددهای صحیح
برای ضرب و تقسیم عددهای صحیح نیز باید دو گام زیر را به ترتیب انجام داد:
گام اول، تعیین علامت حاصل:
اگر علامت ها یک جور بود، علامت حاصل مثبت + و اگر همسان نبود، علامت حاصل منفی خواهد شد.
گام دوم، بدست آوردن جواب:
پس از تعیین علامت، عددها را در هم ضرب یا بر هم تقسیم کنید.
\(( - \,18)\, \div ( + \,3) = - \,6\)
مثال
حاصل عبارت های زیر را بدست آورید.
\(\begin{array}{l}1)\,\,\,( - 100) \div ( + 10) = \\\\2)\,\,( - 4) \times ( + 25) = \\\\3)\,{\kern 1pt} ( - 2) \times ( - 3) \div ( + 6) = \end{array}\)
\(\begin{array}{l}1)\,\,\,( - 100) \div ( + 10) = - 10\\\\2)\,\,( - 4) \times ( + 25) = - 100\\\\3)\,{\kern 1pt} ( - 2) \times ( - 3) \div ( + 6) = ( + 6) \div ( + 6) = + 1\end{array}\)
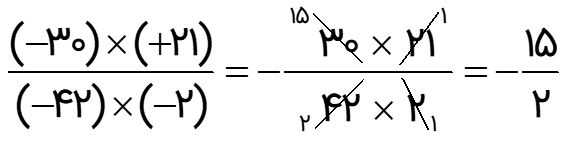
حاصل عبارت \(\frac{{( - 30) \times ( + 21)}}{{( - 42) \times ( - 2)}}\) را بدست آورید.
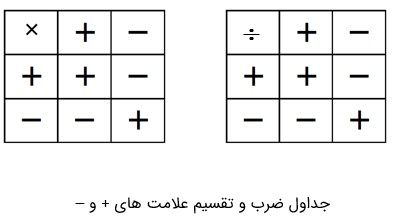
باید در ساده کردن این طور کسرها دقت کرد. با توجه به جدول ضرب و تقسیم برای علامت های + و – داریم:
عبارت های ترکیبی
در حل این عبارت ها ابتدا پرانتز (کروشه) را محاسبه و سپس با توجه به علامت بین عددها، حاصل را به دست می آوریم. اگر در یک عبارت ترکیبی پرانتز (کروشه) وجود نداشت، طبق اولویت علامت ها از سمت چپ: یعنی ضرب، تقسیم، جمع و تفریق را انجام دهید:
مثال
حاصل عبارت زیر را بدست آورید.
\(\frac{{ - 30 + 40 - 50 + 60 - \cdots - 210 + 220}}{{ - 150 + 200 - 250 + 300 - \cdots - 1050 + 1100}} = \)
صورت و مخرج کسر را به صورت زیر دسته بندی می کنیم:
\(\begin{array}{l}\frac{{( - 30 + 40) + ( - 50 + 60) + \cdots + ( - 210 + 220)}}{{( - 150 + 200) + ( - 250 + 300) + \cdots + ( - 1050 + 1100)}} = \\\\\frac{{10 + 10 + \cdots + 10}}{{50 + 50 + \cdots + 50}} = \frac{{10 \times 10}}{{50 \times 10}} = \frac{{10}}{{50}} = \frac{1}{5}\end{array}\)
حاصل عبارت \( - \left[ {5\frac{ \circ }{2} \times 3\frac{4}{4} - 12\frac{{48}}{{24}} \times 6\frac{6}{6}} \right]\) را بدست آورید.
دقت کنید عددهایی مانند \(3\frac{4}{4}\) عددهای مخلوط اند که بین عدد و کسر، علامت جمع (به صورت پنهان) وجود دارد:
\(\begin{array}{l}5\frac{ \circ }{2} = 5 + \frac{ \circ }{2} = 5 + \circ = 5\\\\3\frac{4}{4} = 3 + \frac{4}{4} = 3 + 1 = 4\\\\12\frac{{48}}{{24}} = 12 + \frac{{48}}{{24}} = 12 + 2 = 14\\\\6\frac{6}{6} = 6 + \frac{6}{6} = 6 + 1 = 7\\\\ - \left[ {5\frac{ \circ }{2} \times 3\frac{4}{4} - 12\frac{{48}}{{24}} \times 6\frac{6}{6}} \right] = - \left[ {5 \times 4 - 14 \times 7} \right] = \\\\ - \left[ {20 - 98} \right] = - ( - 68) = + 68\end{array}\)
جزوات جامع پایه هفتم
جزوه جامع ریاضی هفتم فصل 1 راهبردهای حل مسئله
جزوه جامع ریاضی هفتم فصل 2 عددهای صحیح
جزوه جامع ریاضی هفتم فصل 3 جبر و معادله
جزوه جامع ریاضی هفتم فصل 4 هندسه و استدلال
جزوه جامع ریاضی هفتم فصل 5 شمارنده ها و اعداد اول
جزوه جامع ریاضی هفتم فصل 6 سطح و حجم
جزوه جامع ریاضی هفتم فصل 7 توان و جذر
جزوه جامع ریاضی هفتم فصل 8 بردار و مختصات
جزوه جامع ریاضی هفتم فصل 9 آمار و احتمال
حل مسائل به کمک عددهای صحیح
گروه اول:
اگر در مسئله ای اختلاف یا فاصله، مانند سردتر، گرمتر و ... خواسته شد، از دستور زیر استفاده کنید:
عدد کوچکتر - عدد بزرگتر = اختلاف
مثال
دمای هوای تهران ۲۸ درجه بالای صفر است. اردبیل ۸ درجه زیر صفر است. اختلاف دمای هوای دو شهر چند درجه است؟
\(( + \,28)\, - \,( - \,8) = 28\, + \,8 = 36\)
گروه دوم:
اگر در مسئله ای میانگین عددها خواسته شد، ابتدا عددها را با هم جمع و سپس حاصل را بر تعداد آنها تقسیم کنید.
مثال
دمای هوا در تبریز دو درجه زیر صفر و دمای اردبیل ۳ برابر آن است. میانگین دمای این دو شهر چند درجه است؟
\(\begin{array}{l}( - \,2) \times 3 = \, - \,6\\\\( - \,6)\, + \,( - \,2) = - \,6\, - \,2 = - \,8\\\\ - \,8\, \div \,2 = - \,4\end{array}\)
گروه سوم:
اگر در مسئله ای هیچ کدام از حالت های قبل وجود نداشت، بین عددها علامت جمع قرار دهید.
مثال
دمای هوای شهر کرد ۳ درجه زیر صفر است. اردبیل ۸ درجه از شهرکرد سردتر است. دمای هوای شهر اردبیل چند درجه است؟
\(( - \,3)\, + \,( - \,8) = - \,11\)



1736019749.png)