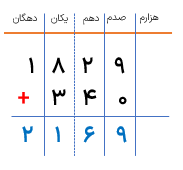
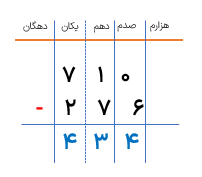
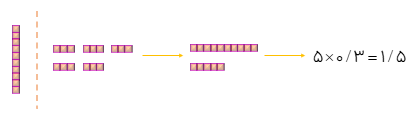
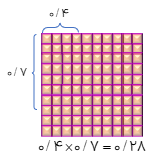
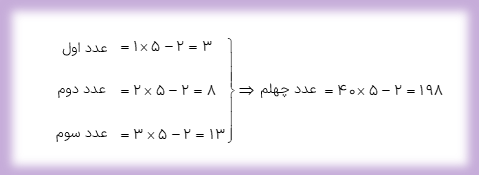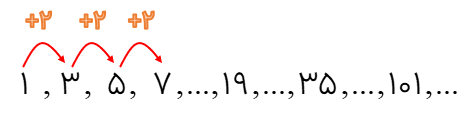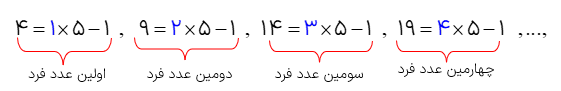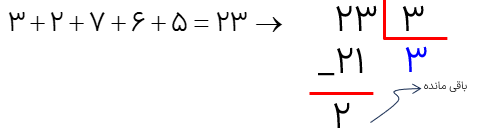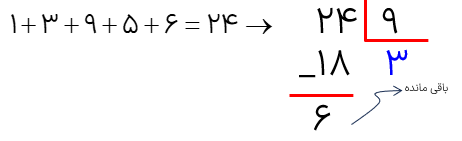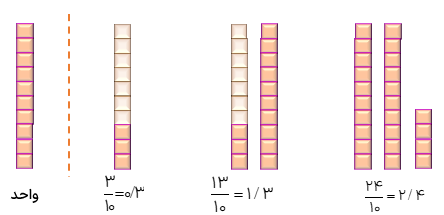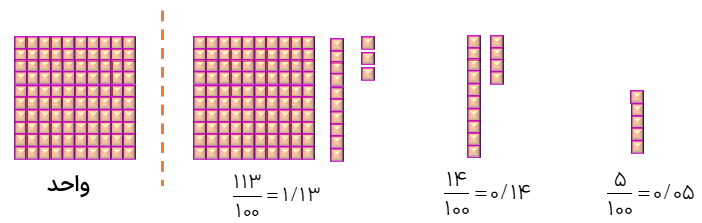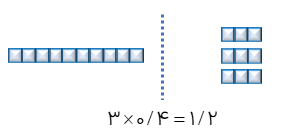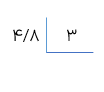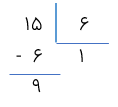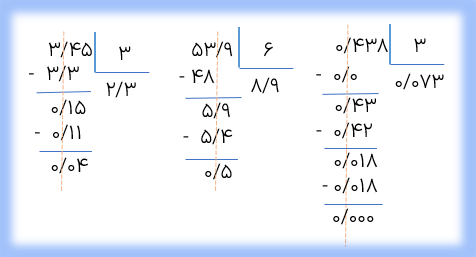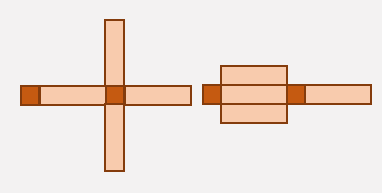درسنامه کامل ریاضی ششم
تعداد بازدید : 301.22kخلاصه نکات ریاضی ششم - درسنامه شب امتحان ریاضی ششم - جزوه شب امتحان ریاضی ششم نوبت اول
الگوهای عددی
فصل 1 : عدد و الگوهای عددی
الگوهای عددی
در شکل مقابل ۱۲ ستاره هست آنها را به دسته های دوتایی تقسیم میکنیم همان طور که مشاهده می کنید، تمام ستاره ها در دسته های دوتایی قرار گرفته اند و هیچ ستاره ای باقی نمانده است.
عدد ۱۲، عدد زوج است زیرا اگر ۱۲ تا قلم یا ۱۲ تا دفتر یا ۱۲ تا ستاره داشته باشیم می توانیم آن ها را به دسته های دوتایی تقسیم کنیم، بدون اینکه قلم یا دفتر یا ستارهای خارج از دسته های دوتایی داشته باشیم.
مثال
می دانیم که هر انسان دو دست است. جدول زیر رابطه ی بین تعداد انسان ها و تعداد دست های آن ها را نشان می دهد:
طبق رابطه ای که در جدول بالا وجود دارد می توانیم بنویسیم:
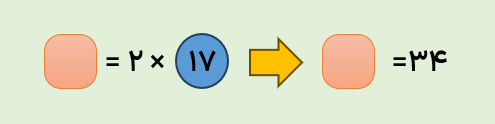
تعداد انسان ها × ۲ = تعداد دست ها
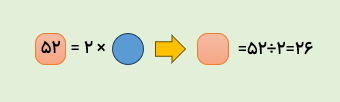
اگر تعداد انسان ها را با دایره و تعداد دست ها را با مربع نشان دهیم، رابطه ی بالا به صورت زیر در می آید.
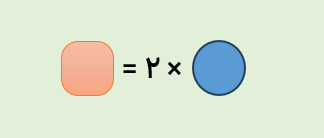
الف انسان روی هم چند دست دارند؟
ب52 دست برای چند انسان است؟
به عدد های ... و ۵ و ۴ و ۳ و ۲ و ۱ عددهای طبیعی می گویند.
به عددهای ... و ۱۲ و ۱۰ و ۸ و ۶ و ۴ و ۲ عددهای زوج یا مضرب های عدد ۲ می گویند.
مضرب ۲ یعنی عددی که بر ۲ بخش پذیر است.
از ضرب عددهای طبیعی در عدد ۲ عددهای زوج حاصل می شود.
در عددهایی که بیش از یک رقم ،دارند اگر رقم سمت راست ، عدد ۲,۰، ۴، ۶ یا ۸ ،باشد، به آن عددها، عددهای زوج می گوییم مانند ۷۳۳۴ - ۲۱۸ - ۳۷۵۶
مثال
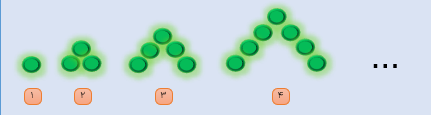
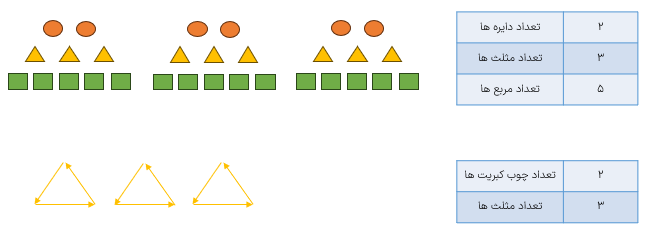
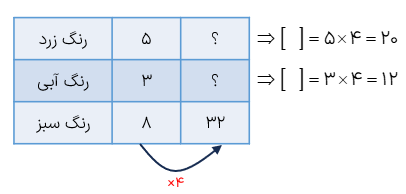
با توجه به الگویی که در شکل زیر هست جدول زیر را کامل کرده ایم.
الف شکل شماره ی ۲۳ دارای چند دایره است؟
23×2-1=45
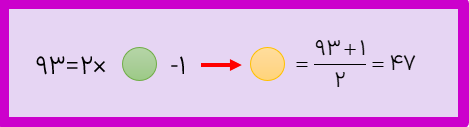
ب شماره ی شکلی که دارای ۹۳ دایره است، چند است؟
1 اگر شماره ی شکل را با مربع و تعداد دایره ها را با دایره نمایش دهیم رابطه ی بین تعداد دایره ها و شماره ی شکل به صورت زیر است.
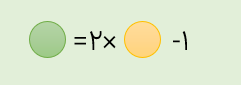
2 به عددهای ... و ۱۱ و ۹ و ۷ و ۵ و ۳ و ۱ عددهای فرد می گوییم. هر عدد طبیعی که زوج نباشد فرد است.
به جدول زیر دقت کنید.
همان طور که می بینید عددهای سطر پایین مضرب های ۳ هستند؛ یعنی عددهایی که بر ۳ بخش پذیرند از ضرب عددهای طبیعی در ۳ مضرب های ۳ حاصل می شوند.
1 عددهای ... و ۲۵ و ۲۰ و ۱۵ و ۱۰ و ۵ را مضرب های ۵ می گویند. مضرب های ۵ بر ۵ بخش پذیر هستند.
2 کوچک ترین مضرب هر عدد، خود آن عدد است.
مثال
به الگوی زیر که با چوب کبریت ساخته شده، دقت کنید.
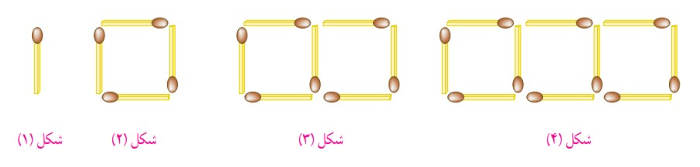
الگوی عددی مقابل تعداد چوب کبریت های شکل بالا را نشان می دهد.
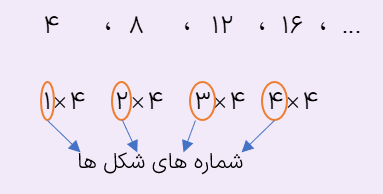
این الگوی عددی مضرب های ۴ را نشان میدهد چون تعداد چوب کبریت های هر شکل ۴ برابر عدد شماره ی آن شکل است، پس بین آن ها تناسب برقرار است.
الف در شکل هفتم چند چوب کبریت وجود دارد؟
به ضرب های مقابل دقت کنید.
۱×۱۲ = ۱2
۲×۶ = ۱۲
۳×۴ =۱۲
با توجه به تساوی های بالا می فهمیم که ۱۲ مضرب عددهای ۱، ۲، ۳، ۴، ۶ و ۱۲ است.
مثال
عدد ۱۸ مضرب چه عددهایی می تواند باشد؟
عدد ۱۸ مضرب عددهای ۱، ۲، ۳، ۶، ۹ و ۱۸ است.
۱ × ۱۸ = ۱۸
۲×۹ = ۱۸
۳×۶ = ۱۸
سه عدد بعدی الگوی عددی زیر را بنویسید و سپس عدد چهلم این الگو را بیابید.
... و ۱۸ و ۱۳ و ۸ و ۳
... و ۳۳ و ۲۸ و ۲۳ و ۱۸ و ۱۳ و ۸ و ۳
چون با اضافه کردن ۵ واحد به هر یک از عددهای الگو عدد بعدی به دست می آید بنابراین اعداد الگو با مضرب های ۵ ارتباط دارند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
الگو یابی
فصل 1 : عدد و الگوهای عددی
الگویابی
در سال های قبل با مفهوم الگویابی آشنا شده اید و آموختید که الگویابی یکی از ابزارهایی است که می توانیم از آن برای حل یک مسئله استفاده کنیم.
مثال
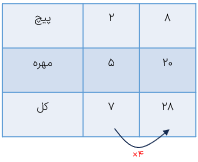
وسیله ی مقابل ریکشا نام دارد از این وسیله در کشور هند برای جابه جایی مسافران داخل شهر استفاده می شود. همان طور که ملاحظه میکنید این وسیله دارای سه چرخ است. با تشکیل جدول زیر می توانیم رابطه ی بین تعداد ریکشاها و همچنین تعداد چرخ ها را بیابیم.
با دقت در جدول زیر نتیجه میگیریم که هیچ گاه تعداد چرخ ها از ۵ یا ۷ یا ۸ چرخ نمی شود و همواره تعداد چرخ ها باید بر ۳ بخش پذیر باشد.
در مثال بالا به عددهای ۳ و ۶ و ۹ و ... مضرب های عدد ۳ گفته می شود.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
مضرب
فصل 1 : عدد و الگوهای عددی
مضرب
از ضرب هر عدد طبیعی در عددهای ۱ و ۲ و ۳ و ... مضرب های آن عدد ساخته میشود. بنابراین مضرب های هر عددی همواره بر آن عدد بخش پذیر هستند.
مضرب های7 :\(7 \times 1\,\,,\,7 \times 2\,,\,7 \times 3\,,\,7 \times 4,... \to 7,14,21,28,...\)
مضرب های4 :\(4 \times 1\,,\,4 \times 2\,,\,4 \times 3\,,\,4 \times 4\,,\,...\,,\, \to 4,8,12,16,...\)
.\(20 \times \,1\,,\,20 \times 2\,,\,20 \times 3\,,\,20 \times 4\,,\,...\,,\, \to 20,40,60,80,...\) :مضرب های ۲۰
1 کوچک ترین مضرب هر عددی برابر خود آن عدد و بزرگ ترین مضرب آن عدد، نامعلوم است.
2 عددهای زوج همان مضرب های ۲ هستند.
... و ۸ و ۶ و ۴ و ۲ : عددهای زوج
اعداد زوج و فرد
به الگوی عددی زیر توجه کنید:
به این اعداد عددهای فرد میگوییم با دقت در این عددها ملاحظه می کنید که اگر به هر یک از این عددها ۲ واحد اضافه کنیم عدد بعدی آن به دست می آید؛ یعنی فاصله ی هر عدد با عدد قبل و یا بعد از خودش مساوی ۲ واحد است لذا برای پیدا کردن رابطهی هر عدد فرد و شماره ی آن عدد میتوانیم از مضرب های ۲ کمک بگیریم:
مثال
با توجه به الگوی ،زیر، به سؤالات پاسخ دهید.
الف شکل پنجم چه عددی را نشان میدهد؟
این شکل،ها الگوی عددی روبه رو را نشان می دهند:
.... و ۱۹ و ۱۴ و ۹ و ۴
به هر شکل ۵ مربع اضافه شده تا شکل بعدی آن به دست آمده است. به این ترتیب در شکل پنجم، ۲۴ = ۵ + ۱۹ مربع وجود دارد در این سؤال با توجه به اینکه فاصله ی بین هر عدد با عدد بعد از خودش ۵ واحد است برای پیدا کردن رابطه ی بین هر عدد و شماره ی آن عدد میتوانیم از مضرب های ۵ کمک بگیریم.
ب برای ساختن شکل بیستم به چند عدد توپ نیازمندیم؟
با توجه به رابطه ی بالا برای ساختن شکل بیستم:
۹۹ = ۱- ( ۵ × ۲۰ ) = تعداد توپ ها در شکل بیستم
ج آیا شکلی دقیقا با ۳۰ عدد توپ ساخته می شود؟
با توجه به اینکه عددهای ۴ ,۹ ,۱۴ ,۱۹ و ... همواره یک واحد از مضرب های ۵ کم تر هستند و ۳۰ دقیقا مضرب ۵ است. دقیقا با ۳۰ عدد توپ نمی توان هیچ شکلی با توجه به این الگو ساخت.
1 مجموع دو عدد زوج همواره عددی زوج است.
2 مجموع دو عدد فرد همواره عددی زوج است.
3 مجموع هر عدد زوج با هر عدد فرد همواره عددی فرد است.
عدد نویسی
فصل 1 : عدد و الگوهای عددی
عدد نویسی
پیش از این با جدول ارزش مکانی آشنا شده اید برای خواندن عدد ۲۰۱۶۱۳۹۴ این عدد را در جدول ارزش مکانی قرار می دهیم.
ارزش مکانی رقم ۲ دهگان میلیون است که در این عدد هشت رقمی بیشترین ارزش مکانی را دارد.
ارزش مکانی رقم ۶ دهگان هزار است.
ارزش مکانی رقم ۳، صدگان است.
هر چه قدر به سمت راست جدول ارزش مکانی حرکت کنیم ارزش مکانی رقم ها کم تر می شود.
عدد ۲۰۱۶۱۳۹۴ خوانده میشود: بیست میلیون و صد و شصت هزار و سیصد و نود و چهار.
مثال
عدد ۹۸۷۶۵۳۴۲۱۰ را به حرف بنویسید.
ابتدا عدد را از سمت راست سه رقم سه رقم دسته بندی میکنیم و سپس با توجه به طبقه ی آن ها، عدد را می خوانیم.
9 ۸۷۶ ۵۳۴ ۲۱۰
نه میلیارد و هشتصد و هفتاد و شش میلیون و پانصد و چهل و سه هزار و دویست و ده.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
گسترده نویسی اعداد
فصل 1 : عدد و الگوهای عددی
گسترده نویسی اعداد
مثال
گسترده ی عدد 395 را بنویسید.
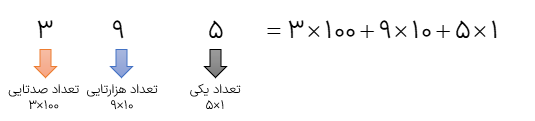
مثال
گسترده ی عدد ۴۹/۱۵۶ را بنویسید.
\(49/156 = 4 \times 10 + 9 \times 1 + 1 \times 0/1 + 6 \times 0/001\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
مقایسه ی عددهای صحیح
فصل 1 : عدد و الگوهای عددی
مقایسه ی عددهای صحیح
برای مقایسه ی دو عدد، ابتدا به تعداد رقم های آنها توجه میکنیم هر عددی که تعداد رقم هایش بیشتر باشد، بزرگ تر است.
۱۰۰۰۰>۹۸۷۶
در صورت مساوی بودن تعداد رقم ها از اولین رقم سمت چپ رقمی که بیشترین ارزش مکانی را دارد مقایسه را شروع میکنیم و به سمت راست حرکت میکنیم تا به رقمهای دارای ارزش مکانی مساوی و مقدارهای متفاوت برسیم.
مثال
دو عدد ۹۵۰۷۴۹۳ و ۹۵۰۷۵۹۸ را با هم مقایسه کنید.
۹۵۰۷۵۹۸ > ۹۵۰۷۴۹۳
مثال
1 بزرگ ترین عدد چهار رقمی را بنویسید.
۹۹۹۹
2 بزرگ ترین عدد چهار رقمی بدون تکرار رقم ها را بنویسید.
۹۸۷۶ (به ترتیب قرار گرفتن رقم ها دقت کنید)
3 کوچک ترین عدد پنج رقمی را بنویسید.
۱۰۰۰۰
4 کوچکترین عدد پنج رقمی بدون تکرار رقم ها را بنویسید.
۱۰۲۳۴ ( به ترتیب قرار گرفتن رقم ها دقت کنید)
5 با رقم های ۰ و ۱ و ۲ کوچکترین عدد هفت رقمی زوج را بنویسید.
۱۰۰۰۰۰۲
توجه کنید که اگر رقم ۲ غیر از مرتبه ی یکان در هر مرتبه ای قرار می گرفت، دیگر عدد کوچک ترین نمی شد.
جدول ارزش مکانی
فصل 1 : عدد و الگوهای عددی
جدول ارزش مکانی
در سال های گذشته با نوشتن اعداد به رقم و حروف جایگذاری رقمهای یک عدد در جدول ارزش مکانی وهمچنین خواندن آنها و سپس گسترده نویسی عددها آشنا شدید که در اینجا به یادآوری آن ها می پردازیم.
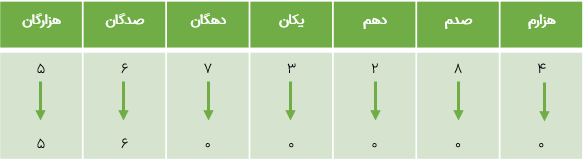
در این جدول بالاترین ردیف نشان دهنده ی طبقه ی اعداد است. همچنین منظور از حرف ی همان یکان و حرف د همان دهگان و حرف ص همان صدگان می باشد.
در یک جدول ارزش مکانی ممکن است نام طبقه ی یکی ها نوشته نشود.
برای خواندن یک عدد از روی جدول ارزش مکانی کافی است که از بزرگترین طبقه شروع کنیم و عدد مربوط به هر طبقه را نوشته و پس از آن نام طبقه را به همراه یک و بنویسیم در ضمن نام طبقه ی یکی، نوشته نمی شود. به این ترتیب عدد موجود در جدول بالا را به صورت زیر می خوانیم:
بیست و هفت میلیارد و چهار میلیون و شصت و سه هزارو دو «و» سی و چهار هزارم
در عدد بالا بزرگ ترین رقم یکان میلیارد می باشد.
با ارزش ترین رقم هر عدد اولین رقم در سمت چپ آن و کم ارزش ترین رقم هر عدد، اولین عدد سمت راست آن عدد می باشد.
۲۷۰۰۴۰۶۳۰۰۲/۰۳۴
کم ارزش ترین رقم (اولین رقم سمت راست) =4
با ارزش ترین رقم (اولین رقم سمت چپ=2
برای تعیین طبقه یا مرتبه ی یک رقم در یک عدد بهتر است که آن عدد را در یک جدول ارزش مکانی قرار دهیم. البته می توانیم بدون جدول هم این کار را انجام دهیم به این ترتیب که از سمت راست و از یکان عدد سه رقم جدا کنیم و بین قسمت های جدا شده علامت و قرار دهیم تا عدد مربوطه به هر طبقه مشخص شود.
مثال
عدد ۸۳۵۰۰۱۷۳۴۶/۵۲۸۱ را با حروف بنویسید. سپس مرتبه ی هر یک از ارقام ۷، ۴ و ۲ را مشخص کنید.
ابتدا از یکان عدد ( یعنی ۶) به سمت چپ سه رقم سه رقم جدا می کنیم:
\(8350017346/5281 \to 8\,,\,350\,,\,017\,,\,346/5\,,\,281\)
پس عدد فوق را به صورت زیر می نویسیم و می خوانیم:
هشت میلیارد و سیصد و پنجاه میلیون و هفده هزار و سیصد و چهل و شش و پنج هزار و دویست و هشتاد و یک هزارم
رقم ۷ در مرتبه ی یکان طبقه ی ،هزار رقم ۴ در مرتبه ی دهگان طبقه ی یکی و رقم ۲ در مرتبه ی صدم طبقه ی اعشاری قرار دارد.
در نوشتن یک عدد با یک تعداد رقم داده شده رقم صفر نمیتواند با ارزش ترین مکان یعنی اولین رقم سمت چپ عدد قرار بگیرد چون صفر پشت عدد، خوانده نمی شود.
جدول ارزش مکانی مربوط به نمایش یک عدد را میتوانیم به صورت زیر هم نمایش دهیم و با استفاده از این جدول هر عددی را به صورت گسترده ی آن هم بنویسیم به این ترتیب که عدد مورد نظر را در جدول جایگذاری نموده و به ترتیب رقم های آن را با توجه به مرتبهی آنها با هم جمع کنیم دقت داشته باشید که اگر رقم مربوط به یکی از مرتبه،ها صفر ،باشد آن را در گسترده ی عدد نمی نویسیم.
مثال
عدد ۴۳۵۰۷۰۱۸/۰۴۹ را به صورت گسترده بنویسید.
ابتدا عدد را در جدول ارزش مکانی جایگذاری میکنیم و به ترتیب هر رقم را در مرتبه ی آن ضرب نموده و در آخر همگی آن ها با هم جمع می کنیم.
\( \Rightarrow 40000000 + 3000000 + 500000 + 70000 + 10 + 8 + 0/04 + 0/009\) گسترده ی عدد
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نمایش تقریبی اعداد روی محور
فصل 1 : عدد و الگوهای عددی
نمایش تقریبی اعداد روی محور
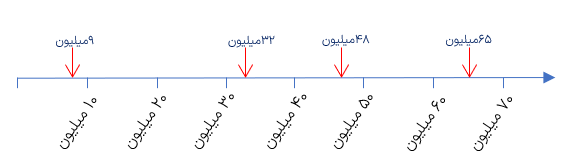
در سال های قبل با نمایش تقریبی اعداد با تقریبهای دهگان صدگان هزارگان و ... آشنا شدید. در این درس می خواهیم شما را با نمایش تقریبی با تقریب های خیلی بزرگ مانند ده میلیون و بزرگ تر از آن آشنا کنیم. به مثال های زیر دقت کنید.
از آن جا که در محور بالا تقریب با رقم دهگان میلیون مورد نظر است برای نمایش عددی مانند ۴۷۸۶۳۷۰۲ بهتر است ابتدا آن را به صورت تقریبی ۴۸۰۰۰۰۰۰ یا همان ۴۸ میلیون بنویسیم سپس محل تقریبی این عدد را با یک فلش روی محور نمایش دهیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
بخش پذیری
فصل 1 : عدد و الگوهای عددی
بخش پذیری
اگر بخواهیم ۱۴ سیب را بین دو نفر تقسیم کنیم، به هر کدام ۷ سیب میرسد و سیبی باقی نمی ماند. بنابراین میگوییم عدد ۱۴ بر ۲ بخش پذیر است.
اگر ۲۶ شکلات را بین دو نفر تقسیم کنیم به هر یک ۱۳ شکلات میرسد و شکلاتی باقی نمی ماند، بنابراین می گوییم ۲۶ بر ۲ بخش پذیر است.
1 عددی بر ۲ بخش پذیر است که رقم یکان آن 2,0 ، ۴، ۶ یا ۸ باشد.
2 اگر ۱۵ مداد را بین ۵ نفر تقسیم کنیم بر هر کدام ۳ مداد میرسد و مدادی باقی نمی ماند، بنابراین می گوییم ۱۵ بر ۵ بخش پذیر است.
3 اگر ۳۵۰ دفتر را بین ۵ نفر تقسیم کنیم به هر یک ۷۰ دفتر میرسد و دفتری باقی نمی ماند، بنابراین می گوییم عدد ۳۵۰ بر ۵ بخش پذیر است.
4 عددی بر ۵ بخش پذیر است که رقم یکان آن صفر یا ۵ باشد.
5 هر عددی که بر ۲ بخش پذیر باشد، مضرب ۲ است.
6 هر عددی که بر ۵ بخش پذیر باشد، مضرب ۵ است.
7 اگر عددی هم بر ۲ و هم بر ۵ بخش پذیر باشد آن عدد بر ۱۰ بخش پذیر است.
8 رقم یکان اعدادی که هم بر ۲ و هم بر ۵ بخش ،پذیرند یا رقم یکان اعدادی که بر ۱۰ بخش پذیرند، صفر است.
مثال
اعداد مقابل بر ۲ و ۵ بخش پذیرند.
100و 2680 و7530
باقی مانده ی تقسیم یک عدد بر ۲ یا صفر است یا ۱ اگر عدد زوج باشد باقی مانده صفر و اگر عدد فرد باشد، باقی مانده ۱ می شود.
مثال
باقی مانده ی تقسیم اعداد مقابل بر ۲ مساوی ۱ است.
۲۴۶۸۹ و ۹۷۳ و ۱۳۹۵
برای تعیین باقی مانده ی تقسیم یک عدد بر ۵، فقط کافی است که باقی مانده ی تقسیم رقم یکان آن را بر ۵ حساب کنیم.
مثال
باقی مانده ی تقسیم عدد ۱۳۵۹ را بر ۵ حساب کنید
باقی مانده ی تقسیم رقم یکان عدد، یعنی ۹ را بر ۵ حساب می کنیم.
1 عددی بر ۳ بخش پذیر است که جمع رقم هایش بر ۳ بخش پذیر باشد. برای مثال عددهای مقابل بر ۳ بخش پذیرند.
۱۲۳۰ و ۳۰۰۰۰ و ۲۷۹ و ۱۰۰۲
2 عددی بر ۹ بخش پذیر است که مجموع رقم هایش بر ۹ بخش پذیر باشد. برای مثال عددهای مقابل بر ۹ بخش پذیرند.
۱۰۰۹۸ و ۳۱۶۸۷۲ و ۷۰۲۹ و ۱۰۸
برای محاسبه ی باقی مانده ی تقسیم یک عدد بر ۳ ابتدا حاصل جمع رقم های عدد را حساب می کنیم و سپس باقی مانده ی تقسیم این حاصل جمع بر ۳ را به دست می آوریم.
مثال
باقی مانده ی تقسیم عدد ۳۲۷۶۵ را بر3 حساب کنید.
برای محاسبه ی باقی مانده ی تقسیم یک عدد بر ۹ ابتدا حاصل جمع رقمهای عدد را حساب می کنیم و سپس باقی مانده ی تقسیم حاصل جمع را بر ۹ به دست می آوریم.
مثال
باقی مانده ی تقسیم عدد ۱۳۹۵۶ را بر ۹ حساب کنید.
باقی مانده ی تقسیم هر عدد بر ۱۰ برابر است با رقم یکان عدد.
مثال
باقی مانده ی تقسیم عدد ۹۵۳۷ بر ۱۰ برابر است با ۷ و باقی مانده ی تقسیم عدد ۲۰۱۶ بر ۱۰، برابر6 است
1 عددی که هم بر ۲ و هم بر ۳ بخش پذیر باشد بر ۶ نیز بخش پذیر است. برای مثال عددهای مقابل بر ۶ بخش پذیرنده:
2010,108,1536
2 عدد که هم بر ۳ و هم بر ۵ بخش پذیر باشد بر ۱۵ نیز بخش پذیر است. مثال عددهای مقابل بر ۱۵ بخش پذیرند:
۲۱۱۳۵ و ۶۸۱۹۰ و ۲۱۰۰ و ۱۰۵
بخش پذیری بر دو
فصل 1 : عدد و الگوهای عددی
بخش پذیری بر دو
با توجه به این که هر یک از دسته های ده تایی صدتایی هزارتایی و ... را میتوان همواره به دو قسمت مساوی تقسیم کرد برای بررسی بخش پذیری هر عدد بر ۲ کافی است که یکان آن عدد بر ۲ بخش پذیر باشد؛ یعنی رقم های دهگان صدگان هزارگان و مرتبه های بالاتر تأثیری در بخش پذیری اعداد بر ۲ ندارند. نکته عددی بر ۲ بخش پذیر است که رقم یکان آن ۲۰۰، ۴، ۶ و یا ۸ باشد به عبارت دیگر، تمامی عددهای زوج بر ۲ بخش پذیر هستند.
مثال
کدام یک از عددهای مقابل بر ۲ بخش پذیر هستند؟
۲۴۶۸۰۳ و ۲۴۸۹۵۲ و ۷۲۳۴۸۱۰ و ۲۹۴۵۱ و ۳۵۷۸ و ۳۴۷
یکان عددهای ۳۵۷۸ ، ۷۲۳۴۸۱۰ و ۲۴۸۹۵۲ زوج هستند. پس این اعداد به ۲ بخش پذیرند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
بخش پذیری بر سه
فصل 1 : عدد و الگوهای عددی
بخش پذیری بر سه
در تقسیم هر بسته ی ده تایی صدتایی هزارتایی و ... بر ، همواره باقی مانده برابر یک است. بنابراین برای تعیین باقی مانده ی تقسیم عددی مانند ۴۵۳ بر ۳ با توجه به این که در این عدد ۴ دسته ی صدتایی، ۵ دسته ی ده تایی و ۳ تا یکی وجود دارد، کافی است که جمع ارقام آن را حساب کرده و بخش پذیری عدد حاصل را بر ۳ بررسی کنیم در صورتی که جمع رقمهای عدد مورد نظر بر ۳ بخش پذیر باشد آن عدد بر ۳ بخش پذیر خواهد شد.
عددی بر ۳ بخش پذیر است که جمع رقم هایش بر ۳ بخش پذیر باشد.
مثال
کدام یک از عددهای زیر بر ۳ بخش پذیر هستند؟
۲۵۸ و ۶۸۹ و ۱۴۳
کافی است که جمع رقم های هر یک از عددها را حساب کنیم عددی بر ۳ بخش پذیر است که جمع رقم های آن بر ۳ بخش پذیر باشد.
8 بر3 بخش پذیر نیست ، پس 143 بر 3 بخش پذیر نیست!
\(143 \Rightarrow 1 + 4 + 3 = 8\)
۲۳ بر ۳ بخش پذیر نیست پس ۶۸۹ بر ۳ بخش پذیر نیست!
\(689 \Rightarrow 6 + 8 + 9 = 23\)
۱۵ بر ۳ بخش پذیر است پس ۲۵۸ بر ۳ بخش پذیر میباشد.
\(258 \Rightarrow 2 + 5 + 8 = 15\)
اگر در بین ارقام ،عددی رقم صفر هم وجود داشته باشد در جمع رقم های آن عدد، نیازی به نوشتن صفر نیست چون مجموع هر عددی با صفر برابر صفر است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
بخش پذیری بر پنج و شش
فصل 1 : عدد و الگوهای عددی
بخش پذیری بر ۵
با توجه به این که هر یک از دسته های ده ،تایی صدتایی هزارتایی و ... را میتوانیم به ۵ قسمت مساوی تقسیم کنیم برای بررسی بخش پذیری هر عدد بر ۵ کافی است که یکان آن عدد صفر یا ۵ باشد و رقم های دهگان صدگان هزارگان و مرتبه های بالاتر تأثیری در بخش پذیری اعداد بر ۵ ندارند.
عددی بر ۵ بخش پذیر است که رقم یکان آن عدد ۰ یا ۵ باشد.
مثال
در بین اعداد ،زیر کدام یک بر ۵ بخش پذیر هستند؟
۱۹۲۸۳۷۴۶۵و ۳۴۹۷۶۰ و ۵۰۵۰۲ و ۹۸۰ و ۸۸۸۵ و ۵۵۵۸
رقم يكان عددهای ۸۸۸۵، ۹۸۰ ، ۳۴۹۸۶۰ و ۱۹۲۸۳۷۴۶۵ صفر یا ۵ است لذا این عددها بر ۵ بخش پذیرند.
بخش پذیری بر ۶
اعدادی مانند ۱۲، ۱۸، ۲۴ و ... که مضرب های ۶ هستند بر ۶ بخش پذیرند همان طور که ملاحظه می کنید، تمامی این عددها زوج هستند، از طرفی مجموع این عددها نیز بر ۳ بخش پذیرند، در نتیجه تمامی این عددها هم بر ۲ و هم بر ۳ بخش پذیرند.
اعدادی بر ۶ بخش پذیرند که هم بر ۲ و هم بر ۳ بخش پذیر باشند.
مثال
کدام یک از عددهای زیر بر ۶ بخش پذیر هستند؟
۳۰۴۰۵۰ و ۸۰۰۰۲۰ و ۴۵۸۹ و ۷۰۲۰ و ۴۵۰ و ۲۳۶
عدد ۲۳۶ بر ۲ بخش پذیر است اما بر ۳ بخش پذیر نیست ، پس این عدد بر ۶ بخش پذیر نمی باشد.
عدد ۴۵۰ هم بر ۲ و هم بر ۳ بخش پذیر است ، پس این عدد بر ۶ هم بخش پذیر است.
عدد ۷۰۲۰ هم بر ۲ و هم بر ۳ بخش پذیر است ، پس این عدد بر ۶ هم بخش پذیر است.
عدد ۴۵۸۹ عددی فرد است پس بر ۲ بخش پذیر نیست. در نتیجه این عدد نمیتواند بر ۶ بخش پذیر باشد.
عدد ۸۰۰۰۲۰ بر ۳ بخش پذیر نیست ، در نتیجه این عدد نمیتواند بر ۶ بخش پذیر باشد.
عدد ۳۰۴۰۵۰ هم بر ۲ و هم بر ۳ بخش پذیر است در نتیجه این عدد بر ۶ هم بخش پذیر می باشد.
بخش پذیری بر ۹
فصل 1 : عدد و الگوهای عددی
بخش پذیری بر ۹
در تقسیم هر بسته ی ده تایی صدتایی هزارتایی و ... بر عدد ،۹ همیشه باقی مانده مساوی یک می شود، بنابراین برای تعیین بخش پذیری عددی مانند ۲۰۷ بر ۹ با توجه به این که این عدد دارای دو دسته ی صدتایی و ۷ تا یکی است باید جمع رقمهای این عدد را حساب و بخش پذیری عدد حاصل را بر ۹ بررسی کنیم. نکته عددی بر ۹ بخش پذیر است که جمع رقم هایش بر ۹ بخش پذیر باشد.
مثال
کدام یک از عددهای زیر بر ۹ بخش پذیر است؟
۳۵۴۰۶ و ۲۷۴۹ و ۴۳۲
با توجه به قاعده ی بخش پذیری بر ۹ ابتدا جمع رقمهای هر یک از عددها را حساب می کنیم
\(432 \Rightarrow 4 + 3 + 2 = 9\)
بر ۹ بخش پذیر است در نتیجه ۴۳۲ بر ۹ بخش پذیر است.
\(2749 \Rightarrow 2 + 7 + 4 + 9 = 22\)
۲۲ بر ۹ بخش پذیر نیست. در نتیجه ۲۷۴۹ بر ۹ بخش پذیر نیست.
\(35406 \Rightarrow 3 + 5 + 4 + 6 = 18\)
۱۸ بر ۹ بخش پذیر است. در نتیجه ۳۵۴۰۶ بر ۹ بخش پذیر است.
هر عددی که بر ۹ بخش پذیر باشد حتما بر ۳ هم بخش پذیر است. اما بعضی از عددهایی که بر ۳ بخش پذیرند، بر ۹ بخش پذیر نیستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
بخش پذیری بر ده و پانزده
فصل 1 : عدد و الگوهای عددی
بخش پذیری بر ۱۰
هر یک از عددهای ۹۳۷۰، ۳۵۸۴۰ و ۱۲۹۳۸۰ که رقم یکان آنها صفر است هم بر ۲ و هم بر ۵ بخش پذیرند. پس این عددها بر ۵×۲ یعنی ۱۰ نیز بخش پذیرند.
1 عددی بر ۱۰ بخش پذیر است که رقم یکان آن صفر باشد.
2 اعدادی که هم بر هم بر ۵ بخش پذیرند، بر ۱۰ هم بخش پذیرند.
بخش پذیری بر ۱۵
اعدادی مانند ۱۵، ۳۰، ۴۵ ۶۰ و ... که مضرب های ۱۵ هستند بر این عدد بخش پذیرند. همان طور که ملاحظه کنید تمامی این عددها هم بر ۳ و هم بر ۵ بخش پذیر هستند.
اعدادی بر ۱۵ بخش پذیرند که هم بر ۳ و هم بر ۵ بخش پذیر باشد.
مثال
کدام یک از عددهای زیر بر ۱۵ بخش پذیرند؟
۴۳۲۵۷۶۰ و ۷۰۲۰۸۰ و ۸۹۴۶ و ۵۶۲۵ و ۲۳۴۰
عدد ۲۳۴۰ هم بر ۵ و هم بر ۳ بخش پذیر است ، در نتیجه این عدد بر ۱۵ هم بخش پذیر می باشد.
عدد ۵۶۲۵ هم بر و هم بر ۳ بخش پذیر است ، در نتیجه این عدد بر ۱۵ هم بخش پذیر می باشد.
عدد ۸۹۴۶ بر ۵ بخش پذیر نیست ، پس این عدد نمیتواند بر ۱۵ بخش پذیر باشد.
عدد ۷۰۲۰۸۰ بر ۳ بخش پذیر نیست ، پس این عدد نمیتواند بر ۱۵ بخش پذیر باشد.
عدد ۴۳۲۵۷۶۰ هم بر ۳ و هم بر ۵ بخش پذیر است ، پس این عدد بر ۱۵ هم بخش پذیر می باشد.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
معرفی اعداد صحیح
فصل 1 : عدد و الگوهای عددی
معرفی اعداد صحیح
گاهی اوقات شما با جملاتی مانند دمای هوای تهران ۴ درجه بالای صفر است یا دمای هوای اردبیل ۴ درجه زیر صفر است و همچنین ارتفاع تهران از سطح دریا ۱۱۹۰ متر بالاتر است یا ارتفاع دریای بحرالمیت از سطح دریا ۴۲۲ متر پایین تر است مواجه شده اید چه تفاوتی بین دمای بالاتر از صفر یا پایین تر از صفر وجود دارد؟
همان طور که می دانید، مفهوم ۴ درجه بالای صفر با مفهوم ۴ درجه زیر صفر متفاوت است. لذا برای نمایش تفاوت این دو عدد و همچنین ساده و مختصر کردن آنها از علامت های + یا - استفاده کنیم و طبق قرارداد می باید اعدادی که دمای بالاتر از صفر یا ارتفاع بالاتر از سطح دریا را نشان میدهند با علامت + (مثبت)، و اعدادی که دمای پایین تر از صفر و یا ارتفاع پایین تر از سطح دریا را نشان میدهند با علامت – (منفی) نمایش دهیم.
۴- = ۴ درجه زیر صفر
۴+ = ۴ درجه بالای صفر
7متر پایین تر از سطح دریا=-7
۷+ = ۷ متر بالاتر از سطح دریا
دقت داشته باشید که ارتفاع سطح دریا را مساوی صفر در نظر می گیریم.
برای تعیین علامت عددها نیاز داریم که محل مبدأ واحد اندازه گیری و جهت مثبت و منفی را قرارداد کنیم و بر اساس آن عددها را علامت دار کنیم در مثال ارتفاع از سطح دریا سطح دریا را مبدأ در نظر گرفته و ارتفاع آن را مساوی صفر در نظر می گیریم همچنین در مثال دمای هوای نیز خود صفر را به عنوان مبدأ در نظر می گیریم.
عدد صحیح
عددهای ... و ۴ و ۳ و ۲ و ۱ و ۰ و ۱ و ۲- و و ... را عددهای صحیح می نامیم.
اعداد صحیح به سه دسته ی مهم تقسیم می شوند:
۱ اعداد صحیح مثبت که شامل عددهای ۱ و ۲ و ۳+و 4+ و ... می باشند.
۲ عدد صفر که نه مثبت است و نه منفی.
3اعداد صحیح منفی که شامل عددهای 1- و 2- و3- و ۴- و ... می باشند.
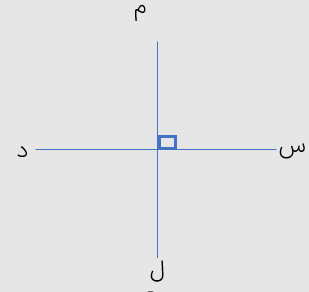
محور اعداد صحیح
در ریاضی برای یکی شدن قراردادها و همچنین نمایش عددها روی محور اعداد سمت راست صفر را روی محور مثبت و سمت چپ صفر را منفی در نظر می گیریم.
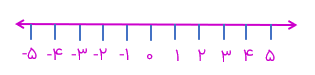
محور اعداد زیر را در نظر بگیرید. نقطه ی مبدأ این محور را با عدد صفر نشان میدهیم. عددهای سمت راست صفر را عددهای صحیح مثبت و عددهای سمت چپ صفر را عددهای صحیح منفی می
نامیم.
1 بزرگ ترین عدد صحیح ،منفی عدد -۱ و کوچک ترین عدد صحیح منفی وجود ندارد.
2 کوچک ترین عدد صحیح ،مثبت عدد ۱ و بزرگترین عدد صحیح مثبت وجود ندارد.)مشخص نیست).
3 علامت هر عدد را در سمت چپ آن قرار میدهیم؛ مانند عدد +7یا ۵- .
7+ را می خوانیم مثبت ۷ و ۵ - را می خوانیم منفی ۵ .
4 در نمایش عددهای مثبت میتوانیم علامت مثبت را ننویسیم، یعنی ۵ = ۵+است.
مقایسه ی عددهای صحیح
بر روی محور اعداد صحیح هر چه به سمت راست یعنی به سمت مثبتها پیش برویم عددها : بزرگ تر می شوند و هر چه به سمت چپ (یعنی به سمت منفی(ها پیش برویم عددها کوچک تر میشوند. بنابراین عدد ۳- از عدد ۵- بزرگ تر است. (۵<۳-) و یا عدد ۱+ از عدد ۱۰۰۰- بزرگ تر است (۱+< ۱۰۰۰-).
پس عددهای صحیح سه دسته هستند: عددهای صحیح مثبت که از صفر بزرگ تر هستند، عددهای صحیح منفی که از صفر کوچک تر هستند و عدد صفر که نه مثبت است و نه منفی.
اعداد صحیح مثبت > صفر > اعداد صحیح منفی
روی محور هر چه در جهت مثبت پیش برویم عددهای بزرگ تر میشوند و هر چه به سمت چپ یعنی در جهت منفی پیش برویم عددها کوچک تر می شوند؛ یعنی:
۱+ 0 <و ۰ > ۴ -و ۲-< ۵۳-
قرینه ی اعداد صحیح
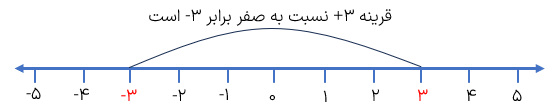
در سال گذشته با مفهوم قرینه نسبت به یک نقطه آشنا شدید در محور زیر اگر بخواهیم قرینه ی عدد ۳+ را نسبت به مبدأ که همان نقطه ی صفر است مشخص کنیم عدد ۳- به دست می آید.
همان طور که ملاحظه می کنید برای قرینه کردن هر عددی نسبت به صفر (مبدأ)، کافی است که علامت آن را تغییر دهیم یعنی علامت مثبت را به منفی و علامت منفی را به مثبت تبدیل کنیم.
اگر عددی علامت نداشته باشد علامت آن مثبت در نظر گرفته میشود یا میتوانیم برای عددهای مثبت، علامت آنها را قرار ندهیم؛ یعنی ۱۷+ = ۱۷ و ۶ = ۶+
فاصله ی عدد ۲+ تا صفر با فاصله ی عدد 2-تا صفر برابر است؛ به همین دلیل عدد 2- را قرینه ی عدد ۲ می گوییم و به همین ترتیب قرینه ی عدد ۱۱ عدد -۱۱ و قرینه ی عدد ۹۳-، عدد ۹۳ است.
1 قرینه ی صفر، خود صفر است.
2 علامت قرینه در ریاضی( _ ) است.
مثال
قرینه 4+ و 9+ را بدست اورید.
4-=(4+)-=قرینه ی4+
-9=قرینه ی+9
هر عددی را که قرینه کنیم علامت آن تغییر می کند.
قرینه ی قرینه ی هر عدد برابر است با خود عدد:
قرینه ی قرینه 5-=\(( - ( - ( - 5))) = - 5\)
قرینه ی قرینه 3+=\( - ( - ( + 3)) = + 3\)
کسرها
فصل 2 : کسر
مفهوم کسر
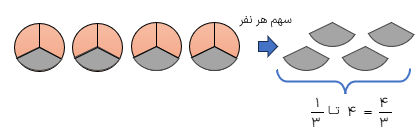
به جزئی یا قسمتی از یک واحد ،کامل کسری از آن واحد گفته میشود بنابراین کسری از کل یعنی جزئی یا قسمتی از آن کل
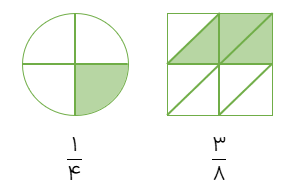
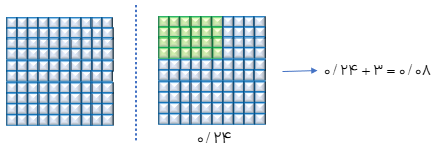
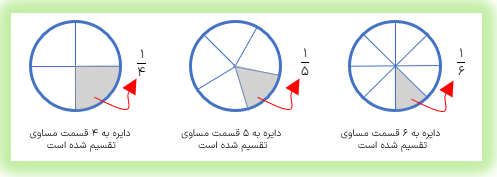
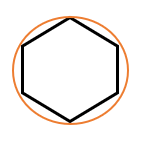
در شکل مقابل \(\frac{1}{4}\) دایره و \(\frac{3}{8}\)مربع رنگ شده است.
\(\frac{1}{4}\)یعنی یک قسمت از ۴ قسمت مساوی.
\(\frac{3}{8}\)یعنی سه قسمت از ۸ قسمت مساوی.
عدد مخلوط
اگر صورت کسر بزرگ تر از واحدی بر مخرجش بخش پذیر نباشد آن کسر را میتوان به صورت عدد مخلوط (ترکیبی از عدد صحیح و کسر) نوشت.
مثال
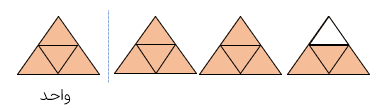
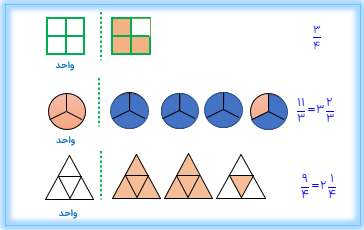
عدد مخلوط ۲۳ را به وسیله ی شکل نمایش دهید.
عدد مخلوط ۲۲ با کسر\(\frac{{11}}{4}\)برابر است.
شکل درست یک عدد مخلوط این است که حتما کسر نوشته شده در عدد مخلوط کوچک تر از واحد باشد.
مثال
شکل درست عدد مخلوط \(3\frac{5}{2}\) را بنویسید.
\(\frac{5}{2} = 2\frac{1}{2} \to 3\frac{5}{2} = 3 + 2\frac{1}{2} = 5\frac{1}{2}\)
کسرهای مساوی
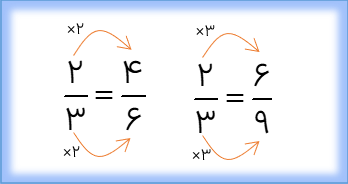
اگر صورت و مخرج کسری را در عدد طبیعی بزرگ تر از ۱ ضرب و یا بر عدد. ر عدد طبیعی بزرگ تر از یک تقسیم کنیم، کسری مساوی کسر اولیه به دست می آید.
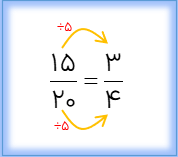
کسر\(\frac{3}{4}\)با \(\frac{{15}}{{20}}\) کسر مساوی است.
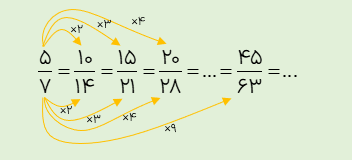
برای هر کسر، بی شمار کسر مساوی می توان نوشت:
\(\frac{{{3_{ \times 2}}}}{{{4_{ \times 2}}}} = \frac{6}{8} = \frac{9}{{12}} = \frac{{12}}{{16}} = \frac{{15}}{{20}} = \frac{{18}}{{24}} = \frac{{21}}{{28}} = ...\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مخرج مشترک
فصل 2 : کسر
کوچک ترین مخرج مشترک دو یا چند کسر
اگر دو یا چند کسر داشته باشیم و بزرگترین مخرج این ،کسرها بر بقیه ی مخرجها بخش پذیر باشد، همان مخرج بزرگتر کوچک ترین مخرج مشترک کسرها می شود.
مثال
کوچک ترین مخرج مشترک کسرهای\(\frac{1}{2},\frac{5}{6},\frac{6}{7},\frac{3}{{14}},\frac{{11}}{{21}},\frac{5}{{42}}\) را بیابید.
چون ۴۲ بر تمامی مخرج ها بخش پذیر است پس کوچک ترین مخرج مشترک این کسرها، عدد ۴۲ است.
اگر مخرج بزرگ تر بر بقیه ی مخرجها بخش پذیر نبود میتوان با نوشتن کسرهای مساوی برای دو یا چند کسر داده شده، کوچک ترین مخرج مشترک آن ها را بیابیم.
مثال
کوچک ترین مخرج مشترک دو کسر \(\frac{5}{6},\frac{3}{4}\) را بنویسید.
\(\begin{array}{l}\frac{3}{4} = \frac{6}{8} = \frac{9}{{12}} = \frac{{12}}{{16}}\\\\\frac{5}{6} = \frac{{10}}{{12}} = \frac{{15}}{{18}}\end{array}\)
همان طور که میبینید عدد ۱۲ کوچک ترین مخرج مشترک دو کسر است.
روش بهتر برای یافتن کوچک ترین مخرج مشترک دو کسر این است که اگر بزرگ ترین مخرج بر دیگر مخرج ها بخش پذیر نبود آن را در عددهای ۲ ,۳ .۴, ۵ و ... به ترتیب ضرب کنیم تا جایی که بر مخرج یا مخرج های دیگر بخش پذیر شود.
مثال
کوچک ترین مخرج مشترک دو کسر\(\frac{4}{{15}},\frac{3}{{10}}\) را بیابید.
عدد ۳۰ بر ۱۰ بخش پذیر است، پس کوچک ترین مخرج مشترک\(\frac{4}{{15}},\frac{3}{{10}}\) عدد ۳۰ است.
۱۵×۲ = ۳۰
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
مقایسه ی کسرها
فصل 2 : کسر
مقایسه ی کسرها
مثال
الف اگر دو کسر دارای مخرجهای مساوی باشند کسری بزرگ تر است که صورتش بزرگ تر باشد.
\(\begin{array}{l}\frac{5}{7} > \frac{2}{7}\\\\\frac{3}{{11}} < \frac{9}{{11}}\end{array}\)
ب اگر دو کسر دارای صورت های مساوی باشند کسری بزرگ تر است که مخرجش کوچک تر باشد.
\(\begin{array}{l}\frac{3}{4} > \frac{3}{5}\\\\\frac{9}{5} < \frac{9}{2}\end{array}\)
ج اگر دو کسر، نه صورتهای برابر و نه مخرجهای برابر داشته باشند ابتدا دو کسر را هم مخرج و یا هم صورت میکنیم و سپس آنها را مقایسه می کنیم
مثال
برای مقایسه ی دو کسر که صورتهای آنها برابر نباشند و مخرجهای آنها نیز برابر نباشند، از روش ساده تری به نام روش ضرب دری یا طرفین وسطین می توان استفاده کرد.
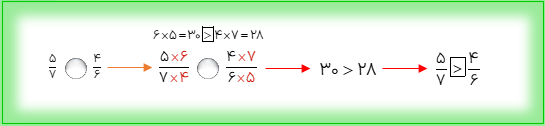
مقایسه ی کسرها توسط محور
در این روش دو محور رسم میکنیم که دقیقا واحدهای هم اندازه داشته باشند و صفرهای دو محور دقیقا زیر هم قرار گیرند.
مثال
کسرهای \(\frac{2}{3},\frac{3}{4}\) را روی محور مقایسه کنید.
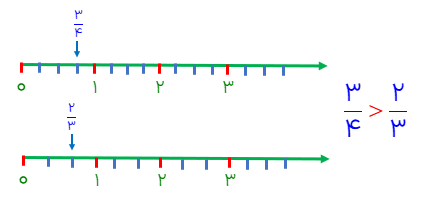
مقایسه ی دو کسر با شکل
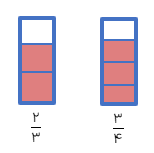
در این روش دو واحد برابر انتخاب میکنیم و سپس با توجه به مخرج کسرها آنها را به قسمت های مساوی تقسیم کرده و سپس کسرها را روی شکل مشخص و مقایسه می کنیم
مثال
کسرهای \(\frac{2}{3},\frac{3}{4}\) را با شکل مقایسه کنید.
طبق شکل مقابل: \(\frac{2}{3} < \frac{3}{4}\)
جمع و تفریق کسرها
فصل 2 : کسر
جمع و تفریق کسرها
به طور کلی در جمع و تفریق ،کسرها باید مخرجها مساوی باشند و اگر مخرجها مساوی نبودند، با استفاده از کوچک ترین مخرج مشترک آنها مخرجهایشان را مساوی می کنیم.
مثال
حاصل جمع و تفریق های زیر را حساب کنید.
الف \(\frac{2}{{13}} + \frac{4}{{13}}\)
\(\frac{2}{{13}} + \frac{4}{{13}} = \frac{{2 + 4}}{{13}} = \frac{6}{{13}}\)
ب \(\frac{4}{9} + \frac{2}{9}\)
\(\frac{4}{9} + \frac{2}{9} = \frac{{4 + 2}}{9} = \frac{6}{9}\)
مثال
حاصل عبارت زیر را حساب کنید و به ساده ترین صورت بنویسید.
\(\frac{2}{3} + \frac{1}{4} + \frac{5}{{12}}\)
\(\frac{2}{3} + \frac{1}{4} + \frac{5}{{12}} = \frac{8}{{12}} + \frac{3}{{12}} + \frac{5}{{12}} = \frac{{16}}{{12}} = \frac{4}{3} = 1\frac{1}{3}\)
جمع اعداد مخلوط
برای جمع اعداد مخلوط بهتر است عددهای صحیح را با هم و کسرها را نیز با هم جمع کنیم.
مثال
حاصل عبارت مقابل را حساب کنید.
\(2\frac{2}{5} + 3\frac{1}{3}\)
\(2\frac{2}{5} + 3\frac{1}{3} = (2 + 5) + (\frac{2}{5} + \frac{1}{3}) = 5 + \frac{6}{{15}} + \frac{5}{{15}} = 5\frac{{11}}{{15}}\)
تفریق اعداد مخلوط
مانند جمع اعداد مخلوط بهتر است که در تفریق ،هم عددهای صحیح را از هم کم کنیم و کسرها را نیز از هم تفریق کنیم.
مثال
حاصل عبارت زیر را حساب کنید.
\(5\frac{3}{4} - 2\frac{2}{3}\)
\(5\frac{3}{4} - 2\frac{2}{3} = (5 - 2) + (\frac{3}{4} - \frac{2}{3})3 + \frac{9}{{12}} - \frac{8}{{12}} = 3\frac{1}{{12}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
کسر های مساوی
فصل 2 : کسر
کسر های مساوی
با مفهوم کسر در سال های گذشته آشنا شدید و آموختید که هرگاه جزئی از یک واحد مورد نظر باشد، آن را با کسر نشان میدهیم به مثال های زیر دقت کنید.
کسری که صورت آن بر مخرجش بخش پذیر باشد با یک عدد صحیح برابر است.
کسرهای مساوی
اگر صورت و مخرج کسری را در عددی طبیعی ضرب کنیم کسری مساوی با آن به دست می آید. به این ترتیب میتوانیم بی شمار کسر مساوی با یک کسر بنویسیم.
جمع و تفریق عددهای کسری
برای انجام جمع و تفریق بین دو یا چند کسر ابتدا باید آنها را با استفاده از یکی از روش های زیر هم مخرج کنیم، بعد از هم مخرج کردن ،کسرها یکی از مخرجها را می نویسیم و صورت کسرها را با توجه به علامت بین کسرها با هم جمع یا از هم کم می.کنیم دقت داشته باشید که گاهی اوقات یکی از مخرج ها بر دیگری بخش پذیر است، در این صورت به سادگی هر دو کسر هم مخرج می شوند.
هم مخرج کردن کسرها با استفاده از نوشتن کسرهای مساوی
در این روش از هم مخرج کردن دو ،کسر باید کسرهای مساوی با هر یک از کسرها را بنویسیم، تا جایی که به کسرهای هم مخرج برسیم.
مثال
به مثال های زیر توجه کنید.
\(\begin{array}{l}\frac{{{5_{ \times 3}}}}{{{4_{ \times 3}}}} + \frac{{{1_{ \times 2}}}}{{{6_{ \times 2}}}} = \frac{{15}}{{12}} + \frac{2}{{12}} = \frac{{15 + 2}}{{12}} = \frac{{17}}{{12}}\\\\\frac{{{5_{ \times 6}}}}{{{4_{ \times 6}}}} + \frac{{{1_{ \times 4}}}}{{{6_{ \times 4}}}} = \frac{{30}}{{24}} + \frac{4}{{24}} = \frac{{34}}{{24}} = \frac{{17}}{{12}}\end{array}\)
اگر نوشتن کسرهای مساوی را ادامه دهیم به کسرهای هم مخرج \(\frac{4}{{24}},\frac{{30}}{{24}}\) می رسیم که با جمع این دو کسر و ساده کردن جواب جمع مجددا به همان جواب قبلی می رسیم.
در مثال بالا، عددهای ۱۲ و ۲۴ مخرج های مشترک دو کسر و هستند ولی به عدد ۱۲، کوچک ترین مخرج مشترک دو کسر هم گفته میشود که استفاده از این عدد باعث ساده تر شدن محاسبات می گردد.
بنابراین برای انجام جمع و تفریق دو کسر با مخرجهای ،نابرابر بهتر است ابتدا کوچک ترین مخرج مشترک دو کسر را بیابیم، سپس جمع یا تفریق را انجام دهیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
کوچک ترین مضرب مشترک
فصل 2 : کسر
نوشتن مضرب های هر یک از مخرج ها
در این روش ابتدا مضرب های هر یک از مخرجها را مینویسیم اولین مضرب مشترک بین آن ها، همان کوچک ترین مخرج مشترک کسرها خواهد شد.
مثال
جمع زیر را انجام دهید.
الف)\(\frac{5}{9} + \frac{7}{6}\)
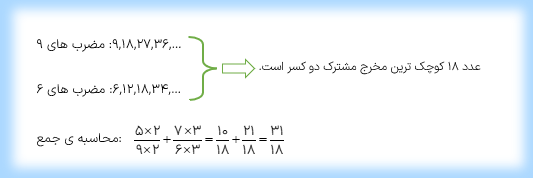
جمع و تفریق عددهای مخلوط
برای انجام جمع یا تفریق دو عدد ،مخلوط ابتدا قسمت صحیح هر دو عدد را با توجه به علامت بین عددها، با هم جمع یا تفریق میکنیم . سپس قسمت های کسری را پس از هم مخرج کردن با توجه به علامت عددها با هم جمع یا از هم کم میکنیم.
مثال
تفریق زیر را انجام دهید.
\(3\frac{1}{{24}} - 2\frac{3}{{16}}\)
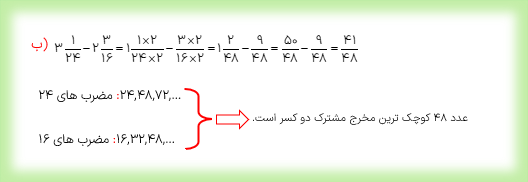
همان طور که ملاحظه نمودید گاهی اوقات در تفریق دو عدد مخلوط بعد از تفریق قسمت صحیح آن ها، قسمت کسری اولین عدد از قسمت کسری دومین عدد کوچک تر میشود و به این ترتیب تفریق امکان پذیر نمی باشد. در چنین مواقعی یک از روش های تفریق این است که مانند مثال بالا عدد مخلوط را به کسر تبدیل کنیم، سپس عملیات تفریق را انجام دهیم.
ضرب کسرها
فصل 2 : کسر
ضرب کسرها
در ضرب دو یا چند کسر باید صورتها را در هم ضرب کنیم و در صورت کسر حاصل ضرب قرار دهیم و مخرج ها را نیز در هم ضرب کنیم و در مخرج کسر حاصل ضرب قرار دهیم.
مثال
حاصل ضرب زیر را حساب کنید.
الف \(\frac{4}{7} \times \frac{5}{{11}}\)
\(\frac{4}{7} \times \frac{5}{{11}} = \frac{{4 \times 5}}{{7 \times 11}} = \frac{{20}}{{77}}\)
ب\(\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7}\)
\(\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7} = \frac{{2 \times 4 \times 6}}{{3 \times 5 \times 7}} = \frac{{48}}{{105}}\)
در ضرب ،کسرها اگر بتوانیم صورت کسرها را با مخرج آنها ساده کنیم بهتر است که ابتدا این کار را انجام دهیم و سپس حاصل ضرب را حساب کنیم این کار سرعت و دقت محاسبه را افزایش می دهد و نیازی به ساده کردن کسر حاصل نیز نمی باشد.
مثال
حاصل ضرب زیر را حساب کنید.
\(\frac{{12}}{{15}} \times \frac{{25}}{{18}}\)
\(\frac{{12}}{{15}} \times \frac{{25}}{{18}} = \frac{2}{3} \times \frac{5}{3} = \frac{{2 \times 5}}{{3 \times 3}} = \frac{{10}}{9} = 1\frac{1}{9}\)
ضرب عددهای مخلوط
برای ضرب اعداد مخلوط از راه محاسبه ابتدا اعداد مخلوط را به کسر تبدیل میکنیم و سپس کسرها را در هم ضرب می کنیم و حاصل را به دست می آوریم.
مثال
حاصل ضرب زیر را بدست اورید.
\(3\frac{3}{5} \times 2\frac{2}{9}\)
\(3\frac{3}{5} \times 2\frac{2}{9} = \frac{{18}}{5} \times \frac{{20}}{9} = \frac{8}{1} = 8\)
هرگاه حاصل ضرب دو عدد مساوی ۱ ،باشد آن دو عدد را معکوس یکدیگر می.گویند. همه ی عددها به جز صفر، معکوس دارند.
برای مشخص کردن معکوس یک کسر، باید جای صورت و مخرج آن را عوض کنیم.
اگر بخواهیم معکوس یک عدد مخلوط را مشخص کنیم ابتدا باید آن را به شکل کسر در آوریم و سپس کسر را معکوس کنیم.
مثال
معکوس عدد \(3\frac{1}{4}\) را بنویسید.
\(3\frac{1}{4} = \frac{{13}}{4} \to \frac{4}{{13}}\)
مثال
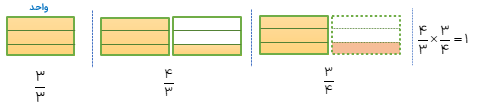
با استفاده از شکل تساوی های زیر را کامل کنید.
\(\frac{3}{4} \times \frac{4}{3}\)
نصف یک عدد یعنی آن عدد ضرب در\(\frac{1}{2}\)
مثال
نصف\(\frac{5}{6}\)یعنی:
\(\frac{5}{6} \times \frac{1}{2} = \frac{5}{{12}}\)
ربع یک عدد یعنی آن عدد ضرب در \(\frac{1}{4}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
روش های محاسبه ضرب کسرها
فصل 2 : کسر
روش های محاسبه ضرب کسرها
یادآوری
در سال قبل با سه روش محاسبه ی ضرب کسرها آشنا شدید که عبارت اند از:
۱ رسم شکل
۲ رسم محور
۳ محاسبات ریاضی
با توجه به این که روش محاسباتی سریع ترین و ساده ترین روش نسبت به دو روش دیگر است، لذا در سال ششم بیش تر از این روش استفاده می کنیم در این روش برای محاسبه ی حاصل ضرب دو ،کسر، ابتدا صورت های دو کسر را در همدیگر و مخرجهای دو کسر را نیز در همدیگر ضرب میکنیم و به عنوان صورت و مخرج جدید می نویسیم. بهتر است قبل از انجام ،ضرب صورت ها را با مخرج ها ساده کنیم دقت داشته باشید که در ضرب کسرها، نیازی به هم مخرج کردن کسرها نیست.
مثال
حاصل عبارت زیر رابدستت اورید.
الف\(\frac{8}{{21}} \times \frac{{14}}{{40}}\)
\(\frac{8}{{21}} \times \frac{{14}}{{40}} = \frac{{8 \times 14}}{{21 \times 40}} = \frac{2}{{15}}\)
عددهای ۸ و ۴۰ را به ۸ ساده کردیم و عددهای ۱۴ و ۲۱ را نیز به ۷ ساده کردیم و در آخر ساده شده ی عددها را در یک دیگر ضرب کردیم.
ب\(\frac{{27}}{{36}} \times \frac{{28}}{{21}}\)
\(\frac{{27}}{{36}} \times \frac{{28}}{{21}} = \frac{{27 \times 28}}{{36 \times 21}} = \frac{1}{1} = 1\)
در ابتدا عددهای ۲۷ و ۳۶ را به ۹ و عددهای ۲۸ و ۲۱ را نیز به ۷ ساده میکنیم و این عمل را مجددا برای ساده شده ی عددها تکرار می کنیم
ضرب عددهای مخلوط
برای انجام ضرب عددهای مخلوط ابتدا باید آنها را به عدد کسری تبدیل سپس مثل ضرب كسرها عمل کنیم.
مثال
عبارت زیر را حل کنید.
\(2\frac{3}{7} \times 2\frac{5}{8}\)
\(2\frac{3}{7} \times 2\frac{5}{8} = \frac{{24}}{7} \times \frac{{21}}{8} = \frac{{24 \times 21}}{{7 \times 8}} = \frac{9}{1} = 9\)
معکوس یک کسر
اگر جای صورت و مخرج یک کسر را تغییر دهیم معکوس آن کسر به دست می آید.
\(\frac{3}{5} \to \frac{5}{3}\,\,\,\,\,\,\,\,\,\,\,\,\frac{7}{2} \to \frac{2}{7}\,\,\,\,\,\,\,\,\,\,\,\,\frac{4}{3} \to \frac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,5 = \frac{5}{1} \to \frac{1}{5}\)
۱ همه ی اعداد به غیر از صفر معکوس دارند.
۲ برای تعیین معکوس یک عدد ،مخلوط ابتدا باید آن عدد را به کسر تبدیل، و سپس معکوس کنیم.
3 هرگاه حاصل ضرب دو عدد برابر یک شود آن دو عدد معکوس یک دیگر هستند. به عبارت دیگر، حاصل ضرب هر عددی در معکوسش همیشه مساوی یک می شود.
\(\frac{3}{5} \times \frac{5}{3} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\frac{1}{3} \times \frac{3}{7} = \frac{7}{3} \times \frac{3}{7} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,5 \times \frac{1}{5} = 1\)
مثال
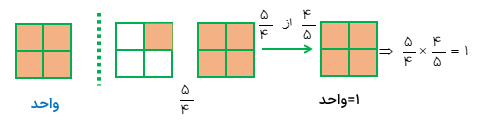
با رسم شکل نشان دهید که \(\frac{5}{4},\frac{4}{5}\) معکوس یک دیگر هستند.
کافی است که نشان دهیم حاصل ضرب این دو کسر برابر یک است. در ابتدا شکل \(\frac{5}{4}\)را رسم می کنیم، حالا برای مشخص کردن\(\frac{5}{4}\) از \(\frac{4}{5}\) باید ۴ خانه ی رنگ شده از شکل\(\frac{5}{4}\) را انتخاب کنیم. به این ترتیب ملاحظه می کنید که حاصل برابر یک واحد شد.
پس این دو کسر طبق نکته بالا معکوس یکدیگرند.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
پیدا کردن مقدار نامعلوم در تساوی ها
فصل 2 : کسر
پیدا کردن مقدار نامعلوم در تساوی ها
مثال
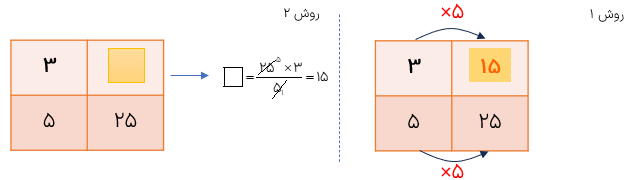
در تساوی \(\frac{3}{5} = \frac{{15}}{?}\) به جای علامت سؤال چه عددی باید نوشت؟
همان طور که ملاحظه میکنید عدد ۳ پنج برابر شده است پس باید ۵ هم پنج برابر شود.
\(\frac{{{3_{ \times 5}}}}{5} = \frac{{15}}{?}\)
به عبارت دیگر، اول ۱۵ را بر ۳ تقسیم میکنیم تا بفهمیم که ۳ چند برابر شده است و سپس ۵ را هم در همان عدد ضرب میکنیم .
برای حل این گونه سؤالات به روش زیر عمل می کنیم:
\(\frac{3}{5} = \frac{{15}}{?} \to ? = 5 \times \frac{{15}}{3} = \frac{{5 \times 15}}{3} = 25\)
در زنگ ورزش یک کلاس ۳۰ نفری،\(\frac{2}{5}\) از دانش آموزان فوتبال،\(\frac{1}{2}\) والیبال و بقیه ی آن ها تنیس روی میز بازی میکنند.
الف چند نفر فوتبال بازی می کنند؟
۱۲ نفر فوتبال بازی میکنند
\(\frac{2}{5} \times 30 = \frac{{2 \times 30}}{5} = 12\)
ب چند نفر والیبال بازی می کنند؟
۱۰ نفر والیبال بازی میکنند
\(\frac{1}{3} \times 30 = \frac{{1 \times 30}}{3} = 10\)
ج چند نفر تنیس روی میز بازی می کنند؟
۸ نفر تنیس روی میز بازی میکنند
\(30 - (10 = 12) = 30 - 22 = 8\)
تقسیم کسرها
فصل 2 : کسر
تقسیم کسرها
برای محاسبه ی تقسیم کسرها از راه محاسبه یک روش کلی وجود دارد به این ترتیب که کسر اول را می نویسیم، عمل تقسیم را به ضرب تبدیل میکنیم و کسر دوم را معکوس میکنیم (یعنی جای صورت و مخرج را عوض می کنیم و سپس مانند ضرب کسرها، حاصل را به دست می آوریم.)
مثال
به عبارت زیر توجه کنید.
\(\frac{4}{5} \div \frac{2}{7} = \frac{4}{5} \times \frac{7}{2} = \frac{{14}}{5} = 2\frac{4}{5}\)
اگر در تقسیم ،کسرها صورت کسر سمت چپ بر صورت کسر سمت راست بخش پذیر باشد و مخرج کسر سمت چپ بر مخرج کسر سمت راست بخش پذیر باشد میتوانیم آنها را بر هم تقسیم کنیم و به سادگی جواب را به دست آوریم.
تقسیم کسرها به کمک شکل
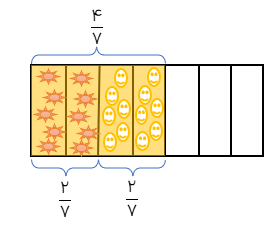
می خواهیم حاصل \(\frac{4}{7} \div \frac{2}{7}\) را به کمک شکل محاسبه کنیم.
ابتدا یک مستطیل را به عنوان واحد رسم میکنیم و آن را به ۷ قسمت مساوی تقسیم می کنیم ابتدا یک مستطیل را به عنوان واحد رسم میکنیم و ۴ قسمت آن را رنگ میکنیم اکنون هر دو قسمت آن را با رنگ های متفاوت مشخص می کنیم. دو تا\(\frac{2}{7}\)روی شکل مشخص میشود پس حاصل می شود ۲؛ یعنی :\(\frac{4}{7} \div \frac{2}{7} = 2\)
تقسیم کسرها به کمک محور اعداد
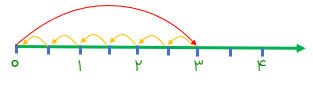
می خواهیم حاصل \(3 \div \frac{1}{2}\) را به کمک محور حساب کنیم ابتدا محور را رسم می کنیم و ۳ واحد را روی آن مشخص می کنیم چون مخرج کسر ۲ است هر واحد را به ۲ قسمت تقسیم میکنیم اکنون باید ببینیم که در ۳ واحد، چندتا\(\frac{1}{2}\)هست.
همان طور که روی محور می بینیم در ۳ واحد، ۶ تا\(\frac{1}{2}\)داریم، پس :\(3 \div \frac{1}{2} = 6\)
برای تقسیم اعداد مخلوط ابتدا باید آنها را به کسر تبدیل کنیم و سپس عمل تقسیم را انجام دهیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
روش محاسبه در تقسیم کسرها
فصل 2 : کسر
روش محاسبه در تقسیم کسرها
اگر بخواهیم چهار کلوچه را بین سه نفر تقسیم کنیم میتوانیم در ابتدا هر کلوچه را به سه قسمت تقسیم کنیم و سپس به هر نفر ۴ تا\(\frac{1}{3}\) کلوچه بدهیم؛ به این ترتیب سهم هر نفر\(\frac{4}{3}\)کلوچه می شود.
به عبارت دیگر:
\(4 \div 3 = 4 \times \frac{1}{3} = \frac{4}{3}\)
با توجه به عبارت بالا برای تقسیم دو عدد صحیح برهم کافی است که اولین عدد را در معکوس دومین عدد ضرب کنیم، سپس حاصل ضرب را به دست آوریم.
مثال
حاصل هر یک از تقسیم های زیر را به دست آورید.
\(7 \div 4\)الف
\(7 \div 4 = 7 \times \frac{1}{4} = 7\)
ب \(20 \div 9\)
\(20 \div 9 = 20 \times \frac{1}{9} = \frac{{20}}{9}\)
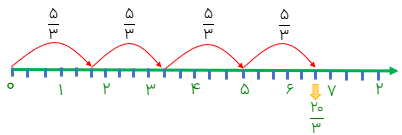
در محور بالا در\(\frac{{20}}{3}\) چهار تا\(\frac{5}{3}\)قرار دارد. به عبارت دیگر:
\(\frac{{20}}{3} \div \frac{5}{3} = \frac{{20}}{5} = 4\)
با توجه به عبارت بالا برای تقسیم دو کسر با مخرج های برابر کافی است که صورت اولین کسر را بر صورت دومین کسر تقسیم کنیم.
برای تقسیم دو عدد مخلوط بر یک دیگر ابتدا آنها را به صورت کسری می نویسیم، سپس حاصل تقسیم را به دست می آوریم.
اگر دو کسر هم مخرج ،باشند حاصل تقسیم آنها به سادگی قابل محاسبه است. پس از این خاصیت می توانیم برای تقسیم کسرهایی که مخرج آنها برابر نمی باشد هم استفاده کنیم به این ترتیب که ابتدا دو کسر را هم مخرج کنیم و سپس به روش بالا عمل کنیم.
مثال
حاصل تقسیم های زیر را به دست آورید.
الف \(\frac{9}{{14}} \div \frac{1}{2}\)
\(\frac{9}{{14}} \div \frac{{{1_{ \times 7 = 7}}}}{{{2_{ \times 7 = 14}}}} = \frac{9}{{14}} \times \frac{7}{{14}} = \frac{9}{7}\)
\(2\frac{1}{7} \div 3\frac{1}{2}\) ب
\(2\frac{1}{7} \div 3\frac{1}{2} = \frac{{15}}{7} \div \frac{7}{2} = \frac{{30}}{{14}} \div \frac{{49}}{{14}} = \frac{{30}}{{49}}\)
روش کلی محاسبه ی حاصل تقسیم دو عدد
کافی است که اولین عدد را در معکوس دومین عدد ضرب کنیم و حاصل ضرب را پس از ساده کردن صورت ها با مخرج ها به دست آوریم
مثال
حاصل عبارت زیر را بدست اورید.
الف\(\frac{9}{4} \div \frac{1}{2}\)
\(\frac{9}{4} \div \frac{1}{2} = \frac{9}{4} \times \frac{2}{1} = \frac{{9 \times 2}}{{4 \times 1}} = \frac{9}{7}\)
ب\(\frac{{20}}{9} + \frac{5}{6}\)
\(\frac{{20}}{9} + \frac{5}{6} = \frac{{20}}{9} \times \frac{6}{5} = \frac{8}{3}\)
حاصل عبارت \(\left( {2\frac{1}{8} - 1\frac{5}{6}} \right) \div 2\frac{5}{{12}}\)را به دست آورید.
ابتدا حاصل عبارت داخل پرانتز را به دست میآوریم سپس جواب آن را بر عدد مخلوط تقسیم می کنیم.
عبارت داخل پانتز=\(2\frac{1}{8} - 1\frac{5}{6} = 1\frac{1}{8} - \frac{5}{6} = 1\frac{3}{{24}} - \frac{{20}}{{24}} = \frac{{27}}{{24}} - \frac{{20}}{{24}} = \frac{7}{{24}}\)
\(\left( {2\frac{1}{8} - 1\frac{5}{6}} \right) \div 2\frac{5}{{12}} = \frac{7}{{24}} \div \frac{{29}}{{12}} = \frac{7}{{24}} \times \frac{{12}}{{29}} = \frac{7}{{58}}\)
\(\frac{3}{5}\)گنجایش ظرفی ۷۵ لیتر است. گنجایش باقی مانده ی ظرف چه قدر است؟
گنجایش باقی مانده ی ظرف \( \ 125 - 75 = 50\)
گنجایش کل ظرف \(75 \div \frac{3}{5} = \frac{{75}}{1} \times \frac{5}{3} = 125\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
محاسبات با کسر
فصل 2 : کسر
محاسبات با کسر
برای محاسبه ی حاصل کسرهایی که صورت و مخرج آن ها دارای عملیات ریاضی است، مانند مثال زیر عمل می کنیم:
مثال
حاصل عبارت مقابل را حساب کنید.
\(\frac{{\frac{2}{3} - \frac{1}{4}}}{{\frac{1}{2} + \frac{1}{3}}}\)
\(\frac{{\frac{2}{3} - \frac{1}{4}}}{{\frac{1}{2} + \frac{1}{3}}} = \frac{{\frac{8}{{12}} - \frac{3}{{12}}}}{{\frac{3}{6} + \frac{2}{6}}} = \frac{{\frac{5}{{12}}}}{{\frac{5}{6}}} = \frac{5}{{12}} \div \frac{5}{6} = \frac{1}{2}\)
مثال
یک ویروس رایانه حافظه ی رایانه ای را پاک کند. این ویروس روز اول \(\frac{2}{8}\)حافظه و روز دوم \(\frac{2}{8}\)حافظه ی باقی مانده از روز اول و روز سوم \(\frac{3}{8}\)باقی مانده از روزهای قبل را پاک می کند. حساب کنید پس از ۳ روز هنوز چه کسری از حافظه پاک نشده است؟
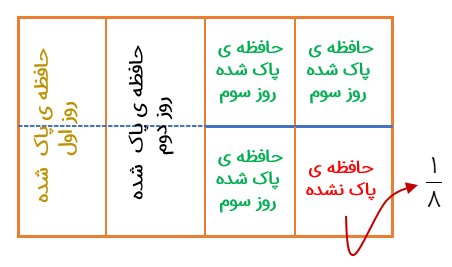
هنوز\(\frac{1}{8}\)حافظه پاک نشده است.
در انجام عملیات ریاضی باید به ترتیب و اولویت عملیات داده شده دقت کنیم به طور کلی در یک عبارت محاسباتی باید به ترتیب زیر عمل کنیم.
۱ محاسبه ی پرانتز ها از داخلی ترین آنها
۲ انجام ضرب یا تقسیم هر کدام که از چپ به راست عبارت، زودتر دیده شد.
3 انجام جمع یا ،تفریق هر کدام که از چپ به راست عبارت، زودتر دیده شد.
مثال
حاصل عبارت زیر را بدست اورید.
الف\(\left( {3\frac{3}{5} - 2\frac{{11}}{5}} \right) \div 1\frac{3}{{10}}\)
در ابتدا، حاصل عبارت داخل پرانتز را حساب کرده و عدد به دست آمده را بر\(1\frac{3}{{10}}\) تقسیم می کنیم.
محاسبه ی داخل پرانتز:\(3\frac{3}{5} - 2\frac{{11}}{5} = 1\frac{3}{5} - \frac{{11}}{{15}} = 1\frac{9}{5} - \frac{{11}}{{15}} = \frac{{24}}{{15}} - \frac{{11}}{{15}} = \frac{{13}}{{15}}\)
محاسبه ی کل عبارت:\(\left( {3\frac{3}{5} - 2\frac{{11}}{5}} \right) \div 1\frac{3}{{10}} = \frac{{13}}{{15}} \div \frac{{13}}{{10}} = \frac{{13}}{{15}} \times \frac{{10}}{{13}} = \frac{2}{3}\)
ب\(\frac{9}{{11}} - \frac{9}{{11}} \div \frac{{22}}{{27}}\)
در این عبارت، در ابتدا باید حاصل تقسیم \(\frac{9}{{11}} \div \frac{{22}}{{27}}\) را به دست آوریم. دقت داشته باشید که در هر عبارت محاسباتی، باید حاصل ضرب و تقسیم را زودتر از جمع و تفریق به دست آوریم.
\(\frac{9}{{11}} - \frac{9}{{11}} \div \frac{{22}}{{27}} = \frac{9}{{11}} - \frac{9}{{11}} \times \frac{{22}}{{27}} = \frac{{{9_{ \times 3}}}}{{{{11}_{ \times 3}}}} - \frac{{{2_{ \times 11}}}}{{{3_{ \times 11}}}} = \frac{{27}}{{33}} - \frac{{22}}{{33}} = \frac{5}{{33}}\)
ج\(\frac{{\frac{9}{{20}}}}{{\frac{3}{{25}}}}\)
\(\frac{{\frac{9}{{20}}}}{{\frac{3}{{25}}}} = \frac{9}{{20}} \div \frac{3}{{25}} = \frac{9}{{20}} \times \frac{{25}}{3} = \frac{{15}}{4}\)
برای حل چنین سؤالاتی ابتدا باید عبارت های موجود در صورت و مخرج کسر را به طور جداگانه محاسبه کنیم، سپس با استفاده از نکته ،قبل حاصل کل عبارت را به دست آوریم.
مقایسه ی کسرها
فصل 2 : کسر
مقایسه ی کسرها
در مقایسه ی کسرها، سه حالت زیر اتفاق می افتد:
حالت اول در کسرهایی که مخرج آنها مساوی است کسری بزرگ تر است که صورت آن بزرگ تر باشد.
\(\frac{3}{7}\left\lfloor {\, < \,} \right\rfloor \frac{5}{7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{12}}{{13}}\left\lfloor {\, > \,} \right\rfloor \frac{9}{{13}}\)
حالت دوم در کسرهایی که صورت آنها مساوی است کسری بزرگ تر است که مخرج آن کوچک تر باشد.
\(\frac{3}{5}\left\lfloor {\, < } \right\rfloor \frac{3}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{15}}{7}\left\lfloor {\, > \,} \right\rfloor \frac{{15}}{{20}}\)
حالت سوم برای مقایسه ی کسرهایی که نه صورت و نه مخرج های برابر دارند ابتدا هر دو کسر را هم مخرج یا هم صورت میکنیم سپس کسرها را مانند حالت اول یا دوم مقایسه میکنیم.
\(\frac{{25}}{{18}}\left\lfloor {\,\,} \right\rfloor \frac{{17}}{{12}} \to \frac{{{{25}_{ \times 2}}}}{{{{18}_{ \times 2}}}}\left\lfloor {\,\,} \right\rfloor \frac{{{{17}_{ \times 3}}}}{{{{12}_{ \times 3}}}} \to \frac{{50}}{{36}} < \frac{{51}}{{36}}\)
در مقایسه ی عددهای مخلوط ابتدا قسمت های صحیح سپس قسمت های کسری که کوچک تر از واحد هستند را با هم مقایسه میکنیم.
\(3\frac{4}{5} > 3\frac{3}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\frac{7}{{10}} < 3\frac{1}{{10}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7\frac{3}{7} < 7\frac{3}{4}\)
مثال
اعداد زیر را از کوچک به بزرگ مرتب کنید.
\(3\frac{1}{3},\frac{3}{5},\frac{2}{3},\frac{5}{4},1,\frac{{11}}{6},\frac{7}{2},\frac{4}{7}\)
برای حل چنین سؤالاتی بهتر است در ابتدا عددهای کوچک تر از واحد را جداگانه و عددهای بزرگ تر از واحد را نیز جداگانه مقایسه کنیم.
عددهای کوچک تر از واحد:
\(\begin{array}{l}\frac{3}{5},\frac{2}{3},\frac{4}{7} \to \frac{{{3_{ \times 21}}}}{{{5_{ \times 21}}}},\frac{{{2_{ \times 35}}}}{{{3_{ \times 35}}}},\frac{{{4_{ \times 15}}}}{{{7_{ \times 15}}}} \to \frac{{63}}{{105}},\frac{{70}}{{105}},\frac{{60}}{{105}}\\\\\frac{{60}}{{105}} < \frac{{63}}{{105}} < \frac{{70}}{{105}} \to \frac{4}{7} < \frac{3}{5} < \frac{2}{3}\end{array}\)
عددهای بزرگتر از واحد:
\(\begin{array}{l}3\frac{1}{3},\frac{5}{4},\frac{{11}}{6},\frac{7}{2} \to \frac{{{{10}_{ \times 4}}}}{{{3_{ \times 4}}}},\frac{{{5_{ \times 3}}}}{{{4_{ \times 3}}}},\frac{{{{11}_{ \times 2}}}}{{{6_{ \times 2}}}},\frac{{{7_{ \times 6}}}}{{{2_{ \times 6}}}} \to \frac{{40}}{{12}},\frac{{15}}{{12}},\frac{{22}}{{12}},\frac{{42}}{{12}}\\\\ \to \frac{{15}}{{12}} < \frac{{40}}{{12}} < \frac{{22}}{{12}} < \frac{{42}}{{12}} \to \frac{5}{4} < \frac{{11}}{6} < \frac{{10}}{3} < \frac{7}{2}\end{array}\)
بنابراین عددها به ترتیب مقابل هستند:
\(\frac{4}{7} < \frac{3}{5} < \frac{2}{3} < \frac{5}{4} < \frac{{11}}{6} < \frac{{10}}{3} < \frac{7}{2}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
اعداد اعشاری
فصل 3 : اعداد اعشاری
عدد اعشاری
یادآوری
به کسرهایی که مخرج آنها ۱۰ یا ۱۰۰ یا ۱۰۰۰ و ... باشند کسرهای اعشاری میگویند. کسرهای اعشاری را می توان به صورت عدد اعشاری نوشت.
مثال
کسر اعشاری \(\frac{{273}}{{100}}\) را به صورت عدد اعشاری بنویسید.
\(\frac{{273}}{{100}} = 2/73\)
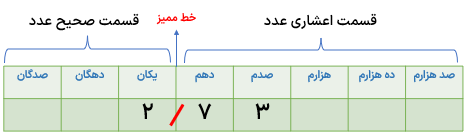
هر عدد اعشاری از دو جزء یا دو قسمت تشکیل شده است جزء صحیح یا قسمت صحیح عدد و جزء اعشاری یا قسمت اعشاری عدد.
برای مثال در عدد ۲/۷۳ داریم:
اگر این عدد را در جدول ارزش مکانی قرار دهیم، به صورت زیر است:
مثال
عدد ۳/۴ را به وسیله ی شکل نمایش دهید.
در این عدد واحد به ۱۰ قسمت مساوی تقسیم شده، یعنی \(1 = \frac{{10}}{{10}}\) واحد.
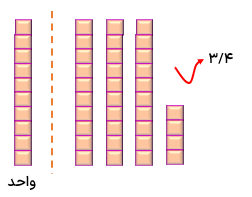
\(3/4 = 3 + 0/4 = 3 + 0/1 + 0/1 + 0/1 + 0/1\)
در سال های قبل با اعداد اعشاری آشنا شدید و دیدید که این اعداد کاربردهای زیادی در زندگی روزمره ی ما و در زمینه های مختلف دارند به طور مثال برای بیان رکوردهای ورزشی از عددهای اعشاری استفاده می شود. همچنین از این اعداد در بیان ، ارتفاع ، وزن نمره ی درسی و ... استفاده می کنیم.
هر عدد اعشاری دارای دو قسمت است:
۱ قسمت صحیح این قسمت در سمت چپ خط اعشار ممیز) قرار میگیرد مانند: ۷۰۴/۰۲۸ یا ۱۳/۶۹
۲ قسمت اعشاری: این قسمت در سمت راست خط اعشار ممیز) قرار میگیرد مانند: ۷۰۴/۰۲۸ یا ۱۳/۶۹
به کسرهایی که مخرج آنها ۱۰، ۱۰۰، ۱۰۰۰ یا ... باشد کسر اعشاری می گویند مانند: \(\frac{{125}}{{1000}}\,\,,\,\,\,\frac{{125}}{{100}}\,\,,\,\,\,\frac{{125}}{{10}}\) کسرهای اعشاری را میتوان به صورت عددهای اعشاری در جدول ارزش مکانی نوشت به این ترتیب کسرهای اعشاری بالا را می توانیم به صورت ۱۳/۵ ۱/۳۵ و ۰/۱۳۵ هم بنویسیم و آنها را به صورت زیر بخوانیم:
۱۳/۵ : سیزده و پنج صدم یا سیزده و نیم
۱/۳۵: یک وسی و پنج صدم
۰/۱۳۵ :صد و سی و پنج هزارم
هر عدد اعشاری را میتوان هم با شکل و هم روی محور نمایش داد به شکلهای زیر و عدد اعشاری نمایش داده شده توسط آنها دقت کنید.
مثال
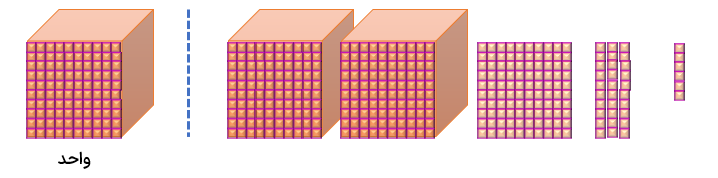
عدد ۲/۱۳۵ را هم با شکل و هم در جدول ارزش مکانی نمایش دهید.
مثال
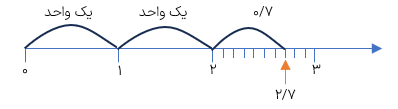
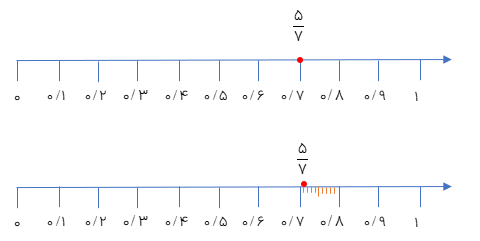
عدد ۲/۷ را روی محور نمایش دهید.
برای نمایش یک عدد اعشاری مانند ۲/۷ روی محور باید مراحل زیر را انجام دهیم:
۱ محور اعداد را رسم کرده و واحدها را روی آن مشخص کنیم.
۲ به اندازه ی قسمت صحیح عدد اعشاری مورد نظر یعنی ۲ واحد از صفر شروع به شمردن واحدها می
کنیم.
3 با توجه به قسمت اعشاری عدد مورد نظر (که در این جا ۰/۷ است) روی محور بین ۲ و ۳ را به ۱۰ قسمت مساوی تقسیم میکنیم به این ترتیب هر قسمت ۰/۱ میشود پس ۷ تا ۰/۱ شمرده و به جلو می رویم تا نقطه ی نمایش عدد ۲/۷ مشخص شود.
صفر در قسمت اعشاری
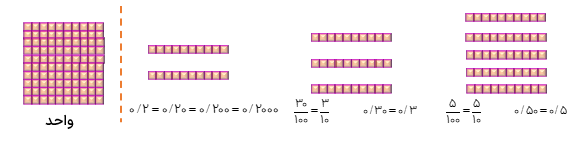
به شکل های زیر و تساوی های نوشته شده دقت کنید.
تساوی های بالا نشان میدهند که اگر بعد از آخرین رقم اعشاری هر عددی به تعداد دلخواه صفر قرار دهیم، آن عدد هیچ تغییری نمی.کند از این خاصیت در جمع تفریق و تقسیم عددهای اعشاری استفاده می کنیم. نکته اگر در بین رقم های اعشاری ،عددی صفر قرار دهیم آن عدد تغییر میکند به طور مثال هیچ یک از عددهای ۳/۷۵، ۳/۰۷۵ و ۳/۷۰۵ با یک دیگر برابر نیستند.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
نوشتن اعداد اعشاری
فصل 3 : اعداد اعشاری
نوشتن عددهای اعشاری از رقم به حروف
برای خواندن عددهای اعشاری ابتدا قسمت صحیح عدد را مانند عددهای طبیعی معمولی می خوانیم، سپس قسمت اعشاری را نیز مانند عدد صحیح میخوانیم اما با توجه به تعداد رقم های اعشار آن در انتهای عبارت کلمه ی دهم یا صدم یا هزارم و ... را قرار میدهیم برای مثال اگر عدد دارای دو رقم اعشار ،باشد، پس از خواندن قسمت صدم و اگر عدد دارای سه رقم اعشاری باشد پس از خواندن قسمت اعشاری کلمه ی هزارم را به کار می بریم.
مثال
عدد 493/059 را بخوانید. (به حروف بنویسید.)
چهارصد و نود و سه و پنجاه و نه هزارم (چون عدد دارای سه رقم اعشار است).
به روش خواندن این دو عدد دقت کنید.
پنجاه و نه صدم\(0/59 \Rightarrow \)
پنجاه عدد صحیح و نه صدم\(50/09 \Rightarrow \)
اگر عدد قسمت ب را بخواهیم به روش گفته شده بخوانیم ممکن است دچار اشتباه شویم و هر یک از عددهای قسمت الف یا ب را بنویسیم برای جلوگیری از این اشتباه اگر در این گونه موارد عدد صحیح صفر نبود، بعد از خواندن عدد قسمت صحیح، عبارت عدد صحیح را می نویسیم.
مثال
هشتاد و شش هزارم\(0/086 \Rightarrow \)
هشتاد عدد صحیح و شش هزارم\(80/006 \Rightarrow \)
بیست و پنج صدم\(0/25 \Rightarrow \)
بیست عدد صحیح و پنج صدم\(20/05 \Rightarrow \)
نوشتن اعداد اعشاری از حروف به رقم
در این حالت بهتر است از جدول ارزش مکانی استفاده کنیم و هر رقم را در مرتبه ی خودش قرار دهیم.
مثال
عدد صد و سی و چهار و هفتاد و شش صدم را به رقم بنویسید.
نوشتن عددهای اعشاری به صورت کسر
ابتدا كل رقم های عدد را بدون ممیز در صورت کسر قرار میدهیم و سپس در مخرج کسر، عدد ۱ را قرار می دهیم و در سمت راست عدد ۱ به تعداد رقم های اعشار، صفر قرار می دهیم.
مثل عدد ۵۲/۱۹۵ به این صورت میشود:
\(\frac{{52195}}{{1000}}\)
نوشتن کسرها به صورت عددهای اعشاری
الف: اگر مخرج کسر ۱۰ یا ۱۰۰ یا ۱۰۰۰ یا ... باشد، ابتدا عدد صورت کسر را می نویسیم و سپس به تعداد صفرهای مخرج از سمت راست، ممیز می زنیم.
مثال
عدد\(\frac{{4273}}{{1000}}\) را به صورت اعشاری بنویسید.
\(\frac{{4273}}{{1000}} = 4/273\)
اگر مخرج کسر10 یا 100 یا 1000 و00 نبود برای تبدیل کسر به اعشاری ابتدا باید باضرب صورت و مخرج در عدد مناسب مخرج کسر را به ۱۰ یا ۱۰۰ یا ۱۰۰۰ و ۰۰ تبدیل کنیم و سپس کسر اعشاری را به صورت عدد اعشاری بنویسیم برای راحتی کار بهتر است که ضرب های مقابل را به خاطر بسپارید.
2×5=10
4×25=100
8×125=1000
مثال
کسرهای زیر را به عدد اعشاری تبدیل کنید.
\(\begin{array}{l}\frac{3}{5} \Rightarrow \frac{{3 \times 2}}{{5 \times 2}} = \frac{6}{{10}} = 0/6\\\\\frac{{43}}{{25}} \Rightarrow \frac{{43 \times 4}}{{25 \times 4}} = \frac{{172}}{{100}} = 1/72\\\\\frac{{12}}{{125}} \Rightarrow \frac{{12 \times 8}}{{125 \times 8}} = \frac{{96}}{{1000}} = 0/096\end{array}\)
گاهی اوقات ممکن است که نتوانیم مخرج را با ضرب عددها به ۱۰ یا ۱۰۰ یا ۱۰۰۰ تبدیل کنیم و در این صورت یا باید ابتدا در صورت امکان کسر را ساده کنیم و یا اگر این کار ممکن نباشد با تقسیم صورت کسر بر مخرج، آن را به عدد اعشاری تبدیل کنیم.
مثال
عدد \(\frac{{21}}{{12}}\) را به صورت عدد اعشاری بنویسید.
\(\frac{{21 \div 3}}{{12 \div 3}} = \frac{7}{4} = 1\frac{3}{4} \to 1\frac{{3 \times 25}}{{4 \times 25}} = 1\frac{{75}}{{100}} = 1/75\)
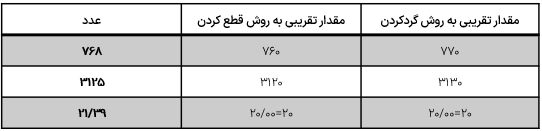
مقایسه ی عددهای اعشاری
فصل 3 : اعداد اعشاری
مقایسه ی عددهای اعشاری
برای مقایسه ی اعداد اعشاری ابتدا قسمت صحیح آنها را مقایسه میکنیم هر عددی که قسمت صحیح آن بزرگ تر باشد، آن عدد بزرگ تر است. اگر قسمتهای صحیح دو عدد مساوی باشند، به ترتیب دهم، صدم و هزارم و ... آن ها را مقایسه میکنیم دهم هر عددی که بزرگ تر بود آن عدد بزرگ تر است و اگر دهم ها نیز مساوی باشند، صدم هر عددی که بزرگ تر باشد آن عدد بزرگ تر است و ....
مثال
\(\begin{array}{l}5/783\,\,\,\,\, > \,\,\,\,\,\,2/9999\\\\0/9876\,\,\,\,\,< \,\,\,\,\,\,1/7\end{array}\)
مثال
عددهای اعشاری زیر را مقایسه می کنیم.
\(9/01\,\,\left\lfloor {\,\,} \right\rfloor \,\,8/9873 \to 9/01 > 8/9873\)
چون عدد صحیح ۹ بزرگ تر از عدد صحیح ۸ است پس عدد ۹/۰۱ از عدد ۸/۹۸۷۳ بزرگ تر است.
\(19/3874\,\,\left\lceil {\,\,} \right\rceil \,\,19/3859 \to 19/3874 > 19/3859\)
چون قسمت های صحیح و رقم های دهم و صدم دو عدد مساوی است بنابراین رقم هزارم آن ها را مقایسه می کنیم.
اگر رقم دهم یک عدد اعشاری کوچک تر از یک از ۴ بیشتر باشد آن عدد از نصف کم تر نیست ( یا مساوی نصف است و یا از نصف بیشتر است) مانند:
بزرگ تر از نصف هستند\(0/6\,\,\,,\,\,\,0/8000002\,\,,\,\,\,0/73 \Rightarrow \)
نصف = ۰/۵۰۰
در صورتی که قسمت صحیح دو عدد برابر بود دهم ها را با هم مقایسه میکنیم عددی بزرگ تر است که دهم آن بزرگ تر باشد.
در صورت تساوی دهم ها باید صدمها را مقایسه کنیم و این عمل را تا جایی ادامه دهیم که عدد بزرگ تر معلوم شود.
\(5/7\,\,\,\, > \,\,\,\,5/37\,\,\,\,\,\,\,\,\,\,\,\,\,13/235\,\,\,\, < \,\,\,\,13/25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7/029\,\,\,\, > \,\,\,\,7/0258\)
مثال
۱۰ کارت با رقم های ۰ تا ۹ و یک کارت با نماد ممیز داریم:
الف اگر عدد ۵۱ را در سمت چپ ممیز بسازیم با ۵ کارت دیگر در قسمت اعشاری (سمت راست ممیز) نزدیک ترین عدد ممکن به ۵۱ را بسازید.
ب اگر عدد ۵۱ را در سمت چپ ممیز بسازیم با ۵ کارت دیگر در قسمت اعشاری (سمت راست ممیز) نزدیک ترین عدد ممکن به ۵۲ را بسازید.
مثال
گسترده عدد اعشاری به چه صورت نمایش داده می شود؟
الف \(52/03 \)
\(52/03 = 50 + 2 + 0/03\)
ب\(412/019 \)
\(412/019 = 400 + 10 + 2 + 0/1 + 0/009\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
جمع و تفریق عددهای اعشاری
فصل 3 : اعداد اعشاری
جمع و تفریق عددهای اعشاری
در جمع و تفریق عددهای اعشاری باید دقت کنیم که ممیزها خیلی دقیق زیر هم قرار گیرند. به این ترتیب رقم های هم مرتبه نیز زیر هم قرار میگیرند؛ یعنی یکان ها زیر ،هم دهم ها زیر هم صدم ها زیر هم و ...
مثال
حاصل جمع و تفریق های زیر را حساب کنید.
18/29+3/4
ابتدا عددها را در جدول ارزش مکانی قرار میدهیم تا رقم های هم مرتبه زیر هم قرار گیرند.
7/1-2/76
در سال قبل با روش های مختلف محاسب هی جمع و تفریق عددهای اعشاری از قبیل رسم شکل، رسم محور، تبدیل به کسر گسترده نویسی و روش جدول ارزش مکانی یا همان زیر هم نویسی آشنا شدید و ملاحظه کردید که روش زیر هم نویسی سریع ترین و ساده ترین روش محاسبه بود در این روش با توجه به ارزش مکانی عددها، باید ممیزها زیر هم و عددهای هم مرتبه ی هم زیر هم نوشته شوند؛ یعنی یکان ها را زیر هم دهم ها را زیر همدیگر و ... بنویسیم سپس از کم ترین مرتبه جمع یا تفریق مورد نظر را انجام دهیم و هر کجا که به ممیز رسیدیم، در جواب هم ممیز را بنویسیم دقت داشته باشید که اگر عددی ممیز نداشته باشد، باید در سمت راست آن ممیز قرار دهیم.
مثال
حاصل جمع ها و تفریق های زیر را بدست آورید.
الف\(5/43 + 17/6\)
\(\begin{array}{l}\,\,\,\,\,\,\,5/43\\ + \,\,\,\,\,17/60\\ - - - - - - - - \\\,\,\,\,\,\,\,\,23/03\end{array}\)
ب\(18 - 5/43\)
\(\begin{array}{l}\,\,\,\,\,\,18/00\\ - \,\,\,\,\,5/43\\ - - - - - - - \\\,\,\,\,\,\,12/57\end{array}\)
ج\(724/5 + 72/45\)
\(\begin{array}{l}\,\,\,\,\,724/50\\ + \,\,\,\,\,72/45\\ - - - - - - - - \\\,\,\,\,\,796/95\end{array}\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
تبدیل کسر و عدد اعشاری به یکدیگر
فصل 3 : اعداد اعشاری
تبدیل کسر اعشاری به عدد اعشاری
برای تبدیل کسرهایی مانند \(\frac{{75}}{{10}}\) و\(\frac{3}{{100}}\) و\(\frac{{243}}{{1000}}\) و... که مخرج آن ها ۱۰، ۱۰۰، ۱۰۰۰ و .. می باشد به عدد اعشاری، ابتدا صورت کسر را مینویسیم و به تعداد صفرهای مخرج از سمت راست عدد رقم های اعشاری را جدا کرده و ممیز می زنیم.
\(\frac{{75}}{{10}} = 7/5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{3}{{100}} = 0/03\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{243}}{{1000}} = 0/243\)
در تبدیل کسرهایی مانند ، و که مخرج آن ها ۱۰، ۱۰۰، ۱۰۰۰ و ... نیست) به عدد اعشاری، باید با توجه به تساوی کسرها صورت و مخرج کسر را در عددی ضرب کنیم تا مخرج کسر حاصل یکی از عددهای ۱۰،۱۰۰, 000ا و ... شود و کسر اعشاری به دست آید.
\(\frac{3}{5} = \frac{6}{{10}} = 0/6\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{7}{4} = \frac{{175}}{{100}} = 1/75\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{17}}{{125}} = \frac{{136}}{{1000}} = 0/136\)
تبدیل عدد اعشاری به کسر اعشاری
ابتدا عدد را بدون ممیز در صورت کسر می نویسیم و در مخرج کسر به تعداد رقم های اعشاری عدد، جلوی عدد یک، صفر می گذاریم.
\(37/452 = \frac{{37452}}{{1000}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,892/75 = \frac{{89275}}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,879/6 = \frac{{8796}}{{10}}\)
ضرب عددهای اعشاری
فصل 3 : اعداد اعشاری
ضرب عددهای اعشاری
برای ضرب عددهای اعشاری در حالت کلی ابتدا عددها را بدون در نظر گرفتن ممیز مانند دو عدد صحیح در هم ضرب می کنیم و سپس مجموع تعداد ارقام اعشاری دو عدد را حساب کرده و به همان تعداد از سمت راست در حاصل ضرب اعشار میزنیم.
مثال
حاصل ضرب مقابل را حساب کنید.
۲/۴ × ۱/۵۱
ابتدا حاصل ۱۵۱ × ۲۴ را حساب می کنیم:
۲۴ × ۱۵۱ = ۳۶۲۴
چون دو عدد روی هم سه رقم اعشار دارند بنابراین در حاصل ضرب از سمت راست، سه رقم اعشار می زنیم:
2/4×1/51=3/624
ضرب عددهای اعشاری به وسیله ی تبدیل اعداد اعشاری به کسر
مثال
حاصل ضرب مقابل را حساب کنید.
3/8×2/74
\(3/8 \times 2/74 = \frac{{38}}{{10}} \times \frac{{274}}{{100}} = \frac{{10412}}{{1000}} = 10/412\)
ضرب عددهای اعشاری به وسیله ی شکل
مثال
حاصل ضرب مقابل را به وسیله ی شکل حساب کنید.
5×0/3
مثال
با توجه به واحد حاصل ضرب های زیر را به وسیله ی شکل حساب کنید.
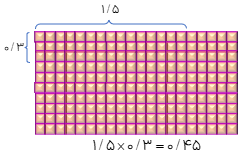
الف0/4×0/7
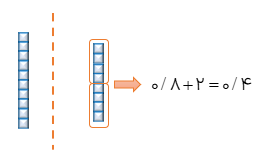
ب1/5×0/3
۴۵ تا مربع کوچک رنگ شده که هر کدام نشانه ی ۰/۰۱ است.
ضرب عددهای اعشاری به کمک مساحت (روش مساحتی)
مثال
حاصل ضرب مقابل را حساب کنید.
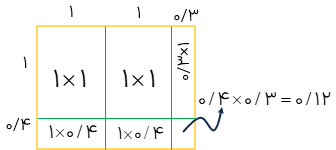
1/8×2/3
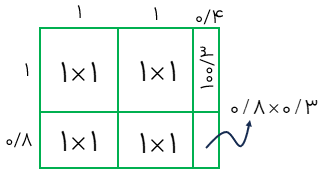
\(\begin{array}{l}1/8 \times 2/3 = (1 \times 1) + (1 \times 1) + (1 \times 0/8) + (1 \times 0/3) + (0/8 \times 0/3)\\ = 1 + 1 + 0/8 + 0/8 + 0/3 + 0/24 = 4/14\end{array}\)
در سال قبل با روش های مختلف محاسبه ی ضرب عددهای اعشاری آشنا شدید در این بخش به یادآوری آن ها می پردازیم.
روش اول
برای محاسبه ی حاصل ضرب یک عدد صحیح در یک عدد اعشاری (مانند ۰/۴ × ۳) می توانیم از شکل زیر استفاده کنیم و با شمارش خانه ها مقدار حاصل ضرب را که ۱/۲ می باشد، حساب کنیم.
۳×۰/۴ = ۱/۲
روش دوم (تبدیل به کسر)
در این روش ابتدا اعداد اعشاری را به صورت کسری می نویسیم، سپس حاصل ضرب کسرها را ابتدا بدون ساده کردن آنها به دست می آوریم و در آخر جواب را به صورت اعشاری می نویسیم.
مثال
به مثال های زیر دقت کنید.
الف\(5/3 \times 0/25 = \frac{{53}}{{10}} \times \frac{{25}}{{100}} \times \frac{{1325}}{{1000}} = 1/325\)
ب\(0/2 \times 7/5 \times 12/3 = \frac{2}{{10}} \times \frac{{75}}{{10}} \times \frac{{123}}{{10}} = \frac{{18450}}{{1000}} = 18/450 = 18/45\)
روش سوم (مساحتی)
در این روش برای محاسبه ی حاصل ضرب عددهایی مانند ۲/۳ و ۱/۴، ابتدا یک مستطیل رسم می کنیم طوری که طول مستطیل با عدد بزرگ تر و عرض آن با عدد کوچک تر برابر مستطیل را مانند شکل زیر تقسیم بندی و مساحت تمامی قسمت ها را با هم جمع می باشد. سپس کنیم به این ترتیب حاصل ضرب دو عدد به دست می آید.
مثال
\(\begin{array}{l}2/3 \times 1/4 = (2 \times 1) + (2 \times 0/4) \times 0/3 +0/12\\ = 2 + 0/8 + 0/3 + 0/12 = 3/22\end{array}\)
روش چهارم (فرآیندی):
در این روش ابتدا عددها را بدون در نظر گرفتن ممیزها در یک دیگر ضرب می کنیم سپس به تعداد رقم های اعشاری کل ،عددها در جواب به دست آمده از سمت راست اعشار می زنیم.
الف5/3×0/25=1/325
ابتدا حاصل ضرب ۲۵ × ۵۳ را حساب میکنیم که برابر ۱۳۲۵ می،شود چون ۵/۳ دارای یک رقم اعشاری و ۰/۲۵ هم دارای دو رقم اعشاری است برای جواب ضرب یعنی ۱۳۲۵ از سمت راست سه رقم شمرده و ممیز را می زنیم.
ب\(0/2 \times 7/5 \times 12/3 = 2 \times 75 \times 123 = 18450 \Rightarrow 0/2 \times 7/5 \times 12/3 = 18/450\)
۱ برای ضرب هر عدد اعشاری در عددهای ۱۰، ۱۰۰، ۱۰۰۰ و ... . ابتدا خود عدد را می نویسیم، سپس ممیز را به تعداد صفرها به سمت راست (جلو) انتقال میدهیم یعنی اگر عدد را در ۱۰ ضرب کردیم، باید ممیز را یک رقم به جلو منتقل کنیم و اگر در ۱۰۰ ضرب کردیم باید ممیز را دو رقم به سمت جلو منتقل کنیم و .....
54/327×10=543/27
54/327×100=5432/7
54/327×1000=54327
54/327×10000=543270
۲ اگر هر عدد اعشاری را در ۰/۱۰ ضرب کنیم ممیز آن یک رقم به سمت چپ (عقب) منتقل می شود و اگر در ۰/۰۱ ضرب کنیم، ممیز آن عدد دو رقم به سمت چپ منتقل می شود و ....
54/327×0/1=5/4327
54/327×0/01=0/54327
54/327×0/001=0/054327
54/327×0/0001=0/0054327
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تقسیم عددهای اعشاری
فصل 3 : اعداد اعشاری
تقسیم عددهای اعشاری به وسیله ی شکل
مثال
حاصل تقسیم مقابل را به وسیله ی شکل حساب کنید.
0/8÷2
مثال
حاصل تقسیم مقابل را به وسیله ی شکل حساب کنید.
0/24÷3
تقسیم اعشاری
برای انجام تقسیم اعشاری بر یک عدد صحیح مانند 1/2÷4 میتوانیم از روش های زیر استفاده کنیم:
روش اول (رسم شکل)
در این روش شکل مربوط به عدد اعشاری را رسم کرده، سپس آن را به قسمت های خواسته شده تقسیم بندی می کنیم.
روش دوم (تبدیل به کسر)
در این روش ابتدا عددهای اعشاری را به صورت کسری می نویسیم، سپس حاصل تقسیم کسرها را به دست می آوریم و در آخر در صورت ،نیاز جواب را به صورت اعشاری می نویسیم.
مثال
\(\begin{array}{l}1)\,\,1/2 \div 4 = \frac{{12}}{{10}} \div 4 = \frac{{12}}{{10}} \times \frac{1}{4} = \frac{3}{{10}} = 0/3\\\\2)\,\,2/97 \div 99 = \frac{{297}}{{100}} \div 99 = \frac{{297}}{{100}} \times \frac{1}{{99}} = \frac{3}{{100}} = 0/03\\\\3)\,\,0/441 \div 7 = \frac{{4441}}{{1000}} \div 7 = \frac{{441}}{{1000}} \times \frac{1}{7} = \frac{{63}}{{1000}} = 0/063\end{array}\)
روش سوم
در این روش تقسیم را مانند یک تقسیم معمولی انجام میدهیم و هرگاه در مقسوم به ممیز رسیدیم در خارج قسمت نیز ممیز میزنیم دقت داشته باشید که در این گونه تقسیم ها، همواره تعداد ارقام اعشاری خارج قسمت و باقی مانده با تعداد ارقام اعشاری مقسوم برابر است.
برای تقسیم هر عدد اعشاری بر عددهای ۱۰، ۱۰۰، ۱۰۰۰ و . .... ابتدا خود عدد را می نویسیم، سپس ممیز را به تعداد صفرها به سمت چپ (عقب) انتقال میدهیم یعنی اگر عدد را بر ۱۰ تقسیم کنیم، باید ممیز را یک رقم به عقب منتقل کنیم و اگر عدد را بر ۱۰۰ تقسیم کنیم باید ممیز را دو رقم به عقب منتقل کنیم و ...
\(\begin{array}{l}794/63 ÷ 10 = 79/463\\794/63 ÷ 100 = 7/9463\\794/63 ÷ 1000 = 0/79463\\794/63 ÷ 10000 = 0/079463\end{array}\)
مثال
حاصل تقسیم مقابل را به کمک شکل حساب کنید.
یادآوری تقسیم
برای اطمینان از درستی عمل تقسیم دو روش برای امتحان آن وجود دارد که به آن ها رابطه های تقسیم میگویند. توجه کنید که حتما باید هر رابطه را برای یک تقسیم بنویسیم و هر دو رابطه درست باشند.
رابطه 1: (خارج قسمت ×مقسوم علیه)+باقی مانده=مقسوم
رابطه 2: باقی مانده<مقسوم علیه
مثال
آیا تقسیم مقابل درست انجام شده است؟
رابطه های تقسیم را می نویسیم:
رابطه ی اول نشان میدهد که تقسیم درست انجام شده است
رابطه 1: 1×6+9=15 رابطه درست است
رابطه 2: غلط است زیرا باقی مانده کوچک تر از مقسوم علیه نیست 9>1
چون باقی مانده از مقسوم علیه کوچک تر نیست پس رابطه ی دوم غلط و در نتیجه تقسیم غلط انجام شده است.
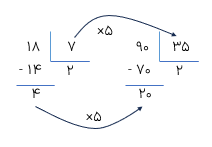
اگر مقسوم و مقسوم علیه تقسیمی را در یک عدد عدد غیر صفر ضرب کنیم خارج قسمت تغییر نمی کند، اما باقی مانده در همان عدد ضرب می شود.
مثال
در تقسیم زیر مقسوم و مقسوم علیه را ۵ برابر کرده ،ایم خارج قسمت تغییر نمیکند، اما باقی مانده ۵ برابر می شود.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
تقسیم عدد اعشاری بر عدد طبیعی
فصل 3 : اعداد اعشاری
تقسیم عدد اعشاری بر عدد طبیعی
در این حالت باید دقت کنیم که خارج قسمت تقسیم را باید تا چند رقم اعشار انجام دهیم. اگر تعداد رقم های اعشاری خواسته شده ی خارج قسمت بیشتر از تعداد رقم های اعشاری مقسوم ،باشد با قرار دادن صفر در سمت راست رقم های اعشاری ،مقسوم تعداد رقم های اعشاری مقسوم را با تعداد رقم های اعشاری خارج قسمت برابر می کنیم.
مثال
تقسیم مقابل را تا یک رقم اعشار در خارج قسمت انجام دهید.
چون مقسوم دارای یک رقم اعشار است و می خواهیم تقسیم را نیز تا یک رقم اعشار در خارج قسمت انجام دهیم پس نیازی به قراردادن صفر در مقسوم نیست برای دقت در انجام عمل تقسیم و جلوگیری از اشتباه های احتمالی، خط ممیز را رسم می کنیم. خط ممیز نشان دهنده ی ممیز عددها در تمام مراحل تقسیم و از جمله رقم های اعشاری باقی مانده است.
مثال
تقسیم مقابل را تا دو رقم اعشار در خارج قسمت انجام دهید و باقی مانده را نیز مشخص کنید.
چون باید تقسیم تا دو رقم اعشار در خارج قسمت انجام شود و مقسوم دارای یک رقم اعشار است. پس یک صفر در سمت راست رقم یک قرار تا مقسوم هم دارای دو رقم اعشار شود.
1 هنگامی که رقم ۱ را پایین می آوریم چون رقم ۱، رقم بعد از ممیز در مقسوم است، به همین دلیل در خارج قسمت ممیز می زنیم و تقسیم را ادامه می دهیم.
2 تعداد رقم های اعشاری باقی مانده با تعداد رقم های اعشاری مقسوم، باید برابر باشد.
تقسیم به کمک رسم شکل
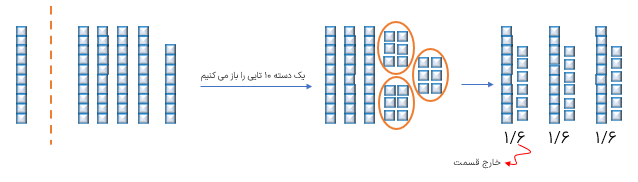
برای تقسیم عددی اعشاری مانند ۴/۴۷ بر ۳ به صورت زیر عمل می کنیم:
ابتدا با توجه به این که کوچک ترین مرتبه ی این عدد صدم میباشد پس هر واحد را به صد قسمت مساوی تقسیم می کنیم و شکل مربوط به این عدد اعشای را رسم میکنیم.
حالا سه تا از واحدهای کامل را انتخاب میکنیم و به هر دسته یک واحد میدهیم یکی از واحدهای کامل باقی ماند که باید آن را باز کنیم و به ده تا ۰/۱ تبدیل کنیم به این ترتیب ۱۴ تا ۰/۱ به وجود می آید. این ۱۴ تا ۰/۱ را به سه قسمت مساوی تقسیم میکنیم که دو تا ۰/۱ باقی می ماند.
حالا دو دسته ۰/۱ باقی مانده را نیز باز میکنیم به این ترتیب ۲۷ تا ۰/۰۱ باقی می ماند که باید آن را به سه قسمت مساوی تقسیم کنیم.
در اخر ملاحظه می کنید که اگر 4/74 را به سه قسمت مساوی تقسیم کنیم هر قسمت مساوی 1/4 خواهد شد.
تقسیم به روش محاسباتی
در این روش ابتدا خط ممیز را رسم میکنیم این خط نشان دهنده ی تمام ممیزهایی است که در انجام تقسیم در عددها قرار میگیرد سپس تقسیم را مانند تقسیم معمولی انجام میدهیم و هرگاه در مقسوم به ممیز رسیدیم، در خارج قسمت هم ممیز میزنیم. دقت داشته باشید که در این گونه تقسیم،ها همواره تعداد ارقام اعشاری خارج قسمت و باقی مانده با تعداد ارقام اعشاری مقسوم برابر است.
مثال
به تقسیم های زیر دقت کنید.
پیشروی در تقسیم
گاهی اوقات برای آن که جواب دقیق تری از تقسیم به دست آید می توانیم در سمت راست قسمت اعشاری مقسوم به تعداد مورد نیاز صفر قرار داده و تقسیم کردن را ادامه دهیم به این ترتیب خارج قسمت دقیق تری به دست می آید. در اصطلاح به این عمل پیشروی در تقسیم می گوییم.
مثال
به تقسیم های زیر دقت کنید.
مثال
ضخامت کتابی ۲۵۰ صفحه ای ۱/۵ سانتی متر است. ضخامت هر برگ این کتاب چند سانتی متر است؟
دقت داشته باشید که ۲۵۰ صفحه یعنی ۱۲۵ برگ هر برگ دو صفحه است کافی است که عدد ۱/۵ را بر ۱۲۵ تقسیم کنیم و با پیشروی در تقسیم، به باقی ماندهی صفر برسیم که ضخامت هر ورق آن ۰/۰۱۲ سانتی متر می شود.
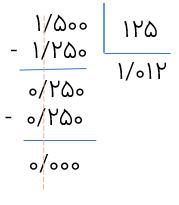
تقسیم یک عدد بر عدد اعشاری
فصل 3 : اعداد اعشاری
تقسیم یک عدد بر عدد اعشاری
در این نوع تقسیم ها ابتدا باید مقسوم و مقسوم علیه را در یکی از اعداد ۱۰ یا ۱۰۰ یا ۱۰۰۰ ضرب کنیم (باتوجه به تعداد رقم های اعشاری مقسوم علیه) تا مقسوم علیه به عدد طبیعی تبدیل شود و سپس باید مانند تقسیم عدد اعشاری بر عدد ،طبیعی تقسیم را انجام دهیم فقط باید دقت کنیم که این تقسیم، تقسیم اصلی نیست تقسیم کمکی است. خارج قسمت تقسیم ،اصلی با خارج قسمت تقسیم کمکی برابر است، اما برای تعیین باقی مانده ی تقسیم ،اصلی باید باقی مانده ی تقسیم کمکی را بر همان عددی که مقسوم و مقسوم عیله در آن ضرب شده، تقسیم کنیم.
مثال
تقسیم مقابل را انجام دهید و باقی مانده را مشخص کنید.
1/4÷0/03
ابتدا مقسوم و مقسوم علیه را در عدد ۱۰۰ ضرب می کنیم تا مقسوم علیه به عدد صحیح تبدیل شود. (توجه کنید که با این کار باقی ماندهی تقسیم نیز ۱۰۰ برابر می شود.)
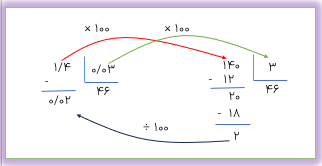
خارج قسمت تقسیم اصلی همیشه با خارج قسمت تقسیم کمکی برابر است برای تعیین تعداد رقم های اعشاری باقی مانده ی اصلی میتوان از روش ساده تری نیز استفاده کرد به این ترتیب که تعداد رقم های اعشاری باقی مانده ی تقسیم با مجموع تعداد رقم های اعشاری مقسوم علیه و خارج قسمت برابر است.
مثال
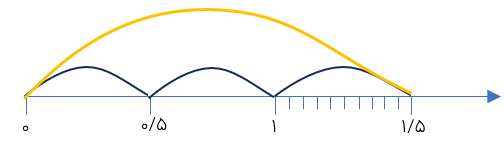
حاصل تقسیم مقابل را با محور حساب کنید.
1/5÷3
چون مقسوم علیه ۰/۵ است هر واحد را به دو قسمت تقسیم می کنیم.
مثال
حاصل تقسیم مقابل را با محور حساب کنید.
\(3 \div 0/25 \)
چون مقسوم علیه ۰/۲۵ است \((0/25 = \frac{1}{4})\) هر واحد را به چهار قسمت تقسیم می کنیم.
\(3 \div 0/25 = 12\)
همان طور که ملاحظه میکنید اگر مقسوم و مقسوم علیه تقسیمی را در عددی غیر از صفر ضرب کنیم، خارج قسمت تغییر نمیکند اما باقی مانده نیز در همان عدد ضرب می شود.
با توجه به خاصیت بالا میتوانیم تقسیم هایی را که مقسوم علیه اعشاری دارند به تقسیمی که مقسوم علیه طبیعی دارند، تبدیل کنیم کافی است که با توجه به تعداد ارقام اعشاری مقسوم علیه هم مقسوم و هم مقسوم علیه را در یکی از عددهای ۱۰، ۱۰۰، ۱۰۰۰ و ضرب کنیم
به این ترتیب، ممیز مقسوم علیه از بین میرود و به عدد صحیح تبدیل میشود و تقسیم به صورت تقسیم درس قبل تبدیل می شود و میتوانیم به سادگی حاصل تقسیم را به دست آوریم.
اگر مقسوم و مقسوم علیه را در ۱۰ ضرب کنیم باقی مانده هم ده برابر میشود و اگر در ۱۰۰ ضرب کنیم، باقی مانده هم صد برابر میشود لذا برای تعیین باقی مانده ی اصلی تقسیم باید باقی مانده ی به دست آمده را بر همان عددی که مقسوم و مقسوم علیه را در آن ضرب کردیم (یعنی ۱۰، ۱۰۰، ۱۰۰۰ و ..) تقسیم کنیم.
مثال
تقسیم مقابل را انجام دهید.
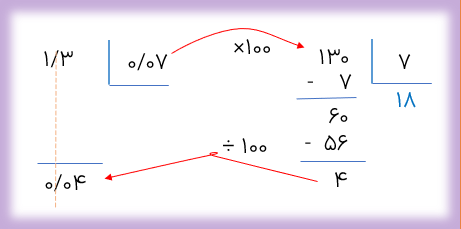
1/3÷0/07
چون کوچک ترین مرتبه ی مقسوم علیه یعنی ،۰/۰۷ صدم ،بود برای تبدیل ۰/۰۷ به عدد صحیح باید ضرب در صد شود.
مثال
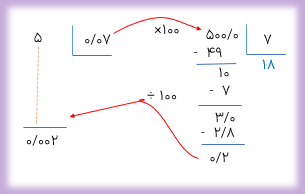
حاصل تقسیم 0/07÷5 را تا یک رقم اعشار در خارج قسمت به دست آورید.
مثال
به کمک ماشین حساب خارج قسمت تقسیم ۰/۷۲ ÷۵/۳ را تا دو رقم اعشار به دست آورید و بدون محاسبه ی تقسیم باقی مانده ی آن را تعیین کنید.
با استفاده از ماشین حساب حاصل تقسیم ۵/۳ بر ۰/۷۲ تا دو رقم اعشار برابر ۷/۳۶ خواهد شد. حالا با استفاده از رابطه ی تقسیم زیر میتوانیم مقدار باقی مانده را به دست آوریم
(مقسوم علیه× خارج قسمت) – مقسوم= باقی مانده
باقی مانده+ (مقسوم علیه× خارج قسمت) = مقسوم
باقی مانده ی تقسیم=\(5/3 - (7/36 \times 0/72) = 5/3 - 5/2992 = 0/0008\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
انجام تقسیم با روش تبدیل به کسر
فصل 3 : اعداد اعشاری
انجام تقسیم با روش تبدیل به کسر
اگر مقسوم علیه تقسیمی عدد اعشاری ،باشد میتوانیم عدد اعشاری را به صورت کسری بنویسیم و با انجام تقسیم کسرها، حاصل تقسیم را به دست آوریم.
مثال
تقسیم های زیر را به روش تبدیل به کسر انجام دهید.
الف\(0/34 \div 1/7\)
\(0/34 \div 1/7 = \frac{{34}}{{100}} \div \frac{{17}}{{10}} = \frac{{34}}{{100}} \times \frac{{10}}{{17}} = \frac{2}{{10}} = 0/2\)
\(4 \div 0/08\) ب
\(4 \div 0/08 = 4 \div \frac{8}{{100}} = \frac{3}{1} \times \frac{{100}}{8} = \frac{{100}}{2} = 50\)
اگر صورت و مخرج کسری را در عددی (غیر از صفر) ضرب کنیم کسر حاصل با کسر اولیه برابر است.
\(\frac{3}{5} = \frac{6}{{10}} = \frac{9}{{15}} = \frac{{12}}{{20}} = \frac{{15}}{{25}} = ....\)
مثال
الف\(\frac{{{{0/34}_{ \times 100}}}}{{{{1/7}_{ \times 100}}}} = \frac{{{{34}_{ \div 17}}}}{{{{170}_{ \div 17}}}} = \frac{2}{{10}}\)
ب\(\frac{{{4_{ \times 100}}}}{{{{0/08}_{ \times 100}}}} = \frac{{400}}{8} = 50\)
ج\(\frac{{{{7/2}_{ \times 100}}}}{{{{0/06}_{ \times 100}}}} = \frac{{720}}{6} = 120\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
مرکز تقارن و تقارن مرکزی
فصل 4 : تقارن و مختصات
تقارن مرکزی
1 تقارن یا قرینه یابی نسبت به یک نقطه را تقارن مرکزی می گویند.
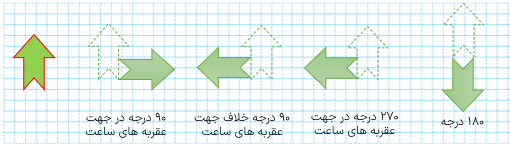
2 در تقارن مرکزی شکل به اندازه ی نیم دور (۱۸۰ درجه) حول (دور) نقطه ی داده شده می چرخد.
مثال
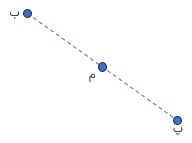
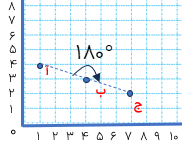
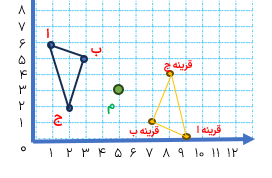
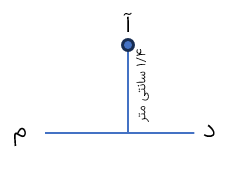
قرینه ی نقطه ی (ب) را نسبت به نقطه ی (م) به صورت زیر است:
با خط کش از نقطه ی «ب» به نقطه ی «م» وصل می کنیم و سپس پاره خط «م ب» را به اندازه ی خودش ادامه می دهیم تا نقطه ی «پ» به دست آید. نقطه ی «پ» قرینه ی نقطه ی «ب» نسبت به نقطه ی «م» است.
در صفحات شطرنجی بدون استفاده از خط کش نیز میتوان قرینه ی یک نقطه را نسبت به نقطه دیگر یافت.
مثال
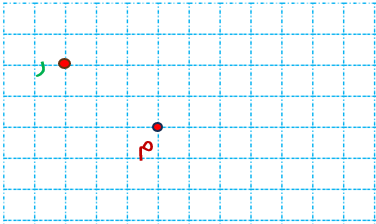
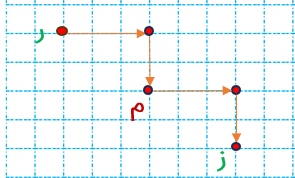
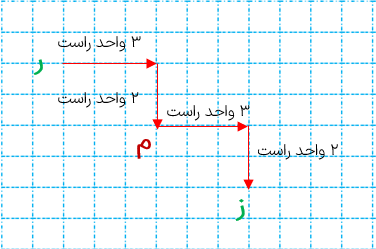
قرینه ی نقطه ی «ر» را نسبت به نقطه ی «م» بیابید.
نقطه ی «ز» قرینه ی نقطه ی «ر» نسبت به نقطه ی «م» است.
مثال
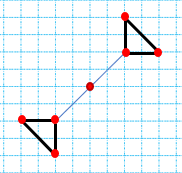
قرینه ی شکل مقابل را نسبت به نقطه ی «م» رسم کنید.
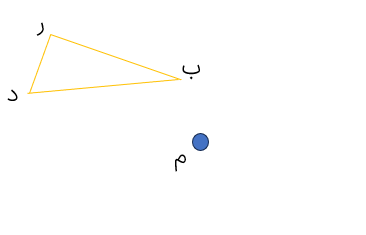
به وسیله ی خط کش قرینه ی هر یک از نقطه های «ز» و «ب» و «د» را نسبت به نقطه ی «م» پیدا کرده و آنها را به هم وصل می کنیم.
اگر نقطه ای مانند م» در داخل یک شکل وجود داشته باشد که قرینه ی هر نقطه روی محیط شکل، نسبت به نقطه ی «م» نقطه ای روی محیط باشد. گوییم نقطه ی «م» مرکز تقارن شکل است.
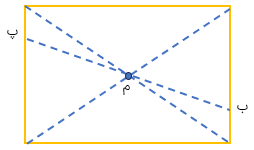
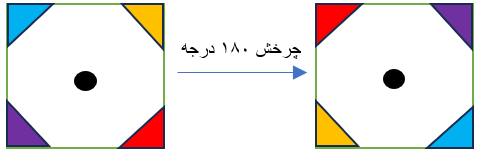
اگر مستطیل را ۱۸۰ درجه حول (دور) نقطه ی «م» بچرخانیم روی خودش منطبق می شود.
نقطه ی برخورد قطرهای مستطیل مرکز تقارن مستطیل است یعنی مستطیل تقارن مرکزی دارد.
در تقارن مرکزی اگر بخواهیم مرکز تقارن یک شکل و قرینه اش را بیابیم باید دو نقطه از شکل را مشخص کنیم و هر نقطه را توسط یک پاره خط به قرینه اش وصل کنیم نقطه ی برخورد دو پاره خط، مرکز تقارن است.
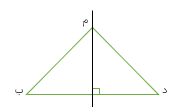
مثال
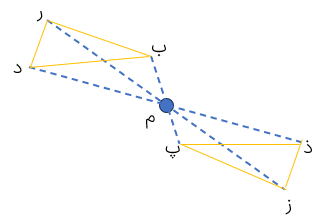
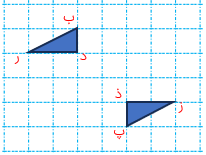
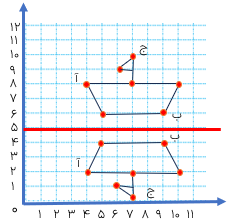
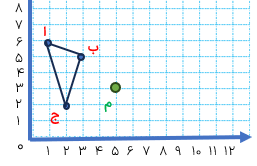
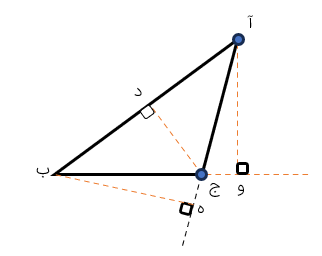
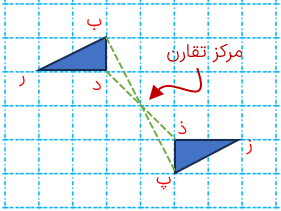
در شکل مقابل مثلث (ب د ر) را ۱۸۰ درجه دوران داده ایم مرکز تقارن را بیابید.
نقطه ی «ب» را به قرینه اش یعنی: نقطه ی «پ» و نقطه ی «د» را به قرینه اش یعنی نقطه «ذ» وصل می کنیم محل برخورد دو پاره خط مرکز تقارن است.
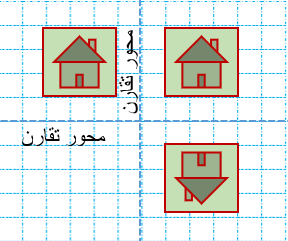
1 اگر شکلی دارای دو خط تقارن محور تقارن عمود برهم ،باشد نقطه ی برخورد دو خط تقارن مرکز تقارن شکل است.
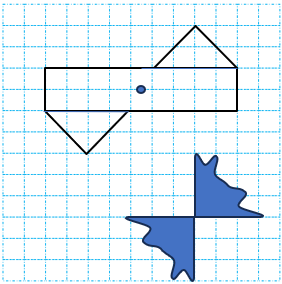
2 بعضی از شکلها خط تقارن محور تقارن ندارند اما مرکز تقارن دارند برای مثال شکل های زیر محور تقارن ندارند اما مرکز تقارن دارند.
یافتن قرینه نقاط مختصاتی
فصل 4 : تقارن و مختصات
یافتن قرینه نقاط مختصاتی
در سال گذشته با تقارن مرکزی آشنا شدید و آموختید که اگر بخواهیم قرینه ی نقطه ای مانند «آ» را نسبت به نقطه ی «م» به دست آوریم ابتدا به وسیله ی خط کش این دو نقطه را به هم وصل می کنیم و در طرف دیگر به همان اندازه ادامه میدهیم تا به قرینه ی «آ» برسیم. اگر بخواهیم قرینه ی یک شکل را نسبت به یک نقطه رسم کنیم میتوانیم از روشهای زیر استفاده کنیم.
۱- استفاده از کاغذ شفاف
در این روش ابتدا کاغذ شفاف را روی شکل مورد نظر قرار داده و آن شکل را رسم می کنیم، سپس نوک مداد را روی نقطه ای که می خواهیم قرینه ی شکل را نسبت به آن رسم می گذاریم و کاغذ شفاف را ۱۸۰ درجه (نیم دور) حول آن نقطه می چرخانیم به این ترتیب قرینه ی شکل نسبت به نقطه رسم می شود.
2- جابه جایی نقاط شکل
برای رسم قرینه ی یک شکل نسبت به یک نقطه ابتدا قرینه ی رأس های آن شکل را نسبت به نقطه ی مورد نظر مشخص می کنیم نقاط به دست آمده را مانند شکل اصلی به یک دیگر وصل میکنیم برای مشخص کردن قرینه ی هر رأس کافی است که آن رأس را به وسیله خط کش به نقطه ی مورد نظر وصل کنیم و در طرف دیگر آن نقطه به همان اندازه امتداد دهیم.
3- استفاده از محور تقارن
ابتدا روی نقطه ی مورد نظر یک محور افقی و یک محور عمودی رسم میکنیم سپس قرینه ی شکل را ابتدا نسبت به محور عمودی رسم می کنیم تا شکل (۱) به دست آید و بعد قرینه ی شکل (۱) را نسبت به محور افقی رسم میکنیم تا شکل (۲) که همان قرینه ی شکل اصلی نسبت به نقطه ی «م» می باشد، به دست آید.
۴- انتقال نقاط روی صفحه ی شطرنجی:
در این روش باید جابه جایی هر رأس را تا نقطه ی مورد نظر، ابتدا به صورت افقی و سپس عمودی بررسی کنیم سپس از آن نقطه مجدداً به همان جهت قبلی ابتدا افقی و سپس عمودی حرکت کنیم به این ترتیب قرینه ی هر رأس نسبت به نقطه ی مورد نظر مشخص می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مرکز تقارن و محور تقارن
فصل 4 : تقارن و مختصات
مرکز تقارن
وقتی شکلی به اندازه ی ۱۸۰ درجه (نیم دور) حول نقطه ای بچرخد و روی خودش منطبق شود، می گوییم شکل مرکز تقارن دارد با توجه به شکلهای زیر که در آنها هر شکل را ۱۸۰ درجه حول نقطه ی مشخص شده دوران داده ایم. نتیجه می شود که مربع مستطیل و متوازی الاضلاع دارای مرکز تقارن هستند، اما مثلث و ذوزنقه مرکز تقارن ندارند.
در متوازی الاضلاع مربع مستطیل و لوزی محل برخورد قطرها همان مرکز تقارن است.
دقت داشته باشید اگر شکل زیر را ۱۸۰ درجه حول نقطه ی م بچرخانیم با توجه به این که رنگ های شکل اصلی جابه جا می شوند پس نقطه ی «م» نمی تواند مرکز تقارن شکل باشد.
چون رنگ های شکل های زیر برهم منطبق نمی شوند این شکل مرکز تقارن ندارد.
یادآوری محور تقارن
محور تقارن خطی است که شکل را به دو قسمت مساوی تقسیم می کند به طوری که اگر شکل را از روی آن خط تا کنیم، آن دو قسمت کاملاً بر هم منطبق شوند.
به خط تقارن هر شکل دقت کنید:
متوازی الاضلاع مثلث مختلف الاضلاع و تمامی ذوزنقه ها به غیر از ذوزنقه متساوی الساقین، محور تقارن ندارند.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
دوران
فصل 4 : تقارن و مختصات
دوران
در دوران (چرخش) غیر از ۱۸۰ درجه و ۳۶۰ درجه حتما باید جهت دوران مشخص شود که در جهت عقربه های ساعت است و یا در خلاف جهت عقربه های ساعت.
مثال
در صفحه ی شطرنجی ،زیر شکل «الف» را با دورانها مشخص شده ی زیر رسم کنید.
۱ ۹۰ درجه در جهت عقربه های ساعت
۲ ۹۰ درجه در جهت خلاف عقربه های ساعت
۳ ۲۷۰ درجه در جهت عقربه های ساعت
۴ ۱۸۰ درجه
1 دوران ۲۷۰ درجه در جهت عقربههای ،ساعت با دوران ۹۰ درجه در جهت خلاف عقربه های ساعت یکسان است.
2 اگر شکلی را حول یک نقطه به اندازه ی ۱۸۰ درجه یا کم تر بچرخانیم و شکل روی خودش قرار گیرد، می گوییم شکل دارای تقارن چرخشی است.
مثال
شکل مقابل تقارن چرخشی دارد، زیرا با دوران ۹۰ درجه حول نقطه ی «م» روی خودش قرار می گیرد.
مثال
شکل مقابل نیز دارای تقارن چرخشی است زیرا با دوران ۶۰ درجه حول نقطه ی «م»، روی خودش قرار می گیرد.
تقارن چرخشی
فصل 4 : تقارن و مختصات
تقارن چرخشی
وقتی شکلی را حول یک نقطه به اندازه ی ۱۸۰ درجه یا کم تر در جهت حرکت عقربه های ساعت بچرخانیم و شکل روی خودش منطبق شود میگوییم ،شکل تقارن چرخشی دارد به شکل های زیر دقت کنید.
چون این شکل بعد از ۹۰ درجه چرخش در جهت حرکت عقربه های ساعت دوباره روی خودش منطبق می شود، پس دوران چرخشی دارد.
چون این شکل بعد از ۱۸۰ درجه چرخش در جهت حرکت عقربههای ساعت دوباره روی خودش منطبق می شود پس دوران چرخشی دارد.
اگر شکل زیر را از ۱ تا ۱۸۰ درجه بچرخانیم هیچ گاه برخودش منطبق نمی شود لذا این شکل دوران چرخشی ندارد.
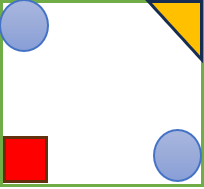
شکل زیر تقارن چرخشی دارد.
شکل زیر تقارن چرخشی ندارد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
محورهای مختصات
فصل 4 : تقارن و مختصات
محورهای مختصات
صفحهی مختصات از دو محور عمودی و افقی تشکیل شده است که به محور افقی، محور طول و به محور عمودی، محور عرض میگویند با توجه به تقسیم بندی روی این دو محور مکان هر نقطه روی صفحه را می توانیم تعیین کنیم که به آن مختصات نقطه می گویند.
مختصات نقطه را به صورت\(\left[ \begin{array}{l} \times \\ + \end{array} \right]\) نمایش می دهیم که عدد × را مؤلفه ی افقی (طول) نقطه و عدد + را مؤلفه ی عمودی (عرض) نقطه می گویند.
مؤلفه ی افقی در بالا و مؤلفه ی عمودی باید در پایین مختصات یک نقطه نوشته شود.
مثال
مختصات نقطه های زیر را با استفاده از صفحه ی مختصات مقابل بنویسید.
\(1 = \left[ \begin{array}{l}3\\6\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,2 = \left[ \begin{array}{l}0\\5\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3 = \left[ \begin{array}{l}3\\2\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4 = \left[ \begin{array}{l}6\\5\end{array} \right]\)
نقطه ی «م» که ابتدا مشترک دو محور ر است، دارای مختصات \(\left[ \begin{array}{l}0\\0\end{array} \right]\) است . و مختصات هر نقطه در صفحه مختصات، نسبت به این نقطه حساب می شود.
در صفحه ی مختصات مقابل، هر یک از رأس های مثلث (ب ر ح) را ۲ واحد به راست و ۳ واحد به بالا حرکت داده ایم تا مثلث(پ ز ج) به دست آید به این کار انتقال می گوییم.
ب=\(\left[ \begin{array}{l}2\\3\end{array} \right]\mathop \to \limits_{ + 3}^{ + 2} \left[ \begin{array}{l}4\\5\end{array} \right]\)
ح=\(\left[ \begin{array}{l}1\\1\end{array} \right]\mathop \to \limits_{ + 3}^{ + 2} \left[ \begin{array}{l}3\\4\end{array} \right]\)
ر=\(\left[ \begin{array}{l}2\\1\end{array} \right]\mathop \to \limits_{ + 3}^{ + 2} \left[ \begin{array}{l}4\\4\end{array} \right]\)
0صفحه ی ، مختصات زیر، مختصات سه رأس \( = \left[ \begin{array}{l}1\\1\end{array} \right]\) د , \( = \left[ \begin{array}{l}2\\1\end{array} \right]\) ک و \( = \left[ \begin{array}{l}2\\3\end{array} \right]\) ف از مثلث (د گ ف ) را سه برابر کرده ایم و به ترتیب رأس های از مثلث (ق ذ گ) به دست آمده است. چون مختصات سه برابر شده اند. پس محیط مثلث بدست امده سه برابر محیط مثلث اولی است و مساحت آن ۳ × ۳ یعنی ۹ برابر مساحت مثلث اول است.
ما معمولاً در زندگی روزمره از نقشه ها در پیدا کردن موقعیت ها و مکان هایی که شناخت کافی از آن ها نداریم، استفاده می کنیم هرنقطه روی نقشه با عددهایی مشخص میشود که در اصطلاح «مختصات» آن نقطه می گوییم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
مختصات نقطه
فصل 4 : تقارن و مختصات
مختصات نقطه
مکان همه ی نقطه های موجود در یک صفحه را میتوانیم به کمک دو محور عمود برهم که در اصطلاح «محور مختصات» گفته می شود مشخص کنیم صفحه ی مختصات از دو محور عمود برهم که یکی از آن ها محور افقی (طول ها) و دیگری محور عمودی (عرض ها) میباشد تشکیل شده است. هر دو در نقطه ی صفر (مبدأ) مشترک هستند به دو عددی که با آن مکان نقطه را در صفحه تعیین میکنیم، مختصات آن نقطه می گوییم.
به صفحه مختصات زیر توجه کنید:
در صفحه ی مختصات زیر اگر از نقطه ی «آ» بر محورهای طول و عرض عمود کنیم، به این ترتیب طول نقطه ی «آ» برابر ۳ و عرض آن برابر ۵ می باشد. لذا نختصات این نقطه را به صورت \( = \left[ \begin{array}{l}3\\5\end{array} \right]\) آ می نویسیم و می خوانیم نقطه ی «آ» به طول3 و عرض ۵ همچنین مختصات نقاط دیگر هم برابر است با:
ج=\(\left[ \begin{array}{l}5\\3\end{array} \right]\)
ب=\(\left[ \begin{array}{l}6\\1\end{array} \right]\)
د=\(\left[ \begin{array}{l}0\\7\end{array} \right]\)
ه=\(\left[ \begin{array}{l}8\\0\end{array} \right]\)
همان طور که ملاحظه مي کنید، با توجه به نقاط آ و ج ، با جابه جا شدن طول و عرض هر نقطه جای نقطه در صفحه و در نتیجه مختصات آن تغییر می کند.
نقطه ی ه روی محور افقی یا همان محور طول ها قرار دارد. از طرفی عرض این نقطه برابر صفر است، پس هر نقطه که روی محور طول ها قرار داشته باشد، عرضش صفر است.
نقطه ی د روی محور عمودی یا همان محور عرض ها قرار دارد از طرفی طول این نقطه برابر صفر است پس هر نقطه که روی محور عرض ها قرار داشته باشد، طولش صفر است.
تعیین مختصات نقاط
برای تعیین مختصات هر نقطه توانیم از مبدأ مختصات شروع به حرکت افقی و سپس حرکت عمودی می کنیم تا به نقطه ی مورد نظر برسیم. سپس در قسمت بالای مختصات باید مقدار حرکت در جهت افقی و در قسمت پایین آن هم مقدار حرکت در جهت عمودی را بنویسیم.
در صفحه ی مختصات مقابل اگر از مبدأ ۴ واحد به سمت راست و سپس واحد به سمت بالا حرکت کنیم به نقطه ی «و» می رسیم. پس:
مختصات نقطه ی «و» برابر\(\left[ \begin{array}{l}4\\3\end{array} \right]\) می باشد.
نمایش نقطه در صفحه ی مختصات
برای نمایش نقطه ای که مختصات آن معلوم است کافی است که از مبدأ مختصات ابتدا به اندازه ی عدد داده شده برای طول به صورت افقی و پس از آن به اندازه ی عدد داده شده برای عرض، به صورت عمودی حرکت کنیم تا به نقطه ی مورد نظر برسیم.
برای نمایش نقطه ی (\(\left[ \begin{array}{l}5\\4\end{array} \right]\) م) کافی است که از مبدأ ابتدا به اندازه ی ۵ واحد به صورت افقی و به سمت راست و پس از آن به اندازه ی ۴ واحد به صورت عمودی و به سمت بالا حرکت کنیم تا به نقطه ی «م» برسیم.
رسم شکل های هندسی در صفحه مختصات
فصل 4 : تقارن و مختصات
رسم شکل های هندسی در صفحه مختصات
اگر مختصات رأس های یک شکل هندسی معلوم ،باشد میتوانیم این رأس ها را در صفحه ی مختصات به طور دقیق مشخص نماییم، سپس آن نقاط را به وسیله ی خط کش به یک دیگر وصل می کنیم تا شکل مورد نظر رسم شود. حالا با شمردن تعداد مربع های داخل شکل یا استفاده از فرمول های محاسبه ی مساحت، می توانیم مساحت شکل مورد نظر را تعیین کنیم.
مثال
نقاط \( = \left[ \begin{array}{l}2\\1\end{array} \right]\) آ \( = \left[ \begin{array}{l}5\\1\end{array} \right]\) ب \( = \left[ \begin{array}{l}5\\4\end{array} \right]\) ج رأس های یک مثلث هستند. ابتدا مثلث را رسم کرده، سپس مساحت آن را حساب کنید.
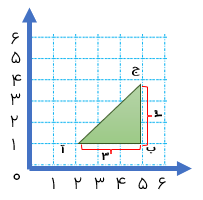
ابتدا نقاط بالا را به طور دقیق روی صفحه ی مختصات مشخص و آنها را به یک دیگر وصل میکنیم تا مثلث آب ج» به دست آید. همان طور که ملاحظه میکنید این مثلث قائم الزاویه است، پس مساحت آن برابر است با
۴/۵ = ۲ ÷ (۳×۳) = ۲ ÷ (قاعده × ارتفاع) = مساحت مثلث
بزرگ نمایی شکل ها در صفحه مختصات
به مختصات رأس های دو مستطیل «آ ب ج د» و «ا ز و ه» دقت کنید.
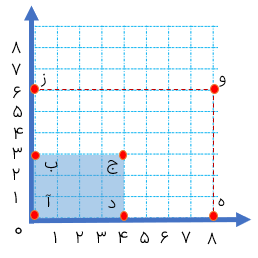
مستطیل «آ ز و ه» :
آ=\(\left[ \begin{array}{l}0\\0\end{array} \right]\) ب=\(\left[ \begin{array}{l}0\\3\end{array} \right]\) ج=\(\left[ \begin{array}{l}4\\3\end{array} \right]\) د=\(\left[ \begin{array}{l}4\\0\end{array} \right]\) آ=\(\left[ \begin{array}{l}0\\0\end{array} \right]\) ز=\(\left[ \begin{array}{l}0\\6\end{array} \right]\)
همان طور که ملاحظه کنید، ابعاد مستطیل بزرگ تر دو برابر ابعاد مستطیل کوچک تر است، اما مساحت آن ۴ برابر مساحت مستطیل کوچک تر می باشد.
۴۸ = ۶ × ۸ = مساحت مستطیل بزرگ
۱۲ = ۳ × ۴ = مساحت مستطیل کوچک تر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
انتقال شکل در صفحه ی مختصات
فصل 4 : تقارن و مختصات
انتقال شکل در صفحه ی مختصات
اگر در صفحه ی مختصات نقطه ای را جابه جا کنیم یک انتقال انجام داده ایم. به طور مثال اگر از نقطه ای مانند \(\left[ \begin{array}{l}1\\5\end{array} \right]\) = آ سه واحد به سمت راست و سپس دو واحد به سمت پایین حرکت کنیم به نقطه ی \(\left[ \begin{array}{l}4\\3\end{array} \right]\) = ب می رسیم به این ترتیب می گوییم که نقطه ی «آ» را به نقطه «ب» منتقل کرده ایم.
برای انتقال یک شکل در صفحه ی مختصات کافی است که ابتدا تمامی رأسها را به اندازه ی خواسته شده انتقال دهیم سپس نقاط به دست آمده را مانند شکل اولیه به یک دیگر وصل کنیم. به این ترتیب شکلی به دست می آید که با شکل اولیه مساوی است ولی در صفحه جابه جا شده است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
تقارن و مختصات
فصل 4 : تقارن و مختصات
تقارن و مختصات
مثال قرینه ی نقطه\(\left[ \begin{array}{l}2\\7\end{array} \right]\) = ب نسبت به خط تقارن قرمز، نقطه ی \(\left[ \begin{array}{l}6\\7\end{array} \right]\) =ث است و قرینه ی نقطه ی «ب» نسبت به خط تقارن آبی، نقطه ی \(\left[ \begin{array}{l}2\\1\end{array} \right]\) = پ است.
دو نقطه ی «ب» و «ت» دارای مؤلفه های عمودی برابرند.
دو نقطه ی «ب» و «پ» دارای مؤلفه های افقی برابرند.
مؤلفه ی عمودی (عرض) هر نقطه و قرینه اش نسبت به یک خط عمودی با هم برابرند. مؤلفه ی افقی (طول) هر نقطه و قرینه اش نسبت به یک خط افقی با هم برابرند.
قرینه ی یک نقطه نسبت به خط تقارن عمودی
می دانیم که برای مشخص کردن قرینه ی یک نقطه نسبت به یک خط تقارن کافی است که از آن نقطه بر خط تقارن عمود کنیم و در طرف دیگر خط به همان اندازه پیش برویم در شکل مقابل نقطه ج=\(\left[ \begin{array}{l}6\\4\end{array} \right]\) قرینه ی نقطه ی ى آ=\(\left[ \begin{array}{l}2\\4\end{array} \right]\) نسبت به خط تقارن (ه و ) است همان طور که ملاحظه می کنید، عرض این دو نقطه با هم برابر است و خط تقارن دقیقا از نقاطی به طول ۴ (میانگین ۲ و ۶) عبور می کند.
قرینه ی یک نقطه نسبت به خط تقارن افقی
در محور مختصات زیر شکل۲(شکل پایین) قرینه ی شکل ۱ (شکل بالا) نسبت به خط تقارن افقی است.
همان طور که ملاحظه می کنید طول هر نقطه و قرینه ی آن نسبت به خط تقارن با هم برابر است.
آ= \(\left[ \begin{array}{l}4\\8\end{array} \right]\) و قرینه آ برابر=\(\left[ \begin{array}{l}4\\2\end{array} \right]\)
ب= \(\left[ \begin{array}{l}9\\6\end{array} \right]\) و قرینه ب برابر=\(\left[ \begin{array}{l}9\\4\end{array} \right]\)
ج= \(\left[ \begin{array}{l}7\\10\end{array} \right]\) و قرینه ج برابر=\(\left[ \begin{array}{l}7\\0\end{array} \right]\)
در دو نقطه که نسبت به یک خط تقارن افقی قرینه هستند طول ها ،برابر ولی عرضها متفاوت هستند.
قرینه ی یک نقطه نسبت به یک نقطه در صفحه مختصات
برای پیدا کردن قرینه ی یک نقطه نسبت به نقطه ی دیگر در صفحه ی مختصات می توانیم از روش های زیر استفاده کنیم
۱- جابه جایی:
برای جابه جا شدن از نقطه ی \(1 = \left[ \begin{array}{l}1\\4\end{array} \right]\) به نقطه ی \(2 = \left[ \begin{array}{l}4\\3\end{array} \right]\) ، ابتدا باید به صورت افقی و به سمت راست ۳ واحد سپس به صورت عمودی و به سمت پایین یک واحد حرکت کنیم. حالا برای پیدا کردن قرینه ی «1»نسبت به نقطه ی «2» همین عمل را انجام می دهیم، یعنی از نقطه ی «2»ابتدا ۳ واحد افقی به سمت راست و سپس یک واحد عمودی به سمت پایین حرکت می کنیم تا به نقطه ی \(3 = \left[ \begin{array}{l}7\\2\end{array} \right]\) برسیم.
2- تقارن مرکزی:
از نقطه ی «1» به نقطه ی «2» وصل می کنیم و به همان اندازه در طرف دیگر نقطه ی «2» پیش می رویم: تا به نقطه ی «3» برسیم.
3- دوران ۱۸۰ درجه:
اگر نقطه ی «آ» را به اندازه ی ۱۸۰ درجه نسبت به نقطه ی م دوران دهیم (بچرخانیم)، به نقطه ی «ج» می رسیم.
برای رسم قرینه ی یک شکل نسبت به یک نقطه ابتدا باید قرینه ی تمامی رأس های شکل را با استفاده از یکی از روش های بالا (روش تقارن مرکزی ساده تر است) نسبت به نقطه ی داده شده مشخص کنیم. سپس نقاط مشخص شده را مانند شکل اصلی به یک دیگر وصل کنیم
مثال
قرینه ی مثلث مقابل را نسبت به مرکز تقارن «م» رسم کنید سپس مختصات رأس های قرینه ی آن را بنویسید.
روش اول ابتدا با استفاده از تقارن ،مرکزی قرینه ی هر یک از نقاط «آ»، «ب» و «ج» را نسبت به نقطه ی «م» مشخص میکنیم سپس مختصات آن ها را می نویسیم.
ا=\(\left[ \begin{array}{l}1\\6\end{array} \right]\) و قرینه ا=\(\left[ \begin{array}{l}9\\0\end{array} \right]\)
ب=\(\left[ \begin{array}{l}3\\5\end{array} \right]\) و قرینه ب=\(\left[ \begin{array}{l}7\\1\end{array} \right]\)
ج=\(\left[ \begin{array}{l}2\\2\end{array} \right]\) و قرینه ج=\(\left[ \begin{array}{l}8\\4\end{array} \right]\)
حالا نقاط به دست آمده را در محور مختصات مشخص، و مثل شکل اصلی به یک دیگر وصل می کنیم تا شکل مانند شکل روش قبل شود.
طول و سطح
فصل 5 : اندازه گیری
طول و سطح
می دانیم که برای اندازه گیری مقداری از هر چیز نیاز به واحد داریم برای مثال برای اندازه گیری قد یک انسان از واحد متر یا سانتی متر و برای اندازه گیری سنگینی یک جسم از واحد گرم یا کیلوگرم استفاده می کنیم. معنی کلمات زیر را یاد بگیرید:
كيلو یعنی هزار : مثال: کیلوگرم یعنی هزار گرم - کیلومتر یعنی هزار متر.
دسی یعنی یک دهم: مثال: دسی متر یعنی یک دهم متر.
سانتی یعنی یک صدم : مثال: سانتی متر یعنی یک صدم متر.
میلی یعنی یک هزارم: مثال: میلی متر یعنی یک هزارم متر - میلی گرم یعنی یک هزارم گرم - میلی لیتر یعنی یک هزارم لیتر که معادل یک سی سی یا یک سانتی متر مکعب است.
در جدول زیر واحدهایی را که به طور معمول از آنها استفاده می کنیم، بیان شده است:
تبدیل واحدهای طول
با استفاده از جدول زیر به راحتی میتوان واحدهای طول را تبدیل کرد.
مثال
۳/۴ متر، چند سانتی متر است؟
با استفاده از جدول می دانیم که هر متر ۱۰۰ سانتی متر است و برای تبدیل از واحد بزرگ (متر) به واحد کوچک (سانتی متر) باید از عمل ضرب استفاده کنیم.
سانتی متر ۳۴۰ = ۱۰۰ × ۳/۴
روش دیگر تبدیل واحدها استفاده از جدول تناسب است.
مثال
۱۷ متر چند کیلومتر است؟
برای تبدیل واحدها از روش زیر استفاده می کنیم.
یعنی برای تبدیل واحد بزرگ به واحد کوچک از عمل ضرب و برای تبدیل واحد کوچک به واحد بزرگ از عمل تقسیم استفاده می شود.
مثال
یک کیلومتر چند سانتی متر است؟
(واحد کیلومتر از واحد سانتی متر بزرگ تر است.)
یعنی یک کیلومتر ۱۰۰۰00 سانتی متر است.
مثال
۰/۰۱۶ کیلومتر یعنی چند سانتی متر؟
سانتی متر ۱۶۰۰ = ۱۰۰۰۰۰ × ۰/۰۱۶
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
واحدهای سطح (مساحت)
فصل 5 : اندازه گیری
واحدهای سطح (مساحت)
می دانیم که مساحت مربع برابر است با یک ضلع ضرب در خودش.
اگر مربعی به ضلع یک سانتی متر داشته باشیم مساحت آن برابر است با ۱ سانتی متر مربع.
۱ سانتی متر مربع : ۱ سانتی متر × ۱ سانتی متر = مساحت مربع
اگر مربعی به ضلع یک متر داشته باشیم مساحت آن برابر است با ۱ متر مربع.
دسی متر مربع : دسی متر × ۱۰ دسی متر = ۱ متر × ۱ متر = ۱ متر مربع
دسی متر مربع ۱۰۰ = ۱ متر مربع
سانتی متر مربع: ۱۰۰۰۰ = ۱۰۰ سانتی متر × ۱۰۰ سانتی متر = ۱ متر × ۱ متر = ۱ متر مربع
سانتی متر مربع ۱۰۰۰۰=۱ متر مربع
میلی متر مربع: ۱۰۰۰۰ = ۱۰۰۰ میلی متر × ۱۰۰۰ میلی متر = ۱ متر × ۱ متر = ۱ متر مربع
میلی متر مربع ۱۰۰۰۰۰۰ = 1متر مربع
سانتی متر مربع: ۱۰۰ = ۱۰ سانتی متر × ۱۰ سانتی متر = ۱ دسی متر × ۱ دسی متر= ۱ دسی متر مربع
سانتی متر مربع ۱۰۰=۱ دسی متر مربع
میلی متر مربع: ۱۰۰۰۰ = ۱۰۰ میلی متر × ۱۰۰ میلی متر = ۱ دسی متر × ۱ دسی متر =۱ دسی متر مربع
میلی متر مربع ۱۰۰۰۰=۱ دسی متر مربع
برای اندازه گیری مساحت مزرعه ها پارک ها و جنگل ها از واحد بزرگ تری به نام هکتار استفاده می شود.
یک هکتار مساحت مربعی است که اندازه ی هر ضلع آن ۱۰۰ متر است.
متر مربع ۱۰۰۰۰=۱ هکتار\( \Rightarrow \) متر مربع 10000 = 100 متر × 100 متر = 1 هکتار
برای اندازه گیری سطح های بزرگ تر مانند مساحت شهرها کشورها قاره ها و اقیانوس ها از واحد بزرگ تری به نام کیلومتر مربع استفاده میشود یک کیلومتر مربع مساحت مربعی است که اندازه ی هر ضلع آن یک کیلومتر یا ۱۰۰۰ متر است.
مساحت مربع شکل مقابل یک کیلومتر مربع است و مساحت مربعی که در بالا سمت راست رنگ شده، یک هکتار است.
متر مربع ۱۰۰۰۰۰۰ = ۱۰۰۰ متر × ۱۰۰۰ متر= ۱ کیلومتر ×۱ کیلومتر = ۱ کیلو متر مربع
متر مربع ۱۰۰۰۰۰۰ = ۱ کیلومتر مربع
تبدیل واحد
برای تبدیل واحدها دو روش وجود دارد:
۱- استفاده از ضرب و تقسیم
2- استفاده از تناسب
مثال
۲/۳ متر مربع چند سانتی متر مربع است؟
استفاده از ضرب و تقسیم
سانتی متر مربع ۲۳۰۰۰ = ۱۰۰۰۰ × ۲/۳\( \Rightarrow \) سانتی متر مربع 10000 = 1 متر مربع
استفاده از تناسب
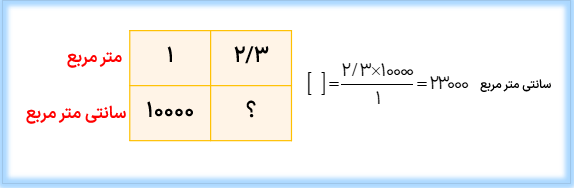
تبدیل واحدهای سطح
کیلومتر مربع مساحت مربعی به ضلع یک کیلومتر است از طرفی چون هر کیلومتر، برابر ۱۰۰۰ متر است بنابراین ۱ کیلومتر مربع، برابر ۱۰۰۰ × ۱۰۰۰ یعنی ۱۰۰۰۰۰۰ متر مربع می باشد. از واحد کیلومتر مربع برای بیان مساحت سطح های بزرگ مانند مساحت قاره،ها کشورها و شهرها استفاده می شود.
یک هکتار مساحت مربعی به ضلع ۱۰۰ متر است. پس هر هکتار برابر ۱۰۰ × ۱۰۰ یعنی ۱۰۰۰۰ متر مربع می باشد.
از واحد هکتار برای بیان مساحت زمین های کشاورزی و جنگل ها استفاده می شود.
هر کیلومتر مربع برابر ۱۰۰ هکتار است.
یک متر مربع مساحت مربعی به ضلع ۱ متر است. از طرفی چون هر دسی متر، برابر ۰/۱ متر است پس هر دسی متر مربع برابر ۰/۱ متر است.پس هر دسی متر مربع برابر 1/0×1/0 یعنی 0/01 متر مربع می باشد .از این واحد هم برای بیان مساحت اتاق ها استفاده می شود.
به طور مثال مساحت یک اتاق ۱۲ متر مربع و ۶ دسی متر مربع میباشد. که این مساحت با ۱۲/۰۶ متر مربع برابر است.
یک سانتی متر مربع مساحت مربعی به ضلع ۱ سانتی متر است. از طرفی چون هر سانتی متر، برابر ۰/۰۱ متر است، پس هر سانتی متر برابر ۰/۱۰/۰۱ یعنی ۰/۰۰۰۱ متر مربع میباشد. از این واحد برای بیان مساحت سطح های کوچک مانند سطح کتاب استفاده می شود.
پیشنهاد میشود که از الگوی زیر برای تبدیل واحدهای سطح به یک دیگر و با کمک از جدول تناسب استفاده کنید.
مثال
الف ۲۵۶ متر مربع، چند هکتار است؟
می دانیم که هر ۱۰۰۰۰ متر مربع برابر یک هکتار است بنابراین:
ب ۲۵۶ هکتار چند متر مربع است؟
از آن جا که هر هکتار برابر ۱۰۰۰۰ متر مربع است پس ۲۵۶ هکتار را برابر ۱۰۰۰۰ × ۲۵۶ یعنی ۲۵۶۰۰۰۰ متر مربع می باشد.
ج ۳۵۴ دسی متر مربع چند سانتی متر مربع است؟
می دانیم که هر دسی متر برابر ۱۰ سانتی متر است، پس با توجه به رابطه های زیر هر دسی متر مربع برابر۱۰۰ سانتی متر مربع است.
۱۰۰ سانتی متر مربع = ۱۰ سانتی متر × ۱۰ سانتی متر و ۱ دسی متر مربع = ۱ دسی متر × ۱ دسی متر
سانتی متر مربع ۳۵۴۰۰ = ۱۰۰ × ۳۵۴ = ۳۵۴ دسی متر مربع
د ۷۸۹ هکتار چند کیلومتر مربع است؟ میدانیم که هر ۱۰۰ هکتار برابر یک کیلومتر مربع است، بنابراین:
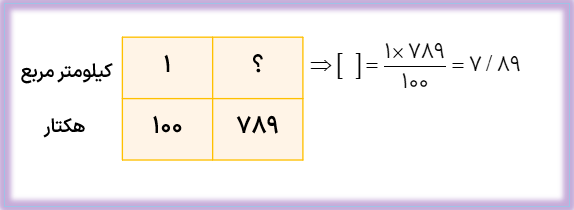
مثال
اگر مستطیل مقابل نقشه ی یک زمین فوتبال باشد و هر یک سانتی متر روی شکل برابر ۲۵ متر بر روی زمین باشد، به سؤالات زیر پاسخ دهید.
الف مساحت کل این زمین فوتبال چند متر است؟
با توجه به این که هر یک سانتی متر روی نقشه معادل ۲۵ متر در طبیعت (واقعیت) است پس طول و عرض زمین برابر است با:
متر ۱۰۰= ۴×۲۵ = طول زمین ، متر ۷۵ = ۲۵ × ۳ = عرض زمین
متر مربع ۷۵۰۰ = ۷۵ × ۱۰۰ = مساحت زمین فوتبال
ب مساحت نیمه ی زمین فوتبال چند هکتار است؟
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
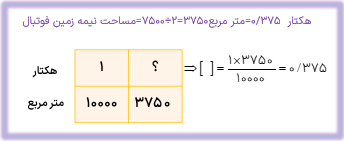
واحدهای طول
فصل 5 : اندازه گیری
واحدهای طول
در سال ها قبل با مفهوم اندازه گیری و واحدهای مختلف برای اندازه گیری مواردی از قبیل طول سطح و حجم و ... آشنا شدید. در این قسمت بعضی از واحدهای اندازه گری را یادآوری می کنیم:
واحد اندازه گیری طول: کیلومتر – متر - دسی متر – سانتی متر – میلی متر
واحدهای اندازه گیری زمان: سال - ماه - هفته - روز – ساعت – دقیقه – ثانیه
واحدهای اندازه گیری جرم (وزن): تن – کیلوگرم - گرم
واحدهای اندازه گیری سطح: کیلومتر مربع - هکتار - متر مربع - دسی متر مربع - سانتی متر مربع – میلی متر مربع
واحدهای اندازه گیری: حجم متر مکعب – دسی متر مکعب – سانتی متر مکعب
واحدهای اندازه گیری گنجانش: لیتر – میلی لیتر
واحدهای اندازه گیری زاویه: درجه
همان طور که میدانید برای اندازه گیری در هر یک از موارد بالا باید از واحد مناسب آن استفاده کنیم به طور مثال برای اندازه گیری طول یک اتاق بهتر است از واحد متر استفاده کنیم اما برای اندازه گیری فاصله ی بین دو شهر بهتر است از واحد کیلومتر و برای اندازه گیری ضخامت یک کتاب از واحد میلی متر استفاده کنیم.
پس انتخاب واحد مناسب در اندازه گیری از اهمیت زیادی برخوردار است. حال اگر در انتخاب واحدها دقت نکنیم، مجبوریم از عددهای خیلی بزرگ و یا خیلی کوچک استفاده کنیم به طور مثال فاصله ی تهران تا مشهد تقریبا ۹۰۰ کیلومتر است این فاصله با واحد متر برابر ۹۰۰,۰۰۰ متر و با واحد سانتی متر برابر ۹۰,۰۰۰,۰۰۰ سانتی متر است.
تبدیل واحدهای طول
هر کیلومتر، برابر ۱۰۰۰ متر است.
(۱متر) × ۱۰۰۰ = ۱
هر متر برابر ۱۰ دسی متر است.
(1دسی متر) × ۱۰ = ۱
هر دسی متر برابر ۱۰ سانتی متر است.
(1 سانتی متر) × ۱۰ = ۱ دسی
هر سانتی متر، برابر ۱۰ میلی متر است.
(1 میلی متر) × ۱۰ = ۱ سانتی متر
پیشنهاد میکنیم که از الگوی زیر برای تبدیل واحدهای طول به یک دیگر استفاده کنید. همچنین می توانید از جدول تناسب هم در تبدیل واحدهای طول به یک دیگر استفاده کنید.
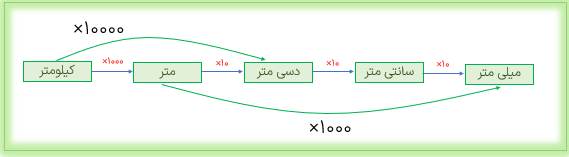
مثال
الف ۴۳۲ کیلومتر چند متر است؟
می دانیم که هر کیلومتر برابر ۱۰۰۰ متر است. پس ۴۳۲ کیلومتر برابر ۱۰۰۰ × ۴۳۲ یعنی ۴۳۲۰۰۰ متر است.
ب ۵۲۷ متر چند کیلومتر است؟ میدانیم که هر کیلومتر برابر ۱۰۰۰ متر است، بنابراین:
ج ۵۲۷ دسی متر چند کیلومتر است؟
طبق الگوی بالا هر کیلومتر، برابر ۱۰ × ۱۰۰۰ ۱۰۰۰۰ دسی متر است بنابراین:
د ۳۷ دسی متر چند میلی متر است؟
طبق الگوی بالا هر دسی متر برابر ۱۰ × ۱۰ یعنی ۱۰۰ میلی متر است، پس ۳۷ دسی متر برابر ۱۰۰ × ۳۷ یعنی ۳۷۰۰ میلی متر است.
حجم و جرم
فصل 5 : اندازه گیری
حجم و جرم
به شکل مقابل هرم می گویند.
قاعده ی هرم یک چندضلعی است (مانند: مثلث، مربع مستطیل، پنج ضلعی و ...)
به هر یک از سطح های تشکیل دهندهی هرم یک وجه می گویند.
گسترده ی هرم بالا به صورت مقابل است.
اگر گسترده هرم از چهار مثلث متساوی الاضلاع هم اندازه تشکیل شده باشد به آن چهاروجهی منتظم هم گفته می شود.
شکل زیر یک مکعب و گسترده ی آن را نشان می دهد.
ضلع ضلع x ضلع = حجم مکعب
ضلع × ضلع ×۶ = مساحت گسترده ی مکعب (مساحت کل مکعب)
همه ی ضلع های مکعب با هم برابرند.
برای اندازه گیری ،حجم واحدهایی مانند مترمکعب دسی مترمکعب (لیتر) و سانتی مترمکعب (سی سی) وجود دارد.
یک متر مکعب، حجم مکعبی است که اندازه ی هر ضلع آن یک متر باشد.
یک دسی مترمکعب (یا یک لیتر)، حجم مکعبی است که اندازه ی هر ضلع آن یک دسی متر یا ۱۰ سانتی متر باشد. این واحد برای اندازه گیری حجم مایعات بسیار مورد استفاده قرار می گیرد.
۱ لیتر یا یک دسی متر مکعب = حجم
یک سانتی متر مکعب حجم مکعبی است که اندازه ی هر ضلع آن یک سانتی متر باشد. نام های دیگر این واحد سی سی» و «میلی لیتر» است.
۱ سانتی متر مکعب = حجم
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
واحدهای حجم
فصل 5 : اندازه گیری
واحدهای حجم
دسی متر مکعب 1000=۱۰ دسی متر× ۱۰ دسی متر × ۱۰ دسی متر = ۱ متر × ۱ متر × ۱ متر = ۱ متر مکعب
لیتر ۱۰۰۰ = دسی متر مکعب ۱۰۰۰=۱ متر مکعب
سانتی متر مکعب ۱۰۰۰۰۰۰ = ۱۰۰ سانتی متر × ۱۰۰ سانتی متر × ۱۰۰ سانتی متر= ۱ متر× ۱ متر ×۱ متر = ۱ متر مکعب
میلی لیتر ۱۰۰۰۰۰۰ = سی سی ۱۰۰۰۰۰ = سانتی متر مکعب ۱۰۰۰۰۰۰=۱ متر مکعب
سانتی متر مکعب ۱۰۰۰ = ۱۰ سانتی متر × ۱۰ سانتی متر × ۱۰ سانتی متر = ۱ دسی متر× ۱ سی متر× ۱ دسی متر = ۱ دسی متر مکعب = ۱ لیتر
میلی لیتر ۱۰۰۰ = سی سی ۱۰۰۰ =سانتی متر مکعب ۱۰۰۰=۱ دسی متر مکعب = ۱ لیتر
برای تبدیل واحدهای حجم میتوان از دو روش ضرب و جدول تناسب استفاده کرد.
مثال
۳/۲ متر مکعب برابر چند لیتر است؟
روش ۱: میدانیم که هر متر مکعب مساوی ۱۰۰۰ لیتر است؛ پس
لیتر ۳۲۰۰ = ۱۰۰۰ × ۳/۲
روش ۲: استفاده از جدول تناسب
مثال
حجم و مساحت گسترده ی مکعبی به ضلع ۵ سانتی متر را حساب کنید.
سانتی متر مکعب ۱۲۵ = ۵ ×۵ × ۵ = حجم
سانتی متر مربع ۱۵۰ = ۵ × ۵ × ۶ = مساحت گسترده (مساحت کل)
شکل زیر یک مکعب مستطیل و گسترده ی آن را نشان میدهد اضلاع برابر در گسترده ی شکل مشخص شده اند.
در گسترده ی مکعب مستطیل سطح هایی (وجه) هایی که هم رنگ هستند دارای مساحت های مساوی هستند. این سطح ها در مکعب مستطیل در مقابل هم قرار می گیرند.
اگر اضلاع مکعب مستطیل را به صورت مقابل نام گذاری کنیم حجم و مساحت گسترده ی مساحت کل آن به صورت زیر محاسبه می شود.
ارتفاع × عرض × طول = حجم مکعب مستطیل
(ارتفاع × عرض) + (ارتفاع × طول) + (عرض × طول ) × ۲ = مساحت گسترده ی مکعب مستطیل (مساحت کل)
مثال
شکل مقابل گسترده ی یک مکعب مستطیل است با توجه به اندازه های روی آن، حجم و مساحت گسترده ی مکعب مستطیل را حساب کنید.
سانتی متر مکعب ۱۲۰ = ۳×۸×۵ = حجم
سانتی متر مربع ۱۵۸ = (۵×۳) + (3×8)+ (۸×۵)× ۲ = مساحت گسترده (مساحت کل)
شکل مقابل یک مخروط است. مخروط شبیه هرم است فقط قاعده ی آن به شکل دایره است (چند ضلعی نیست).
شکل مقابل یک کره است.
توپ فوتبال به شکل یک کره است کره را از هر طرف نگاه کنیم، یک دایره می بینیم.
شکل مقابل یک استوانه است.
استوانه ی مقابل را اگر از بالا نگاه کنیم یک دایره می بینیم و اگر از راست یا روبه رو نگاه کنیم یک مستطیل می بینیم.
دو تصویر مختلف از این استوانه
واحدهای اندازه گیری :جرم واحدهای معمول اندازه گیری جرم از کوچک به بزرگ عبارت اند از:
میلی گرم - گرم - کیلوگرم - تن
جدول مقابل رابطه ی بین این واحدها را نشان می دهد.
واحد میلی گرم واحد بسیار کوچکی است و به طور معمول در صنایع داروسازی مورد استفاده قرار می گیرد.
یعنی هر ۱ تن مساوی ۱۰۰۰۰۰۰ گرم است.
جرم یک سی سی آب تقریبا یک گرم است و چون یک لیتر مساوی ۱۰۰۰ سی سی است، بنابراین جرم یک لیتر آب معادل ۱۰۰۰ گرم یا یک کیلوگرم است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
هرم و مکعب
فصل 5 : اندازه گیری
هرم
هرم یک شکل فضایی (چندوجهی) است که همه ی وجه های آن به جز یکی از آن ها در یک رأس مشترک هستند. به شکل های زیر دقت کنید.
مكعب
مکعب یک شکل فضایی شش وجهی است که تمامی وجههای آن از مربع های برابر هستند. هر مکعب دارای گوشته (رأس) و ۱۲ لبه (ضلع) است.
اندازه ی لبه (ضلع) را سه مرتبه نوشته و در هم ضرب کنید = حجم مکعب
مساحت یک مربع × ۶ = مساحت یک وجه × ۶ = مساحت گسترده ی مکعب
مثال
یک مکعب به صورت مقابل است حجم و مساحت گسترده ی این مکعب چه قدر است؟
سانتی متر مکعب ۱۲۵ = ۵ ×۵× ۵ = حجم
سانتی متر مربع ۱۵۰ = ۶×۲۵ = (۵×۵) ×۶ = مساحت گسترده
مکعب مستطیل
مکعب مستطیل یک شکل فضایی شش وجهی است که تمامی وجه های آن به شکل مستطیل هستند. هر مکعب مستطیل دارای ۸ گوشه (رأس) و ۱۲ لبه (ضلع) است. شکل های زیر چند حالت گسترده ی مکعب مستطیل را نمایش می دهند.
ارتفاع × عرض × طول = حجم مکعب مستطیل
(ارتفاع × عرض) + (ارتفاع × طول) + (عرض × طول) × ۲ = مساحت گسترده ی مکعب مستطیل
مثال
حجم و مساحت گستردهی مکعب مستطیل مقابل را به دست آورید.
سانتی متر مکعب ۱۲۰ = ۸×۳×۵ = حجم
سانتی متر مربع ۱۵۸ = (15×40×24)×2= (۳×۵) + (۸×۵) + (۸×۳)]× ۲ = مساحت گسترده
معرفی چند شکل هندسی دیگر
معرفی و تبدیل واحدهای حجم
فصل 5 : اندازه گیری
معرفی و تبدیل واحدهای حجم
یک متر مکعب اگر مکعبی به ضلع یک متر داشته باشیم حجم آن یک متر مکعب می باشد.
۱ متر × ۱ متر ×1 متر × ۱ متر = ۱ متر مکعب
یک دسی متر مکعب اگر مکعبی به ضلع یک دسی متر داشته باشیم حجم آن یک دسی متر مکعب می باشد.
یک سانتی متر مکعب اگر مکعبی به ضلع یک سانتی متر داشته باشیم حجم آن یک سانتی متر مکعب می باشد.
هر متر برابر ۱۰ دسی متر است پس:
۱۰۰۰ دسی متر مکعب = ۱۰ دسی متر × ۱۰ دسی متر × ۱۰ دسی متر = ۱ متر مکعب
هر متر برابر ۱۰۰ سانتی متر است پس:
۱۰۰۰۰۰۰ سانتی متر مکعب = ۱۰۰ سانتی متر × ۱۰۰ سانتی متر × ۱۰۰ سانتی متر = ۱ متر مکعب
۱ هر سانتی متر مکعب برابر یک سی سی است.
۲ هر دسی متر مکعب برابر یک لیتر است پس هر لیتر برابر ۱۰۰۰ سی سی می باشد.
3 هر متر مکعب برابر ۱۰۰ لیتر است.
مثال
مخزنی داریم به شکل مکعب مستطیل و به ابعاد ۱ متر، ۵ دسی متر و ۳۰ سانتی متر، حجم این مخزن چند دسی متر مکعب است؟ در این مخزن چند لیتر آب میتوان ریخت؟
ابتدا بهتر است تمامی واحدها را به دسی متر تبدیل کنیم:
۳ دسی متر = ۳۰ سانتی متر = ارتفاع مکعب مستطیل
۱۰ دسی متر = ۱ متر = طول مکعب مستطیل
دسی متر مکعب ۱۵۰ = ۳ × ۵ × ۱۰ = حجم مکعب مستطیل
می دانیم که هر دسی متر مکعب با ۱ لیتر برابر است پس گنجایش این مخزن همان ۱۵۰ لیتر است.
تبدیل واحدهای جرم
تن: هر هزار کیلوگرم برابر یک تن است. پس یک کیلوگرم برابر \(\frac{1}{{1000}}\) تن می باشد.
کیلوگرم: هر کیلوگرم برابر ۱۰۰۰ گرم است. پس یک گرم برابر \(\frac{1}{{1000}}\) کیلوگرم می باشد.
گرم: هر گرم برابر ۱۰۰۰ میلی گرم است. پس هر میلی گرم برابر \(\frac{1}{{1000}}\)گرم است.
برای تبدیل واحدهای جرم میتوان از الگوی زیر استفاده کرد:
مثال
الف ۸۳۵۴ کیلوگرم چند تن است؟
ب ۵۴۹ میلی گرم چند کیلوگرم است؟
مساحت دایره
شکل مقابل یک دایره را نشان می دهد.
نقطه ی «م» مرکز دایره است.
پاره خط «م س» شعاع دایره است.
پاره خط «ف ب» قطر دایره است.
دایره دارای بی شمار شعاع و بی شمار قطر است.
شعاع های دایره با هم برابر و قطرهای دایره نیز با هم برابرند.
اندازه ی هر قطر دو برابر شعاع است یعنی اندازه ی شعاع نصف قطر است.
۳/۱۴ × قطر = محیط دایره
۳/۱۴ × شعاع × شعاع = مساحت دایره
عدد ۳/۱۴ را عدد پی می.گویند البته این عدد مقدار تقریبی عدد پی است.
محیط (ه ر ) شکل یعنی دوتا دور شکل یعنی طول خطی که دو شکل را تشکیل می دهد.
مثال
در شکل های زیر محیط هر شکل با خط قرمز مشخص شده است.
می دانیم که یک دایره کامل یک زاویه ی ۳۶۰ درجه را نشان میدهد. اکنون به شکل های زیر که در آن ها دایره ها به قسمتهای مساوی تقسیم شدهاند و اندازه ی زاویه های هر بخش دقت کنید.
مثال
محیط و مساحت نیم دایره ی شکل مقابل را حساب کنید.
مساحت دایره ی کامل:
۱۰ × ۱۰ × ۳/۱۴ =314 سانتی متر مربع
مساحت نیم دایره:
سانتی متر مربع ۱۵۷ = ۲ ÷ ۳۱۴
اندازه ی قطر (د س) + طول خط منحنی = محیط نیم دایره
. \( = \frac{{2 \times 10 \times 3/14}}{2} = 31/4\)طول خط منحنی
31/4×20=51/4= محیط نیم دایره
مثال
محیط و مساحت شکل مقابل را حساب کنید.
شکل مقابل \(\frac{3}{4}\) یک دایره است.
. \(\frac{3}{4} \times 20 \times 20 \times 3/14 = 3 \times 100 \times 3/14 = 3 \times 31\)=مساحت شکل
.\(2 \times 30 \times 3/14 \times \frac{3}{4} + 2 \times 20 = 94/40 = 134/2\) = محیط شکل
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
دایره و چند شکل مهم دیگر
فصل 5 : اندازه گیری
محیط دایره
در سال های گذشته با محیط دایره و نحوه ی محاسبه ی آن آشنا شدید:
عدد پی × شعاع × ۲ = عدد پی × قطر = محیط دایره
با توجه به رابطه ی بالا نصف محیط دایره برابر است با حاصل ضرب شعاع در عدد بی، اما دقت داشته باشید که محیط یک نیم دایره از رابطه ی زیر به دست می آید.
قطر + (عدد پی × شعاع) =محیط نیم دایره
مساحت دایره
در کتاب درسی چگونگی اثبات رابطهی مساحت دایره بیان شده است و در این جا فقط به بیان این رابطه می پردازیم.
عدد پی × شعاع × شعاع = مساحت دایره
۲ + (عدد پی × شعاع × شعاع) = مساحت نیم دایره
۴ +(عدد پی × شعاع × شعاع) = مساحت ربع دایره
مثال
مساحت هر یک از شکل های زیر را به دست آورید.
الف)
سانتی متر مربع ۷۸/۵ = ۳/۱۴ × ۲۵ = ۳/۱۴ × ۵ × ۵ = مساحت دایره به شعاع ۵ سانتی
ب) دقت داشته باشید که در این نیم دایره اندازه ی قطر داده شده است لذا ابتدا باید اندازه ی شعاع را حساب کنیم:
دسی متر ۴ = ۲ ÷ ۸ = شعاع نیم دایره به قطر ۸ دسی متر
مساحت چند شکل مهم
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
خط و زاویه
فصل 5 : اندازه گیری
خط و زاویه
فاصله ی بین دو نقطه طول پاره خطی است که دو نقطه را به هم وصل می.کند در شکل روبه رو، فاصله ی دو نقطه ی و «س» برابر است با طول پاره خط «ب س».
فاصله ی یک نقطه تا یک خط پاره خط برابر است با طول پاره خط عمودی که از آن نقطه بر خط رسم می شود. در شکل زیر فاصله ی نقطه ی «م» از خط ب پ برابر است با طول پاره خط «م ج».
فاصله ی هر رأس مثلث از ضلع مقابل آن برابر است با : ارتفاع وارد بر آن ضلع
در شکل زیر (ب ج) فاصله ی نقطه ی «ب» از ضلع پت است بنابراین ب ج» ارتفاع وارد بر ضلع (پ ت) است.
از هر نقطه روی یک پاره خط فقط یک خط عمود بر آن می توان رسم کرد.
مثال
از نقطه ی «ج» روی خط «م د» فقط یک خط مانند بس را میتوان بر خط «د م» عمود رسم کرد.
عمود منصف یک پاره خط خطی است که از وسط پاره خط بگذرد و بر آن عمود رسم شود. در شکل مقابل خط «م ل » عمود منصف پاره خط س ده است.
دقت کنید چون هر پاره خط فقط یک نقطه ی وسط دارد بنابراین هر پاره خط فقط یک عمود منصف دارد.
هر نقطه روی عمود منصف پاره خط از دو سر پاره خط به یک فاصله است یعنی در شکل روبه رو اندازه «د م» با «م ب» برابر است.
دقت کنید چون خط و نیم خط اندازه ی مشخصی ندارند بنابراین نقطه ی وسط آن ها نیز مشخص نیست. پس برای نیم خط و خط نمی توان عمود منصف رسم کرد.
فاصله ی دو نقطه از هم
فصل 5 : اندازه گیری
فاصله ی دو نقطه از هم
می دانیم که از دو نقطه شمار خط خمیده میگذرد اما از دو نقطه فقط یک خط راست عبور می کند که به این ترتیب طول پاره خطی که دو نقطه را به یک دیگر وصل میکند برابر فاصله ی بین این دو نقطه است. در شکل زیر طول پاره خط آب برابر فاصله بین دو نقطه ی (آ) و (ب) است.
فاصله ی دو نقطه طول کوتاه ترین پاره خطی است که دو نقطه را به هم وصل می کند.
فاصله ی نقطه از خط
کوتاه ترین فاصله ی یک نقطه تا یک خط برابر طول پاره خطی است که از نقطه ی مورد نظر بر آن خط عمود میشود برای رسم پاره خط عمود از یک نقطه بر یک خط میتوانیم از گونیا استفاده کنیم. در شکل مقابل فاصله ی نقطه ی (آ) از خط (د م) برابر ۱/۴ سانتی متر است.
فاصله ای نقطه از خط طول پاره خطی است که از آن نقطه به خط عمود می شود
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ارتفاع و عمود منصف
فصل 5 : اندازه گیری
رسم ارتفاع در مثلث
اگر در مثلثی از یک رأس بر ضلع مقابل آن عمود کنیم این پاره خط عمود همان ارتفاع مثلث و ضلع مقابل به آن نیز قاعده ی نظیر آن ارتفاع می باشد.. در شکل زیر از رأس (ج) بر ضلع مقابل آن یعنی ضلع آب پاره خط (ج) (د) را عمود کرده ایم به این ترتیب پاره خط (د ج) همان ارتفاع مثلث ضلع (آ ب) نیز قاعده ی متناظر با آن ارتفاع می باشد. توجه داشته باشید که گاهی مجبوریم ارتفاع وارد بر یک ضلع را در خارج از مثلث . بر امتداد آن ضلع رسم کنیم در شکل زیر پاره خط (آ و) ارتفاع هر مثلث دارای سه ارتفاع میباشد که همگی آنها یک دیگر را در یک نقطه قطع می کنند. در شکل های زیر ارتفاع های سه نوع مثلث را نشان داده ایم به ارتفاع هایی که در بیرون مثلث رسم می شوند ارتفاع خارجی می گوییم.
نظیر ضلع (ج) (ب) میباشد که برا امتداد ضلع (ج ب) عمود شده است و این اتفاق زمانی می افتد که مثلث زاویه ی بزرگ تر از ۹۰ درجه داشته باشد.
عمود منصف
در شکل مقابل خط (ج د) بر پاره خط (آ ب) عمود شده و آن را به دو قسمت مساوی تقسیم کرده است. به این خط یعنی خط (ج د)، عمود منصف پاره خط (ب آ) گفته می شود.
در شکل بالا نقطه ی (ه) روی عمود منصف پاره خط (ب آ) قرار دارد از طرفی فاصله ی دو نقطه (ه آ) با فاصله ی دو نقطه ی (ب ه) برابر است از این خاصیت میتوان برای تشخیص عمود منصف بودن یک خط استفاده کرد.
۱ عمود منصف، خطی است که از وسط پاره خط بگذرد و بر آن عمود باشد.
2 هر نقطه روی عمود منصف یک پاره خط از دو سر آن پاره خط به یک فاصله است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
زوایای مکمل و متمم و متقابل به رأس
فصل 5 : اندازه گیری
انواع زاویه
اندازه ی زاویه ی راست (قائمه)، برابر ۹۰ درجه است.
اندازه ی زاویه نیم صفحه برابر ۱۸۰ درجه است.
اندازه ی زاویه تند از صفر درجه بیشتر و از ۹۰ کم تر است.
اندازه ی زاویه ی باز از ۹۰ درجه بیشتر و از ۱۸۰ درجه کم تر است.
اندازه ی زاویه ی تمام صفحه مساوی ۳۶۰ درجه است.
یعنی:
زاویه ی تمام صفحه > زاویه ی نیم صفحه > زاویه ی باز > زاویه ی راست > زاویه ی تند
دو زاویه ی متمم اگر مجموع دو زاویه ۹۰ درجه باشد آن دو زاویه را متمم گویند.
در شکل مقابل زاویه های ۱ و ۲ متمم اند.
در مثلث قائم الزاویه دو زاویه ی تند متمم یکدیگرند.
مثال
اندازه ی متمم زاویه ی ۲۵ درجه را حساب کنید.
\(90^\circ - 25^\circ = 65^\circ \)
یعنی زاویه ی ۶۵ درجه متمم زاویه ی ۲۵ درجه است.
اگر مجموع دو زاویه ۱۸۰ درجه باشد آن دو زاویه را مکمل می گویند.
در شکل مقابل زاویه های ۱ و ۲ مکمل اند.
مثال
اندازه ی مکمل زاویه ۱۲۰ درجه را حساب کنید.
\(180^\circ - 120^\circ = 60^\circ \)
یعنی زاویه ۶۰ درجه مکمل زاویه ی ۱۲۰ درجه است.
در متوازی الاضلاع زاویه های مجاور مکمل اند، یعنی:
\(\begin{array}{l}1 + 2 = 180^\circ \\\\3 + 4 = 180^\circ \\\\1 + 4 = 180^\circ \\\\2 + 3 = 180^\circ \end{array}\)
مثال
الف اندازه ی زاویه ی متمم و مکمل زاویه ۳۵ درجه را حساب کنید.
مکمل زاویه \(180^\circ - 35^\circ = 145^\circ \)
متمم زاویه \(90^\circ - 35^\circ = 55^\circ \)
ب اختلاف مکمل و متمم این زاویه چند درجه است؟
\(145^\circ - 55^\circ = 90^\circ \)
اختلاف مکمل و متمم هر زاویه ای همیشه ۹۰ است.
اگر دو خط راست یکدیگر را قطع کنند، ۴ زاویه درست میشود که زاویه های روبه رو، دوبه دو متقابل به رأس هستند یعنی در شکل مقابل زاویه های ۱ و ۲ متقابل به رأس هستند. زاویه های ۳ و۴ نیز متقابل به رأس هستند.
دو زاویه ی متقابل به رأس با هم برابرند، یعنی در شکل بالا:
\(\widehat 1 = \widehat 2\,\,\,\,,\,\,\,\,\,\,\widehat 3 = \widehat 4\)
مثال
در شکل مقابل مجموع ۱ و ۲ مساوی ۶۰ درجه است. اندازه ی زاویه ی ۳ چند درجه است؟
.\(\widehat 1,\widehat 2 \to 60^\circ \div 2 = 30^\circ \) اندازه ی
.\(\widehat 3 \to 180^\circ - 30^\circ = 150^\circ \) اندازه ی
دایره ی شکل مقابل به شش قسمت مساوی یا به شش کمان مساوی تقسیم شده است. اگر نقطه های کنار هم روی دایره را به هم وصل کنیم شش پاره خط به وجود آمده نیز مساوی اند یعنی پاره خط های مربوط به کمان های مساوی با هم برابرند.
۱ زاویه ی تند از زاویه راست (قائمه) کوچک تر است.
۲ زاویه ی باز از زاویه ی راست بزرگ تر و از زاویه ی نیم صفحه ۱۸۰( درجه) کوچک تر است.
3 زاویه ی نیم صفحه > زاویه ی باز زاویه ی راست > زاویه ی تند
دو زاویه ی متمم
به هر دو زاویه ای که مجموع آنها ۹۰ درجه باشد دو زاویه متمم میگویند به طور مثال دو زاویه ی ۳۰ درجه و ۶۰ درجه متمم یک دیگر هستند.
مثال
متمم زاویه ۳۷ درجه را حساب کنید.
چون مجموع دو زاویه ی متمم ۹۰ درجه است بنابراین با انجام تفریق زیر میتوانیم زاویه ی ۳۷ درجه را پیدا کنیم.
۵۳ = ۳۷ - ۹۰ = متمم زاویه ۳۷
مثال
دو زاویه ی متمم مشخص کنید که اندازه ی یکی از آن ها ۵ برابر دیگری باشد.
با توجه به این که اندازه ی یکی از زاویه،ها پنج برابر دیگری است لذا در ابتدا باید ۹۰ درجه را به ۶ قسمت مساوی تقسیم کنیم تا اندازه ی زاویه کوچک تر به دست آید.
اندازه ی زاویه کوچک تر ۱۵ = ۶ ÷۹۰
اندازه ی زاویه بزرگ تر ۷۵ = ۵× ۱۵
دو زاویه ی مکمل
به هر دو زاویه که مجموع آن ها ۱۸۰ درجه باشد دو زاویه ی مکمل میگویند به طور مثال دو زاویه ی ۳۰ درجه و ۱۵۰ درجه مکمل یک دیگر هستند.
مثال
مکمل زاویه ی ۳۷ درجه را حساب کنید.
چون مجموع دو زاویه مکمل ۱۸۰ درجه است بنابراین با انجام تفریق زیر میتوانیم مکمل زاویه ی ۳۷ درجه را پیدا کنیم.
۱۴۳ = ۳۷ - ۱۸۰ = مکمل زاویه ی ۳۷
مثال
دو زاویه ی مکمل مشخص کنید که اندازه ی یکی از آن ها پنج برابر دیگری باشد.
چون اندازه ی یکی از زاویه های مکمل پنج برابر دیگری است لذا در ابتدا باید ۱۸۰ درجه را بر ۶ قسمت مساوی تقسیم کنیم تا اندازه ی زاویه ی کوچک تر به دست آید.
۱۵۰ = ۵ × ۳۰ = اندازه ی زاویه بزرگتر و اندازه ی زاویه کوچکتر ۳۰ = ۶ ÷ ۱۸۰
اختلاف متمم و مکمل هر زاویه ای برابر ۹۰ درجه است به طور مثال متمم زاویه ی ۳۰ درجه برابر ۶۰ و مکمل این زاویه برابر ۱۵۰ درجه است و داریم:
150-60=90
دو زاویه ی متقابل به رأس
اگر دو خط هم دیگر را قطع کنند، چهار زاویه به وجود می آید که زاویه های روبه رو دو به دو با هم برابر هستند. به این زاویه ها متقابل به رأس می گویند. توجه داشته باشید که در زاویه های متقابل به رأس، ضلع ها باید در امتداد یک دیگر باشند.
با توجه به این که دو زاویه ی متقابل به رأس باید هم رأس باشند و همچنین اضلاع دو زاویه ی متقابل به رأس باید در امتداد یک دیگر باشد لذا در شکلهای زیر زاویه ی متقابل به رأس وجود ندارد.
مثال
مجموع دو زاویه ی متقابل به رأس ۶۴ درجه است اندازه ی هر یک از آن ها چند درجه است؟
با توجه به این که دو زاویه ی متقابل به رأس با هم برابرند، بنابراین:
۳۲ = ۲ ÷ ۶۴ = اندازه ی هر یک از زاویه ها
مجموع زاویه های داخلی هر مثلث ۱۸۰ درجه است.
مثال
در شکل زیر اندازه ی زاویه ی «م» چند درجه است؟
می دانیم که مجموع همه ی زاویه های داخلی این مثلث باید ۱۸۰ درجه باشد، بنابراین:
۳۵ = ۱۴۵ - ۱۸۰ = (۵۳ + ۹۲) – ۱۸۰= اندازه ی زاویه ی «م»
کسر، نسبت و تناسب
فصل 6 : تناسب و درصد
کسر، نسبت و تناسب
نسبت مقایسه ی بین دو چیز مختلف است. برای مثال اگر نسبت نیمکتها به دانش آموزان در یک کلاس ۱ به ۲ باشد یعنی روی یک نیمکت ۲ نفر مینشینند این نسبت را به صورت زیر در جدول قرار می دهیم و به صورت های «۱ به ۲» یا «۱ و ۲» یا «۲ : ۱» یا \(\frac{1}{2}\)نمایش می دهیم.
مثال
به شکل ها و جدول های زیر توجه کنید.
همان طور که صورت و مخرج کسری را در عددی ضرب میکنیم و کسری مساوی کسر اولیه به دست می آید، اگر نسبت ها را نیز در عددی ضرب کنیم تغییر نمی کنند و نسبت های حاصل با نسبت های اولیه برابرند؛ یعنی نسبت ۲ به ۳ با نسبت ۴ به ۶ برابر است.
مثال
نسبت پول رضا احمد و پرهام مانند \(\frac{5}{6},\frac{2}{3},\frac{1}{2}\) است نسبت ها را به صورت عدد صحیح بیان کنید.
هر سه عدد را در کوچک ترین مخرج مشترک آنها (عدد ۶) ضرب می کنیم.
پرهام:\(\frac{5}{6} \times 6 = 5\)
احمد:\(\frac{2}{3} \times 6 = 4\)
رضا:\(\frac{1}{2} \times 6 = 3\)
یعنی نسبت پول ،رضا احمد و پرهام مانند ۳ به ۴ به ۵ است.
در مسئله های مربوط به نسبت، ترتیب مهم است؛ یعنی وقتی که می گوییم نسبت سن آرش به روزمهر 3به ۵ است یعنی عدد ۳ مربوط به سن آرش و عدد ۵ مربوط به سن روز مهر است.
گاهی نسبت های بین چند مقدار به طور واضح بیان نمیشود که در این صورت باید نسبت بین عامل مشترک آن ها را یکسان کنیم تا بتوانیم نسبت هر یک از عامل های داده شده را تشخیص دهیم.
مثال
نسبت سن پرهام به سعید ۳ به ۵ و نسبت سن سعید به سارا ۲ به ۷ است نسبت سن پرهام به سارا را بیابید.
دقت کنید که در این مسئله نسبت سن پرهام به سارا واضح نیست و سعید در هر دو نسبت مشترک پس باید نسبت سن سعید در هر دو حالت به یک عدد تبدیل شود یعنی نسبت سن پرهام به سارا، مانند ۶ به ۳۵ است.
هرگاه تغییرات دو مقدار به صورتی باشد که نسبت حاصل تقسیم آنها مقدار ثابتی باشد، به آن دو مقدار، مقدارهای متناسب می گوییم.
مثال
نسبت طول یک ضلع مربع به محیط آن، همواره ثابت و مساوی است؛ پس می گوییم طول ضلع یک مربع با محیط آن متناسب است به جدول زیر دقت کنید.
اندازه ی ضلع مربع با مساحت آن متناسب نیست؛ یعنی نسبت آن ثابت نیست.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تناسب
فصل 6 : تناسب و درصد
تناسب
دو نسبت مساوی یک تناسب را تشکیل میدهند حاصل تناسب یعنی یافتن مقدار مجهول در دو نسبت مساوی؛ یعنی اگر یکی از عددها در تناسب مشخص نباشد، مقدار آن را بیابیم.
جدولی که تناسب را نمایش میدهد جدول تناسب نامیده می شود.
مثال
در تساوی مقابل در جای خالی چه عددی را باید قرار داد؟
تناسب را به صورت دو کسر مساوی نیز نشان می دهند.
برای مثال جدول تناسب فوق را به صورت \(\frac{3}{4} = \frac{9}{{12}}\) نیز نشان می دهند.
تسهیم به نسبت یعنی تقسیم کردن به نسبت سهم هر چیزی یا هر کسی از کل سهم. برای مثال وقتی که می گوییم می خواهیم ۵۰ تومان را نسبت ۲ به ۳ بین علی و رضا تقسیم کنیم یعنی می خواهیم این پول را طوری تقسیم کنیم که از ۵ قسمت کل ،پول ۲ قسمت به علی و ۳ قسمت به رضا برسد. این طوری:
مثال
احمد ۲۸ عدد پیچ و مهره دارد. نسبت پیچها به مهرههای او است؛ او چند پیچ و چند مهره دارد؟
عدد ۲۸ نه تعداد پیچ ها است و نه تعداد مهره ها بلکه مجموع تعداد پیچها و مهره ها است، بنابراین باید مجموع نسبت ها را حساب کنیم
یعنی احمد ۸ پیچ و ۲۰ مهره دارد.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
نسبت
فصل 6 : تناسب و درصد
نسبت
اگر بخواهیم در ریاضیات رابطه ی بین دو چیز یا دو عدد را نشان دهیم از نسبت استفاده . می کنیم به طور مثال هر موتورسیکلت دارای دو چرخ است بنابراین دو موتورسیکلت دارای چهار چرخ است و سه موتورسیکلت دارای شش چرخ می باشند به این ترتیب میتوان گفت که نسبت تعداد موتورسیکلت ها به تعداد چرخ ها ۱ به ۲ است که این نسبت را به صورت کسر با - و به صورت اعشاری با ۰/۵ هم نمایش می دهند. البته در بعضی از کتاب ها نسبت ۱ به ۲ را به صورت های (۱و۲) و همچنین (۲و ۱) هم نمایش میدهند. دقت داشته باشید که نسبت را به کسری نخوانید بلکه آن را به صورت (۱ به ۲) و یا (۱ و ۲) بخوانید.
۱ نسبت واحد ندارد اما باید دقت کنیم که در هر نسبت صورت و مخرج را بر حسب یک واحد معین بنویسیم.
2 صورت و مخرج هر نسبت را می توان ساده کرد.
مثال
قد علی ۱۷۵ سانتی متر است و قد مهدی ۱/۵ متر است نسبت قد علی به قد مهدی چه قدر است؟
با توجه به این که قد مهد ی برحسب متر بیان شده است ابتدا قد او را بر حسب سانتی متر بیان می کنیم، چون هر متر معادل صد سانتی متر است پس قد مهدی ۱۵۰ = ۱۰۰ × ۱/۵ سانتی متر می شود. بنابراین؛ در برخی از مسائل صورت یا مخرج و یا هر دوی آنها را به صورت کسری میدهند که برای ساده تر شدن نسبت باید صورت نسبت را بر مخرج آن تقسیم کنیم.
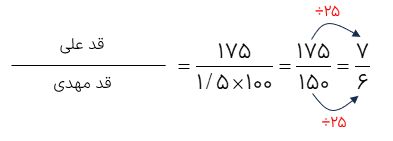
مثال
نسبت سن سارا به سن مینا مثل به است. نسبت سن این دو نفر را به ساده ترین شکل بیان کنید.
نسبت \(\frac{4}{3}\)ساده ترین شکل بیان نسبت سن این دو نفر است.
جدول تناسب
فصل 6 : تناسب و درصد
جدول تناسب
هرگاه دو نسبت با هم مساوی باشند میگوییم که این دو نسبت با هم دیگر متناسب هستند. به طور مثال با توجه به جدول زیر نسبت طول ضلع هر مربع به محیط آن\(\frac{1}{4}\)است و با کم تر یا بیش تر شدن ضلع مربع، محیط هم به همان نسبت تغییر میکند یعنی اگر طول ضلع را دو برابر کنیم محیط هم دو برابر می شود و یا اگر محیط را ۲۰ برابر کنیم طول ضلع هم ۲۰ برابر میشود پس محیط مربع با طول ضلع آن متناسب است و یا به عبارت دیگر طول ضلع مربع با محیط آن تناسب دارد به این جدول که تناسب را نشان می دهد جدول تناسب می گوییم.
در حل برخی مسائل می توانیم از جدول تناسب استفاده کنیم و جواب مسئله را به دست آوریم.
مثال
اگر نسبت ۷ به ۱۱ مانند نسبت جای خالی به ۷۷ باشد داخل دایره چه عددی باید بنویسیم؟
برای حل سؤال از جدول تناسب مقابل استفاده میکنیم چون ۱۱ را هفت برابر کردیم تا حاصل ۷۷ شود پس باید ۷ را هم هفت برابر کنیم، بنابراین؛
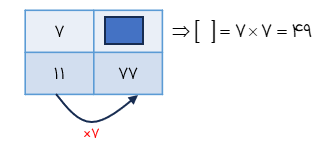
حل جدول تناسب
اگر مانند مثال قبل نتوانیم چند برابر شدن عددها را تشخیص دهیم بهتر است که از روش زیر که به روش طرفين وسطین معروف میباشد کمک بگیریم در جدول مقابل به عددهای ۷ و ۷۷، طرفین و به ۱۱ و هم وسطین گفته . شود. در هر جدول تناسب همواره حاصل ضرب طرفین با حاصل ضرب وسطین برابر است. می بنابراین برای پیدا کردن عدد داخل کافی است که حاصل ضرب طرفین را بر عدد ۱۱ تقسیم کنیم:
تسهیم به نسبت
تسهیم به نسبت یعنی سهیم بودن در نسبت به عبارت دیگر تسهیم به نسبت یعنی مشخص کردن سهم هر چیزی به نسبت معین از کل سهم ها به طور مثال در یک کلاس نسبت دانش آموزانی که به فوتبال علاقه مند هستند به دانش آموزانی که به والیبال علاقه مندند \(\frac{5}{3}\)است پس نسبت دانش آموزانی که به فوتبال علاقه مندند به کل دانش آموزان \(\frac{5}{{5 + 3}} = \frac{5}{8}\) است. همچنین نسبت دانش آموزانی که به والیبال علاقه مندند به کل دانش آموزان \(\frac{3}{{5 + 3}} = \frac{3}{8}\) است. البته به شرط این که این نسبت مربوط به کل دانش آموزان باشد و هر دانش آموز حتما به یکی از این دو ورزش علاقه مند باشد.
مثال
یک نقاش ساختمان برای تهیه ی رنگ سبز هر ۵ کیلوگرم رنگ زرد را با ۳ کیلوگرم رنگ آبی مخلوط میکند. او برای تهیه ۳۲ کیلو گرم رنگ سبز به چند کیلوگرم از هر رنگ نیاز دارد؟
8=3+5 = مجموع نسبت ها
یعنی اگر ۵ کیلوگرم رنگ زرد را با ۳ کیلوگرم رنگ آبی مخلوط کنیم ۸ کیلوگرم رنگ سبز به دست می آید.
مقایسه ی نسبت ها
برای مقایسه چند نسبت ابتدا هر نسبت را به صورت یک کسر می نویسیم و سپس آن ها را مانند مقایسه ی کسرها، از روش مخرج مشترک گیری و یا روشهای دیگر مقایسه می کنیم.
مثال
در ۲ کیلوگرم از یک نوع ،شیرینی ۵۰۰ گرم شکر و در ۳ کیلوگرم از نوع دیگری شیرینی، ۷۰۰ گرم شکر به کار رفته است کدام نوع ،شیرینی شکر بیش تری دارد؟ ابتدا نسبت شکر به شیرینی را در هر دو نوع سپس کسرهای حاصل را با هم مقایسه می کنیم.
با مقایسه \(\frac{{14}}{{60}},\frac{{15}}{{60}}\) نتیجه میشود که شیرینی نوع اول دارای شکر بیش تری است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
درصد
فصل 6 : تناسب و درصد
درصد
نسبت یا کسری که مخرج آن ۱۰۰ باشد، نشان دهنده ی درصد است. برای مثال، کسری \(\frac{{57}}{{100}}\) را به صورت% ۵۷ نشان میدهیم و میخوانیم: پنجاه و هفت درصد
وقتی که میگوییم شیر با چربی ۴% یعنی در هر ۱۰۰ گرم از این شیر ۴ گرم چربی است یا در ۱۰۰ کیلوگرم از این شیر، ۴ کیلوگرم چربی است.
اگر بخواهیم کسری را به صورت درصد بنویسیم باید کسری مساوی با آن و با مخرج ۱۰۰ پیدا کنیم.
\(\frac{3}{5},\frac{1}{4},\frac{{14}}{{25}}\)
مثال
کسرهای مقابل را به صورت درصد بنویسید.
\(\begin{array}{l}\frac{3}{5}\\\\\frac{1}{4}\\\\\frac{{14}}{{25}}\end{array}\)
\(\begin{array}{l}\frac{3}{5} = \frac{{60}}{{100}} = 60\% \\\\\frac{1}{4} = \frac{{25}}{{100}} = 25\% \\\\\frac{{14}}{{25}} = \frac{{56}}{{100}} = 56\% \end{array}\)
اگر بخواهیم کسری را به صورت درصد بنویسیم اما نتوانیم مخرج آن را به سادگی با ضرب کردن در یک عدد به ۱۰۰ تبدیل کنیم ابتدا صورت کسر را بر مخرجش تقسیم کرده و به صورت عدد اعشاری و سپس به شکل درصد می نویسیم.
مثال
کسر\(\frac{3}{8}\)را به صورت درصد بنویسید.
مخرج کسر باید ۱۰۰ باشد تا بتوانیم به صورت درصد بنویسیم.
\(\frac{3}{8} = 3 \div 8 = 0/375 = \frac{{375}}{{1000}} = \frac{{37/5}}{{100}} = 37/5\% \)
مثال
کسر\(\frac{{147}}{{500}}\) را به صورت درصد بنویسید.
توجه کنید که مخرج کسر باید ۱۰۰ باشد تا بتوانیم به صورت درصد بنویسیم.
\(\frac{{147}}{{500}} = \frac{{294}}{{1000}} = \frac{{29/4}}{{100}} = 29/4\% \)
کسرها یا عددهای بزرگ تر از واحد را نیز میتوان به صورت درصد نوشت به مثال های زیر دقت کنید.
مثال
عددهای مقابل را به صورت درصد بنویسید.
\(\frac{7}{5},3/4\)
\(\begin{array}{l}\frac{7}{5} = \frac{{140}}{{100}} = 140\% \\\\3/4 = 3/40 = 340\% \end{array}\)
دقت کنید: ۵/۷۶یعنی ۵۷۶%، ۲/۳ یعنی ۲/۳۰ یعنی ۲۳۰%.
دقت کنید:
دو برابر یعنی %۲۰۰, سه برابر یعنی %۳۰۰ ، هفت برابر یعنی ٪۷۰۰.
کل هر چیزی را ٪۱۰۰. در نظر میگیریم یعنی وقتی می گوییم کل دانش آموزان یک کلاس به اردو می روند، یعنی ۱۰۰% دانش آموزان یک کلاس به اردو میروند یا وقتی میگوییم مبلغ کالایی ۷۰۰۰ تومان است، یعنی ۱۰۰٪ مبلغ کالا ۷۰۰۰ تومان است.
مثال
%۳۰ دانش آموزان کلاسی به مسابقه ی فوتبال رفته اند چند درصد به مسابقه ی فوتبال نرفته اند؟
کل دانش آموزان کلاس ۱۰۰% است.
به مسابقه ی فوتبال نرفته اند ۷۰% = %۳۰ – ۱۰۰%
مثال
فروشنده ای برای فروش کالایش ۲۰% تخفیف می دهد، یعنی چند درصد آن را باید بپردازیم؟
کل مبلغ کالا %۱۰۰ است.
باید بپردازیم ۸۰% = %۲۰ – ۱۰۰%
توجه کنید که ۲۰% مبلغ کالا را تخفیف میدهد یعنی ۲۰% قیمت کالا گرفته نمی شود.
مثال
به شکل (الف) که به ۲۵ قسمت مساوی تقسیم شده است دقت کنید در این شکل ۷ قسمت رنگ شده است، پس\(\frac{7}{{25}}\) شکل (الف) رنگی است. حال اگر همان شکل را به ۱۰۰ قسمت مساوی تقسیم کنیم و به همان اندازه مانند شکل (الف) رنگ کنیم ملاحظه کنید که\(\frac{{28}}{{100}}\) شکل (ب) رنگ شده است این دو کسر نمایش مختلفی از یک چیز هستند در ضمن می توانیم\(\frac{{28}}{{100}}\) را به صورت ۲۸% (میخوانیم ۲۸ درصد) هم نمایش دهیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
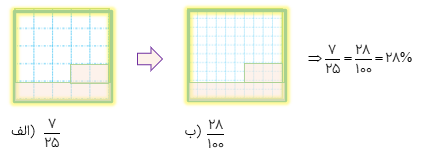
نمایش درصد روی یک شکل
فصل 6 : تناسب و درصد
نمایش درصد روی یک شکل
نسبتی که مخرج آن عدد ۱۰۰ باشد درصد نامیده می.شود به طور مثال اگر در نوعی گز (سوغاتی اصفهان) ۳۵ گرم از هر ۱۰۰ گرم پسته باشد در اصطلاح به آن گز ۳۵ درصد و یا ٪۳۵ گفته می شود.
۱ در صورتی که کسری بزرگ تر از واحد ،باشد درصد آن بیش تر از ۱۰۰ خواهد شد.
۲ مقایسه ی درصد از مقایسه ی کسرها ساده تر است.
از درصد برای درک بهتر از نسبت ها و یا کسرها استفاده میکنیم به این ترتیب که آن نسبت و یا کسر را به صورت کسری با مخرج ۱۰۰ تبدیل میکنیم و سپس آن را به صورت درصد مینویسیم. به طور مثال کسر\(\frac{3}{{30}}\) را می توان به صورت\(\frac{{3 \times 5}}{{20 \times 5}} = \frac{{15}}{{100}}\) یعنی ۱۵% نشان دهیم. بنابراین برای تبدیل و نمایش هر عدد کسری به شکل درصد کافی است که کسری مساوی با آن کسر با مخرج ۱۰۰ پیدا کنیم. حال اگر در یک کسر نتوانیم کسر مساوی با مخرج ۱۰۰ پیدا کنیم. حال اگر در یک کسر نتوانیم کسر مساوی با مخرج ۱۰۰ پیدا کنیم است که تقسیم صورت بر مخرج کسر را تا دو رقم اعشار حساب کنیم و درصد آن عدد را به صورت تقریبی به دست بیاوریم. مثلا در کسر\(\frac{5}{7}\):
\(\frac{5}{7} = 5 \div 7 \to 0/714285714 \simeq 0/71 = \frac{{71}}{{100}} = 71\% \)
نمایش درصد روی یک شکل
برای نمایش هر درصدی روی یک شکل ابتدا درصد را به شکل کسری نوشته و آن را تا جای ممکن ساده می کنیم به این ترتیب به کسری میرسیم که با نمایش آن روی شکل داده شده درصد آن نیز مشخص می شود. به طور مثال اگر بخواهیم ۳۵ درصد یک مستطیل را نشان دهیم ابتدا ۳۵% را به صورت\(\frac{{35}}{{100}}\) می نویسیم و آن را ساده می کنیم تا به کسر\(\frac{7}{{20}}\) برسیم حالا این کسر را روی یک مستطیل نشان می دهیم.
برای حل مسئله های درصد میتوانیم از جدول تناسب استفاده کنیم به مثالهای زیر دقت کنید.
مثال
در یک کارگاه تولید قطعات اتومبیل ۴ درصد از محصولات معیوب هستند. اگر در این کارگاه و در یک روز ۵۵۰ قطعه تولید شود چند تا از قطعات معیوب هستند؟
كل قطعات تولید شده (یعنی ۵۵۰) را به عنوان ۱۰۰. در نظر گرفته و با کمک جدول تناسب جواب را به دست می آوریم.
مثال
برای تهیه ی نوعی دارو سه ماده ی شیمیایی را به نسبت ۵، ۴ و ۱ مخلوط می کنند. در داروی به دست آمده چند درصد از هر نوع ماده وجود دارد؟ در هر ۸۰ گرم از این دارو چند گرم از هر ماده وجود دارد؟
برای حل سؤال از جدول تناسب زیر استفاده مي کنیم:
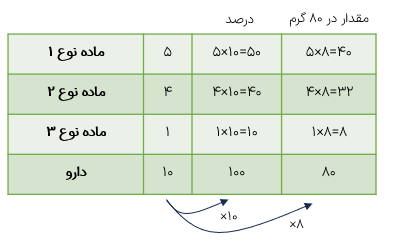
مثال
عددی را هفت برابر کرده ایم.
الف عدد جدید چند درصد عدد اولیه است؟
ب عدد اولیه چند درصد افزایش پیدا کرده است؟
افزایش ۶۰۰% = %۱۰۰ – ۷۰۰%
کاربرد درصد در محاسبات مالی
فصل 6 : تناسب و درصد
کاربرد درصد در محاسبات مالی
در محاسبات مالی همیشه درصد قیمت اصلی کالا یا قیمت اولیه ۱۰۰% در نظر گرفته می شود درصد مالیات و درصد سود همیشه به درصد قیمت اصلی کالا اضافه میشوند و قیمت کالا را افزایش می دهند.
مثال
قیمت کالایی ۲۰۰۰۰ تومان است. اگر ۵ مالیات بر این کالا تعلق بگیرد خریدار برای خرید این کالا چند تومان باید بپردازد؟
قیمت کالا با مالیات ۲۱۰۰۰ تومان است.
مثال
فروشنده ای کالایی را به قیمت ۵۰۰۰ تومان خرید اگر او کالا را با ۳۰% سود قیمت گذاری کند، قیمت فروش کالا چند تومان است؟
قیمت فروش کالا ۶۵۰۰ تومان است.
درصد تخفیف همواره از درصد قیمت اصلی (یعنی ۱۰۰%) کم میشود و قیمت کالا را کاهش می دهد.
مثال
فروشنده ای کتابی را با ۱۰% تخفیف میفروشد. اگر قیمت اولیهی کالا ۴۸۰۰ تومان باشد، خریدار برای خرید این کالا چند تومان باید بپردازد؟
قیمت کالا پس از تخفیف ۴۳۲۰ تومان است.
سال گذشته قیمت کالایی ۴۰۰۰ تومان بوده و امسال همان کالا ۱۰۰۰۰ تومان شده است. قیمت این کالا چند درصد افزایش داشته است؟
درصد افزایش قیمت %۱۵۰ = %۱۰۰ – ۲۵۰%
تخفیف
منظور از تخفیف روی یک کالا این است که مبلغی از کل قیمت کالا را پرداخت نکنیم به طور مثال اگر قیمت کالایی ۵۰۰۰ تومان باشد و آن را با ۱۵% تخفیف خریداری کنیم آن گاه باید مبلغ ۴۲۵۰ تومان را جهت خرید این کالا پرداخت کنیم به روشهای زیر برای محاسبه ی این مبلغ دقت کنید.
روش اول
با استفاده از جدول تناسب ۱۵ قیمت کالا را حساب کنیم و عدد حاصل را از قیمت اصلی کم کنیم.
روش دوم
۱۵% از ۱۰۰% را تخفیف میگیریم پس %۸۵ = %۱۵ – ۱۰۰% از قیمت این کالا را پرداخت می کنیم از طرفی ۸۵% همان ۰/۸۵ است، بنابراین:
در بعضی از مسئله ها مقدار تخفیف و مبلغ پرداختی مشخص است و میخواهند قیمت اولیه را مشخص کنیم. به مثال زیر دقت کنید.
مثال
قیمت کالایی پس از تخفیف ۲۰ درصدی، ۵۶۰۰ تومان شده است قیمت اولیه این کالا چه قدر بوده است؟
روش اول
وقتی %۲۰ از قیمت کالا را تخفیف گرفته ایم یعنی %۸۰ = ۲۰% - %۱۰۰ قیمت آن را پرداخت کرده ایم، 5600 تومان همان ۸۰% قیمت کل است. بنابراین برای تعیین قیمت اولیه یا کل از جدول تناسب زیر کمک می گیریم:
روش دوم
همان طور که گفتیم %۸۰ همان ۵۶۰۰ تومان است از طرفی ۸۰% همان ۰/۸ می باشد، بنابراین:
در بعضی از مسئله ها قیمت اولیه و مبلغ پرداختی مشخص است و میخواهند تا مقدار تخفیف را مشخص کنیم به مثال زیر دقت کنید.
مثال
قیمت کالایی ۸۰۰۰ تومان بود اما فروشنده آن را به مبلغ ۷۲۰۰ تومان فروخت. او چند درصد تخفیف داده است؟
فروشنده ۷۲۰۰ - ۸۰۰۰ یعنی مبلغ ۸۰۰ تومان تخفیف داده است. لذا با استفاده از جدول تناسب زیر درصد تخفیف را مشخص می کنیم:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
سود
فصل 6 : تناسب و درصد
سود
منظور از سود در فروش یک کالا این است که مبلغی بیش تر از قیمت خریداری شده توسط خودمان دریافت کنیم. به طور مثال اگر کالایی را به قیمت ۵۰۰۰ تومان خریداری کنیم و بخواهیم آن را با ۱۵ درصد سود بفروشیم آن گاه باید قیمت این کالا را ۵۷۵۰ تومان اعلام کنیم به روشهای زیر برای محاسبه ی مقدار سود دقت کنید.
روش اول
باید ۱۵ درصد به قیمت کل (یعنی ۱۰۰ درصد) اضافه کنیم بنابراین باید ۱۱۵ = ۱۵ + ۱۰۰ درصد قیمت کالا را دریافت کنیم.
البته می توانیم قیمت فروش کالا را با جمع مقدار سود و مبلغ خریداری شده هم مشخص کنیم:
۵۰۰۰ + ۷۵۰ = ۵۷۵۰
روش دوم
۱۵٪ سود روی %۱۰۰ قیمت خریداری شده توسط خودمان گرفته ایم پس باید ٪۱۱۵ = ٪۱۵ + ٪۱۰۰ یا همان ۱/۱۵ قیمت خریداری شده را دریافت کنیم، بنابراین:
در بعضی از مسئله ها مقدار سود و مبلغ فروش مشخص است و میخواهند مبلغ خرید کالا را مشخص کنیم. به مثال زیر دقت کنید.
مثال
قیمت کالایی پس از افزودن ۲۰ به قیمت آن مبلغ . ۵۷۰۰ تومان اعلام شده است. قیمت خرید این کالا چه قدر بوده است؟
روش اول
وقتی %۲۰ به قیمت کالایی اضافه کرده ایم یعنی ۱۲۰% = %۲۰ + ۱۰۰% قیمت خریداری شده را برای فروش کالا اعلام کرده ایم پس ۵۷۰۰ تومان همان ۱۲۰% قیمت کالا است بنابراین برای تعیین قیمت خرید کالا از جدول تناسب زیر استفاده می کنیم:
البته برای حل این مسئله نیازی به رسم جدول تناسب سه طبقه نیست و بهتر ا است طبقه ی سود را در این جدول حذف کنیم اما این روش را با توجه به کتاب درسی بیان کرده ایم.
روش دوم
همان طور که گفتیم ۵۷۰۰ تومان یعنی ۱۲۰% قیمت خریداری شده از طرفی %۱۲۰ برابر\(\frac{{120}}{{100}}\) یا ۱/۲ است. با تقسیم ۵۷۰۰ بر \(\frac{{120}}{{100}}\) و یا ۱/۲ قیمت خرید مشخص می شود.
.\(5700 \div \frac{{120}}{{100}} = 5700 \times \frac{{100}}{{120}} = 4750 \) = قیمت خرید
در بعضی از مسئله ها قیمت خرید و قیمت فروش کالا را اعلام میکنند و میخواهند تا درصد سود را مشخص کنیم. به مثال زیر دقت کنید.
مثال
علی کالایی را به قیمت ۵۰۰۰ تومان خرید و آن را به قیمت ۶۰۰۰ تومان فروخت، او چند درصد سود کرده است؟
۵۰۰۰ تومان همان ۱۰۰ درصد قیمت خرید است از طرفی علی ۵۰۰۰ – ۶۰۰۰ یعنی مبلغ ۱۰۰۰ تومان سود کرده است لذا با استفاده از جدول تناسب زیر درصد سود او را مشخص می کنیم:
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
مالیات
فصل 6 : تناسب و درصد
مالیات
در کشور عزیزمان به بیشتر کالاها و خدماتی که ارائه میشود مالیات بر ارزش افزوده تعلق می گیرد. در واقع مالیات پولی است که باید به قیمت کالا اضافه شود و از مشتریان دریافت گردد و فروشنده باید این مبلغ اضافه را به خزانه ی دولت واریز نماید و حق ندارد آن را برای خودش بردارد به طور مثال اگر قیمت کالایی ۱۵۰۰۰ تومان باشد و به این کالا %۹ مالیات بر ارزش افزوده تعلق بگیرد باید مبلغ ۱۶۳۵۰ تومان به فروشنده پرداخت کنیم مسئله های مالیات را همانند مسئله های سود حل میکنیم به روش های محاسبه ی مقدار مالیات و مبلغ پرداختی در مثال بالا دقت کنید.
روش اول
روش دوم
%۹ مقدار مالیات بر ارزش افزوده این کالا است پس فروشنده باید 100%+9%=109% یا همان\(\frac{{109}}{{100}}\) قیمت کالا را دریافت کند بنابراین:
.\( = 15000 \times \frac{{109}}{{100}} = 16350\) مبلغ پرداختی توسط مشتری
مثال
فروشنده ای قیمت کالایی را پس از محاسبه ی8% مالیات بر ارزش افزوده مبلغ ۷۵۶۰ تومان اعلام کرد. قیمت اصلی این کالا قبل از مالیات چه قدر بوده است؟
۷۵۶۰ تومان همان ۱۰۸ درصد قیمت اصلی می باشد، بنابراین
\(7560 + \frac{{108}}{{100}} = 7560 \times \frac{{100}}{{108}} = 7000\) = قیمت کالا بدون مالیات
کاربرد درصد در آمار و احتمال
فصل 6 : تناسب و درصد
کاربرد درصد در آمار و احتمال
یک دایره کامل زاویه ۳۶۰ درجه را نشان می دهد.
مثال
دایره ی مقابل به چند بخش با رنگهای مختلف تقسیم شده و اندازه ی زاویه ی مربوط به هر بخش نوشته شده است. درصد مساحت هر بخش را به کل دایره بنویسید.
\(\begin{array}{l}\frac{{90^\circ }}{{360^\circ }} = \frac{1}{4} = \frac{{25}}{{100}} \to 90^\circ \to 25\% \\\\\frac{{54^\circ }}{{360^\circ }} = \frac{{54^\circ \div 18}}{{360^\circ \div 18}} = \frac{3}{{20}} = \frac{{15}}{{100}} \to 54^\circ \to 15\% \\\\\frac{{72^\circ }}{{360^\circ }} = \frac{{72^\circ \div 18}}{{360^\circ \div 18}} = \frac{4}{{20}} = \frac{{20}}{{100}} \to 72^\circ \to 20\% \end{array}\)
مثال
%۳۰ دانش آموزان کلاسی در رشته ی بسکتبال ۵۰% در رشته ی فوتبال و ٪۲۰ در رشته ی والیبال شرکت دارند. نمودار دایره ای مربوط به این داده ها را رسم کنید.
روش محاسبه ی دیگر:
اکنون دایره ای را رسم میکنیم و قسمتهای مختلف را با استفاده از نقاله معین می کنیم.
مثال
در نمودار دایره ای ٪۶۰ یعنی چند درجه؟
\(\frac{{60}}{{100}} \times 360^\circ = 216^\circ \)
در داخل کیسه ای ۱۰ کارت وجود دارد که روی هر یک از آنها اعداد از ۱ تا ۱۰ نوشته شده است. اگر بدون نگاه کردن به داخل کیسه یک کارت را بیرون بیاوریم:
الف احتمال این که عدد روی کارت بزرگ تر از ۶ باشد، چه قدر است؟
اعداد بزرگ تر از ۶ یعنی ۷، ۸، ۹ یا ۱۰.
\(\begin{array}{l}\frac{4}{{10}} = \frac{{40}}{{100}} = 40\% \\\\\frac{4}{{10}} = \frac{{144^\circ }}{{360^\circ }}\end{array}\)
ب احتمال این که عدد روی کارت کم تر از ۳ باشد، چه قدر است؟
یعنی عدد ۱ یا ۲ روی کارت باشد، پس:
\(\begin{array}{l}\frac{2}{{10}} = \frac{{20}}{{100}} = 20\% \\\\\frac{2}{{10}} = \frac{{72^\circ }}{{360^\circ }}\end{array}\)
ج نمودار دایره ای مربوط به موارد بالا را رسم کنید.
د باقی ماندهی نمودار دایره ای مربوط به کدام اعداد روی کارت ها است؟
باقی ماندهی نمودار مربوط به عددهای بین ۲ و ۷ یعنی (۳، ۴، ۵ یا ۶) می باشد.
نمودار دایره ای
فرض کنید که در یک نظرسنجی از دوستان خود میزان علاقه مندی آنها به انواع برندهای معروف اتومبیل را پرسیده اید و اطلاعات به دست آمده را در جدول زیر وارد کرده اید.
همان طور که ملاحظه میکنید، در مجموع از ۲۰ نفر نظرسنجی شده است. حال اگر نسبت هر یک از عددها به ۲۰ را حساب کنیم و سپس در عدد ۱۰۰ ضرب کنیم درصد علاقه مندی به هر برند مشخص می شود.
\(\frac{6}{{100}} \times 100 = 30\,\,\,\,,\,\,\,\,\frac{5}{{20}} \times 100 = 25\% \,\,\,\,,\,\,\,\,\frac{2}{{20}} \times 100 = 10\% \,\,\,\,\,,\,\,\,\,\,\,\,\frac{3}{{20}} \times 100 = 15\% \,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\frac{4}{{20}} \times 100 = 20\% \)
حالا مانند شکل مقابل یک دایره را به ۱۰۰ قسمت مساوی تقسیم می کنیم.
هر قسمت نشان دهنده ی یک درصد است سپس درصد مربوط به هر کدام از اتومبیل ها را روی شکل مشخص می کنیم همان طور که ملاحظه میکنید تقسیم یک دایره به ۱۰۰ قسمت مساوی کمی سخت و دشوار است و شاید قسمتها به طور دقیق تقسیم نشوند لذا بهتر است روش دیگری را برای رسم چنین نموداری یاد بگیریم در این روش کافی است که زاویه ی مربوط به هر یک از درصدهای بالا را با استفاده از جدول تناسب زیر مشخص کنیم. دقت داشته باشید که یک دایره ی کامل یک زاویه ی ۳۶۰ درجه را نشان می دهد از طرفی دایره ی بالا را به ۱۰۰ قسمت مساوی تقسیم کردیم. پس حالا با استفاده از این جدول تناسب زاویه ها را مشخص می کنیم:
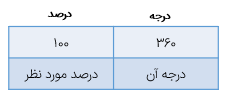
اکنون یک دایره رسم کرده و مرکز آن را مشخص میکنیم سپس با کمک یک نقاله و قرار دادن مرکز نقاله روی مرکز دایره زاویه ی مربوط به هر قسمت را مشخص میکنیم تا شکل موردنظر به دست آید.
پرتاب سکه
وقتی یک سکه را میاندازیم یا روی سکه بالا قرار میگیرد و یا پشت آن اما انتظار داریم تقریبا در نصف (یعنی ۵۰ درصد) پرتاب ها رو و در نصف ۵۰ (درصد دیگر پرتاب ها هم پشت سکه بیابید که در اصطلاح می گوییم احتمال رو آمدن و پشت آمدن سکه ۵۰ - ۵۰ است.
مثال
یک سکه را ۵۰۰ مرتبه انداخته ایم نتیجه این آزمایش در جدول زیر دیده می شود. در چند آزمایش سکه رو آمده است؟
برای پیدا کردن جواب کافی است که درصد رو آمدن یعنی (۴۷/۴) را در عدد ۵۰۰ ضرب کنیم.
پرتاب تاس
وقتی که یک تاس را می اندازیم حتما یکی از عددهای ۱ ۲ ۳ ۴ ۵ و یا ۶ در روی تاس ظاهر می شوند. پس در پرتاب ۳۰ مرتبه یک تاس انتظار داریم هر کدام از وجه ها (عددهای ۱ تا ۶) را تقریبا ۵ مرتبه مشاهده کنیم. در این آزمایش احتمال وقوع و یا ظاهر شدن هر یک از عددها از نصف یعنی ۵۰ درصد کم تر است.
به طور مثال احتمال ظاهر شدن عدد ۵ از نصف کم تر است اما احتمال ظاهر شدن عدد فرد، ۵۰ - ۵۰ می باشد. به جدول زیر دقت کنید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تقریب به روش گردکردن
فصل 7 : تقریب
تقریب به روش گرد کردن
برای این که در استفاده از عددهای تقریبی خطای کم تری داشته باشیم از روش گرد کردن استفاده می کنیم. در این روش با توجه به تقریب مورد نظر عددی را به صورت تقریبی انتخاب میکنیم که به مقدار واقعی نزدیک باشد. برای مثال مقدار تقریبی عدد ۷۸۳ با تقریب کمتر از ۱۰۰ و روش گرد کردن برابر ۸۰۰ می شود، چون عدد ۸۰۰ به عدد ۷۸۳ نزدیک تر از عدد 70۰می باشد.
مثال
با تقریب کمتر از ۰/۱ به روش گرد کردن عدد ۴۳/۱۹ به عدد ۴۳/۲ نزدیک تر است تا عدد ۴۳/۱.
بنابراین گردشده ی عدد ۴۳/۱۹ با تقریب کم تر از ۰/۱ به روش گرد کردن، برابر است با ۴۳/۲.
در روش گرد کردن ابتدا به رقم سمت راست تقریب توجه میکنیم اگر این رقم ۵ یا بزرگ تر از ۵ باشد (یعنی ۵، ،۶ ،۷ ،۸ یا ۹ باشد) یک واحد به رقم تقریب اضافه کنیم و سپس رقمهای سمت راست تقریب را با صفر جایگزین میکنیم و اگر رقم سمت راست تقریب کوچک تر از ۵ (یعنی ۴ ۳ ۲ ۱ یا صفر) باشد بدون این که به رقم تقریب چیزی اضافه کنیم رقم های سمت راست تقریب را با صفر جایگزین می کنیم.
مثال
عدد ۴۵۹۳ را با تقریب کم تر از ۱۰۰۰ گرد کنید.
مثال
مقدار تقریبی عددهای داده شده را با تقریب کمتر از ۱۰ به دو روش بنویسید.
1 اگر رقم سمت راست تقریب کمتر از ۵ ،باشد پاسخ تقریبی به روش قطع کردن و گرد کردن یکسان می شود.
\(\begin{array}{l}7523/4 \simeq 7500\\\\7523/4 \simeq 7500\end{array}\)
2 برای محاسبه مقدار تقریبی کسرها به روش گرد کردن باید خارج قسمت تقسیم را تا یک رقم بیشتر از تقریب داده شده محاسبه کنیم؛ یعنی اگر بخواهیم مقدار تقریبی کسری را به روش گردکردن با تقریب کم تر از ۰/۰۱ محاسبه کنیم باید خارج قسمت را تا سه رقم اعشار یک رقم بیشتر از رقم های اعشاری (۰/۰۱) محاسبه کنیم و سپس عدد اعشاری به دست آمده را با تقریب داده شده گرد کنیم
مثال
مقدار تقریبی عدد\(\frac{{23}}{7}\) را با تقریب کم تر از ۰/۰۰۱ به روش گردکردن محاسبه کنید.
باید حاصل تقسیم ۲۳ بر ۷ را تا چهار رقم اعشار یعنی یک رقم بیشتر از رقم های اعشار ۰/۰۰۱ حساب کنیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
تقریب به روش قطع کردن
فصل 7 : تقریب
تقریب
در محاسبه های تقریبی برای نشان دادن مقدار تقریبی ،عددها به جای علامت مساوی از علامت \( \simeq \)استفاده می کنیم که یعنی « تقریبا برابر است با ».
برای تقریب زدن عددها، دو روش داریم:
۱ روش قطع کردن
۲ روش گرد کردن
روش قطع کردن
در این روش رقم های سمت راست ،تقریب یعنی عددهایی را که ارزش مکانی آنها از تقریب داده شده، کم تر باشد با صفر جایگزین می کنیم.
مثال
با تقریب کمتر از ۱۰ در روش قطع کردن یعنی تمامی رقم هایی که ارزش مکانی آنها کم تر از دهگان است، به صفر تبدیل شوند.
تقریب کمتر از 10 به روش قطع کردن:
\(293 \simeq 290\)
با تقریب کم تر از ۱۰۰۰ در روش قطع کردن، یعنی تمامی رقم هایی که ارزش مکانی آن ها کم تر از یکان هزار است رقم های سمت راست (۳) به صفر تبدیل شوند.
تقریب کمتر از 1000 به روش قطع کردن:
\(43591 \simeq 43000\)
با تقریب دهگان یعنی با تقریب کمتر از ۱۰ با تقریب ،صدگان یعنی با تقریب کم تر از 100 .
مثال
عدد ۳۹/۷۴۱ را با تقریب کم تر از ۱ قطع کنید.
این عدد را در جدول ارزش مکانی قرار می دهیم وقتی می گوییم با تقریب کم تر از یک یعنی رقم هایی که ارزش مکانی آنها کم تر از یکان است باید به صفر تبدیل شوند.
وقتی میگوییم با تقریب کم تر از ۰/۰۱ یعنی رقم هایی که در مرتبه ی هزارم و ده هزارم و ... قرار دارند، به صفر تبدیل شوند.
مثال
مقدار عدد\(\pi \)تا هشت رقم اعشار برابر است با:
\(\pi = 3/14159265\)
مقدار عدد 7 با تقریب کمتر از ۰/۰۱ تا دو رقم اعشار:
\(\pi = 3/14\)
مقدار عدد با تقریب کمتر از ۰/۰۰۰۱ تا چهار رقم اعشار:
\(\pi = 3/1415\)
مقدار عدد با تقریب کمتر از ۰/۱ تا یک رقم اعشار:
\(\pi = 3/1\)
با تقسیم صورت هر کسر بر مخرج آن میتوان آن کسر را به صورت عدد اعشار نوشت.
وقتی می گوییم تقسیم را تا یک رقم اعشار انجام دهید یعنی خارج قسمت را با تقریب کم تر از ۰/۱ به دست آورید و یا وقتی میگوییم تقسیم را تا دو رقم اعشار انجام دهید یعنی خارج قسمت را با تقریب کم تر از ۰/۰۱ حساب کنید.
در تقریب رقم دهگان اختلاف هر عدد با مقدار تقریبی آن کوچک تر از ۱۰ است.
مثال
مقدار تقریبی کسر\(\frac{{24}}{7}\) را تا سه رقم اعشار حساب کنید.
برای محاسبه ی مقدار تقریبی کسرها به روش قطع کردن فقط کافی است که خارج قسمت تقسیم را به اندازه ی رقم های اعشاری عدد تقریب محاسبه کنیم. برای مثال اگر بخواهیم مقدار تقریبی کسر\(\frac{{19}}{{11}}\) را با تقریب کم تر از ۰/۰۱ به روش قطع کردن حساب کنیم باید خارج قسمت تقسیم صورت بر مخرج کسر را تا ۲ رقم اعشار حساب کنیم.
مثال
مقدار تقریبی عدد\(\frac{{27}}{{13}}\) را با تقریب کم تر از ۰/۰۰۱ به روش قطع کردن حساب کنید.
چون ۰/۰۰۱ دارای سه رقم اعشار است و باید به روش قطع کردن تقریب ،بزنیم، بنابراین خارج قسمت تقسیم ۲۷ بر ۱۳ را تا سه رقم اعشار حساب می کنیم.
وقتی صحبت از سن افراد میشود مجبوری از عددهای تقریبی استفاده کنیم به طور مثال اگر سن رضا ۱۲ سال و ۵ ماه و ۱۷ روز باشد میگوییم سن رضا ۱۲ سال است و یا اگر وزن رضا ۵۳/۳۵۰ کیلوگرم باشد، می گوییم وزن رضا ۵۳ کیلوگرم است به چنین بیانی از مقدارهای تقریبی که همواره مقدار کم تر مورد نظر است، روش قطع کردن گفته می شود.
در روش قطع کردن رقم های سمت راست تقریب را که ارزش مکانی کم تری نسبت به رقم تقریب دارند، با صفر جایگزین میکنیم (یعنی به صفر تبدیل میکنیم) و خود رقم تقریب و همچنین رقم های مرتبه های بالاتر را بدون تغییر می نویسیم
به طور مثال وقتی میخواهیم مقدار تقریبی عدد ۵۶۷۳/۲۸۴ را با تقریب کمتر از ۱۰۰، به روش قطع کردن حساب کنیم با توجه به جدول ارزش مکانی این عدد که در قسمت زیر ملاحظه می کنید، تمامی رقم هایی که در مرتبه ی پایین تری از صدگان قرار دارند؛ یعنی رقم هایی که در مرتبه ی دهگان یکان دهم، صدم و هزارم قرار دارند را به صفر تبدیل نموده و بقیه رقم ها را بدون تغییر می نویسیم.
به این ترتیب ۳ مقدار تقریبی این عدد با تقریب کم تر از ۱۰۰ برابر ۵۶۰۰ خواهد شد.
در نمایش تقریبی عددها از علامت استفاده می کنیم و این علامت را تقریبا مساوی می خوانیم.
مثال
با تقریب کمتر از صدگان ۵۶۰۰ = ۵۶۷۳/۲۸۴
می خوانیم عدد ۵۶۷۳/۲۸۴ با تقریب کم تر از صدگان تقریبا مساوی با ۵۶۰۰ است.
در تقریب به روش قطع کردن همیشه اختلاف هر عدد با مقدار تقریبی آن کوچک تر از مقدار رقم تقریب است به طور مثال در تقریب رقم صدگان اختلاف هر عدد با مقدار تقریبی آن کوچک تر از صد است و یا در تقریب رقم دهگان اختلاف هر عدد با مقدار تقریبی آن کوچک تر از ده است به همین دلیل است که از این به بعد به جای عبارت (با تقریب کم تر از صدگان دهگان ،یکان دهم و ..) از عبارت (با تقریب کم تر از ۱۰۰، ۱۰، ۱، ۰/۱ و . ) استفاده می کنیم.
مثال
مقدار تقریبی هر یک از عددهای زیر را به روش قطع کردن و با تقریب خواسته شده بنویسید.
(با تقریب کم تر از ۱۰۰)\(1999/9\) الف
\(1999/9 \simeq 1900\)
(با تقریب کم تر از ۱۰)\(199/9\) ب
\(199/9 \simeq 1990\)
(با تقریب کمتر از ۱)\(35/742\) ج
\(35/742 \simeq 35\)
(با تقریب کمتر از10/1 )\(35/742\) د
\(35/742 \simeq 35/7\)
تقریب عددهای کسری
فصل 7 : تقریب
تقریب عددهای کسری
برای تقریب زدن عددهای کسری مانند\(\frac{{25}}{7}\) به روش قطع کردن ابتدا صورت کسر را بر مخرج آن تقسیم می کنیم، اگر تقسیم را تا یک رقم اعشار در خارج قسمت انجام دهیم یعنی حاصل را با تقریب کم تر از ۰/۱ به دست آورده ایم و اگر تقسیم را تا دو رقم اعشار در خارج قسمت انجام دهیم؛ یعنی حاصل را با تقریب کم تر از ۰/۰۱ به دست آورده ایم به همین ترتیب اگر تقسیم را تا سه رقم اعشار انجام دهیم؛ یعنی حاصل را با تقریب کم تر از ۰/۰۰۱ حساب کرده ایم.
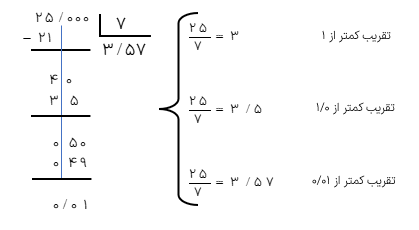
در کسرهایی مانند\(\frac{1}{2},\frac{1}{5}\) که مخرج آن ها فقط ۲ و یا فقط ۵ هستند، همه ی تقریب های آن ها مساوی اند زیرا مقدار دقیق تقسیم صورت این کسرها بر مخرج آنها تا یک رقم اعشار قابل محاسبه است.
مقدار تقریبی \(\frac{1}{2}\)با تمام تقریب های کم تر از ۰/۱ یا ۰/۰۱ یا ۰/۰۰۱ و ... برابر ۰/۵ است.
\(\frac{1}{2} = \frac{5}{{10}} = 0/5\)
مقدار تقریبی\(\frac{1}{5}\)با تمام تقریب های کم تر از ۰/۱ یا۰/۰۱ یا ۰/۰۰۱ و ... برابر ۰/۲ است.
\(\frac{1}{5} = \frac{2}{{10}} = 0/2\)
تقریب زدن به روش گرد کردن
در سال چهارم دبستان با تقریب زدن آشنا شدید و آموختید که برای تقریب زدن هر عددی با توجه به تقریب داده شده یک عدد رند قبل و یک عدد رند بعد از عدد مورد نظر می نویسیم و از بین آن ها عددی را که به عدد مورد نظر نزدیک تر است به عنوان مقدار تقریبی عدد در نظر میگیریم اما امسال می آموزیم که هرگاه بخواهیم مقدار تقریبی عددی را با (تقریب دهگان) و یا به عبارت دیگر با تقریب کمتر از ۱۰ به دست آوریم، باید به رقم يكان عدد دقت کنیم در صورتی که رقم یکان ۵ یا بیش تر از ۵ باشد ( یعنی ۵ ۶ ۷، ۸ و ۹)، به رقم دهگان یک واحد اضافه کرده و یکان را صفر میکنیم اما در صورتی که رقم یکان کم تر از ۵ باشد یعنی یکی از رقم های ۰، ۱، ۲، ۳ و ۴ در این صورت دهگان تغییر نمی کند و یکان هم صفر می.شود.
به مثال های زیر دقت کنید:
با تقریب دهگان ۵۷۰ = ۵۷۳ : روش سال ششم \( \Rightarrow \)۵۸۰ \( \Rightarrow \) ۵۷۳\( \Leftarrow \) ۵۷۰: روش سال چهارم
با تقریب دهگان ۱۴۳۰ = ۱۴۲۵ : روش سال ششم\( \Rightarrow \) ۱۴۳۰ \( \Rightarrow \) ۱۴۲۵ \( \Leftarrow \) ۱۴۲۰ : روش سال چهارم
هرگاه بخواهیم مقدار تقریبی عددی را با تقریب صدگان و یا به عبارت دیگر با تقریب کم تر از صد به دست آوریم باید به رقم دهگان عدد دقت کنیم در صورتی که رقم دهگان ۵ و یا بیش تر از ۵ (یعنی ۵ ۶ ۷، ۸و ۹) باشد به رقم صدگان یک واحد اضافه کرده و یکان و دهگان و قسمت اعشاری را صفر می کنیم. اما اگر رقم دهگان کم تر از ۵ ،باشد رقم صدگان تغییر نکرده و یکان و دهگان و قسمت اعشاری به صفر تبدیل می شوند.
به مثال های زیر دقت کنید:
با تقریب صدگان ۱۷۰۰ = ۱۷۴۳ : روش سال ششم۱۸۰۰\( \Rightarrow \)۱۷۴۳\( \Leftarrow \) ۱۷۰۰ : روش سال چهارم
با تقریب صدگان ۱۴۰۰ = ۱۳۵۲ : روش سال ششم۱۴۰۰\( \Rightarrow \) ۱۳۵۲ \( \Leftarrow \) ۱۳۰۰: روش سال چهارم
در تمامی مثال هایی که در قسمت قبل ملاحظه نمودید مقدار تقریبی عددها به روش گرد کردن به دست آمده اند. برای تقریب زدن عددها به روش گرد کردن به ترتیب زیر عمل می کنیم:
۱ رقمی را که باید گرد شود مشخص میکنیم به طور مثال در تقریب کمتر از ۱۰۰ باید زیر صدگان خط بکشیم.
2 به اولین رقم جلو سمت راست رقم مورد تقریب دقت میکنیم اگر این رقم ۵ یا بیش تر از ۵ (یعنی ۵، ۷،۶، ۸ و یا ۹) بود یک واحد به رقم مورد تقریب اضافه می کنیم در غیر این صورت رقم مورد تقریب تغییری نمی کند.
3 همه ی رقم های سمت راست رقم مورد تقریب را با صفر جایگزین میکنیم و یا به عبارت دیگر به صفر تبدیل می کنیم.
به مثال های زیر دقت کنید.
(با تقریب کم تر از ۱۰۰۰) با تقریب صدگان ۳۶۰۰۰ = ۳۵۸۴۵ (الف
رقم جلو هزارگان یعنی رقم صدگان برابر ۸ است پس یک واحد به رقم هزارگان اضافه نموده و تمامی رقم های
یکان دهگان و صدگان را به صفر تبدیل می کنیم.
(با تقریب کم تر از۱۰۰) با تقریب صدگان ۳۵۸۰۰ = ۳۵۸۴۵ (ب
رقم جلو صدگان یعنی دهگان برابر ۴ است پس رقم صدگان را بدون تغییر می نویسیم و تمامی رقم های یکان و دهگان را به صفر تبدیل می کنیم.
با تقریب دهگان ۳۵۸۵۰ = ۳۵۸۴۵ (ج
با تقریب یکان ۲۳۳۰ = ۲۳۲/۵ (د
مثال
مقدار تقریبی عدد ۱۷/۹۹۹ با تقریب کمتر از ۰/۰۱ مشخص کنید.
\(17/99 \simeq 18/000 = 18\)
۱ وقتی عددی را گرد میکنیم منظورمان گرد شده به نزدیک ترین عدد است. اگر رقم مربوط ۵ باشد، رقم مرتبه ی قبلی ) از سمت چپ را یک واحد افزایش می دهیم
2 در روش گرد کردن گاهی گرد کردن کاهشی (مانند مورد ب) و گاهی گرد کردن افزایشی (مانند مورد الف)می باشد.
3 در روش گرد کردن نیز اختلاف بین هر عدد و مقدار تقریبی آن (یعنی عدد بزرگ تر منهای عدد کوچک تر) همیشه از مقدار تقریب کم تر است.
محاسبه ی مقدار تقریبی کسرها به روش گردکردن
برای تقریب زدن اعداد کسری به روش گرد کردن ابتدا مقدار تقسیم صورت کسر بر مخرج آن را تا یک رقم بیش تر از تقریب داده شده به دست می آوریم، یعنی اگر تقریب کم تر از ۰/۱ باشد باید تقسیم را تا دو رقم اعشار حساب کنیم و سپس عدد به دست آمده را به روش گرد کردن تقریب می زنیم.
مثال
مقدار تقریبی کسر \(\frac{{27}}{7}\) به را با تقریب کمتر از ۰/۰۱ به روش گرد کردن حساب کنید.
ابتدا با توجه به این که روش گرد کردن و تقریب کمتر از ۰/۰۱ میباشد باید حاصل تقسیم را تا سه رقم اعشار در خارج قسمت حساب کنیم که برای این عمل میتوانیم از ماشین حساب هم کمک بگیریم سپس عدد به دست آمده (یعنی ۳/۸۵۷ ) را با تقریب داده شده گرد می کنیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
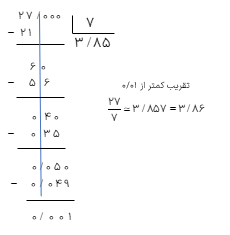
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تفاوت بین روش قطع کردن و گردکردن
فصل 7 : تقریب
تفاوت بین روش قطع کردن و گردکردن
در روش قطع کردن سرعت انجام محاسبات بیشتر است اما در روش گرد کردن جواب به دست آمده دقیق تر است. لذا استفاده از این روشها به اهمیت دقت پاسخ و سرعت انجام محاسبات بستگی دارد. در ضمن به یاد داشته باشید که اگر رقم جلوی تقریب کوچکتر از ۵ (یعنی ،۱۰، ۲، ۳ و یا ۴) باشد، مقدار تقریبی عدد با تقریب داده شده از هر دو روش یکسان است.
(قطع شده با تقریب کمتر از 10۰) ۵۳۰۰ = ۵۳۴۷
(گرد شده با تقریب کمتر از ۱۰۰) ۵۳۰۰ = ۵۳۴۷
(قطع شده با تقریب کمتر از ۱۰۰) ۲۷۰۰ = ۲۷۶۴
(گرد شده با تقریب کمتر از ۱0۰) ۲۸۰۰ = ۳۷۶۴
اگر رقم سمت راست تقریب کمتر از ۵ ،باشد جواب به دست آمده در هر دو روش قطع کردن و گرد کردن یکی می شود.
نمایش تقریبی عددها روی محور
اگر بخواهیم عددی مانند\(\frac{5}{7}\) را روی محور نمایش دهیم به دلیل این که تقسیم یک واحد به ۷ قسمت مساوی کمی سخت است بهتر است که از نمایش تقریبی این عدد روی محور استفاده کنیم اگر حاصل تقسیم صورت کسر بر مخرج آن را تا یک رقم اعشار در خارج قسمت حساب کنیم مقدار تقریبی این عدد با تقریب ۰/۱ به دست می آید. حال اگر بخواهیم که موقعیت دقیق تری از این عدد روی محور نمایش دهیم کافی است که تقسیم را تا دو رقم اعشار ادامه دهیم تا مقدار تقریبی عدد با تقریب ۰/۰۱ به دست آید.
به این ترتیب موقعیت جدید از موقعیت قبلی دقیق تر میباشد و به همین ترتیب با پیشروی در تقسیم باز هم موقعیت های دقیق تری نسبت به قبل به دست می آید.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
عدد پی
فصل 7 : تقریب
عدد پی
به مقدار تقریبی عددهای عدد \(\pi = \frac{{22}}{7}\) (بخوانید عدد پی) تا ۵ رقم اعشار دقت کنید مقدار تقریبی این دو عدد با تقریب کمتر از ۰/۱ و ۰/۰۱ دقیقا با هم برابر میباشد. لذا میتوانیم گاهی اوقات به جای عدد\(\pi \) از کسر \( \frac{{22}}{7}\)هم استفاده کنیم.
\(\frac{{22}}{7} = 3/14285\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\pi = 3/14159\)
مثال
۴ شعاع دایره ای ۷ سانتی متر است. محیط و مساحت این دایره را حساب کنید. ( ۳/۱۴ = \(\pi \))
روش اول
۴۳/۹۶ = ۳/۱۴×۷×۲ =\(\pi \)x قطر = محیط دایره محیط دایره
۱۵۳/۸۶ = ۳/۱۴× ۷ × ۷ =\(\pi \)x شعاع x شعاع = مساحت دایره
روش دوم
\(2 \times 7 \times \frac{{22}}{7} = 44\) =محیط دایره
\(7 \times 7 \times \frac{{22}}{7} = 154\) =مساحت دایره
همان طور که ملاحظه می کنید زمانی که به جای مقدار تقریبی عدد\(\pi \) از کسر\(\frac{{22}}{7}\)استفاده کردیم، مقادیر محیط و مساحت دایره با اختلاف بسیار ناچیزی نسبت به زمانی که مقدار تقریبی \(\pi \) را تقریبا مساوی ۳/۱۴ در نظر گرفتیم به دست آمد.
دقت اندازه گیری
فصل 7 : تقریب
دقت اندازه گیری
به خط کش مقابل دقت کنید.
کوچک ترین قسمتی که روی این خط کش مشخص شده ۰/۵ سانتی متر یا ۵ میلی متر است، بنابراین دقت اندازه گیری این خط کش ۵/ سانتی متر است؛ یعنی این خط کش اندازههای کم تر از ۰/۵ سانتی متر یا ۵ میلی متر را برای ما مشخص نمیکند اندازه ی مدادی که روی شکل دیده میشود بین ۳/۵ و ۴ سانتی متر است. چون خط کش نمی تواند بین این دو عدد را برای ما مشخص کند و اندازه ی مداد به ۳/۵ سانتی متر نزدیک تر است، ما اندازه ی مداد را به طور تقریبی ۳/۵ سانتی متر در نظر میگیریم اختلاف اندازه ی واقعی مداد و عدد ۳/۵ از 0/5 سانتی متر کم تر است بنابراین میگوییم این خط کش اندازه اشیا را با تقریب کم تر از ۰/۵ سانتی متر مشخص میکند در خط کشهای معمولی کوچک ترین قسمتی که روی آنها مشخص شده، ۱ میلی متر است؛ یعنی دقت اندازه گیری این خط کش ها ۱ میلی متر است؛ یعنی این خط کش ها اندازه ی اشیا را با تقریب کم تر از ۱ میلی متر مشخص می کنند.
برای هر نوع اندازه گیری با توجه به موضوع و اهمیت آن از ابزار مناسب استفاده می کنیم تا تقریب مورد نظر حاصل شود.
برای اندازه گیری وزن یک انسان به ترازویی با دقت تا ۱ کیلوگرم نیاز داریم.
برای اندازه گیری دمای بدن انسان به دماسنجی با دقت تا ۱ درجه نیاز داریم.
برای اندازه گیری وزن فلزات و سنگ های گرانبها به ترازویی با دقت تا ۰/۱ گرم نیاز داریم.
در محاسبه های تقریبی، با توجه به شرایط ابتدا عددها را تقریب میزنیم و سپس محاسبه را انجام می دهیم و یا در بعضی موارد ابتدا محاسبه را انجام می دهیم و سپس حاصل را تقریب میزنیم.
مثال
قیمت فروش نوعی ،تخته متر مربعی ۸۰۰۰ تومان است. قیمت تخته ای به ابعاد ۳/۴۴ و ۲/۸۳ متر چند تومان است؟
روش ۱ ابتدا ابعاد تخته را با تقریب کم تر از ۰/۱ گرد میکنیم و مساحت را حساب می کنیم.
\(2/8 \times 3/4 = 9/52\)متر مربع
روش ۲ ابتدا مساحت تخته را حساب می کنیم و سپس عدد حاصل را با تقریب کم تر از ۰/۰۱ گرد می کنیم.
متر مربع\(2/83 \times 3/44 = 9/7352\)
\(9/7352 \simeq 9/74\)
همان طور که ملاحظه می کنید در روش دوم مساحت به دست آمده به مساحت واقعی تخته نزدیک تر است؛ بنابراین در این مسئله بهتر است که ابتدا مساحت را به دست آورده و سپس عدد حاصل را تقریب بزنیم.
قیمت تخته تومان ۷۷۹۲۰ = ۸۰۰۰× ۹/۷۴
هر یک از عددهای مخلوط زیر را با تقریب کم تر از ۱ گرد کنید.
الف \(17\frac{1}{5}\)
چون \(\frac{1}{5}\)از نصف تقریب (نصف عدد ۱ یعنی\(\frac{1}{2}\) ) کم تر است، بنابراین:
\(17\frac{1}{5} \simeq 17 + 0 = 17\)
ب \(3\frac{4}{5}\)
چون\(\frac{4}{5}\) عدد از نصف بیشتر است، بنابراین:
\(3\frac{4}{5} \simeq 3 + 1 = 4\)
ج \(29\frac{7}{8}\)
چون \(\frac{7}{8}\)از نصف بیشتر است، بنابراین:
\(29\frac{7}{8} \simeq 29 + 1 = 30\)
ترتیب انجام عملیات
در محاسبات ریاضی، ترتیب انجام عملیات تقدم (محاسبات) به شکل زیر است:
۱ ابتدا حاصل پرانتزها را حساب میکنیم و اگر چندین پرانتز داخل هم باشند از داخلی ترین پرانتز محاسبه را شروع می کنیم.
۲ بعد از محاسبه ی پرانتزها، عملهای ضرب و تقسیم را انجام می دهیم. از چپ به راست
3 بعد از محاسبه های ضرب و تقسیم از چپ به راست محاسبه های جمع و تفریق را انجام می دهیم.
مثال
حاصل عبارت های زیر را به دست آورید.
الف \(2 + 3 \times 5\)
\(2 + 3 \times 5 = 2 + 15 = 17\)
ب\(2 + 4 \times (8 - 3)\)
\(2 + 4 \times (8 - 3) = 2 + 4 \times = 2 + 20 = 22\)
ج\(8 - 12 \div (1/2 + (3/6 \div 2)) \)
\(8 - 12 \div (1/2 + (3/6 \div 2)) = 8 - 12 \div (1/2 + 1/8) = 8 - 12 \div 3 = 8 - 4 = 4\)
اندازه گیری
هر وسیله ی اندازه گیری تا حدی میتواند عدد یا مقدار دقیق چیزی را که اندازه میگیریم، نشان دهد. برای مثال، اکثر خط کش هایی که در اختیار دانش آموزان قرار دارد تا واحد میلی متر را نشان می دهد. این خط کش ها طول های کم تر از یک میلی متر را مشخص نمیکنند بنابراین میگوییم خط کش طول اجسام و یا خط ها را با تقریب کم تر از ۱ میلی متر نشان میدهد از طرفی چون هر میلی متر مساوی ۰/۱ سانتی متر است. می توانیم بگوییم که دقت خط کش با تقریب کم تر از ۰/۱ سانتی متر است.
برای هر نوع اندازه گیری با توجه به موضوع و اهمیت آن از وسیله ی اندازه گیری مناسبی استفاده می کنیم تا تقریب مورد نظر ما حاصل شود.
به طور مثال برای اندازه گیری وزن اشخاص از واحد کیلوگرم استفاده میکنیم به عبارت دیگر، ترازوها معمولا وزن اشخاص را با تقریب کمتر از ۱ کیلوگرم نشان میدهد البته ترازوهای دیجیتال دقت بالاتری دارند یا برای اندازه گیری وزن یک قطعه طلا از ترازویی استفاده می کنند که دقت آن ۰/۰۱ گرم میباشد. به عبارت دیگر، این گونه ترازوها وزن اجسام را با تقریب کم تر از ۰/۰۱ گرم نشان می دهند.
کاربرد مقدار تقریبی
گاهی اوقات بهتر است اعداد را به صورت تقریبی بیان کنیم تا انجام محاسبه روی آنها ساده تر شود. در این صورت مقدار محاسبه شده با مقدار واقعی برابر نیست ولی به آن نزدیک است. به مثال زیر دقت کنید:
۵۲۷ × ۶۷۹ = ۳۵۷۸۳۳
همان طور که ملاحظه کنید حاصل ضرب دو عدد ۵۲۷ و ۶۷۹ دقیقا مساوی ۳۵۷۸۳۳ شد. حال اگر مقدار دقیق حاصل ضرب مورد نیاز نباشد و فقط بخواهیم مقدار تقریبی آن را به دست آوریم کافی است که مقدارهای تقریبی این دو عدد را در یک دیگر ضرب کنیم:
با تقریب صدگان ۵۰۰ = ۵۲۷
با تقریب صدگان ۷۰۰ = ۶۷۹
\( \Rightarrow 527 \times 679 = 500 \times 700 = 350000\)
بنابراین زمانی که هر یک از عددها را با تقریب صدگان گرد ،کنیم مقدار تقریبی حاصل ضرب برابر ۳۵۰۰۰۰ خواهد شد که این مقدار نزدیک به جواب واقعی همان ۳۵۷۸۳۳ میباشد. حال اگر عددها را تقریب دهگان گرد می کردیم جواب تقریبی به دست آمده نسبت به تقریب صدگان دقیق تر خواهد شد.
با تقریب دهگان ۵۳۰ = ۵۲۷
679 با تقریب دهگان ۶۸۰ =
\( \Rightarrow 527 \times 679 = 530 \times 680 = 360400\)
همان طور که ملاحظه می کنید مقدار تقریبی حاصل ضرب دو عدد در این حالت اختلاف کم تری نسبت به حالت قبل دارد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
محاسبه ی تقریبی
فصل 7 : تقریب
محاسبه ی تقریبی
برای انجام محاسبات تقریبی میتوانیم از روش های زیر استفاده کنیم:
روش اول ابتدا عددها را گرد کنیم سپس محاسبه را انجام دهیم.
روش دوم ابتدا حاصل را به دست آورده سر ، سپس پاسخ را گرد کنیم.
مثال
الف حاصل عبارت ۵۵ - ۲۹ + ۴۴ را به دست آورید. سپس جواب به دست آمده را با تقریب کم تر از ۱۰ گرد کنید.
\(44 + 29 - 55 = 73 - 55 = 18 = 20\)(با تقریب کمتر از ۱۰)
ب ابتدا مقدار تقریبی هر یک از عددهای بالا را با تقریب کم تر از ۱۰ به دست آورده سپس حاصل عبارت را به دست آورید.
مقدار تقریبی عددها با تقریب کم تر ۱۰
\(\begin{array}{l}44 \simeq 40\,\,,\,\,29 \simeq 30\,\,\,,\,\,\,\,55 \simeq 60\\44 + 29 - 55 \simeq 40 + 30 - 60 = 70 - 60 = 10\end{array}\)
همان طور که ملاحظه میکنید مقدار دقیق این عبارت برابر ۱۸ شد و وقتی که مقدار تقریبی جواب را با تقریب کم تر از ۱۰ گرد میکنیم حاصل ۲۰ می.شود پس اختلاف مقدار تقریبی با مقدار دقیق ۲ واحد است. اما اگر ابتدا عددها را گرد کنیم و سپس حاصل را به دست آوریم جواب برابر ۱۰ میشود که اختلاف این عدد با مقدار دقیق برابر ۸ = ۱۰ - ۱۸ واحد میباشد پس استفاده از روش اول بهتر است.
اگر ابتدا حاصل عبارت ۵۵ - ۲۹ + ۴۴ را به دست آوریم و سپس جواب به دست آمده را با تقریب کم تر از ۱۰ قطع کنیم خواهیم داشت:
قطع شده با تقریب کمتر از ۱۰
\(44 + 29 - 55 = 73 - 55 = 18 \simeq 10\)
حال اگر مقدار تقریبی هر یک از عددها را با روش قطع کردن و با تقریب کمتر از ۱۰ تقریب بزنیم و سپس محاسبه ی عبارت را انجام دهیم، خواهیم داشت:
مقدار تقریبی عددها با تقریب کمتر از10
\(\begin{array}{l}44 \simeq 40\,\,\,,\,\,\,\,29 \simeq 20\,\,\,,\,\,\,\,\,55 \simeq 50\\44 + 29 - 55 = 40 + 20 - 50 = 10\end{array}\)
به این ترتیب حاصل عبارت از هر دو روش یکسان خواهد شد لذا توصیه میکنیم که در محاسبات تقریبی برای این که جواب به دست آمده به مقدار واقعی نزدیک تر باشد از روش گرد کردن استفاده کنید.
وقتی هم باید عملیات انجام گیرد و هم تقریب بزنیم برای آن که پاسخ به مقدار واقعی نزدیک تر باشد، باید ابتدا عملیات را انجام دهیم و بعد از آن تقریب بزنیم.
الف حاصل ضرب ۱۱/۹ و ۲۵/۲ را به دست آورید.
\(25/2 \times 11/9 = 299/88\)
ب حاصل ضرب ۱۱/۹ × ۲۵/۲ را با قطع اعشار و با تقریب کم تر از ۱ به دست آورید.
۲۵/۲ = ۲۵/۲×۱۱/۹ = ۲۵×۱۱ = ۲۷۵
ج حاصل ضرب ۱۱/۹ × ۲۵/۲ را ابتدا با قطع اعشار و تقریب کم تر از ۱۰ به دست آورید.
۲۵/۲ = ۲۵/۲×۱۱/۹ = ۲۰×۱۰ = ۲۰۰
د در کدام ،حالت اختلاف با پاسخ واقعی کم ترین مقدار است؟
همان طور که دیده میشود، در حالت (ب)، یعنی حالتی که رقم مورد تقریب کوچک تر است مقدار تقریبی به مقدار واقعی نزدیک است. اختلاف جواب ها بسیار زیاد میباشد و جواب در حالت ،(ب) به مقدار واقعی نزدیک تر است. لذا باید در محاسبات خود از تقریب مناسب استفاده کنیم همچنین اگر به جای روش قطع کردن از روش گرد کردن استفاده می کردیم جواب ها با اختلاف بسیار کم تری نسبت به روش قطع کردن به دست می آمدند.
\(25/2 \simeq 25\,\,,\,\,11/9 \simeq 12\, \to 25/2 \times 11/9 = 25 \times 12 = 300\)
\(25/2 \simeq 30\,\,,\,\,\,\,11/9 \simeq 10 \to 25/2 \times 11/9 \simeq 30\,\, \times 10 \simeq 300\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم
جزوه جامع علوم تجربی ششم
جزوه جامع مطالعات اجتماعی ششم
جزوه جامع فارسی ششم
جزوه جامع نگارش ششم
جزوه جامع آموزش قرآن ششم
جزوه جامع کار و فناوری ششم
جزوه جامع تفکر و پژوهش ششم
جزوه جامع هدیه های آسمانی ششم
ترتیب انجام عملیات
فصل 7 : تقریب
ترتیب انجام عملیات
در انجام عملیات محاسباتی باید به ترتیب زیر عمل کنیم:
۱) محاسبه ی عبارت داخل پرانتزها
۲) انجام ضرب یا تقسیم از چپ به راست عبارت هر کدام که زودتر دیده شد.
۳) انجام جمع یا تفریق از چپ به راست عبارت هر کدام که زودتر دیده شد.
بنابراین اگر ترتیب عملیات با پرانتز مشخص نشده باشد، ابتدا باید ضربها و تقسیم ها و سپس جمع ها و تفریق ها را از چپ به راست عبارت انجام دهیم.
مثال
به عبارات زیر دقت کنید.
الف \(5/2 + 1/3 \times 7/1 = 5/2 + (1/3 \times 7/1) = 5/2 + 9/23 = 14/43\)
ب \(20 - 20 \div 4 \times 2 = 20 - (20 \div 4) \times 2 = 20 - (5 \times 2) = 20 - 10 = 10\)
دقت داشته باشید که چون در این عبارت پرانتزی وجود ندارد پس ابتدا به سراغ محاسبه ی تقسیم و سپس ضرب می رویم چون تقسیم زودتر از ضرب دیده میشود و در آخر تفریق را انجام می دهیم.
عبارت زیر را حل کنید
\((5\frac{1}{4} - 3\frac{3}{{10}}) \div (7/1 + 0/7)\)
محاسبه پرانتز اول:
\(5\frac{1}{4} - 3\frac{3}{{10}} = 2\frac{{1 \times 5}}{{4 \times 5}} - \frac{{3 \times 2}}{{10 \times 2}} = 2\frac{5}{{20}} - \frac{6}{{20}} = \frac{{45}}{{20}} - \frac{6}{{20}} = \frac{{39}}{{20}}\)
محاسبه پرانتز دوم:
\(7/1 + 0/7 = 7/8 = \frac{{78}}{{10}}\)
محاسبه کل عبارت:
\(\frac{{39}}{{20}} \div \frac{{78}}{{10}} = \frac{{39}}{{20}} \times \frac{{10}}{{78}} = \frac{1}{4}\)