آیا درسنامه فیزیک (2) رشته ریاضی فصل 1 الکتریسیتۀ ساکن، مطابق با آخرین تغییرات کتب درسی است ؟

بله، درسنامه فیزیک (2) رشته ریاضی فصل 1 مطابق با آخرین تغییرات کتب درسی 1402 - 1401 تدوین شده است.

آیا نکات درس به صورت کامل بیان شده اند ؟

بله، تمام نکات به صورت کاملا شیوا و با هدف یادگیری و تسلط به مبحث بیان شده اند.

درسنامه کامل فیزیک (2) رشته ریاضی فصل 1 الکتریسیتۀ ساکن

تعداد بازدید : 3.76M

خلاصه نکات فیزیک (2) رشته ریاضی فصل 1 الکتریسیتۀ ساکن - درسنامه شب امتحان فیزیک (2) رشته ریاضی فصل 1 الکتریسیتۀ ساکن - جزوه شب امتحان فیزیک (2) رشته ریاضی نوبت اول فصل 1 الکتریسیتۀ ساکن

قانون کولن

بزرگی نيروی الکتريکی ربايشی يا رانشی بين دو ذره با بارهای \({q_1}\) و \({q_2}\) که در فاصله r از يکديگر قرار دارند، با حاصل ضرب اندازه (بزرگی) بار دو ذره نسبت مستقيم و با مجذور فاصله دو ذره از هم، نسبت وارون دارد.

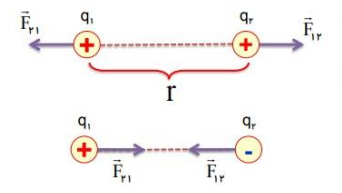
\({F_{12}}\) به معنای نیرویی است که ذره اول به ذره دوم وارد می کند.

\({F_{21}}\) به معنای نیرویی است که ذره دوم به ذره اول وارد می کند.

\(F = K\frac{{\left| {{q_1}} \right| \times \left| {{q_2}} \right|}}{{{r^2}}}\)

در این فرمول

(K) ثابت کولن (\(\frac{{N{m^2}}}{{{C^2}}}\) )

\(\begin{array}{l}K = \frac{1}{{4\pi {\varepsilon _0}}} \approx 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\\{\varepsilon _0} = 8/85 \times {10^{ - 12}}\frac{{{C^2}}}{{N{m^2}}}\end{array}\)

مثال

دو ذره با بارهای الکتریکی \( - 2\mu c\) و \(5\mu c\) در فاصله \(3cm\) از یکدیگر ثابت شده اند، اندازه نیرویی که دو ذره به یکدیگر وارد می کنند و نوع آن را مشخص کنید. (\(K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\) )

\(\begin{array}{l}{q_1} = - 2\mu c = 2 \times {10^{ - 6}}C\\{q_2} = 5\mu c = 5 \times {10^{ - 6}}C\\r = 3cm = 3 \times {10^{ - 2}}m\\K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\\F = ?\\F = K\frac{{\left| {{q_1}} \right|\left| {{q_2}} \right|}}{{{r^2}}} \to F = 9 \times {10^9}\frac{{\left| {2 \times {{10}^{ - 6}}} \right|\left| {5 \times {{10}^{ - 6}}} \right|}}{{3 \times {{10}^{ - 2}}}} = 100N \to F = 100N\end{array}\)

تکنیک 90

برای سادگی محاسبات می توان قانون کولن را به صورت \(F = 90\frac{{\left| {{q_1}} \right| \times \left| {{q_2}} \right|}}{{{r^2}}}\) نوشت؛ اما توجه کنيد در اين رابطه، اندازه ی بارها بر حسب \(\mu C\) و فاصله بر حسب cm جایگذاری شود.

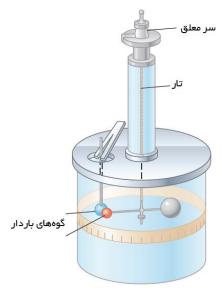
ترازوی پیچشی

در يک سر ميله نارسانای سبک افقی، يک گوی باردار مثبت کوچک و در سر ديگر آن، يک قرص جهت حفظ تعادل قرار دارد. ميله از وسط توسط يک رشته سيم کشسان و نازک آويخته شده است. يک گوی با بار منفی از حفرهای به داخل استوانه شيشه ای برده می شود. درجه هايی بر سطح استوانه حک شده است که ميزان چرخش ميله را نشان می دهد. نيروی موثر بين اين بارها از اندازه گيری زاويه چرخش تا رسيدن به حالت تعادل بدست می آيد .اين آزمايش اولين بار توسط دانشمندی فرانسوی به نام شارل آگوستين کولُن، جهت محاسبه ی بزرگی نيروی بين دو بار الکتريکی بنا شد و يکای بار الکتريکی به افتخار اين دانشمند فرانسوی، کولن ناميده می شود.

اصل برهم نهی نیرو های الکتریکی

نيروی الکتريکی وارد بر هر ذره، برآيند نيروهايی است که هر يک از ذرات، در غياب ساير ذرات، بر آن ذره وارد می کنند. مثلا فرض کنيد n ذره ی باردار داشته باشيم، که در نزديکی بار نقطه ای \({q_0}\) قرار دارند. آنگاه نيروی خالص وارد بر بار نقطه \({q_0}\) به صورت جمع برداری بدست می آيد:

\({F_{T0}} = {F_{10}} + {F_{20}} + {F_{30}} + .... + {F_{n0}}\)

گام های اساسی حل مسائل بر هم نهی نيروی الکتريکی

اندازه نيروی الکتريکی ناشی از تک تک بارها را بر بار مورد نظر محاسبه می کنيم.
جهت نيروی الکتريکی هر بار را بر بارمورد نظر رسم می کنيم.
اندازه و جهت نيروی برآيند را محاسبه می کنيم.

مثال

دو ذره باردار \({q_1} = + 3\mu c\) و \({q_2} = - 3\mu c\) در فاصله \(6cm\) از یکدیگر واقع شده اند، بار الکتریکی \({q_3} = + 1\mu c\) را در وسط این دو ذره قرار می دهیم. نیروی برآیند وارد بر بار \({q_3}\) را محاسبه کنید. (\(K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\) )

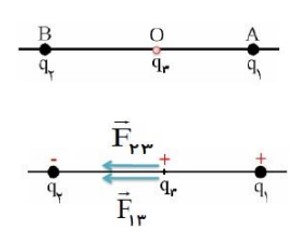
\(\begin{array}{l}{r_{13}} = 3cm = 3 \times {10^{ - 2}}m\\{r_{23}} = 3cm = 3 \times {10^{ - 2}}m\\{F_{13}} = K\frac{{\left| {{q_1}} \right|\left| {{q_3}} \right|}}{{{r_{13}}^2}} \to {F_{13}} = 9 \times {10^9}\frac{{3 \times {{10}^{ - 6}} \times 1 \times {{10}^{ - 6}}}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} \to {F_{13}} = - 30i\\{F_{23}} = K\frac{{\left| {{q_1}} \right|\left| {{q_3}} \right|}}{{{r_{13}}^2}} \to {F_{13}} = 9 \times {10^9}\frac{{\left| { - 3 \times {{10}^{ - 6}}} \right| \times 1 \times {{10}^{ - 6}}}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} \to {F_{23}} = - 30i\\{F_T} = {F_{13}} + {F_{23}}\\{F_T} = - 30i - 30i = - 60i\end{array}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران

پوشش تمام محتواهای درسی پایه ریاضی

آزمون آنلاین تمامی دروس پایه ریاضی
گام به گام تمامی دروس پایه ریاضی
ویدئو های آموزشی تمامی دروس پایه ریاضی
گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
فلش کارت های آماده دروس پایه ریاضی
گنجینه ای جامع از انشاء های آماده پایه ریاضی
آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی

کاملا رایگان

+500 هزار کاربر

همین حالا نصب کن

بار الکتریکی

کوچکترين باری که در طبيعت وجود دارد، بار الکتريکی الکترون و يا پروتون است که آن را با نماد (e) نمايش می دهند و مقدار آن برابر \(1/6 \times {10^{ - 19}}C\) است. مقدار بار الکتريکی جسم از رابطه \(q = \pm ne\) بدست می آيد، (علامت مثبت موقعی که جسم الکترون از دست بدهد، علامت منفی موقعی که جسم الکترون دريافت کند.)

1 از آنجا که تعداد الکترون های جا به جا شده همواره عدد درستی است، بار الکتريکی کميتی ناپيوسته است. يعني بار الکتريکی يک جسم نمي تواند \(1/25e\) و... باشد.

2 (e) را بار پایه (کوانتوم بار) می نامیم.

اصل کوانتيده بودن بار الکتريکی

بار الکتريکی همواره مضرب درستی از بار پايه يعنی الکترون (\( - e\)) و بار پروتون (\( + e\)) که در اتم های ماده وجود دارد، است. يک جسم نمی تواند بار الکتريکی \(5 \times {10^{ - 19}}C\) داشته باشد، ولی می تواند بار الکتريکی \(8 \times {10^{ - 19}}C\) داشته باشد، زیرا:

\(\begin{array}{l}q = 5 \times {10^{ - 19}}C \to n = \frac{q}{e} \to n = \frac{{5 \times {{10}^{ - 19}}}}{{1/6 \times {{10}^{ - 19}}}} = 3/125\\q = 8 \times {10^{ - 19}}C \to n = \frac{q}{e} \to n = \frac{{8 \times {{10}^{ - 19}}}}{{1/6 \times {{10}^{ - 19}}}} = 5\end{array}\)

روش های باردار کردن جسم

روش مالش

در اين روش، در اثر مالش دو ماده، تعدادی الکترون از يکی جدا شده و به ديگری انتقال می يابد. مثلا اگر يک ميله ی پلاستيکی را با پارچه پشمی مالش دهيم، ميله دارای بار منفي و پارچه ی پشمی به همان اندازه دارای بار مثبت می شود و هر گاه يک ميله ی شيشه ای را با پارچه ابريشمی مالش دهيم، ميله دارای بار مثبت و پارچه ی ابريشمی به همان اندازه دارای بار منفی می شود، اين روش معمولا برای باردار کردن اجسام نارسانا بکار می رود. در اين روش؛ دو جسم دارای بار الکتريکی همان اندازه ولی ناهمنام می شوند.

سری تريبو الکتريک (سری الکتريسته ی مالشی)

مثبت يا منفی شدن اجسام در اثر مالش به يکديگر، بر اساس جدول سری تريبو الکتريک مشخص می شود.

باردار کردن با روش تماس

هر گاه يک جسم رسانای باردار را با يک جسم رسانای خنثی تماس دهيم، مقداری بار از جسم باردار به جسم خنثی منتقل شده و بار هر دو همنام شده و يکديگر را می رانند. در اين روش هر دو جسم بايد رسانا باشند.

باردار کردن به روش القاء

در اين روش مطابق شکل، يک جسم باردار را به جسم رسانای بدون باری نزديک می کنند. در اثر القا، جسم دارای بار مثبت و منفی القايی می شود که بنا به قانون پايستگی بار الکتريکی، مقدار بار مثبت و منفی القا شده برابر است. ايجاد بار در رساناها بدون تماس آنها با يکديگر را القای بارالکتريکی گويند و بارهای ايجاد شده را بار القايی گويند.

اصل پايستگی بار الکتريکی (قانون بقای بار)

براثر مالش دو جسم به يکديگر، بار الکتريکی آفريده يا نابود نمی شود، بلکه مقداری بار از يک جسم به جسم ديگر منتقل می شود و دو جسم باردار می شوند ولی بار کل دو جسم ثابت می ماند.

الکتروسکوپ (برق نما)

وسيله ای است متشکل از يک کلاهک فلزی که يک ميله فلزی به آن متصل است و در سر ديگر ميله دو ورقه ی نازک فلزی (يا يک ورقه) قرار دارد. که ميله و ورقه ها در يک ظرف شيشه ای قرار دارند.

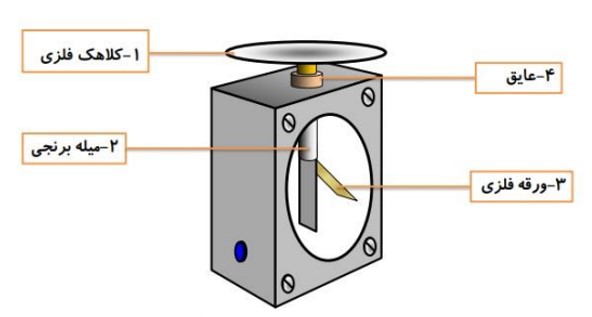
هر گاه به الکتروسکوپ باردار، يک جسم باردار، دارای بار همنام با الکتروسکوپ را به آرامی نزديک کنيم، انحراف ورقه های الکتروسکوپ بيشتر می شود. هر گاه به الکتروسکوپ باردار، جسمی با بار غيرهمنام الکتروسکوپ را به آرامی نزديک کنيم، ورقه های الکتروسکوپ بسته و دوباره باز می شوند. هر گاه جسم خنثی به الکتروسکوپ باردار نزديک کنيم، ورقه ها ابتدا بسته و سپس باز می شوند. هر گاه جسم بدون باری را به کلاهک الکتروسکوپ باردار تماس دهيم، اگر انحراف ورقه ها تغيير محسوسی نکند، جسم نارساناست و اگر انحراف ورقه ها کم شود و يا حتی از بين برود، جسم رساناست.

جزوات جامع پایه ریاضی

جزوه جامع فیزیک (2) رشته ریاضی فصل 1 الکتریسیتۀ ساکن

جزوه جامع فیزیک (2) رشته ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم

جزوه جامع فیزیک (2) رشته ریاضی فصل 3 مغناطیس

جزوه جامع فیزیک (2) رشته ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب

میدان الکتریکی

در فضای اطراف هر جسم باردار خاصيتی بوجود می آيد، که هر گاه جسم باردار ديگری در آن فضا قرار گيرد تحت تاثير قرار می گيرد، به اين خاصيت ميدان الکتريکی می گويند.

تعريف کمی ميدان الکتريکی

نيروی وارد بر يکای بار الکتريکی مثبت را در هر نقطه، ميدان الکتريکی در آن نقطه می ناميم. ميدان الکتريکی بار q در محل بار \({q_0}\) برابر است با: \(E = \frac{F}{{{q_0}}}\)

ميدان الکتريکی کميتی برداری است که آن را با نماد E نشان می دهند و يکای آن در SI، نیوتن بر کولن (\(\frac{N}{C}\) ) است.

مثال

بر بار الکتریکی \(20\mu c\) در یک میدان نقطه از میدان بار q، نیروی \(50 \times {10^{ - 2}}N\) وارد می شود؛ اندازه میدان الکتریکی را در این نقطه محاسبه کنید.

\(\begin{array}{l}{q_0} = 20\mu c = 20 \times {10^{ - 6}}C\\F = 50 \times {10^{ - 2}}N\\E = ?\\E = \frac{F}{{{q_0}}} \to E = \frac{{50 \times {{10}^{ - 2}}}}{{20 \times {{10}^{ - 6}}}} \to E = 2/5 \times {10^4}\frac{N}{C}\end{array}\)

میدان الکتریکی حاصل از ذره باردار

بنا بر قانون کولن نيروی F وارد بر اين بار برابر است با:

\(E = K\frac{{\left| q \right|}}{{{r^2}}}\)

مثال

اندازه و جهت میدان الکتریکی بار ذره \( - 2\mu c\) را در نقطه ای به فاصله \(3cm\) از بار را پیدا کنید.

\(\begin{array}{l}q = - 2\mu c = - 2 \times {10^{ - 6}}C\\r = 3cm = 3 \times {10^{ - 2}}m\\E = ?\\K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\\E = K\frac{{\left| q \right|}}{{{r^2}}} \to E = \frac{{9 \times {{10}^9} \times \left| { - 2 \times {{10}^{ - 6}}} \right|}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}}\\ \to E = \frac{{18 \times {{10}^{ + 3}}}}{{9 \times {{10}^{ - 4}}}} \to E = 2 \times {10^7}\frac{N}{C}\end{array}\)

1 اگر بار الکتریکی q در یک میدان الکتریکی E قرار گیرد، این میدان بر بار q نیروی \(F = q \times E\) را وارد می کند.

2 جهت نیروی F اگر موافق جهت میدان باشد، مثبت و اگر مخالف جهت میدان باشد، منفی است.

مولد وان دو گراف

دستگاهی است که بار الکتریکی روی کلاهک فلزی آن انباشته می شود. اگر یک جسم رسانا با کلاهک این دستگاه تماس پیدا کند دارای بار الکتریکی می شود.

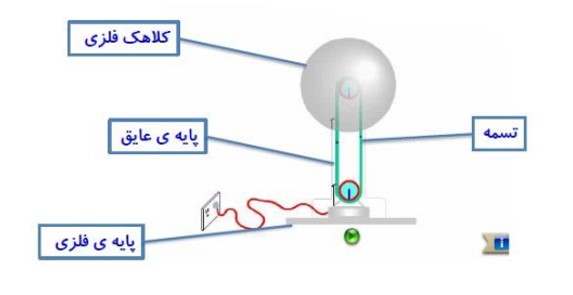
این دستگاه دارای دو غلتک از جنس متفاوت است که توسط تسمه ای به حرکت در می آیند. با حرکت تسمه بار های الکتریکی به کلاهک منتقل می شوند. نوع بار الکتریکی بستگی به جنس غلتک ها دارد.

اصل برهم نهی ميدان های الکتريکی

ميدان الکتريکی ناشی از چند بار الکتريکی در نقطه ای از فضا، برابر مجموع ميدان هايی است که هر بار در نبود ساير بارها در آن نقطه از فضا ايجاد می کند.

\(E = {E_1} + {E_2} + {E_3} + ...\)

گام های اساسی حل مسائل بر هم نهی ميدان الکتريکی

اندازه ميدان الکتريکي ناشی از تک تک بارها را در نقطه مورد نظر محاسبه می کنيم.
جهت ميدان الکتريکی هر بار را در نقطه مورد نظر رسم می کنيم.
اندازه و جهت ميدان برآيند را محاسبه می کنيم.

مثال

شکل زیر، آرایشی از دو بار الکتریکی هم اندازه و غیر همنام (دو قطبی الکتریکی) را نشان می دهد که در آن فاصله دو بار از هم \(6cm\) است. میدان الکتریکی خالص را در نقطه O به دست آورید.

(\(K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\) )

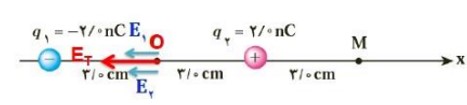
\(\begin{array}{l}{E_1} = \frac{{9 \times {{10}^9} \times \left| { - 2 \times {{10}^{ - 9}}} \right|}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} = \frac{{18}}{{9 \times {{10}^{ - 4}}}} \to {E_1} = 2 \times {10^4}\frac{N}{C}\\{E_2} = \frac{{9 \times {{10}^9} \times 2 \times {{10}^{ - 9}}}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} = \frac{{18}}{{9 \times {{10}^{ - 4}}}} \to {E_2} = 2 \times {10^4}\frac{N}{C}\\{E_T} = {E_1} + {E_2} \to {E_T} = 2 \times {10^4} + 2 \times {10^4} = 4 \times {10^4}\frac{N}{C}\end{array}\)

تجسم ميدان الکتريکی

برای تجسم ميدان الکتريکی در فضای اطراف هر جسم بارداری از خط های ميدان الکتريکی استفاده می شود. ويژگی های اين خطوط عبارتند از:

خط های ميدان در هر نقطه، هم جهت با نيروی وارد بر بار مثبت (بار آزمون) واقع در آن نقطه است. در نتيجه، جهت اين خط ها از بار مثبت به طرف خارج و به سوی بار منفی
مماس بر هر خط ميدان در هر نقطه دلخواه، راستای E در آن نقطه را نشان می دهد. سوی خط ها سوی ميدان الکتريکی است.
خطوط ميدان بايد طوری رسم شوند که تعداد آنها در واحد سطحی عمود بر خط های ميدان با بزرگی E متناسب باشد. به عبارت ديگر هر جا خط های ميدان به هم نزديک تر (متراکم تر) باشند، اندازه E بزرگتر و هر جا که از هم دورتر باشند، اندازه E کوچک تر است.
خط های ميدان يکديگر را قطع نمی کنند، يعنی از هر نقطه دلخواه در فضای اطراف يک يا چند جسم باردار فقط يک خط ميدان می گذرد که همان ميدان الکتريکی برآيند است.

1 ميدان بر سطح رسانا عمود است.

2 ميدان در داخل رسانا صفر است.

خطوط میدان الکتریکی اطراف بار مثبت

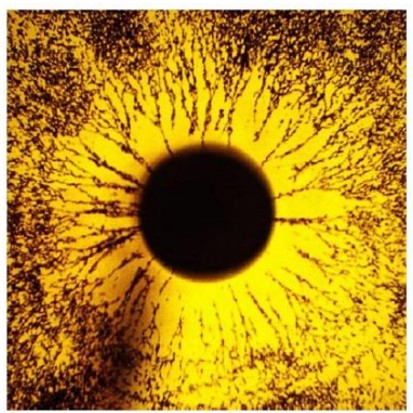
خطوط میدان الکتریکی اطراف بار مثبت و منفی

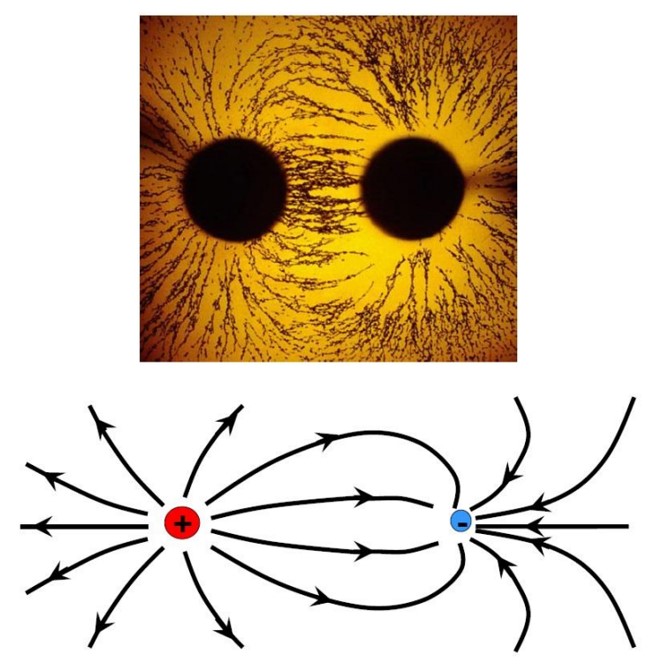
میدان الکتریکی یکنواخت

ميدان الکتريکی را يکنواخت می نامند، که در فضای بين دو صفحه ی رسانا و دور از لبه های صفحات، خطوط ميدان مستقيم، موازی و هم فاصله اند؛ يعنی بردار ميدان در تمام نقاط بين دو صفحه هم اندازه و هم جهت است.

آزمايش قطره روغن ميليکان

اين آزمايش نشان می دهد که بار الکتريکي کميتی کوانتيده است (\(q = \pm ne\) ) .ميليکان بين دو صفحه فلزی موازی و افقی ميدان الکتريکی يکنواخت E را توسط يک منبع ولتاژ قابل تنظيم ايجاد کرد. او در مرکز ورقه ی بالايی چند سوراخ ريز ايجاد کرد که از طريق اين سوراخ ها، قطرات روغن حاصل از يک روغن پاش به ناحيه بين دو ورقه مي پاشيد. بيشتر اين قطره ها در اثر مالش با دهانه خروجی روغن پاش باردار می شدند. ميليکان با تغيير دادن ميدان الکتريکی بين صفحات و با در نظر گرفتن مقاومت هوا، نيروی الکتريکی وارد بر هر قطره را محاسبه کرد و از آنجا بار الکتريکی هر قطره را تعيين کرد.

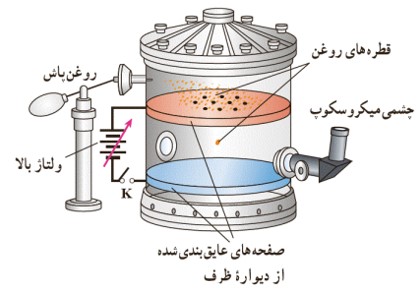
بررسی حرکت بار الکتريکی در ميدان الکتريکی يکنواخت

در يک ميدان الکتريکی يکنواخت قائم، اگر صفحه پايينی منفی باشد بار منفی به حال تعادل درمی آيد و اگر صفحه پايينی مثبت باشد، بار مثبت به حال تعادل درمی آيد و شرط تعادل به صورت زير است.

\({F_E} = W \to Eq = mg\)

شتاب ذره ی باردار، با فرض ناچيز بودن نيروی گرانش از رابطه زير محاسبه می شود.

\(\alpha = \frac{F}{m} = \frac{{Eq}}{m}\)

انرژی پتانسیل الکتریکی

انرژی پتانسيل گرانشی

هميشه ذرهای به جرم m در ميدان گرانشی زمين سقوط می کند، يعنی از پتانسيل گرانشی بيشتر به پتانسيل گرانشی کمتر حرکت می کند.

انرژی پتانسيل الکتريکی

هميشه ذره ای با بار \( + q\) در میدان الکتريکی قائم رو به پايين سقوط می کند، يعنی از پتانسيل الکتريکی بيشتر به پتانسيل الکتريکی کمتر حرکت می کند.

1 رفتار ذره ی باردار، با بار مثبت در ميدان الکتريکی؛ همانند رفتار ذرهای به جرم m در میدان گرانشی زمين است.

2 هر گاه حرکتی، خود به خودی رخ دهد، از پتانسيل (گرانشی – الکتريکی) بيشتر به پتانسيل کمتر مي رود و انرژی پتانسيل (گرانشی – الکتريکی) آن کاهش می يابد.

3 هر گاه در جهت خطوط ميدان (گرانشی – الکتريکی) جابجا شويم، پتانسيل (گرانشی – الکتريکی) مستقل از نوع بار الکتريکی کاهش می يابد.

تغيير انرژی پتانسيل الکتريکی يک ذره ی باردار در ميدان الکتريکي E در يک جابجايی مشخص برابر با منفی کار انجام شده توسط نيروی الکتريکی در همان جابجايی است.

\(\Delta U = - {W_E} = - \left| q \right|Ed.\cos \alpha \)

تغيير انرژی پتانسيل الکتريکی يک ذره ی باردار در ميدان الکتريکی E در يک جابجايی مشخص برابر با مثبت کار انجام شده توسط نيروی عامل خارجی در همان جابجايی است.

\(\Delta U = + W\)

\(\Delta U = + W = - {W_E}\)

هر گاه بار الکتريکی به طرف صفحه همنام حرکت کند، انرژی پتانسيل الکتريکی افزايش می يابد؛ هر گاه به طرف صفحه غير همنام حرکت کند انرژی پتانسيل الکتريکی آن بار کاهش می يابد

اگر کاری که برای جايجايی بار الکتريکی (با سرعت ثابت) انجام می دهيم مثبت باشد (\(W\rangle 0\) ) انرژی پتانسيل الکتريکی بار افزايش می يابد (\(\Delta U\rangle 0\) ) در نتيجه: \({U_2}\rangle {U_1}\)

اگر کاری که برای جايجايی بار الکتريکی (با سرعت ثابت) انجام می دهيم منفی باشد (\(W\langle 0\) ) انرژی پتانسيل الکتريکی بار کاهش می يابد (\(\Delta U\langle 0\) ) در نتيجه: \({U_2}\langle {U_1}\)

تغيير انرژی پتانسيل بار الکتريکی به مسير حرکت بستگی ندارد.

اختلاف پتانسيل الکتريکی

اختلاف پتانسيل الکتريکی دو نقطه، برابر تغيير انرژی پتانسيل الکتريکی يکای بار الکتريکی مثبت است، وقتی يکای بار از نقطه اول تا نقطه دوم جا به جا شود.

بنابراين اگر انرژی پتانسيل الکتريکی بار مثبت q در يک نقطه برابر \({U_1}\) و در نقطه دوم برابر \({U_2}\) باشد، اختلاف پتانسيل الکتريکی بين اين دو نقطه که با نماد \(\Delta V\) نشان داده می شود عبارت است از:

\(\Delta V = \frac{{\Delta U}}{q} \to \Delta V = {V_2} - {V_1} \to \Delta U = {U_2} - {U_1}\)

در این فرمول

(\(\Delta U\) ) بر حسب ژول

(q) بر حسب کولن

(\(\Delta V\) ) بر حسب ولت می باشد.

ولت

يک ولت اختلاف پتانسيل بين دو نقطه از ميدان الکتريکی است که برای جابجا کردن يک کولن بار الکتريکی، يک ژول کار انجام دهيم.

اثبات رابطه \(V = Ed\) در يک ميدان الکتريکی يکنواخت:

اگر فاصله ميان صفحات يک ميدان يکنواخت را با d نشان دهيم و ذره ی باردار در راستای خطوط ميدان الکتريکی حرکت کند، آنگاه داریم:

\(\Delta V = \frac{{\Delta U}}{q} = \frac{{qEd.\cos (0)}}{q} = Ed\)

1 از رابطه \(E = \frac{V}{d}\) می فهميم که واحد ميدان الکتريکی \(\frac{V}{m}\) می باشد. يعنی \(1\frac{V}{m} = 1\frac{N}{C}\)

2 اگر بار الکتريکی مثبت در جهت ميدان الکتريکی حرکت کند، انرژی پتانسيل الکتريکی آن کاهش می يابد. تغيير پتانسيل الکتريکی به تغيير انرژی پتانسيل الکتريکی بستگی دارد.

3 هرگاه بار الکتريکی مثبت در جهت ميدان الکتريکی جا به جا شود، از پتانسيل الکتريکی بيشتر به پتانسيل کمتر رفته است و هرگاه بار الکتريکی مثبت در خلاف جهت ميدان حرکت کند، از پتانسيل الکتريکی کمتر به پتانسيل الکتريکی بيشتر رفته است.

4 هرگاه بار الکتريکی منفی در خلاف جهت ميدان الکتريکی جابجا شود، از پتانسيل الکتريکی کمتر به بيشتر رفته است و هرگاه در جهت ميدان الکتريکی جا به جا شود، از پتانسيل الکتريکی بيشتر به کمتر رفته است.

5 معمولا پتانسيل زمين را صفر در نظر می گيريم و پتانسيل هر جسم را نسبت به آن می سنجيم در اين صورت پتانسيل هر جسم متصل به زمین برابر صفر است.