درسنامه کامل فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
تعداد بازدید : 7.59Mخلاصه نکات فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم - درسنامه شب امتحان فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم - جزوه شب امتحان فیزیک یازدهم ریاضی نوبت اول فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
مدارهای الکتريکی
مدارهای الکتريکی
جريان الکتريکی
ناشی از شارش بارهای متحرک است به عبارت ديگر، عبور بارهای الکتريکی از يک رسانا را جريان الکتريکی گويند.
جهت جريان الکتريکی
جهت حرکت بارهای مثبت، يعنی در خلاف جهت الکترون ها را جهت جريان الکتريکی گويند. (جريان الکتريکی هم جهت با E است.) بنا به قرارداد جهت جريان از قطب مثبت به طرف قطب منفی است.
عامل برقراری جريان، اختلاف پتانسيلی است که در دو سر رسانا اعمال می شود و وسايل توليد اين اختلاف پتانسيل، پيله ای شيميايی، ژنراتورها و . . . هستند.
سرعت سوق
سرعت متوسط شارش الکترون ها در يک رسانا، با اعمال ميدان الکتريکی را که به کُندی حرکت يک حلزون (يعني کمتر از \(1\frac{{mm}}{s}\) ( در خلاف جهت ميدان می باشد، را سرعت سوق می ناميم. اين سرعت باعث ايجاد جريان الکتريکی در يک رسانا می شود.
جريان الکتريکی متوسط
مقدار باری که در واحد زمان از مقطع مداری می گذرد، جريان الکتريکی ناميده می شود و واحد آن آمپر است.
\(I = \frac{{\Delta q}}{{\Delta t}}\)
اگر در تمام بازه های زمانی جهت جريان با زمان تغيير نکند و مقدار جريان ثابت باشد، جريان را مستقيم می نامند، در اين حالت جريان لحظه ای با جريان متوسط برابر است و داريم:
\(I = \frac{q}{t} \to q = It\)
در دستگاه SI، جریان (]) بر حسب آمپر (A)، بار الکتریکی (q) بر حسب کولن (C) و زمان (t) بر حسب ثانیه (s) می باشد.
اگر (I) بر حسب آمپر (A)، و زمان (t) بر حسب ساعت (h) باشد، بار الکتریکی (q) بر حسب آمپر ساعت (Ah) بيان می شود. هر چه آمپر- ساعت يک باتری بيشتر باشد، حداکثر باری که می تواند از مدار عبور دهد تا به طور ايمن تخيله شود، بيشتر است.
\(1Ah = 3600As = 3600C\)
مدار الکتريکی
برای آنکه جريانی برقرار شود، بار الکتريکی به يک مسير بسته نياز دارد تا در آن شارش کند. مسير بسته ای که بارهای الکتريکی در آن حرکت می کنند، مدار الکتريکی ناميده می شود. مدار الکتريکی شامل رساناهای فلزی (سيم يا لامپ)، منبع تامين انرژی الکتريکی (باتری- پيل يا منبع تغذيه) کليد قطع و وصل، وسيله های اندازه گيری اختلاف پتانسيل، شدت جريان و مقاومت الکتريکی (ولت سنج، آمپر سنج و اهم متر يا آوومتر) است. شکل ساده ی مدار الکتريکی در زير رسم شده است.
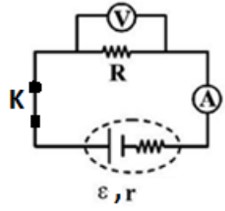
طريقه قرار گرفتن ولت سنج و آمپرسنج در مدار الکتريکی
ولت سنج، وسيله اندازه گيری اختلاف پتاسيل الکتريکی است که به طور موازی در مدار قرار می گيرد و مقاومت آن بسيار زياد می باشد، چون از ولت سنج بايد جريان کمی بگذرد تا ولت سنج اختلاف پتانسيل وسيله مورد نظر را اندازه بگيرد. اگر ولت سنج به صورت متوالی در مدار قرار گيرد، به علت مقاومت زيادی که دارد؛ مانع عبور جريان می شود و جريان شاخه ای از مدار که ولت سنج در آن قرار گرفته است، صفر می شود.
آمپرسنج وسيله اندازه گيری جريان است که بطور سری (متوالی) در مدار قرار می گيرد و مقاومت آن بسيار ناچيز است. زيرا درحد امکان بايد تمام جريان از آمپرسنج بگذرد، تا آمپرسنج جريان آن مصرف کننده را اندازه گيری کند. اگر آمپرسنج به صورت موازی در مدار قرارگيرد، در مدار اتصال کوتاه می شود و آمپرسنج نيز آسيب می بيند.
مقاومت الکتريکی (R)
هنگامی که اختلاف پتانسيلی در دو سر سيم ايجاد شود و باعث حرکت الکترون های آزاد در سيم مدار شود، اين الکترون ها با اتم های رسانا که در حال نوسان اند؛ برخورد می کنند و اين موضوع باعث گرم شدن رسانا می شود. در واقع هر رسانايی در برابر عبور الکترون های آزاد (جريان الکتريکی) از خود مقاومتی نشان می دهد که معمولا به صورت گرما در اجزای مدار الکتريکی ظاهر می شود و اصطلاحاً می گوييم، رسانا دارای مقاومت الکتريکی است
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
قانون اهم
قانون اهم
در دمای ثابت، نسبت اختلاف پتانسيل دو سر رسانا به جريانی که از آن می گذرد، مقدار ثابتی است که برابر مقاومت الکتريکی مدار (R) است.
\(R = \frac{V}{I}\)
1 در رابطه قانون اهم، مقاومت الکتريکي مدار (R) بر حسب اهم (\(\Omega \)) ، اختلاف پتانسيل الکتريکی (V) بر حسب ولت (v) و جريان الکتريکی (I) بر حسب آمپر (A) می باشد.
2 وسايل زيادی وجود دارند که از قانون اهم پيروی نمی کنند، يکی از آنها ديود نور گسيل (LED) است.
تعريف اهم
يک اهم، مقاومت سيمی است که اگر اختلاف پتانسيل يک ولت در دو سر آن برقرار شود، جريان \(1A\) از سيم عبور کند.
\(1\Omega = \frac{{1v}}{{1A}}\)
نمودار قانون اهم
نمودار قانون اهم، خط راستی است که از مبدأ مختصات می گذرد.
اگر محور عمودی را (V) بناميم و محور افقی را (I) بناميم، شيب اين خط برابر مقاومت الکتريکی رسانا است.
اگر محور عمودی را (I) بناميم و محور افقی را (V) بناميم، شيب اين خط برابر عکس مقاومت الکتريکی رسانا است.
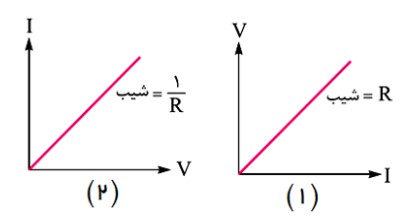
\(\begin{array}{l}1)\tan \alpha = \frac{V}{I} = R\\2)\tan \alpha = \frac{I}{V} = \frac{1}{R}\end{array}\)
با افزايش ولتاژ، در يک دمای ثابت جريان الکتريکی به همان نسبت زياد می شود، اما مقاومت سيم عوض نمی شود.
مثال
بار الکتریکی \(60C\) در مدت زمان \(30s\) از مقطع مداری با اختلاف پتانسیل \(100V\) می گذرد، مقاومت الکتریکی آن را بدست آورید.
\(\begin{array}{l}q = 60C\\t = 30s\\V = 100v\\I = ?\\R = ?\\I = \frac{q}{t} \to I = \frac{{60}}{{30}} = 2\\R = \frac{V}{I} = \frac{{100}}{2} = 50\Omega \end{array}\)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک یازدهم ریاضی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم ریاضی فصل 3 مغناطیس
جزوه جامع فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب
عوامل موثر بر مقاومت الکتریکی
عوامل موثر بر مقاومت الکتریکی
مقاومت يک سيم در دمای ثابت، به عوامل ساختمانی اش از جمله طول، مساحت مقطع و جنس آن بستگی دارد. اگر سطح مقطع سيم در تمام طول آن ثابت باشد، مقاومت آن از رابطه ی \(R = \rho \frac{L}{A}\) بدست می آید.
در این رابطه \(\rho \)، مقاومت ويژه رساناست و به جنس سيم بستگی دارد، واحد آن (\(\Omega m\) ) است؛ L طول سیم بر حسب متر، A سطح مقاومت سیم بر حسب متر مربع است.
ديد ديگر درباره عوامل موثر بر مقاومت الکتريکی
هر چه طول رسانا بيشتر باشد، الکترون ها هنگام عبور از آن برخوردهای بيشتری با اتم ها دارند، بنابراين مقاومت الکتريکی جسم بيشتر می شود. کوچکتر شدن سطح مقطع جسم باعث کاهش عبور جريان از سيم می شود و اين به معنای افزايش مقاومت در برابر عبور جريان است.
1 مقاومت ويژه يک ماده به ساختار اتمی و دمای آن بستگی دارد، رساناهای الکتريکی خوب مقاومت ويژه بسيار کم و عايق های خوب مقاومت ويژه بسيار زيادی دارند. ژرمانيم و سيليسيم که مقاومت ويژه آن ها بين مقاومت ويژه رساناها و نارسانا است را نيمه رسانا می ناميم مقاومت ويژه نيمه رساناها با افزايش دما کاهش می يابد.
2 نسبت مقاومت دو ميله رسانا از رابطه زير بدست می آيد.
\(\frac{{{R_1}}}{{{R_2}}} = \frac{{{\rho _1}}}{{{\rho _2}}} \times \frac{{{L_1}}}{{{L_2}}} \times \frac{{{A_2}}}{{{A_1}}}\)
اثر دما بر مقاومت ويژه رساناهای فلزی و نيم رساناها
در اثر افزايش دمای يک رسانای فلزی، تعداد حامل های بار (الکترون های آزاد) تقريباً ثابت می ماند، ولی ارتعاشات کاتوره ای اتم ها و يون های آن افزايش می يابد. اين عامل موجب افزايش برخورد حامل های بار با شبکه اتمی رسانای فلزی می شود. و به اين ترتيب مقاومت رسانا در برابر عبور جريان زياد می شود. مثلا مقاومت لامپ معمولی روشن با رشته تنگستن از لامپ خاموش مشابه آن بيشتر می باشد؛ آزمايش نشان می دهد مقاومت ويژه فلزات در يک گستره دمايی نسبتاً بزرگ با دما تقريباً به طور خطی تغيير می کند. بر اثر تغيير دما به اندازه ی \(\Delta T\) مقاومت سيم \({R_1}\) برابر \({R_2}\) می شود.
تغیرات مقاومت به صورت \(\Delta R = {R_1}\alpha \Delta T\) نوشته می شود؛ (\(\alpha \)، ضریب دمایی مقاومت است، برای فلزات \(\alpha \rangle 0\) و برای نیم رسانا ها \(\alpha \langle 0\) می باشد.)
1 درصد تغيير مقاومت برای يک سيم به صورت \(\frac{{\Delta R}}{{{R_1}}} \times 100 = \alpha \Delta T \times 100\) نوشته می شود.
2 تغييرات مقاومت ويژه توسط رابطه روبرو بيان می شود. \(\Delta \rho = {\rho _0}\alpha (T - {T_0}) = {\rho _0}\alpha \Delta T\) و یا \(\rho = {\rho _0}\left[ {1 + \alpha (T - {T_0})} \right]\)
اثر دما بر مقاومت ويژه نيم رساناها
در دماهای پايين تعداد حامل های بار نيم رساناها ناچيز است، و نيم رسانا مانند نارسانا رفتار می کند. با افزايش دما بر تعداد اين حامل های بار افزوده می شود؛ گرچه با افزايش دما بر تعداد حامل های بار افزوده می شود و تعداد برخوردهای کاتوره ای نيز افزايش می يابد، اما تأثير افزايش تعداد حامل های بار بيشتر از افزايش اين برخوردهای کاتوره ای است. بنابراين با افزايش دما مقاومت ويژه نيم رسانا کاهش می يابد.
ضريب دمايی مقاومت ويژه برای رساناها مثبت و برای نيم رساناها منفی است، بنابراين مقاومت رساناها با افزايش دما، افزايش می يابد و مقاومت نيم رساناها با افزايش دما، کاهش می يابد.
مثال
ضريب دمايي مس در دماي \(20{}^0C\) برابر با \(0/007{}^0{C^{ - 1}}\) است. اگر مقاومت سیمی مس در دمای \(20{}^0C\) برابر \(5\Omega \) باشد، مقاومت این سیم در دمای \(100{}^0C\) چقدر است؟
\(\begin{array}{l}\Delta R = {R_1}\alpha \Delta T \to \Delta R = 5 \times 7 \times {10^{ - 3}} \times 80 \to \Delta R = 2/8\Omega \\\Delta R = {R_2} - {R_1} \to 2/8 = {R_2} - 5 \to {R_2} = 7/8\Omega \end{array}\)
انواع مقاومت ها
انواع مقاومت ها
مقاومت ها برای کنترل جريان ولتاژ در وسايل الکترونيکی بکار می روند. اندازه ی مقاومت ها می تواند کمتر از \(1\Omega \) تا مگا اهم باشد. انواع اصلی مقاومت ها بر دو نوع است؛ مقاومت های پیچه ای و مقاومت های ترکیبی
مقاومت های پیچه ای
شامل پيچه ای از يک سيم نازک هستند که معمولا جنس آنها از آلياژهايی مانند نيکروم (نيکل- کروم) يا منگانين (مس-نيکل- منگنز) است. اين پيچه ها به دور هسته ای از جنس سراميک، پلاستيک يا شيشه پيچيده شده اند و در غلافی از سراميک قرار گرفته اند.
مقاومت های پيچه ای، قديمی ترين نوع مقاومت هاست که امروزه همچنان توليد می شوند، زيرا می توانند برای حصول مقاومت های پايين بسيار دقيق و همچنين توان های بالا ساخته شوند.
یکی از معروفترين مقاومت های پيچه ای، رئوستا نام دارد که در مدارهای الکتريکی پتانسيومتر ناميده می شود.
رئوستا يا مقاومت تغيير
در آزمايشگاه برای تنظيم و کنترل جريان از يک مقاومت متغير استفاده می شود که رئوستا نام دارد. اين وسيله از يک سيم دراز با مقاومت ويژه نسبتاً زياد (تنگستن) تشکيل شده است. اين سيم روی استوانه ای پيچيده شده است. با استفاده از يک دکمه لغزنده که روي ريلی بالای استوانه قرار دارد و انتهای آن با سيم در تماس است می توان قسمت های دلخواه سيم را در مسير جريان قرار داده و مقاومت را به طور دلخواه تغيير داد.
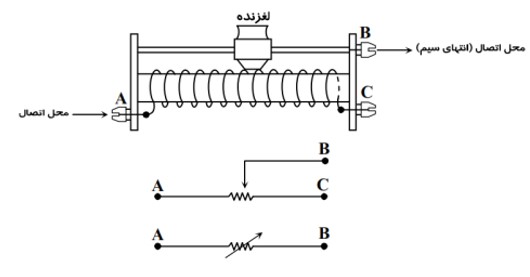
در هنگام استفاده از رئوستا ابتدا آن را با بيشترين مقاومت درمدار قرار می دهيم سپس با دکمه لغزنده، مقاومت مناسب را برای جريان مورد نظر تنظيم می کنيم.
مقاومت های ترکيبی (رنگی)
اين گونه مقاومت ها معمولا از کربن، برخی نيم رساناها، و يا فيلم های نازک فلزی ساخته شده اند که در داخل پوشش پلاستيکی قرار گرفته اند. کارخانه های سازنده اين گونه مقاومت ها، آنها را در اندازه های خاص توليد می کنند. اندازه ی آنها يا بر روی آنها نوشته شده و يا بوسيله ی کدی رنگی نشان داده شده است. مشخصه ی اصلی اين مقاومت ها بيشينه ی توان الکتريکی است که مقاومت ها می تواند بدون آن که بسوزد، تحمل کند.
کد گذاری مقاومت های ترکيبی (مقاومت های کربنی)
در استانداردهای مهندسی، سيم ها را بر حسب قطر و مساحت سطح مقطع آنها نمره بندی می کنند و اندازه ی مقاومت های الکتريکی را با حلقه های رنگی کدگذاری می نمايند. روی مقاومت ها چهار خط رنگی وجود دارد. اگر مقاومت را طوری نگه داريم که در سمت راست، رنگ نقره ای يا طلايی که مشخص کننده ضريب خطا است قرار گيرد، از سمت چپ به ترتيب اولين رنگ، دهگان (a)، دومين رنگ يکان (b) و سومين رنگ، توان 10 (n) می باشند.
\(R = ab \times {10^n}\)
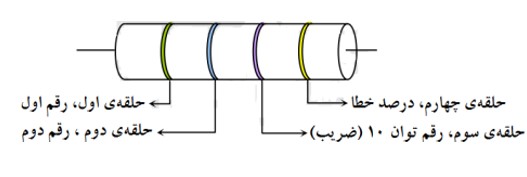
1 دقت کنید اعداد a و b را در هم ضرب نکنید.
2 مقدار خطای حلقه ی چهارم، تلرانس ناميده می شود و ميزان انحراف از مقدار دقيق را بر حسب درصد مشخص می کند.
3 درصد خطای طلایی 5%، درصد خطای نقره ای 10% و درصد خطای بی رنگ 20% است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
مقاومت های خاص
مقاومت های خاص
ترميستور
ترميستور نوعی مقاومت الکتريکی است که وابستگی مقاومت الکتريکی آن به دما، با مقاومت های معمولی متفاوت است. از ترميستور به عنوان حسگر دما در مدارهای حساس به دما مانند زنگ خطر آتش، دماپا و دماسنج استفاده می شود. رايج ترين ترميستورها ديسکی، مهره ای و ميله ای است.
به مقاومت های حساس به دما که از مواد نيمه هادی ساخته می شود، ترميستور می گويند.
در ترميستور مقاومت الکتريکی با دما به طور غير خطی تغيير می کند. رنج دمای آن \( - 70\) تا 150 و نهايتا 316 درجه سانتيگراد می باشد. در اکثر کاربردها مقاومت آن در دمای 25 درجه سانتيگراد بين 100 تا 100 کيلو اهم می باشد.
1 اندازه کوچک، پاسخ سريع, حساسيت بسيار بالا از مزایای ترمیستور ها است.
2 غير خطی، محدوده دمايی کم، شکننده، مقاومت بالا و مشکلات نويز، ناپايداری و کاليبره نبودن از معایب ترمیستور ها است.
مقاومت های نوری (LDR)
نوعی مقاومت است که مقاومت الکتريکی آن به نور تابيده شده به آن بستگی دارد. به طوری که با افزايش شدت نور، از مقاومت آن کاسته می شود. اندازه ی مقاومت های نوری از چند مگا اهم در تاريکی تا چند صد اهم در روشنايی قابل تغيير است.
نوعی از اين مقاومت ها از جنس نيم رسانای خالص، مانند سيليسيم هستند که با افزايش شدت نور تابيده شده، بر تعداد حامل های بار الکتريکي آنها افزوده شده و در نتيجه از مقاومت آنها کاسته می شود. مقاومت الکتريکی چنین LDR هایی را بر حسب روشنایی (LUX) سنجیده می شوند. از (LDR) در چشم های الکترونیکی، دزدگيرها، کنترل کننده های خودکار و چراغ روشنايی خيابان ها استفاده می شود.
ديودها (يکسوکننده جريان)
ديود قطعه ای است که هر گاه در مداری قرار گيرد، حريان را تنها از يک سو عبور می دهد و مقاومت آن در برابر عبور جريان در اين سو ناچيز است. معروف ترين ديودها، ديودهای نوری يا (LED) هستند. از LED در چراغ خودررو، روشنايی منازل، تابلوهای تبليغاتی، نمايشگرهای LED و ... استفاده می شود. LED ها در مقايسه با لامپ رشته ای عمر طولانی تری دارند و به دليل نداشتن رشته سيم در آنها به هنگام توليد نور، گرمای زيادی توليد نمی کنند.
محاسبه انرژی الکتريکی مصرف شده در يک مقاومت
هنگامی که بار مثبت q در جهت ميدان الکتريکی يکنواخت حرکت کند، انرژی پتانسيل الکتريکی آن به اندازه \(q.\Delta V\) کاهش می يابد.
\(\Delta U = q \times \Delta V\)
اين کاهش انرژی پتانسيل به صورت انرژی جنبشی در می آيد. در اثر برخورد اين بارها با اتم ها اين انرژی به اتم های رسانا منتقل می شود و انرژی درونی رسانا را افزايش می دهد، در نتيجه در اثرعبور جريان الکتريکی رسانا گرم می شود.
اگر جريان ثابت I در مدت t ثانيه در سيمی به مقاومت R برقرار شود، داريم:
\(1)U = (It).(RI) = R{I^2}t\)
U: انرژی که بار هنگام عبور از سيم از دست می دهد و به انرژی درونی سيم تبديل می شود.
با توجه به رابطه (1) و رابطه قانون اهم (\(V = RI\) ) روابط ديگری برای انرژی بدست می آوريم:
\(2)U = VIt\)
\(3)U = \frac{{{V^2}}}{R}t\)
توان الکتريکی مصرفی در يک مقاومت (P)
مقدارانرژی مصرف شده در واحد زمان را توان الکتريکی می نامند و با نماد P نشان می دهند.
\(P = \frac{U}{t}\)
1 يکای توان الکتريکی در SI، ژول بر ثانيه است که آنرا وات (W) می نامیم.
2 با توجه به رابطه ی \(U = R{I^2}t = VIt = \frac{{{V^2}}}{R}t\) و رابطه \(P = \frac{U}{t}\) ، رابطه های زير برای توان الکتريکی مصرف شده در مقاومت به دست می آيد.
\(P = R{I^2} = VI = \frac{{{V^2}}}{R}\)
توان و انرژی الکتريکی مصرفی يا (گرما) در مقاومت
برای محاسبه انرژی الکتريکی مصرفی يا گرمای توليد شده توسط يک مقاومت کافيست که توان آن مقاومت را در زمان ضرب کنيد، \(U = P \times t\) . دقت کنيد؛ توان، انرژی الکتريکی مصرفی کل مدار را می توان به دو شکل حساب کرد.
راه اول: برای هر مقاومت حساب کرد و بدون توجه به جايگاهشان همگی را با هم جبری جمع کرد.
راه دوم: اگر ولتاژ کل يا جريان کل را داشتيم با محاسبه ی مقاومت معادل، از \(P = R{I^2}\) یا \(P = \frac{{{V^2}}}{R}\) استفاده کنيم.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک یازدهم ریاضی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم ریاضی فصل 3 مغناطیس
جزوه جامع فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب
نيروی محرکه الکتريکی و مولدها
نيروی محرکه الکتريکی و مولدها
بارهای الکتريکی ضمن شارش در مدار الکتريکی انرژی جنبشی از دست می دهند،کار مولد اين است که اين انرژی را دوباره تامين کند. همانطور که می دانيم بارهای الکتريکی از پتانسيل پايين تر شارش می کند و وارد مولد می شوند؛ مولد با صرف انرژی بارهای الکتريکی را از پتانسيل پايين تر به پتانسيل بالاتر می برد و سبب شارش آنها در مدار می شود. بارهای الکتريکی هنگام شارش انرژی خود را از دست می دهند برای اينکه شارش بار در مدار تداوم يابد اين انرژی بايد بوسيله مولد تامين شود.
وسيله ای که با انجام کار روی بار الکتريکی اختلاف پتانسيل را ثابت نگه می دارد، منبع نيروی محرکه الکتريکی ناميده می شود.
منبع نيروهای الکتريکی بارهای الکتريکی مثبت را در خلاف جهت ميدان الکتريکی از پتانسيل پايين تر به پتانسيل بالاتر می برند و با افزايش انرژی پتانسيل آنها، جريان ثابتی در مدار برقرار می کنند.
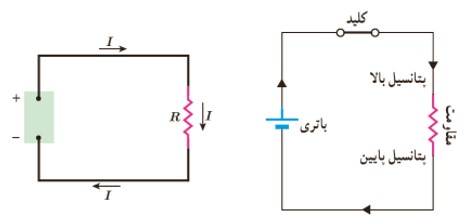
باتری، پيل سوختی، سلول خورشيدی و مولدهايی الکتريکی نمونه هايی از منبع نيروی محرکه الکتريکی اند.
کاری که منبع نيروی محرکه روی واحد بار الکتريکی مثبت انجام می دهد تا آن را از پايانه با پتانسيل کمتر به پايانه با پتانسيل بيشتر ببرد، نيروی محرکه الکتريکی (emf) می نامند.
\(\varepsilon = \frac{{\Delta W}}{{\Delta q}}\)
يکای نيروی محرکه مولد، ژول برکولن (\(\frac{J}{C}\) ) یا ولت (V) است.
منبع نيروهای محرکه الکتريکی يا آرمانی (\(r = 0\) ) و یا واقعی (\(r \ne 0\) ) هستند، در حالت آرمانی اختلاف پتانسيل الکتريکی ميان اين دو پايانه با نيروی محرکه الکتريکی برابر است.
\({V_b} - {V_a} = \varepsilon \)
در حالت واقعی هنگامی جريان از مولد می گذرد، اختلاف پتانسيل بين پايانه های آنها بر خلاف منابع آرمانی، متفاوت از نيروی محرکه الکتريکی خواهد شد، يعنی اختلاف پتانسيل در مقايسه با نيروی محرکه مولد بيشتر و يا کمتر خواهد شد.
هر مولد دارای مقاومت درونی است که آن را با r نمايش می دهند و علامت آن در مدارهای الکتريکی به صورت شکل روبرو است.
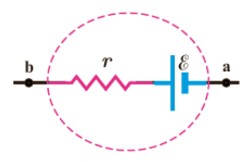
قواعد حل مدارهای تک حلقه ای
در هر دور زدن کامل حلقه ای از مدار، جمع جبری اختلاف پتانسيل های اجزای مدار صفر است.
برای حل مدارهای تک حلقه ای بايد يک جهت دلخواه برای جريان الکتريکی و يک جهت دلخواه برای گردش حلقه در نظر بگيريم. اگر در سوالی جهت جريان و گردش حلقه مشخص باشد، بايد از همان جهت های مشخص پيروی کنيم اين جهت ها ساعتگرد و يا پاد ساعتگردند.
الف) هرگاه روی مداری در جهت جريان از مقاومت R و یا r بگذريم، پتانسيل به اندازه IR یا Ir کاهش می يابد و اگر درخلاف جهت جريان از مقاومت ها بگذريم، پتانسيل به اندازه IR یا Ir افزایش می یابد.
ب) هرگاه برای گذر از مولد (بدون توجه به جهت جريان) از پايانه منفی به پايانه مثبت برويم، پتانسيل به اندازه نيروی محرکه مولد افزايش می يابد و اگر از پايانه مثبت به منفی (بدون توجه به جهت جريان) بگذريم، پتانسيل به اندازه نيروی محرکه مولد کاهش می يابد.
1 برای محاسبه جريان يک حلقه حتماً بايد حلقه را يک دورکامل بگرديم. يعنی بايد از يک نقطه فرضی شروع کنيم و در جهت دلخواه گردش کنيم و هنگام گذر از هر جزء را اضافه کنيم. (اگر اين تغييرات افزايش يابند، با علامت مثبت و اگر کاهش يابند، با علامت منفی جايگذاری می کنيم.(
2 برای محاسبه اختلاف پتانسيل بين دو نقطه از مدار، ابتدا پتانسيل نقطه اول را می نويسيم آنگاه از اين نقطه روی مدار در جهت دلخواه به طرف نقطه دوم می رويم و ضمن گذر از هر جزء تغييرات پتانسيل هر جزء را اضافه می کنيم تا به نقطه دوم برسيم، حاصل برابر پتانسيل نقطه دوم است.
3 اگر درحل مداری جريان بدست آمده مثبت باشد، معلوم می شود که جهت انتخاب شده درست است و اگر جريان بدست آمده منفی باشد، معلوم می شود که جهت جريان در مدار، خلاف جهتی است که انتخاب شده است.
مدار تک حلقه با چند مولد
مولدها وسايلی هستند که انرژی لازم را جهت حرکت الکترون در مدار تامين می کنند. مولدها تمايل دارند جريان را از پايانه مثبت خود خارج کنند، البته در شرايطی که تحت تأثير مولدی قرار بگيرند که از خودشان قوی تر باشد، جريان را از پايانه منفی خود خارج می کنند که در اين صورت به آنها مولدهای مصرف کننده (ضد مولد) نيز می گوييم، توان اين مولدها را توان ورودی ميناميم.
در مدارهای تک حلقه ای که چند مولد در يک شاخه حضور دارد، گام صفر اين است که بر اساس زور سنج ها (\(\varepsilon \)) نيرو محرکه ها جهت جريان را مشخص کنيم، سپس اندازه ی آن را تعيين کنيم.
اندازه ی جريان را در اين گونه حلقه ها، از رابطه ی \(I = \frac{{\sum \varepsilon - \sum {\varepsilon '} }}{{\sum {(R + r)} }}\) بدست می آيد که \(\sum \varepsilon \) مجموع تمام نيروی های محرکه مولد (مولد توليد کننده) و \(\sum {\varepsilon '} \) مجموع تمام نيرومحرکه های ضد مولد (مولد مصرف کننده( هستند.
در مدار روبرو، فرض کنيد ؛ \(({\varepsilon _1} + {\varepsilon _3})\rangle {\varepsilon _2}\)
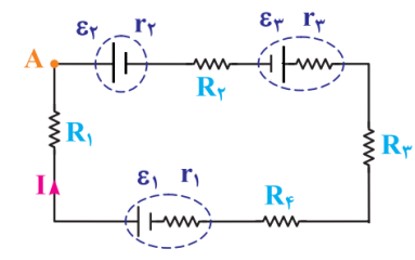
زور نيرو محرکه ی مولدهای ساعتگرد (مولد اول و سوم) از نيرو محرکه های مولدهای پاد ساعتگرد (مولد دوم) بيشتر است.
مولد اول: جريان از سر مثبت خارج شده – پس توليد کننده است.
مولد دوم: جريان به سر مثبتش وارد شده – پس مصرف کننده است.
مولد سوم: جريان از سر مثبت خارج شده – پس توليد کننده است.
\(I = \frac{{({\varepsilon _1} + {\varepsilon _3}) - {\varepsilon _2}}}{{{R_1} + {R_2} + {R_3} + {R_4} + {r_1} + {r_2} + {r_3}}}\)
باتری که جريان از سر مثبتش خارج شود را مولد (يا مولد توليد کننده يا مولد برنده) و باطری که، جريان از سر منفی اش خارج شود؛ را ضد مولد (يا مولد مصرف کننده يا مولد بازنده) می ناميم. اگر در مداری فقط يک باتری داشته باشيم، قطعاً مولد (مولد توليد کننده) است و جريان از سر مثبتش خارج می شود.
مثال
در مدار شکل زیر
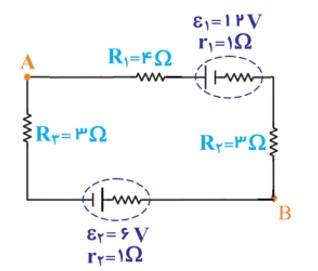
الف شدت جریان چند آمپر است؟
\(\begin{array}{l}{V_A} - i{R_1} - i{r_1} - {\varepsilon _1} - i{R_2} - i{r_2} - {\varepsilon _2} - i{R_3} = {V_A}\\ \to i = \frac{{{\varepsilon _1} + {\varepsilon _2}}}{{{R_1} + {R_2} + {R_3} + {r_1} + {r_2}}} = \frac{{12 + 6}}{{4 + 3 + 3 + 1 + 1}} = \frac{{18}}{{12}} = 1/5V\end{array}\)
ب اختلاف پانسیل دو نقطه ی A و B، (\({V_B} - {V_A}\) ) چند ولت است؟
\({V_B} - {\varepsilon _2} - i{r_2} - i{R_3} = {V_A} \to {V_B} - {V_A} = {\varepsilon _2} + i{r_2} + i{R_3} = 6 + 1/5 \times 1 + 1/5 \times 3 = 12V\)
ج اختلاف پتانسیل باتری (1) را بدست آورید؟
\({V_c} + {\varepsilon _1} - i{r_1} = {V_d} \to {V_d}\rangle {V_c} \to {V_d} - {V_c} = {\varepsilon _1} - i{r_1} = 12 - 1/5 \times 1 = 10/5V\)
اگر نقطه ای از مدار به زمين متصل باشد، پتانسيل آن نقطه برابر صفر در نظر گرفته می شود.
افت پتانسيل در مولد
افت پتانسيل در مولد
مولدهای ايده آل دارای مقاومت درونی نيستند، ولی مولدهای معمولی دارای مقاومت کمی هستند به همين علت مقداری از انرژی داده شده توسط مولد در خود مولد به صورت گرما تلف می شود.
مقدار انرژی مصرف شده توسط واحد بار در داخل مولد را افت پتانسيل مولد می ناميم.
با توجه به مدار مقابل می توان افت پتانسيل در يک مولد را حساب کرد.
در حالتی که جريان از مولد نگذرد (\(Ir = 0\) ) يعني مدار باز باشد، اختلاف پتانسيل دوسر مولد با نيروی محرکه مولد برابر است. بنابراين نيروی محرکه مولد برابر اختلاف پتانسيل دو سر مولد است وقتی که جريانی از مولد نگذرد، پس :
\(1){V_A} - {V_B} = IR = V\)
اگر دو سر مولد را به ولت سنجی متصل کنيم، عملا جريانی از ولت سنج نمی گذرد. عددی که ولت سنج نشان می دهد برابر نيروی محرکه مولد است، از طرفی مطابق شکل بالا و حل مدارهای تک حلقه ای داريم:
\(\begin{array}{l}2){V_A} - \varepsilon + Ir = {V_B} \to {V_A} - {V_B} = \varepsilon - Ir\\3)V = {V_A} - {V_B} = \varepsilon - Ir\end{array}\)
از رابطه (1) و (2) نتيجه می گيريم:
يعنی اختلاف پتانسيل دو سر مولد به اندازه Ir از نيروی محرکه مولد کمتر است.
از رابطه (3) و رابطه (1) می توان شدت جريانی را که از يک مولد می گذرد، حساب کرد. پس:
\(I = \frac{\varepsilon }{{R + r}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
توان در مدارهای الکتريکی
توان در مدارهای الکتريکی
به طور کلی اگر يک عنصر مداری (مقاومت و يا مولد) داری اختلاف پتانسيل \(\Delta V\) باشد، بار \(\Delta q\) در مدت زمان \(\Delta t\) از اين عنصر می گذرد. کار خارجی برای انتقال چنين باری برابر است با:
\(W = \Delta q.\Delta V\)
از طرفی توان الکتريکی برابر است با:
\(P = \frac{{\Delta W}}{{\Delta t}} = \frac{{\Delta q \times \Delta V}}{{\Delta t}} = \left( {\frac{{\Delta q}}{{\Delta t}}} \right) \times \Delta V = I \times \Delta V = I \times \left( {{V_b} - {V_a}} \right)\)
اگر \(P\rangle 0\) باشد، اين عنصر به مدار انرژی می دهد و اگر \(P\langle 0\) باشد، اين عنصر از مدار انرژی می گيرد.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک یازدهم ریاضی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم ریاضی فصل 3 مغناطیس
جزوه جامع فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب
توان مولد
توان مولد
مقدار انرژی مصرف شده در واحد زمان در هر مصرف کننده الکتريکی را توان مصرفی آن می ناميم. اگر جريان I از مولد بگذرد انرژی مصرفی آن عبارت است از:
\(U = \varepsilon It\)
توان توليدی مولد از رابطه \(P = \frac{U}{t} = \varepsilon \times I\) بدست می آید.
بخشی از اين توان توليدی، توسط خود مولد به دليل مقاومت درونی مولد (r) در درون مصرف می شود که بنا به آنچه در مورد يک مقاومت ديديم اين مقدار برابر است با:
\(P' = {I^2}r\)
بنابرين داريم:
توان مفید یا خروجی مولد = توان مصرف شده در مولد – توان تولیدی مولد
يعني توان مفيد مولد (توان خروجی) از رابطه \(P'' = \varepsilon I - {I^2}r\) بدست می آید.
مثال
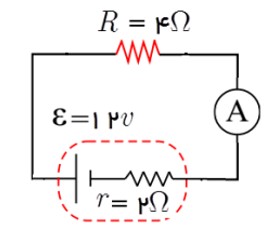
در شکل بالا
الف) توان ذخیره شده در مولد
ب) توان مصرفی مقاومت درونی مولد
ج) توان مصرفی در مقاومت R
الف)
\(I = \frac{\varepsilon }{{R + r}} = \frac{{12}}{{4 + 2}} = 2A,P = \varepsilon I = 12 \times 2 = 24W\)
ب) توان مصرفی درون مولد توسط مقاومت درونی مصرف می شود.
\(P = {I^2}R = {2^2} \times 2 = 8W\)
ج) توان مصرفی مقاومت با توان خروجی مولد برابر است.
\(\begin{array}{l}P = R{I^2} = 4 \times {2^2} = 16W\\P = \varepsilon I - {I^2}r = 12 \times 2 - {2_2} \times 2 = 24 - 8 = 16W\\P'' = P - P' = 24 - 8 = 16W\end{array}\)
معادل گیری مقاومت ها
معادل گیری مقاومت ها
الف) اتصال متوالی مقاومت ها:
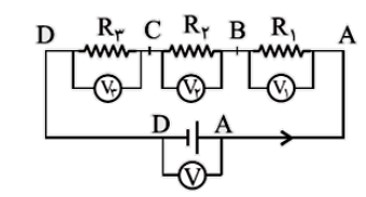
در اين مقاومت ها شدت جريان دو سر هر مقاومت، با شدت جريان کل مدار برابر است. يعنی:
\({I_T} = {I_1} = {I_2} = {I_3} = ...\)
در مقاومت های متوالی اختلاف پتانسيل کل مقاومت ها، برابر مجموع اختلاف پتانسيل تک تک مقاومت هاست. يعنی:
\({V_T} = {V_1} + {V_2} + {V_3} + ...\)
مقاومت معادل، در مقاومت های متوالی برابر مجموع تک تک مقاومت های مدار است.
\({R_T} = {R_1} + {R_2} + {R_3} + ...\)
در اين حالت مقاومت معادل از بزرگترين مقاومت موجود در مجموعه بزرگتر است.
با حذف يک مقاومت که به صورت متوالی در مدار قرار گرفته است، مقاومت مدار کاهش می يابد. در نتيجه بنا به رابطه \(I = \frac{V}{R}\) ، شدت جريان شاخه ای از مدار که آن مقاومت در آن قرار گرفته است افزايش می يابد و بالعکس.
اختلاف پتانسيل کل در مقاومت های سری، به نسبت مقاومت ها توزيع می شود. يعنی هر مقاومتی که بزرگ تر است سهم بيشتری از اختلاف پتانسيل کل را می گيرد.
\({I_1} = {I_2} \to \frac{{{V_1}}}{{{R_1}}} = \frac{{{V_2}}}{{{R_2}}} \to \frac{{{V_1}}}{{{V_2}}} = \frac{{{R_1}}}{{{R_2}}}\)
در حالت متوالی، توان مصرفی با مقاومت الکتريکی رابطه ی مستقيم دارد.
\(\begin{array}{l}{I_1} = {I_2}\\P = R{I^2}\\ \to \frac{{{P_2}}}{{{P_1}}} = \frac{{{R_1}}}{{{R_2}}}\end{array}\)
اگر n مقاومت مشابه با مقاومت \({R_1}\) داشته باشيم،که به طور متوالی بسته شده اند، مقاومت معادل برابر است با:
\({R_T} = n{R_1}\)
در اتصال سری، نبايد از سر مشترک انشعابی خارج گردد؛ شاخه ای که در آن ولت سنج ايده آل، کليد باز، خازن باردار يا مقاومت بی نهايت باشد انشعاب به حساب نمی آيد؛ زيرا مقاومت آنها بی نهايت است و الکترون وارد شاخه ی آنها نمی شود پس جريان در آنها صفر است، بنابراين: سه مقاومت زير سری هستند.
ب) اتصال موازی مقاومت ها
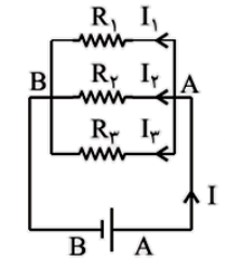
مقاومت هايی را موازی گويند، که دو سر هر يک از آنها به يک نقطه مشترک متصل باشند. در اين اتصال، يک سر همه ی مقاومت ها به يک نقطه و سر ديگر همه ی آنها نيز به يک نقطه ی ديگر متصل است، به همين خاطر اختلاف پتانسيل دو سر همه ی مقاومت ها يکسان است و داريم:
در اين مقاومت ها اختلاف پتانسيل هر مقاومت با اختلاف پتانسيل کل مدار برابر است. یعنی:
\({V_T} = {V_1} = {V_2} = {V_3} = ...\)
شدت جريان کل مدار، با مجموع شدت جريان های عبوری تک تک مقاومت ها برابر است. يعنی:
\({I_T} = {I_1} + {I_2} + {I_3} + ...\)
مقاومت معادل، مقاومت های موازی از رابطه ی زير بدست می آيد.
\(\frac{1}{{{R_T}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} + ...\)
يعنی، وارون مقاومت معادل مقاومت های موازی، برابر مجموع وارون تک تک مقاومت هاست. پس مقاومت معادل از کوچکترين مقاومت موجود در مجموعه کوچکتر است.
اگر يک مقاومت به صورت موازی به مدار اضافه شود، مقاومت مدار کوچک تر می شود و بالعکس، با حذف يک مقاومت موازی، مقاومت معادل بزرگتر می شود.
برای دو مقاومت موازی می توان مقاومت معادل را از رابطه روبرو بدست آورد.
\({R_T} = \frac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}}\)
اگر n مقاومت مشابه \({R_1}\) به صورت موازی به هم بسته شوند، مقاومت معادل آنها برابر است با:
\({R_T} = \frac{{{R_1}}}{n}\)
اگر دو مقاومت با هم موازی باشند، شدت جريان به نسبت عکس مقاومت ها توزيع می شود. يعنی مقاومتی که بزرگتر است جريان کمتری را از خود عبور می دهد.
\({V_1} = {V_2} \to {R_1}{I_1} = {R_2}{I_2} \to \frac{{{R_1}}}{{{R_2}}} = \frac{{{I_1}}}{{{I_2}}}\)
در حالت موازی شاخه ای که مقاومت کمتری دارد، گرمای بيشتری توليد می کند.
\(\begin{array}{l}{V_1} = {V_2}\\P = \frac{{{V^2}}}{R}\\ \to \frac{{{P_2}}}{{{P_1}}} = \frac{{{R_1}}}{{{R_2}}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی



1736019749.png)















