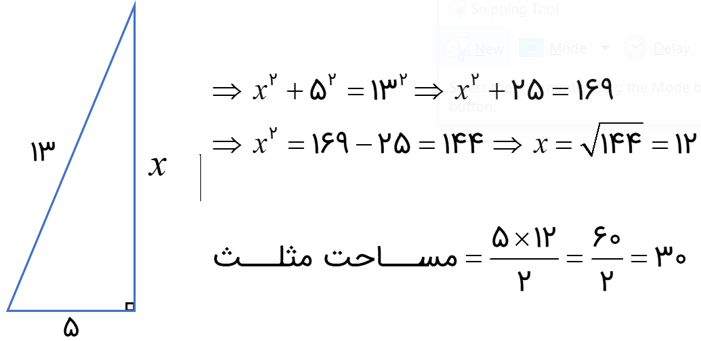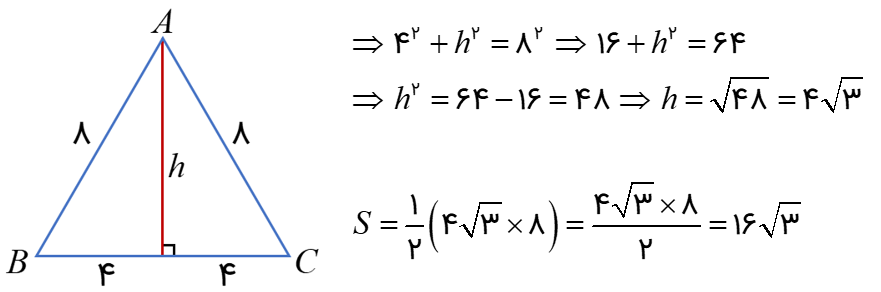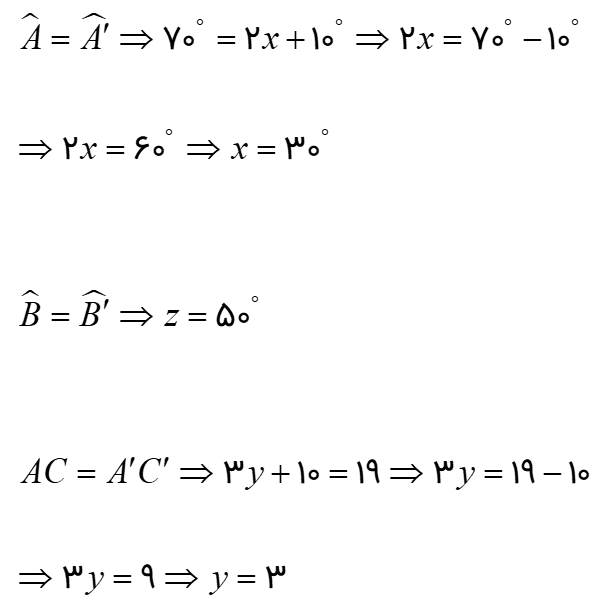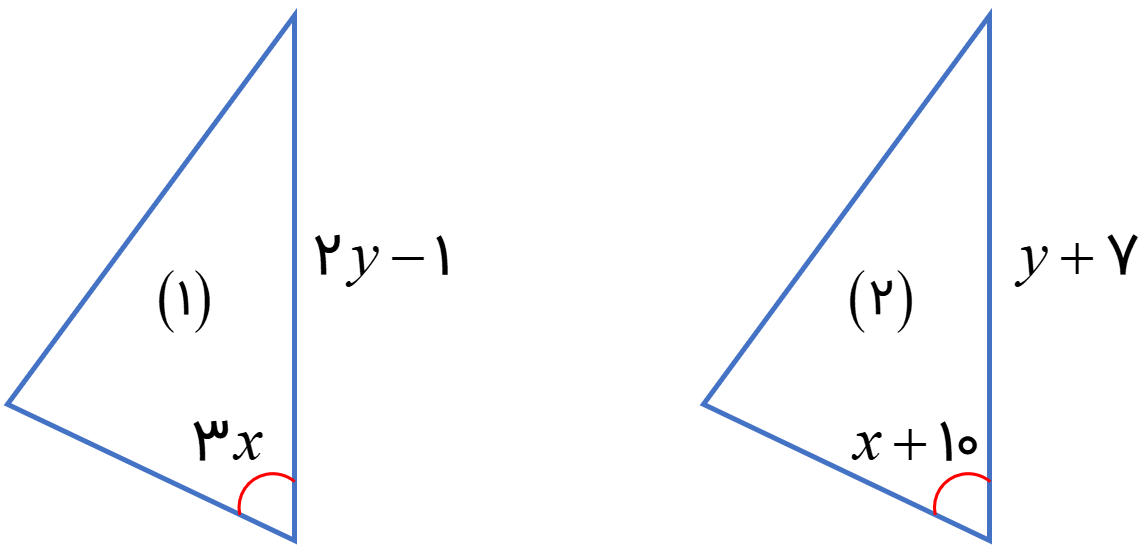در مثلث قائم الزاویه ABC، c طول وتر و a و b طول اضلاع قائمه هستند. مقدار مجهول را در هر قسمت بیابید.
\(\begin{array}{l}1)\,a = 12\,\,,\,\,c = 20\,\,\, \Rightarrow \,\,\,b = ?\\\\2)\,a = 3\,\,,\,\,b = 4\,\,\, \Rightarrow \,\,\,c = ?\\\\3)\,b = 5\,\,,\,\,c = 10\,\,\, \Rightarrow \,\,\,a = ?\end{array}\)
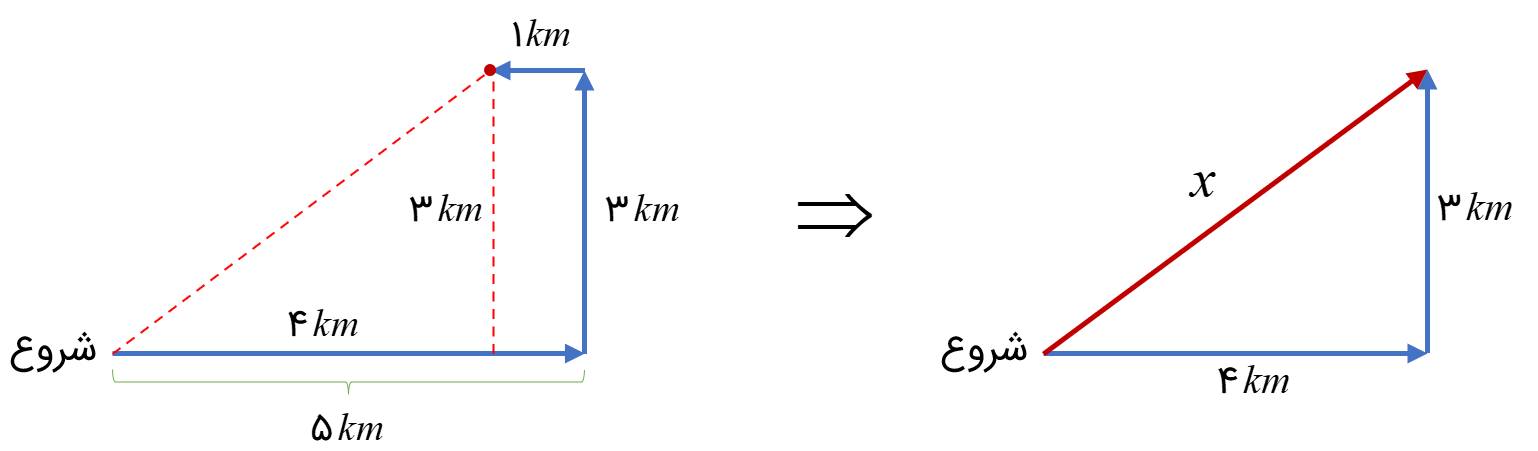
شخصی 5 کیلومتر به سمت شرق، 3 کیلومتر به سمت شمال و 1 کیلومتر سمت غرب می رود. او در چه فاصله ای از نقطه شروع است؟
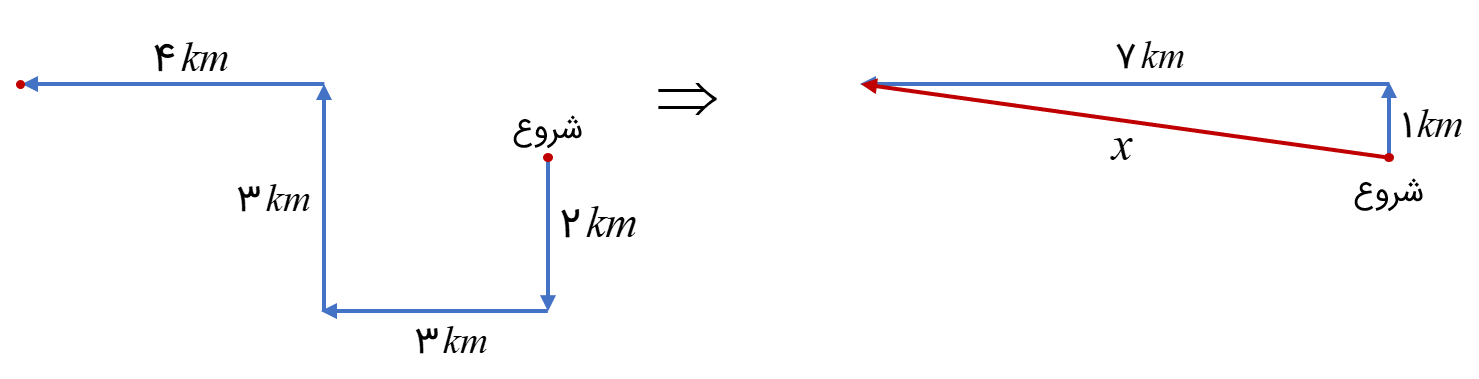
شخصی 2 کیلومتر به سمت جنوب، 3 کیلومتر به سمت غرب، 3 کیلومتر سمت شمال و در نهایت 4 کیلومتر به سمت غرب می رود. او در چه فاصله ای از نقطه شروع نقل مکان کرده است؟
وتر یک مثلث قائم الزاویه 13 و طول یک ضلع آن 5 است. مساحت مثلث را بیابید.
کدام سه عدد می تواند طول اضلاع یک مثلث قائم الزاویه باشند؟
\(\begin{array}{l}1)\,4\,,\,4\,,\,4\sqrt 2 \\\\2)\,3\,,\,4\,,\,5\\\\3)\,6\,,\,7\,,\,9\end{array}\)
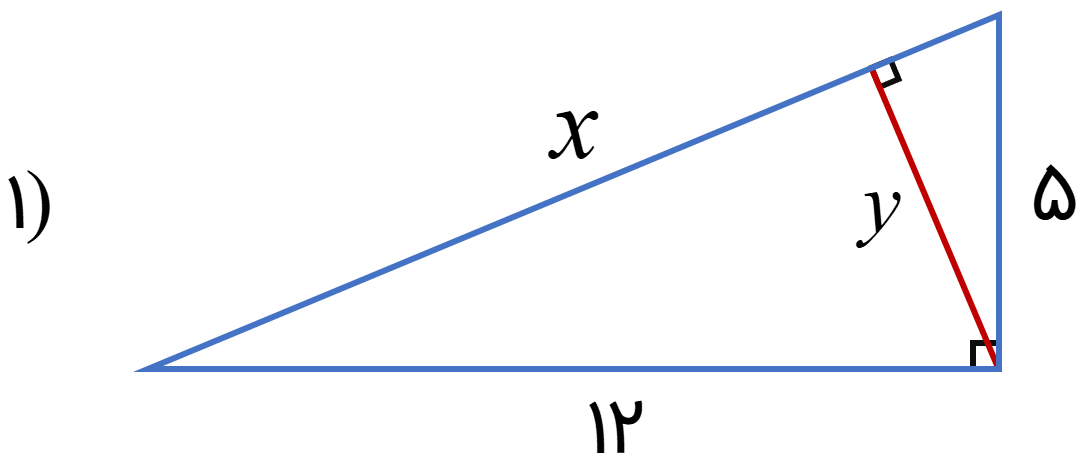
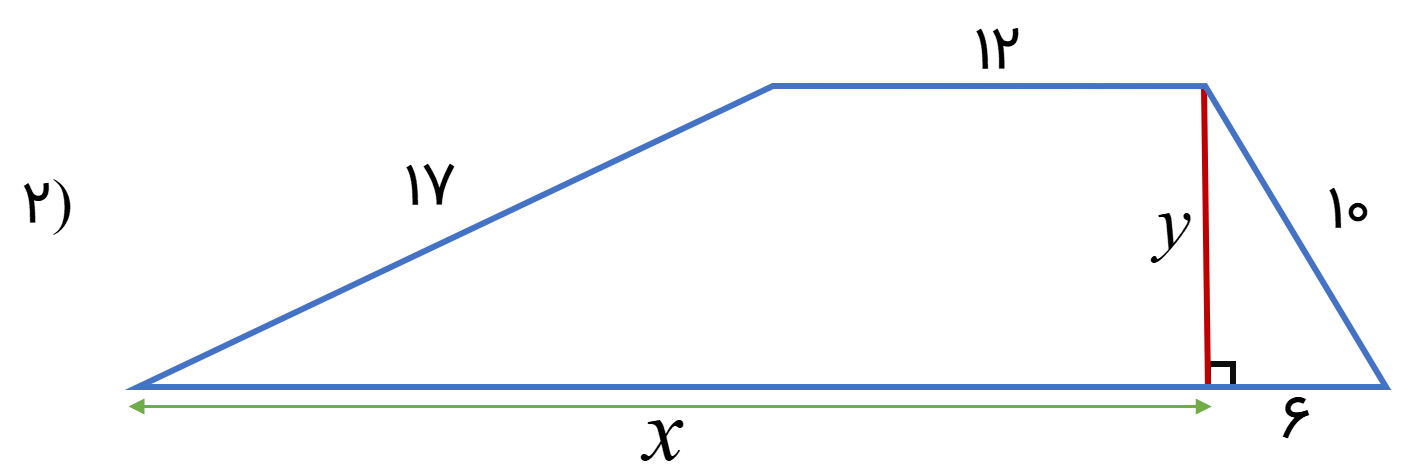
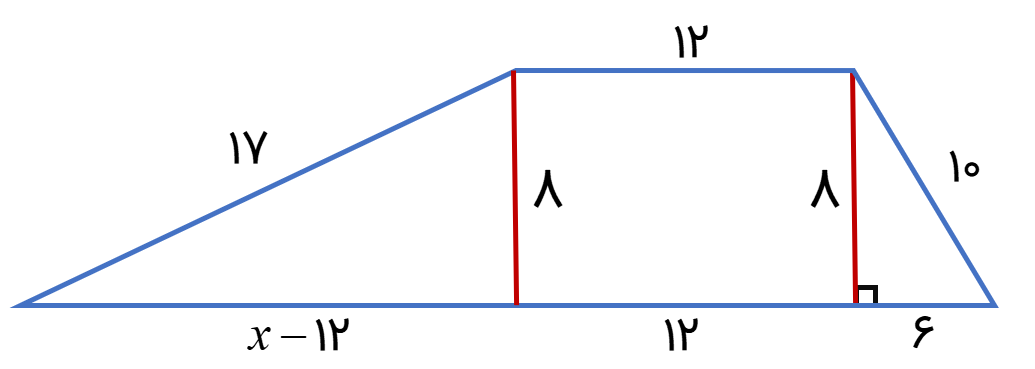
در هر قسمت با توجه به شکل مقادیر مجهول را بیابید.
مساحت مثلث متساوی الاضلاع به ضلع 8 را بدست آورید.
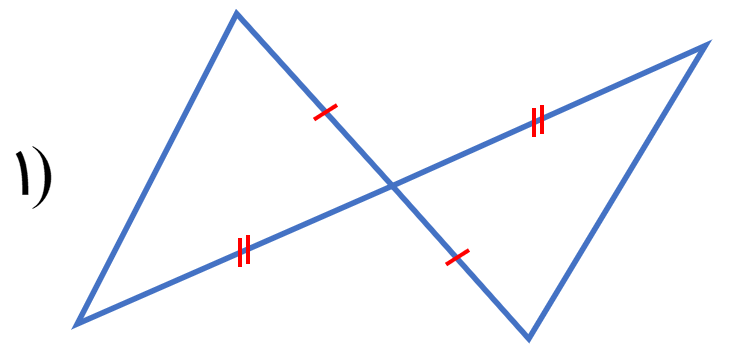
جفت شکل های هم نهشت را مشخص کنید.
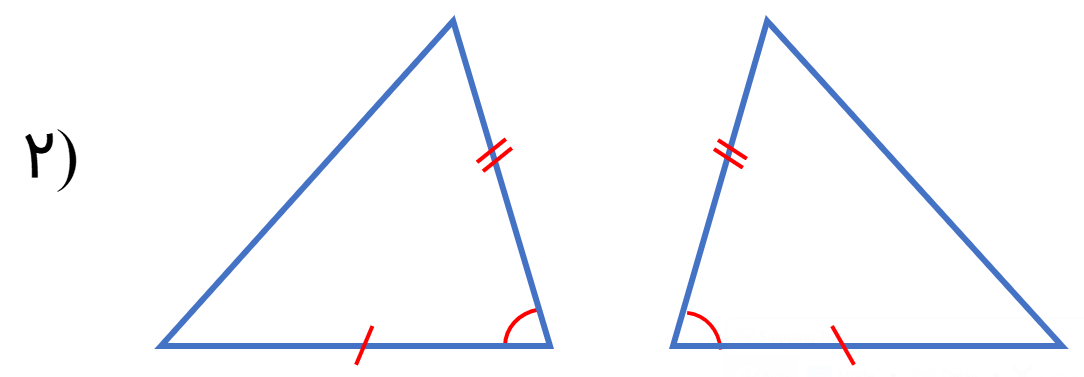
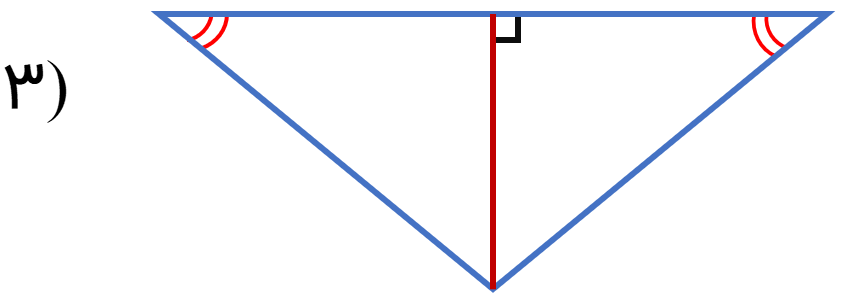
در هر بخش بیان کنید که آیا دو مثلث هم نهشت هستند و دلیل هم نهشتی را بیان کنید (علامت های یکسان، اجزای مساوی را نشان می دهد).
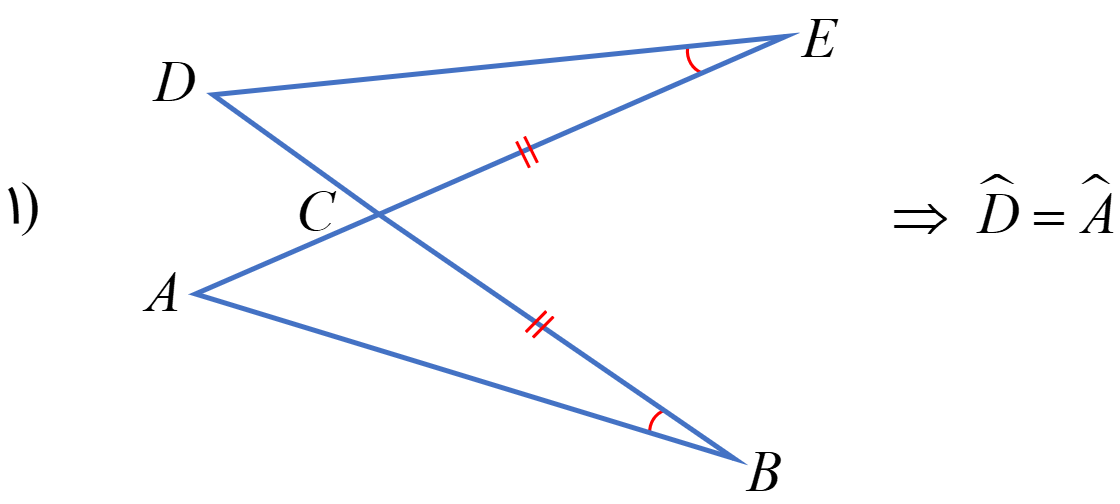
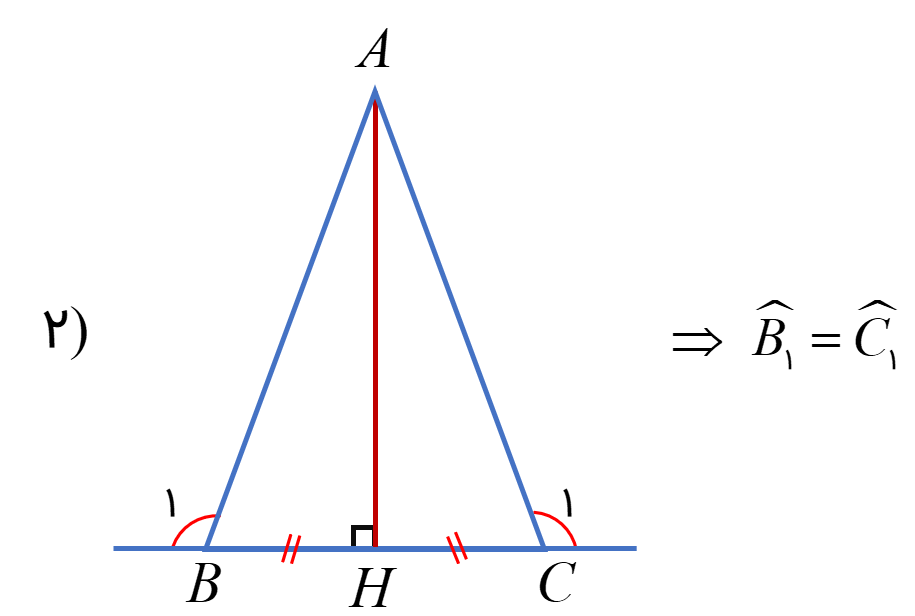
در هر شکل، با توجه به علامت های روی شکل، خواسته سوال را ثابت کنید.
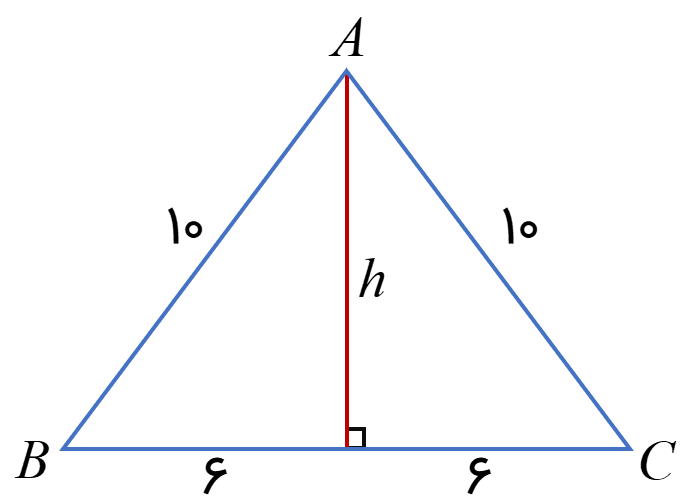
مساحت مثلث متساوی الساقین، 10، 10 و 12 را به دست آورید.
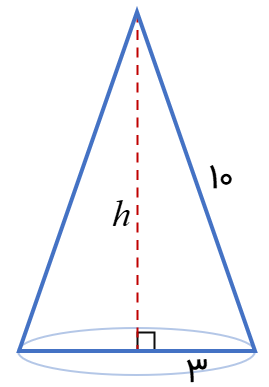
طول ارتفاع مخروط مقابل را به دست آورید.
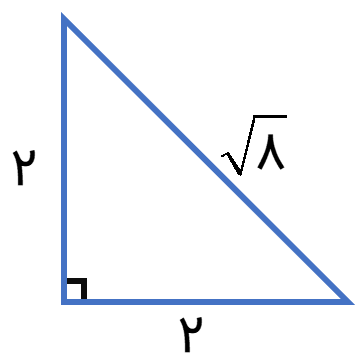
پاره خطی به طول \(\sqrt 8 \) رسم کنید.
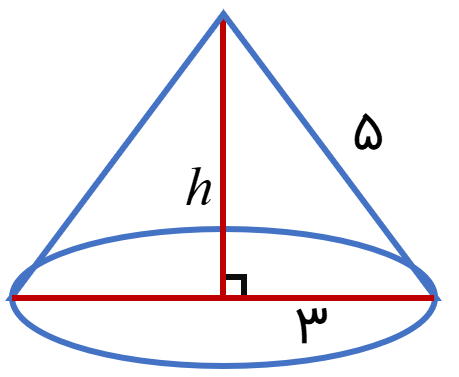
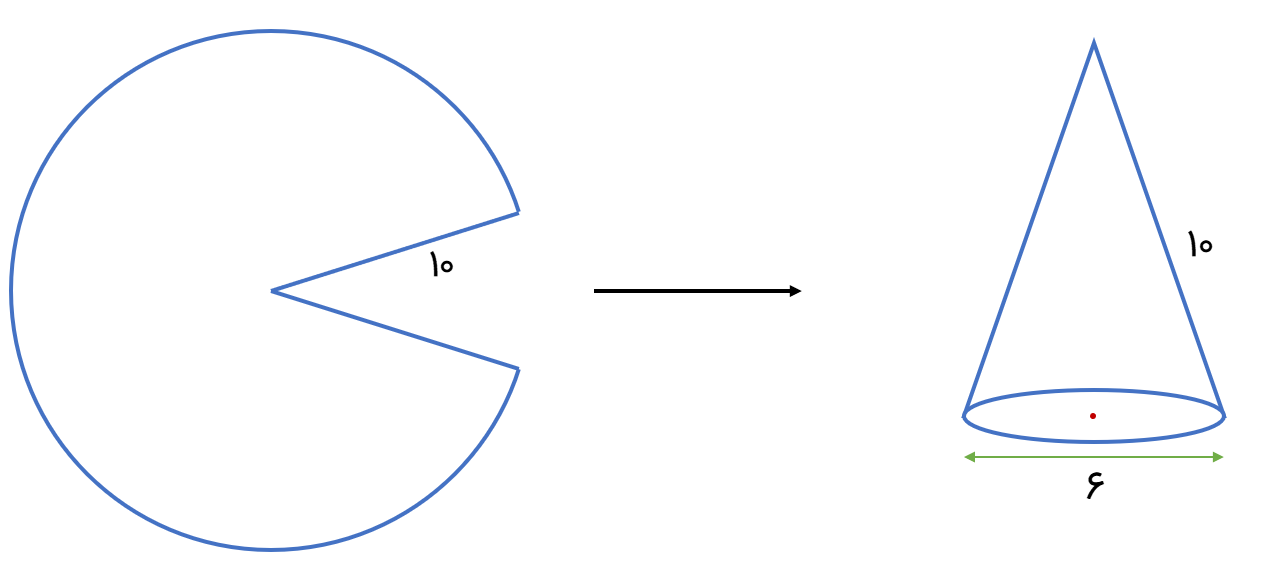
با قسمتی از یک دایره به شعاع 10 سانتی متر به قطر قاعده 6 سانتی متر می سازیم. ارتفاع مخروط را بیابید.
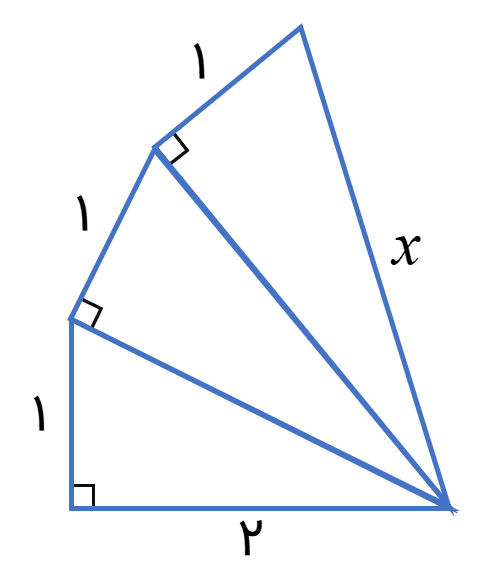
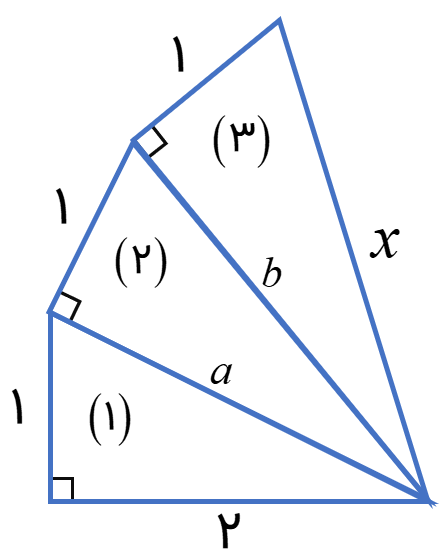
مقدار مجهول x در شکل زیر را به دست آورید.
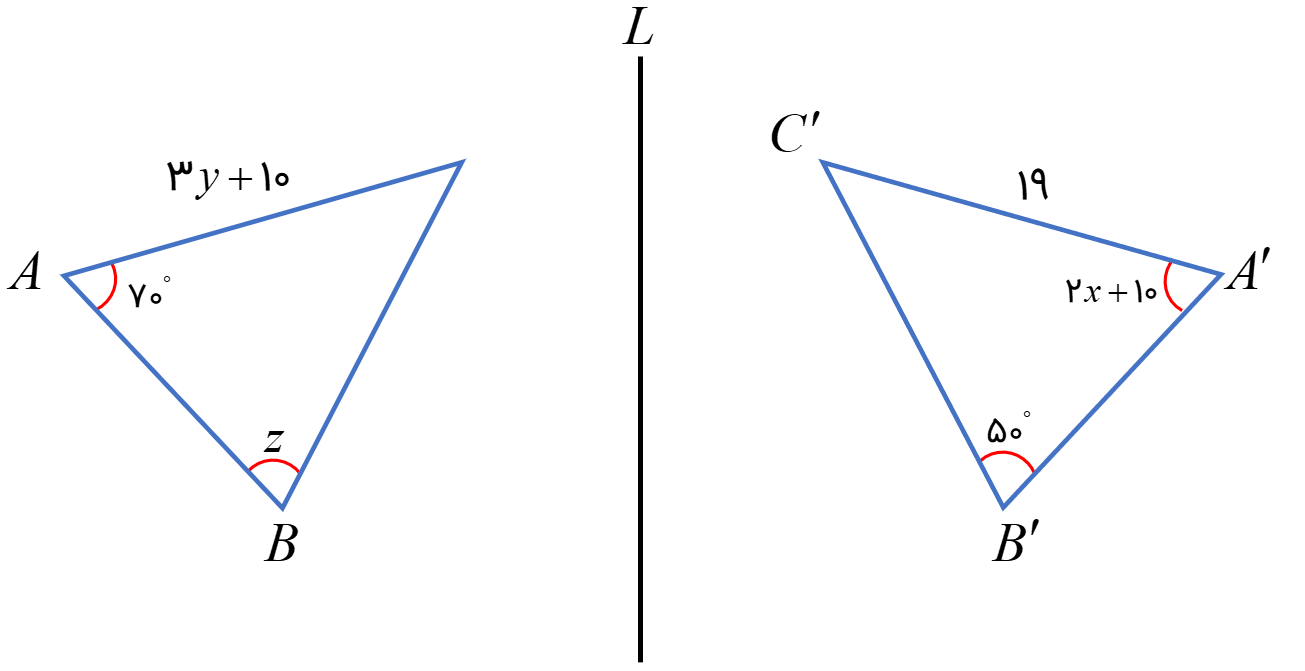
مثلث ABC را نسبت به خط L قرینه می کنیم. مقادیر x، y و z را بیابید.
شکل (2) انتقال یافته شکل (1) است. مقادیر مجهول را بیابید.
«میانه» را تعریف کنید (میانه در مثلث).
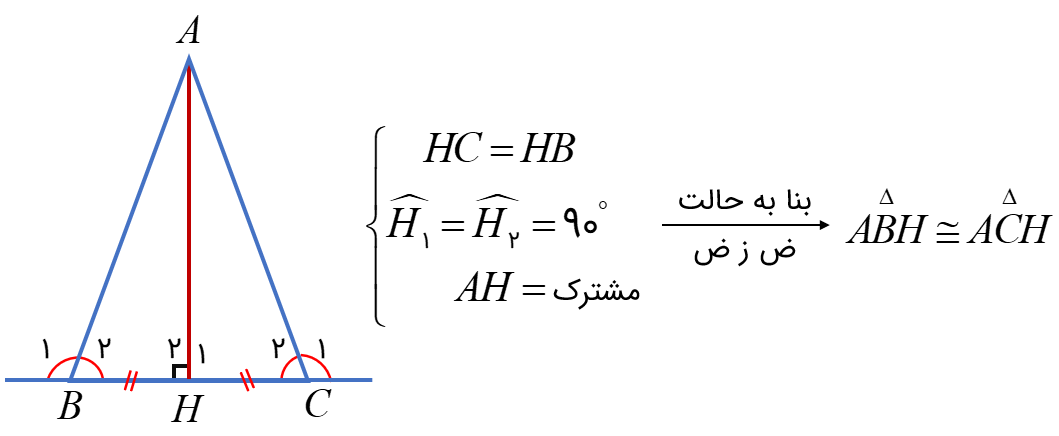
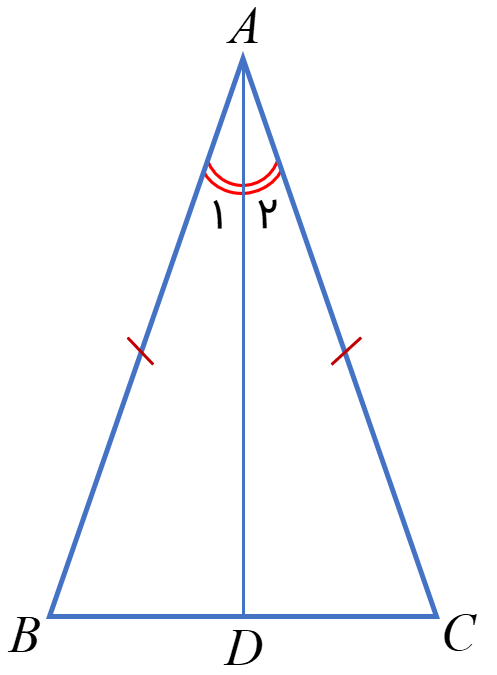
- در مثلث متساوی الساقین ABC \(\left( {AB = AC} \right)\) نیم ساز AD را رسم کرده ایم. ثابت کنید دو مثلث ABD و ACD هم نهشت هستند.
در مثلث ABC، زوایای B و C برابر هستند. نیم ساز AD را رسم می کنیم. ثابت کنید مثلث های \(\mathop {ABD}\limits^\Delta \) و \(\mathop {ACD}\limits^\Delta \) هم نهشت هستند.
در مثلث تند زاویه، همه زاویه های مثلث ..................... هستند.
مثلث متساوی الاضلاع یک مثلث ..................... است.
در مثلث باز گوشه، حتماً یکی از زاویه ها ..................... است.
در مثلث قائم الزاویه، یکی از زاویه ها ..................... است.
در هر مثلث قائم الزاویه، رابطه خاص بین اضلاع برقرار است که به رابطه ..................... معروف است.
رابطه فیثاغورس در هر مثلث قائم الزاویه می گوید که مجموع ..................... اضلاع قائمه، برابر مجذور ..................... است.
اگر در مثلثی رابطه فیثاغورس برقرار باشد، آن مثلث ..................... است.
سه تایی های فیثاغورس، سه عدد ..................... هستند که در رابطه فیثاغورس صدق می کنند.
در هر مثلث قائم الزاویه متساوی الساقین، وتر، ..................... برابر یکی از دو ساق است.
در هر مثلث متساوی الاضلاع، طول ارتفاع، ..................... برابر هر ضلع است.
اگر بتوانیم دو یا چند شکل را با استفاده از تبدیل هندسی (تقارن، انتقال و دوران) بر روی هم قرار دهیم، می گوییم این دو شکل با یکدیگر..................... هستند.
حالت (ض ض ض) در هم نهشتی مثلث ها، یعنی ..................... دو مثلث با یکدیگر برابر هستند.
حالت (ض ز ض) در هم نهشتی مثلث ها، یعنی ..................... متناظر در هر دو مثلث با یکدیگر برابر هستند.
اگر وتر و یک زاویه غیر قائمه از یک مثلث قائم الزاویه با وتر و یک زاویه غیر قائمه از مثلث قائم الزاویه دیگری برابر باشد، آن دو مثلث ..................... هستند.
حالت «وتر و یک ضلع» برابر، برای هم نهشتی بین دو مثلث ..................... کاربرد دارد.
حالت «وتر و یک ضلع» برابر، که در اصل همان حالت ..................... بین دو مثلث می باشد.
رابطه فیثاغورس بین سه عدد 3، 4 و ............ برقرار است.
رابطه فیثاغورس بین سه عدد 5، ............ و 13 برقرار است.
هر نقطه روی ..................... یک زاویه، از دو ضلع آن زاویه، به یک فاصله است.
پاره خطی که از یک رأس مثلث به وسط ضلع روبرو وصل می شود، ..................... نام دارد.



1736019749.png)