گام به گام یادآوری صفحه 21 درس 1 هندسه (1) (ترسیم های هندسی و استدلال)
تعداد بازدید : 51.53Mپاسخ یادآوری صفحه 21 هندسه (1)
-گام به گام یادآوری صفحه 21 درس ترسیم های هندسی و استدلال
-یادآوری صفحه 21 درس 1
-1- در مثلث متساوی الساقین زوایای روبه رو به ساق ها با هم برابرند.
2- اندازۀ هر زاویۀ خارجی یک مثلث برابر است با مجموع اندازه های دو زاویۀ داخلی غیرمجاورش.بنابراین هر زاویۀ خارجی مثلث از هر زاویۀ داخلی غیرمجاورش بزرگ تر است.
می دانیم طبق فرض AB>AC است؛ لذا می توانیم نقطهٔ D را روی AB جایی انتخاب کنیم که AC=AD
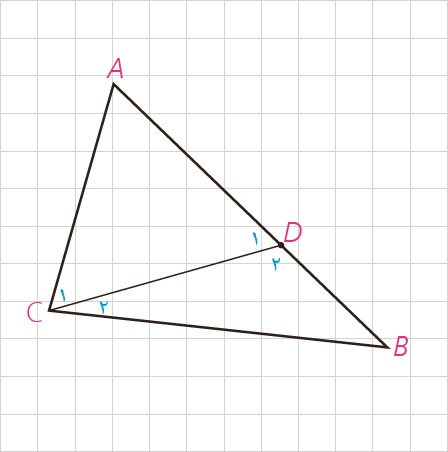
* اندازهٔ زاویه های C و \({C_1}\) نسبت به هم چگونه اند؟ \(\hat C\,\,\, \ldots \,\,\,{\hat C_1}\)
\(\hat C\,\,\, > \,\,\,{\hat C_1}\)
مثلث ADC چه نوع مثلثی است؟
مثلث متساوی الساقین.
** اندازهٔ زاویه های \({C_1}\) و \({D_1}\) نسبت به هم چگونه اند؟ \({\hat C_1}\,\,\, \ldots \,\,\,{\hat D_1}\)
\({\hat C_1}\,\,\, = \,\,\,{\hat D_1}\)
زاویه \({D_1}\) چه نوع زاویه ای برای مثلث DBC است؟
زاویه خارجی
*** اندازهٔ زاویه های \({D_1}\) و B نسبت به هم چگونه اند؟ \({\hat D_1}\,\,\, \ldots \,\,\,\hat B\)
\({\hat D_1}\,\,\, < \,\,\,\hat B\)
از * و ** و *** چه نتیجه ای دربارهٔ اندازهٔ زاویه های B و C می توان گرفت؟
\(\hat C\,\,\, \ldots \,\,\,\hat B\)
\(\hat C\,\,\, > \,\,\,\hat B\)
همان طور که مشاهده کردید در مثلثی مانند \(A\mathop B\limits^\Delta C\) فرض کردیم که ضلع AB>AC است و نشان دادیم: زاویهٔ رو به AC < زاویِۀ رو به رو به AB است.
چرا می توان این موضوع را دربارهٔ تمام مثلث هایی که دو ضلع نابرابر دارند، پذیرفت؟
زیرا این روش اثبات بر اساس اصل ها و قضایایی (واقعیت هایی) است که آن ها را قبول داریم (استدلال استنتاجی)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
