جواب تمرین صفحه 6 درس 1 حسابان یازدهم (جبر و معادله)
تعداد بازدید : 80.73Mپاسخ تمرین صفحه 6 حسابان یازدهم
-گام به گام تمرین صفحه 6 درس جبر و معادله
-تمرین صفحه 6 درس 1
-شما در حال مشاهده جواب تمرین صفحه 6 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 الف به کمک شکل روبه رو حاصل عبارت زیر را به دست آورید.
1+3+5+…+(2n-1)=
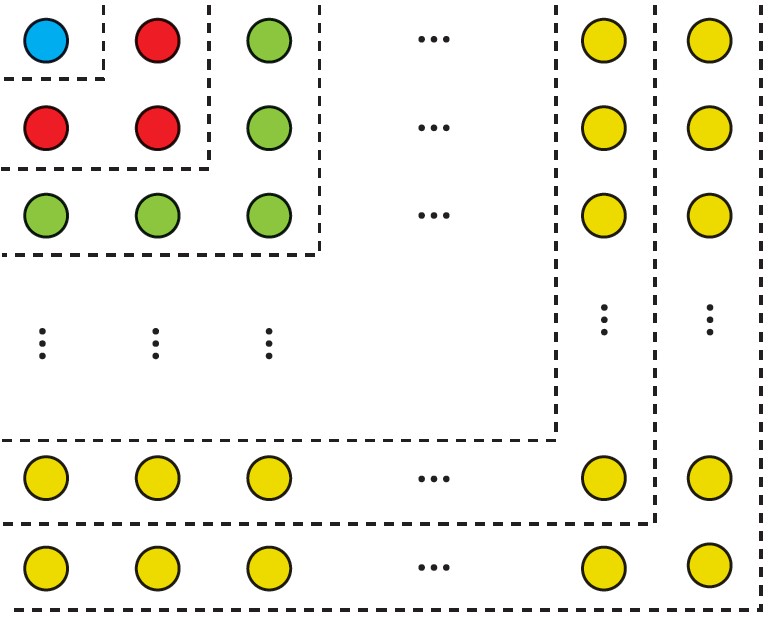
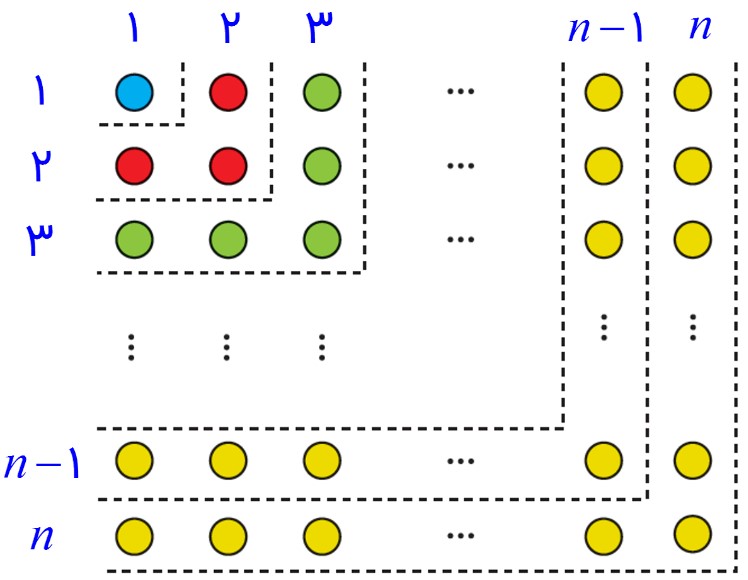
\(1 + 3 + 5 + ... + (2n - 1) = {n^2}\)
ب اکنون با استفاده از فرمول درستی جواب خود در قسمت الف را بررسی کنید.
\(\left. \begin{array}{l}{a_1} = 1\\\\{a_n} = 2n - 1\end{array} \right\} \Rightarrow {S_n} = \frac{n}{2}({a_1} + {a_n}) = \frac{n}{2}(1 + 2n - 1) = {n^2}\)
2 مجموع همه اعداد طبیعی سه رقمی که مضرب شش هستند چقدر می شود؟
\(\begin{array}{l}\left. \begin{array}{l}{a_1} = 102\\\\{a_n} = 996\\\\d = \frac{{{a_n} - {a_{}}}}{{n - 1}}\end{array} \right\} \Rightarrow 6 = \frac{{996 - 102}}{{n - 1}} \Rightarrow n = \frac{{894}}{6} + 1 = 150\\\\ \Rightarrow {S_{150}} = \frac{n}{2}({a_1} + {a_n}) = \frac{{150}}{2}(102 + 996) = 82,350\end{array}\)
3 در دنباله حسابی 5 , 8 , 11 , … حداقل چند جمله آن را با هم جمع کنیم تا حاصل آن از 493 بیشتر شود؟
\(\begin{array}{l}\left. \begin{array}{l}a = 5\\\\d = 3\end{array} \right\} \Rightarrow {a_n} = a + (n - 1)d = 3n + 2\\\\{S_n} > 493 \Rightarrow n = ?\\\\{S_n} = \frac{n}{2}({a_1} + {a_n}) = \frac{n}{2}(3n + 7) > 493\\\\ \Rightarrow 3{n^2} + 7n - 986 > 0 \Rightarrow n > 17 \Rightarrow n = 18\\\\ \Rightarrow {S_{18}} = 594 > 493\end{array}\)
4 در 20 جمله اول یک دنباله حسابی مجموع جملات شماره های فرد 135 و مجموع جملات شماره های زوج 150 می باشد. جمله اول و قدر نسبت دنباله را مشخص کنید.
\(\begin{array}{l}{S_n} = \frac{n}{2}[2a + (n - 1)d]\\\\150 + 135 = \frac{{20}}{2}[2a + 19d] \Rightarrow 20a + 190d = 285\\\\ \Rightarrow 4a + 38d = 57\,\,\,(1)\\\\a + (a + 2d) + (a + 4d) + ... + (a + 18d) = 135\\\\ \Rightarrow 10a + 90d = 135 \Rightarrow 2a + 18d = 27\,\,\,(2)\\\\(1)\,,\,(2):\\\\\left\{ \begin{array}{l}4a + 38d = 57\\\\2a + 18d = 27\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 0\\\\d = 1/5\end{array} \right.\end{array}\)
5 جمله عمومی یک دنباله به صورت \({a_n} = {2^{n - 1}}\) است. چند جمله از این دنباله را با هم جمع کنیم تا مجموع آنها برابر 255 شود؟
\(\begin{array}{l}\left. \begin{array}{l}{a_1} = {2^{ - 1}} = {2^0} = 1\\\\q = 2\\\\{S_n} = 255 \Rightarrow n = ?\end{array} \right\} \Rightarrow {S_n} = {a_1}\frac{{1 - {q^n}}}{{1 - q}}\\\\ \Rightarrow 255 = 1 \times \frac{{1 - {2^n}}}{{1 - 2}} \Rightarrow {2^n} - 1 = 255 \Rightarrow {2^n} = 256 = {2^8}\\\\ \Rightarrow n = 8\end{array}\)
6 طول ضلع مربعی یک متر است. ابتدا نیمی از مساحت مربع را رنگ می کنیم. سپس نیمی از مساحت باقی مانده را و به همین ترتیب در هر مرحله نیمی از مساحت باقی مانده از قبل را رنگ می کنیم. پس از دست کم چند مرحله حداقل 99 درصد سطح مربع رنگ شده است؟
\(\begin{array}{l}\frac{1}{2}\,,\,\frac{1}{4}\,,\,\frac{1}{8}\,,\,...\\\\\left. \begin{array}{l}a = \frac{1}{2}\\\\q = \frac{1}{2}\\\\{S_n} > \frac{{99}}{{100}} \Rightarrow {n_{\min }} = ?\end{array} \right\} \Rightarrow {S_n} = a\frac{{1 - {q^n}}}{{1 - q}} = \frac{1}{2}\frac{{1 - {{(\frac{1}{2})}^n}}}{{1 - \frac{1}{2}}}\\\\ \Rightarrow {S_n} = 1 - {(\frac{1}{2})^n} > \frac{{99}}{{100}} \Rightarrow {(\frac{1}{2})^n} < 1 - \frac{{99}}{{100}} = \frac{1}{{100}}\\\\\left. \begin{array}{l} \Rightarrow \frac{1}{{{2^n}}} < \frac{1}{{100}}\\\\\frac{1}{{{2^7}}} = \frac{1}{{128}} < \frac{1}{{100}}\end{array} \right\} \Rightarrow n = 7\end{array}\)
7 برای عدد حقیقی \((a \ne 1)\,\,a\) و عدد طبیعی n؛
الف حاصل عبارت زیر را به دست آورید.
\(1 + a + {a^2} + ... + {a^{n - 1}}\)
\(\begin{array}{l}1\,,\,a\,,\,{a^2}\,,\,...\,,\,{a^{n - 1}}\\\\{S_n} = 1 + a + {a^2} + ... + {a^{n - 1}}\,\,\,(1)\\\\\left. \begin{array}{l}{a_1} = 1\\\\q = a\end{array} \right\}{S_n} = {a_1}\frac{{1 - {q^n}}}{{1 - q}} = 1 \times \frac{{1 - {a^n}}}{{1 - a}} = \frac{{{a^n} - 1}}{{a - 1}}\,\,\,(2)\\\\(1)\,,\,(2):\\\\1 + a + {a^2} + ... + {a^{n - 1}} = \frac{{{a^n} - 1}}{{a - 1}}\end{array}\)
ب با استفاده از قسمت الف نتیجه بگیرید که:
\({a^n} - 1 = (a - 1)({a^{n - 1}} + ... + {a^2} + a + 1)\)
\(\begin{array}{l}\frac{{{a^n} - 1}}{{a - 1}} = 1 + a + {a^2} + ... + {a^{n - 1}}\\\\{a^n} - 1 = (a - 1)({a^{n - 1}} + ... + {a^2} + a + 1)\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















