جواب تمرین صفحه 15 درس 1 حسابان یازدهم (جبر و معادله)
تعداد بازدید : 80.73Mپاسخ تمرین صفحه 15 حسابان یازدهم
-گام به گام تمرین صفحه 15 درس جبر و معادله
-تمرین صفحه 15 درس 1
-شما در حال مشاهده جواب تمرین صفحه 15 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 معادلهٔ درجه دومی بنویسید که:
الف ریشه های آن \(\frac{1}{2}\) و \(\frac{2}{3}\) باشد.
\(\begin{array}{l}\left\{ \begin{array}{l}\alpha = \frac{1}{3}\\\\\beta = \frac{2}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\alpha + \beta = 1\\\\\alpha \beta = \frac{2}{9}\end{array} \right.\\\\ \Rightarrow {x^2} - (\alpha + \beta )x + \alpha \beta = 0\\\\ \Rightarrow {x^2} - x + \frac{2}{9} = 0\end{array}\)
ب یکی از ریشه های آن دو برابر دیگری باشد (مسئله چند جواب دارد؟).
\(\begin{array}{l}\left\{ \begin{array}{l}\alpha = \alpha \\\\\beta = 2\alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\alpha + \beta = 3\alpha \\\\\alpha \beta = 2{\alpha ^2}\end{array} \right.\\\\ \Rightarrow {x^2} - (\alpha + \beta )x + \alpha \beta = 0\\\\ \Rightarrow {x^2} - 3\alpha x + 2{\alpha ^2} = 0\end{array}\)
مسئله بیشمار جواب دارد.
2 در هر یک از شکل های زیر نمودار سهمی \(P(x) = a{x^2} + bx + c\) داده شده است. در هر حالت صفرهای تابع P(x) و ضابطه آن را مشخص کنید.
الف
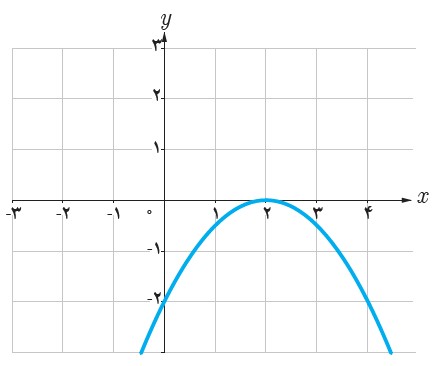
\(\begin{array}{l}\left\{ \begin{array}{l}x = 2 \Rightarrow x - 2 = 0\\\\x = 2 \Rightarrow x - 2 = 0\end{array} \right. \Rightarrow P\left( x \right) = a{\left( {x - 2} \right)^2}\\\\ \Rightarrow P(0) = - 2 \Rightarrow a{(0 - 2)^2} = 4a = - 2\\\\ \Rightarrow a = - \frac{1}{2}\\\\P\left( x \right) = - \frac{1}{2}{\left( {x - 2} \right)^2}\end{array}\)
ب
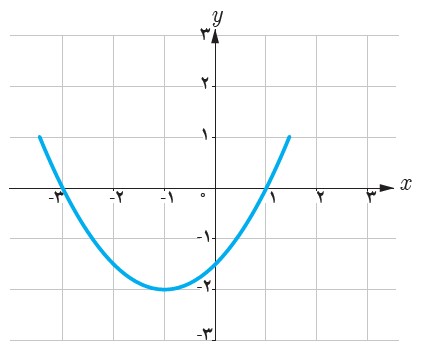
\(\begin{array}{l}\left\{ \begin{array}{l}x = 1 \Rightarrow x - 1 = 0\\\\x = - 3 \Rightarrow x + 3 = 0\end{array} \right. \Rightarrow P(x) = a(x - 1)(x + 3)\\\\ \Rightarrow P( - 1) = - 2 \Rightarrow a( - 1 - 1)( - 1 + 3) = - 4a = - 2\\\\ \Rightarrow a = \frac{1}{2}\\\\ \Rightarrow P(x) = \frac{1}{2}(x - 1)(x + 3)\end{array}\)
3 یک توپ فوتبال بر اثر ضربه بازیکن طبق شکل روبه رو حرکت می کند تا دوباره به زمین بخورد. در هر لحظه ارتفاع توپ از سطح زمین را می توانیم با رابطهٔ \(h(x) = - 0/03x(x - 36)\) مدل سازی کنیم که x فاصله افقی توپ از نقطه اولیه است (x بر حسب متر است)
الف توپ چند متر افقی را طی می کند تا دوباره به زمین بخورد.
\(\begin{array}{l}h(x) = - 0/03x(x - 36) \Rightarrow h(x) = 0\\\\ \Rightarrow \left\{ \begin{array}{l} - 0/03x = 0 \Rightarrow x = 0\\\\x - 36 = 0 \Rightarrow x = 36\end{array} \right.\end{array}\)
ب توپ حداکثر تا چه ارتفاعی بالا می رود.
بیشترین ارتفاع توپ از زمین همان عرض نقطه رأس می باشد؛ بنابراین:
\(\begin{array}{l}{x_ \circ } = \frac{{ - b}}{{2a}} = \frac{{ - \left( { - 0/03 \times 36} \right)}}{{2 \times \left( { - 0/03} \right)}} = 18\\\\ \Rightarrow {y_ \circ } = h\left( {{x_ \circ }} \right) = h\left( {18} \right) = 9/72\end{array}\)
9/72 متر
4 صفرهای توابع زیر را در صورت وجود به دست آورید.
الف\(f(x) = {x^3} - 4x\)
\(\begin{array}{l}f\left( x \right) = {x^3} - 4x = x\left( {{x^2} - 4} \right) = x\left( {x - 2} \right)\left( {x + 2} \right)\\\\ \Rightarrow \left\{ \begin{array}{l}{x_1} = 0\\\\x - 2 = 0 \Rightarrow {x_2} = 2\\\\x + 2 = 0 \Rightarrow {x_3} = - 2\end{array} \right.\end{array}\)
\(g(x) = 2{x^3} + {x^2} + 3x\) ب
\(\begin{array}{l}g(x) = 2{x^3} + {x^2} + 3x = x(2{x^2} + x + 3)\\\\ \Rightarrow \left\{ \begin{array}{l}{x_1} = 0\\\\2{x^2} + x + 3 = 0 \Rightarrow \Delta = {1^2} - 4(2)(3) = - 23 < 0\end{array} \right.\end{array}\)
\(h(x) = {x^4} + 3{x^2} + 5\) پ
\(\begin{array}{l}\left\{ \begin{array}{l}h(x) = {x^4} + 3{x^2} + 5\\\\t = {x^2}\end{array} \right. \Rightarrow {x^4} + 3{x^2} + 5 = {t^2} + 3x + 5\\\\ \Rightarrow \Delta = {3^2} - 4(1)(5) = - 11 < 0\end{array}\)
این تابع، صفر ندارد.
5 معادلات زیر را حل کنید.
\({x^4} - 3{x^2} - 4 = 0\) الف
\(\begin{array}{l}t = {x^2} \Rightarrow {x^4} - 3{x^2} - 4 = 0 \Rightarrow {t^2} - 3t - 4 = 0\\\\ \Rightarrow (t + 1)(t - 4) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}t + 1 = 0 \Rightarrow t = - 1 \Rightarrow {x^2} = - 1 \otimes \\\\t - 4 = 0 \Rightarrow t = 4 \Rightarrow {x^2} = 4 \Rightarrow x = \pm 2\end{array} \right.\\\\ \Rightarrow \left\{ \begin{array}{l}x = - 2\\\\x = 2\end{array} \right.\end{array}\)
\({(\frac{{{x^2}}}{3} - 2)^2} - 7(\frac{{{x^2}}}{3} - 2) + 6 = 0\) ب
\(\begin{array}{l}t = \frac{{{x^2}}}{3} - 2 \Rightarrow {(\frac{{{x^2}}}{3} - 2)^2} - 7(\frac{{{x^2}}}{3} - 2) + 6 = 0\\\\ \Rightarrow {t^2} - 7t + 6 = 0 \Rightarrow (t - 1)(t - 6) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}t - 1 = 0 \Rightarrow t = 1\\\\t - 6 = 0 \Rightarrow t = 6\end{array} \right.\\\\t = 1 \Rightarrow \frac{{{x^2}}}{3} - 2 = 1 \Rightarrow \frac{{{x^2}}}{3} = 3 \Rightarrow {x^2} = 9 \Rightarrow x = \pm 3\\\\t = 6 \Rightarrow \frac{{{x^2}}}{3} - 2 = 6 \Rightarrow \frac{{{x^2}}}{3} = 8 \Rightarrow {x^2} = 24 \Rightarrow x = \pm 2\sqrt 6 \\\\ \Rightarrow \left\{ \begin{array}{l}x = - 3\\\\x = 3\\\\x = - 2\sqrt 6 \\\\x = 2\sqrt 6 \end{array} \right.\end{array}\)
\({(4 - {x^2})^2} - (4 - {x^2}) = 12\) پ
\(\begin{array}{l}t = 4 - {x^2} \Rightarrow {(4 - {x^2})^2} - (4 - {x^2}) = 12\\\\ \Rightarrow {t^2} - t = 12 \Rightarrow {t^2} - t - 12 = 0 \Rightarrow (t - 4)(t + 3) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}t - 4 = 0 \Rightarrow t = 4\\\\t + 3 = 0 \Rightarrow t = - 3\end{array} \right.\\\\t = 4 \Rightarrow 4 - {x^2} = 4 \Rightarrow {x^2} = 0 \Rightarrow x = 0\\\\t = - 3 \Rightarrow 4 - {x^2} = - 3 \Rightarrow {x^2} = 7 \Rightarrow x = \pm \sqrt 7 \\\\ \Rightarrow \left\{ \begin{array}{l}x = 0\\\\x = - \sqrt 7 \\\\x = \sqrt 7 \end{array} \right.\end{array}\)
6 تعداد و مقدار تقریبی ریشه های معادله \(|x - 1| = {x^2} - x - 1\) را با استفاده از روش هندسی به دست آورید.
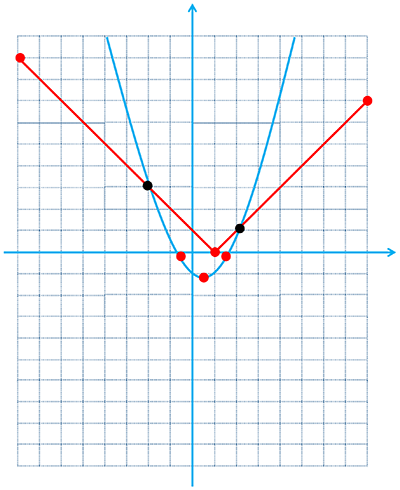
\(\begin{array}{l}|x - 1| = {x^2} - x - 1\\\\ \Rightarrow \left\{ \begin{array}{l}f(x) = |x - 1|\\\\g(x) = {x^2} - x - 1\end{array} \right.\end{array}\)
2 ریشه دارد و این ریشه ها عبارتند از:
\(\left\{ \begin{array}{l}x \simeq - 2\\\\x \simeq 2\end{array} \right.\)
7 هر یک از سهمی های زیر نمودار حالتی از تابع \(f(x) = a{x^2} + bx + c\) است که در آن \(|a| = 1\) است و نقطهٔ رأس سهمی نیز داده شده است.صفرهای تابع را در صورت وجود به دست آورید و ضابطهٔ تابع را مشخص کنید.
الف
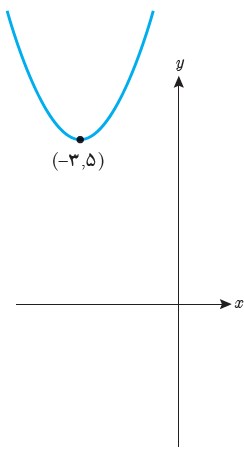
\(\begin{array}{l}a = 1\\\\f\left( x \right) = {x^2} + bx + c\\\\ \Rightarrow {x_0} = \frac{{ - b}}{{2a}} = \frac{{ - b}}{2} = - 3 \Rightarrow b = 6\\\\f\left( { - 3} \right) = 5 = {\left( { - 3} \right)^2} + 6\left( { - 3} \right) + c \Rightarrow c = 14\\\\ \Rightarrow f\left( x \right) = {x^2} + 6x + 14\end{array}\)
ب
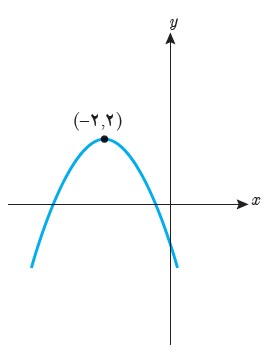
\(\begin{array}{l}a = - 1\\\\g(x) = - {x^2} + bx + c\\\\ \Rightarrow {x_0} = \frac{{ - b}}{{2a}} = \frac{{ - b}}{{ - 2}} = - 2 \Rightarrow b = - 4\\\\g( - 2) = 2 \Rightarrow - {( - 2)^2} - 4( - 2) + c = 2 \Rightarrow c = - 2\\\\g(x) = - {x^2} - 4x - 2\end{array}\)
پ
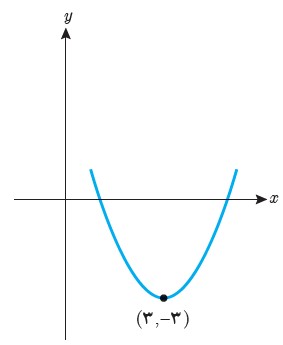
\(\begin{array}{l}a = 1\\\\h\left( x \right) = {x^2} + bx + c\\\\ \Rightarrow {x_0} = \frac{{ - b}}{{2a}} = \frac{{ - b}}{2} = 3 \Rightarrow b = - 6\\\\h(3) = - 3 \Rightarrow {(3)^2} - 6(3) + c = - 3 \Rightarrow c = 6\\\\h\left( x \right) = {x^2} - 6x + 6\end{array}\)
ت
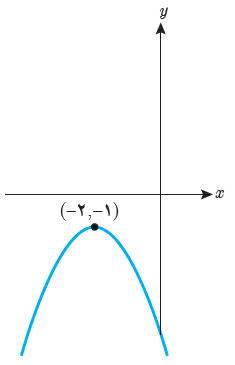
\(\begin{array}{l}a = - 1\\\\i(x) = - {x^2} + bx + c\\\\ \Rightarrow {x_0} = \frac{{ - b}}{{2a}} = \frac{{ - b}}{{ - 2}} = - 2 \Rightarrow b = - 4\\\\i( - 2) = - 1 \Rightarrow - {( - 2)^2} - 4( - 2) + c = - 1 \Rightarrow c = - 5\\\\ \Rightarrow i(x) = - {x^2} - 4x - 5\end{array}\)
8 یک استخر مستطیل شکل به ابعاد طول 10 و عرض 3 متر داریم که یک آبراه بتونی در اطرافش است. اگر این آبراه دارای پهنای یکسان و مساحت 14 متر مربع باشد، پهنای آن را محاسبه است.
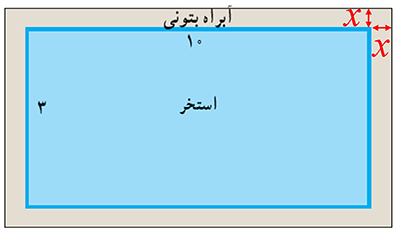
پهنای آبراه = x
\(\begin{array}{l}S = 2 \times x\left( {3 + 2x} \right) + 2 \times x\; \times \;10 = 14\\\\ \Rightarrow 4{x^2} + 26x = 14 \Rightarrow 4{x^2} + 26x - 14 = 0\\\\ \Rightarrow 2{x^2} + 13x - 7 = 0 \Rightarrow \Delta = {(13)^2} - 4(2)( - 7) = 225\\\\ \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 13 \pm 15}}{4} \Rightarrow \left\{ \begin{array}{l}{x_1} = - 7 \otimes \\\\{x_2} = \frac{1}{2}m = 50cm\end{array} \right.\end{array}\)
9 طول یک نوع کاشی یک سانتی متر بلندتر از چهار برابر عرض آن است. برای پوشانیدن دیواری به مساحت 52/8 متر مربع تعداد دو هزار کاشی مصرف شده است. طول هر کاشی چند سانتی متر است؟

طول کاشی = x
عرض کاشی = y
مساحت هر کاشی = S
\(\begin{array}{l}x = 4y + 1\\\\ \Rightarrow S = \frac{{52/8{\;^{{m^2}}}}}{{2000}} \times \frac{{10000{\;^{c{m^2}}}}}{{1{\;^{{m^2}}}}} = 264{\;^{c{m^2}}}\\\\ \Rightarrow S = x \times y = 4{y^2} + y = 264 \Rightarrow 4{y^2} + y - 264 = 0\\\\ \Rightarrow \Delta = {b^2} - 4ac = {(1)^{}} - 4(4)( - 246) = 4225\\\\ \Rightarrow y = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 1 \pm 65}}{8} \Rightarrow \left\{ \begin{array}{l}{y_1} = - \frac{{33}}{4} \otimes \\\\{y_2} = 8\end{array} \right.\\\\y = 8 \Rightarrow x = 4(8) + 1 = 33cm\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















