درسنامه کامل هندسه یازدهم فصل 1 دایره
تعداد بازدید : 7.59Mخلاصه نکات هندسه یازدهم فصل 1 دایره - درسنامه شب امتحان هندسه یازدهم فصل 1 دایره - جزوه شب امتحان هندسه یازدهم نوبت اول فصل 1 دایره
دایره
دایره
دایره پر کاربرد ترین شکل در طبیعت، معماری، صنعت و .... می باشد. به عنوان یک مسئله ریاضی می توان ثابت کرد، در بین تمام شکل های هندسی با محیط ثابت دایره دارای بیشترین مساحت است.
تعریف دایره
مجموعه نقاطی از صفحه که از نقطه ای ثابت O به فاصله ثابت r باشند.
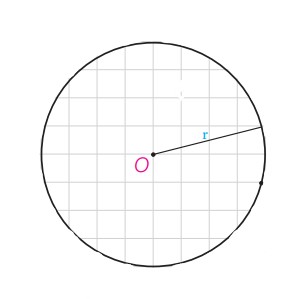
معمولا دایره C به مرکز O و شعاع r را با نماد \(C\left( {O,r} \right)\) نمایش می دهیم.
شعاع دایره
پاره خطی که یک سر آن مرکز دایره و سر دیگر آن نقطه ای روی دایره باشد.

وتر دایره
پاره خطی که دو سر آن روی دایره باشد.
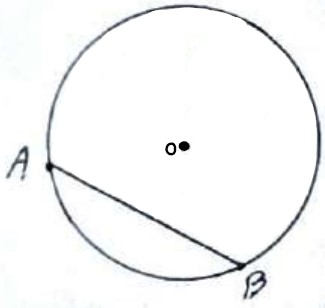
قطر دایره
بزرگترین وتر دایره که از مرکز دایره می گذرد.
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
وضعیت نقطه و دایره
وضعیت نقطه و دایره
هر نقطه نسبت به دایره سه وضعیت داخل، روی و بیرون دایره را دارد. تشخیص این موضوع به فاصله نقطه از مرکز دایره وابسته است.
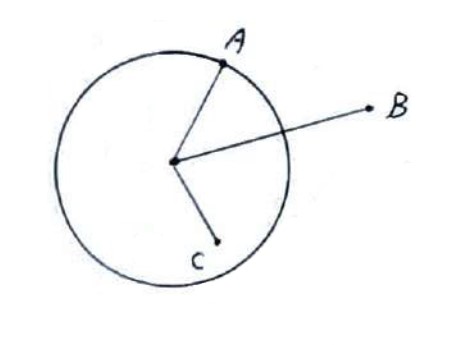
\(\begin{array}{l}OA = r\\\\OB > r\\\\OC < r\end{array}\)
وضعیت نسبی خط و دایره
یک خط با یک دایره سه وضعیت متخارج، مماس و متقاطع را دارد، که از روی فاصله مرکز دایره تا خط قابل تشخیص است.
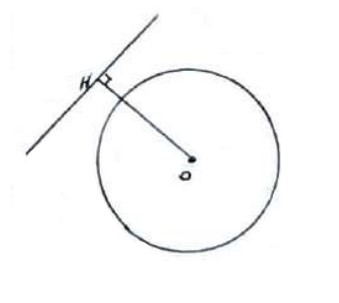
متخارج
\(OH > r\)
خط و دایره نقطه مشترک ندارند.
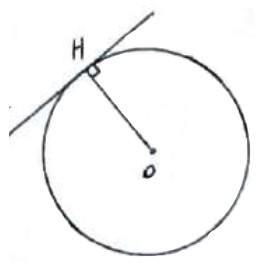
مماس
\(OH = r\)
خط و دایره یک نقطه اشتراک دارند.
متقاطع
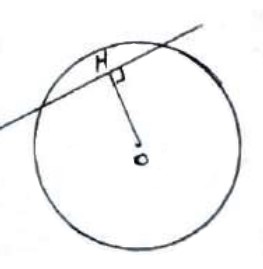
\(OH < r\)
خط و دایره دو نقطه اشتراک دارند.
یک خط بر دایره مماس است، اگر و تنها اگر خط در نقطه تماس بر شعاع دایره عمود باشد.
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
زوایای مرکزی و محاطی
کمان
کمان دایره شامل دو نقطه روی دایره و تمام نقاط بین آن دو نقطه است. (هر کمان قسمتی از محیط دایره است.)
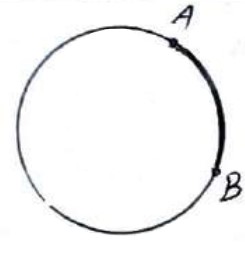
در شکل بالا دو نقطه A و B روی محیط دایره و کمان \(AB\) مشخص شده است.
زاویه مرکزی
زاویه ای که راس آن روی مرکز دایره و ضلع های آن شعاع دایره باشند.
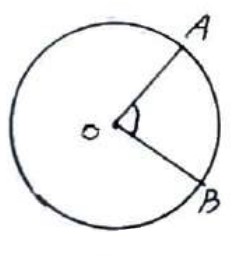
اندازه زاویه مرکزی برابر اندازه کمان مقابلش است:
\(\hat O = \mathop {AB}\limits^\frown \,\)
زاویه محاطی
زاویه ای است که راسش روی محیط دایره و ضلع هایش وتر های دایره باشند.
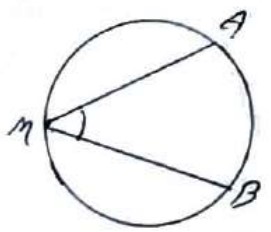
اندازه زاویه محاطی نصف کمان مقابلش است:
\(\hat M = \frac{{\mathop {AB}\limits^\frown }}{2}\)
اندازه کمان
همان اندازه زاویه مرکزی مقابل به آن کمان می باشد و واحد آن درجه است. در دایره های هم مرکز کمان هایی با طول متفاوت؛ دارای اندازه برابر می باشند.
1 رابطه ی بین طول کمان AB و اندازه کمان AB به صورت زیر است:
\(\frac{{\left| {AB} \right|}}{{360}} = \frac{{\mathop {AB}\limits^\frown }}{{2\pi r}}\)
(\(\left| {AB} \right|\) اندازه AB است.)
2 دایره یک کمان است که طول آن \(2\pi r\) و اندازه آن \({360^0}\) می باشد.
در شکل زیر طول و اندازه کمان های AB و CD را بدست آورید.
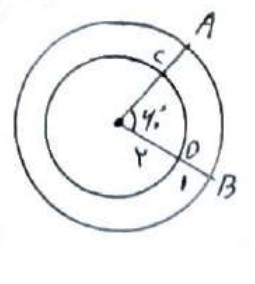
اندازه AB = \({60^0}\)
\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{\left| {AB} \right|}}{{360}} = \frac{{\mathop {AB}\limits^\frown }}{{2\pi r}} \Rightarrow \frac{{60}}{{360}} = \frac{{\mathop {AB}\limits^\frown }}{{2\pi 3}}\\\end{array}\\{ \Rightarrow \mathop {AB}\limits^\frown = \frac{1}{6} \times 6\pi = \pi }\end{array}\)
اندازه CD = \({60^0}\)
\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{\left| {CD} \right|}}{{360}} = \frac{{\mathop {CD}\limits^\frown }}{{2\pi r}} \Rightarrow \frac{{60}}{{360}} = \frac{{\mathop {CD}\limits^\frown }}{{2\pi 2}}\\\end{array}\\{ \Rightarrow \mathop {CD}\limits^\frown = \frac{1}{6} \times 4\pi = \frac{{2\pi }}{3}}\end{array}\)
تهیه کننده: امیرحسین مطلبی
قطاع
قطاع
ناحیه ای از درون و روی دایره را، که به دو شعاع دایره و آن دایره محدود است یک قطاع دایره می نامند.
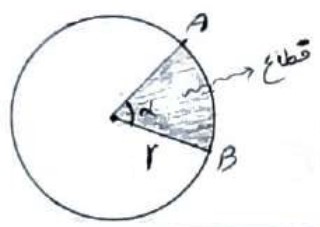
طول کمان نظیر قطاع
اگر طول کمان AB نظیر قطاع را L در نظر بگیریم از رابطه زیر حاصل می شود:
\(L = \frac{{2\pi r}}{{360}}\alpha \)
اثبات
\(\begin{array}{l}\frac{{\left| {AB} \right|}}{{360}} = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{{2\pi r}} \Rightarrow \frac{\alpha }{{360}} = \frac{L}{{2\pi r}}\\\\ \Rightarrow L = \frac{{2\pi r}}{{360}}\alpha \end{array}\)
مساحت قطاع
اگر مساحت قطاع که زاویه مرکزی آن \(\alpha \) می باشد را S در نظر بگیریم:
\(S = \frac{{\pi {r^2}}}{{360}}\alpha \)
اثبات:
می دانیم یک درجه، \(\frac{1}{{360}}\) دایره است، پس مساحت قطاعی که زاویه مرکزی آن 1 درجه است؛ \(\frac{1}{{360}}\) مساحت دایره است؛ در نتیجه مساحت قطاعی که زاویه مرکزی آن \(\alpha \) درجه است، \(\frac{\alpha }{{360}}\) مساحت دایره است.
مساحت قطاع = \(\frac{\alpha }{{360}} \Rightarrow S = \frac{\alpha }{{360}} = \pi {r^2} \Rightarrow S = \frac{{\pi {r^2}}}{{360}}\alpha \)
1 طول کمان های AB و CD و مساحت قسمت هاشور خورده را بدست آورید.
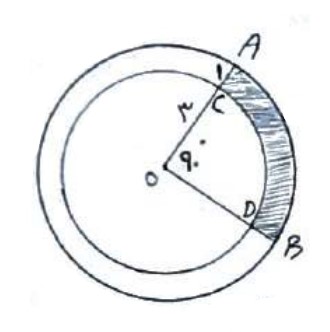
طول کمان AB = \(\frac{{2\pi r}}{{360}}\alpha = \frac{{2\pi 4}}{{360}} \times 90 = 2\pi \)
طول کمان CD = \(\frac{{2\pi r}}{{360}}\alpha = \frac{{2\pi \times 3}}{{360}} \times 90 = \frac{{3\pi }}{2}\)
مساحت قسمت هاشور خورده: \({S_{A\mathop O\limits^\Delta B}} - {S_{C\mathop O\limits^\Delta D}} = \)
\(\begin{array}{l}\frac{{\pi \times {4^2}}}{{360}} \times 90 - \frac{{\pi \times {3^2}}}{{360}} \times 90 = \\\\\frac{{16\pi }}{4} - \frac{{9\pi }}{4} = \frac{{7\pi }}{4}\end{array}\)
2 در شکل زیر اگر O مرکز دایره و مساحت ناحیه هاشور خورده برابر 18 باشد، طول کمان AB را بدست آورید. (\(\pi = 3\))
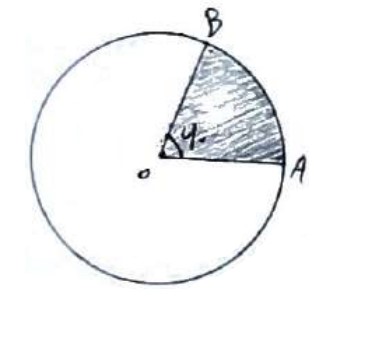
\(\begin{array}{l}{S_{A\mathop O\limits^\Delta B}} = 18 \Rightarrow \frac{{\pi {r^2}}}{{360}} \times 60 = 18\\\\ \Rightarrow \frac{{3{r^2}}}{6} = 18 \Rightarrow {r^2} = 36 \Rightarrow r = 6\end{array}\)
طول کمان AB = \(\frac{{2\pi r}}{{360}}\alpha = \frac{{2\pi 6}}{{360}} \times 60 = \)
\(2\pi = 2 \times 3 = 6\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
وتر و کمان نظیر آن
وتر و کمان نظیر آن
در شکل زیر کمان AB نظیر و وتر AB می باشد.
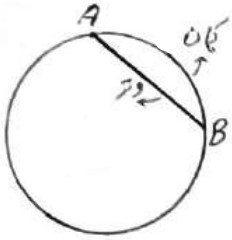
مثال
ثابت کنید در هر دایره کمان های نظیر دو وتر مساوی باهم برابرند و برعکس.
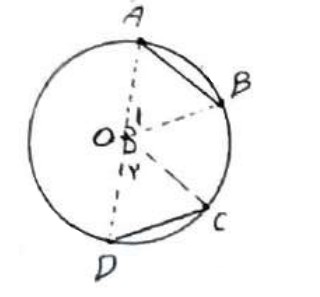
فرض: \(AB = CD\) برابری دو وتر
حکم: \(\mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown {\mkern 1mu} \) برابری دو کمان
\(\begin{array}{*{20}{l}}{AB = CD}\\{}\\{OA = OD}\\{}\\{OB = OC}\\{}\\\begin{array}{l} \Rightarrow O\mathop {{\rm{ }}A}\limits^\Delta B \cong O\mathop {{\rm{ }}D}\limits^\Delta C \Rightarrow {{\hat O}_1} = {{\hat O}_2}\\\\ \Rightarrow \mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown \end{array}\end{array}\)
حال عکس این فرض را اثبات می کنیم:
فرض: \(\mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown \) برابری دو کمان
حکم: \(AB = CD\) برابری دو وتر
\(\begin{array}{*{20}{l}}{\mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown \Rightarrow {{\hat O}_1} = {{\hat O}_2}}\\{}\\{OA = OD}\\{}\\{OB = OC}\\{}\\{ \Rightarrow O\mathop {{\rm{ }}A}\limits^\Delta B \cong O\mathop {{\rm{ }}C}\limits^\Delta D \Rightarrow AB = CD}\end{array}\)
قضیه 1
در هر دایره، قطر عمود بر وتر، آن وتر و کمان نظیر آن وتر را نصف می کند.
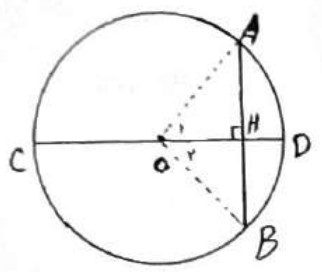
فرض: \(CD \bot AB\)
حکم: \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}AH = BH\\\end{array}\\{\mathop {{\rm{AD}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{BD}}}\limits^\frown }\end{array}} \right.\)
\(\begin{array}{*{20}{l}}{OA = OB}\\{}\\{OH = OH}\\{}\\\begin{array}{l} \Rightarrow O\mathop {{\rm{ }}A}\limits^\Delta H \cong O\mathop {{\rm{ }}B}\limits^\Delta H \Rightarrow {{\hat O}_1} = {{\hat O}_2}\\\\ \Rightarrow \mathop {{\rm{AD}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{BD}}}\limits^\frown \end{array}\end{array}\)
عکس قضیه 1
اگر قطری از دایره، وتر و کمان نظیر آن وتر را نصف کند، آنگاه قطر بر وتر عمود است.
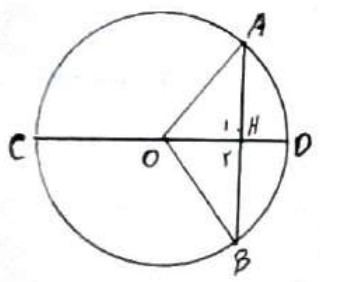
فرض: \({\rm{AH = BH}}\,\,\,{\rm{,}}\,\,\,\mathop {{\rm{AD}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{BD}}}\limits^\frown \)
حکم: \(CD \bot AB\)
\(\begin{array}{l}AH = BH\\\\OH = OH\\\\OA = OB\\\\ \Rightarrow O\mathop A\limits^\Delta H \cong O\mathop B\limits^\Delta H \Rightarrow {H_1} = {H_2}\\\\ \Rightarrow {{\hat H}_1} = {{\hat H}_2} \Rightarrow CD \bot AB\end{array}\)
قضیه 2
اندازه هر زاویه محاطی برابر است با نصف اندازه کمان مقابل به آن زاویه.
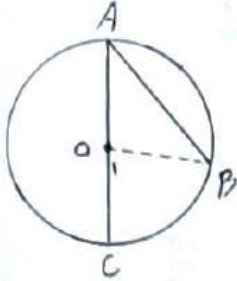
فرض: زاویه محاطی \(\hat A\)
حکم: \(\hat A = \frac{{\mathop {BC}\limits^\frown {\mkern 1mu} }}{2}\)
اثبات:
با وصل کردن B به O داریم:
\(\begin{array}{*{20}{l}}{{{\hat O}_1} = \hat A + \hat B}\\{}\\{O\mathop {{\rm{ }}A}\limits^\Delta B:\hat A = \hat B}\\{}\\{ \Rightarrow {{\hat O}_1} = 2\hat A \Rightarrow \hat A = \frac{{{{\hat O}_1}}}{2} \Rightarrow {{\hat O}_1} = \mathop {BC}\limits^\frown {\mkern 1mu} }\\{}\\{ \Rightarrow \hat A = \frac{{\mathop {BC}\limits^\frown {\mkern 1mu} }}{2}}\end{array}\)
1 در قضیه بالا یکی از اضلاع زاویه محاطی قطر دایره بود. اما می توان حالت های دیگری را برای قضیه بالا در نظر گرفت، مثلا دو ضلع زاویه محاطی دو طرف مرکز دایره باشند، یا دو ضلع زاویه محاطی در یک طرف مرکز باشند.
2 زاویه محاطی زیر به قطر دایره، \({90^0}\) (قائمه) است.
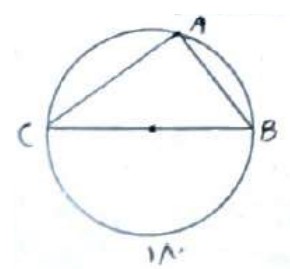
محاطی مقابل قطر \(\hat A = \frac{{\mathop {BC}\limits^\frown {\mkern 1mu} }}{2} = \frac{{{{180}^ \circ }}}{2} = {90^ \circ }\)
1 دایره \(C\left( {O,36} \right)\) و وتر AB به فاصله 10 از مرکز دایره مفروضند. طول وتر AB را بدست آورید.
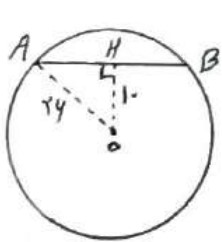
رابطه فیثاغورث: \(O{A^2} = A{H^2} + O{H^2}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{26}^2} = A{H^2} + {{10}^2}}\\{}\\\begin{array}{l} \Rightarrow A{H^2} = {26^2} - {10^2}\\\\ \Rightarrow A{H^2} = 576\end{array}\\{}\\{ \Rightarrow AH = 24}\end{array}\)
می دانیم قطر عمود بر وتر، وتر را نصف می کند پس، \(AH = BH = 24\) و در نتیجه:
\(AB = 2 \times 24 = 48\)
2 در شکل زیر اندازه زاویه های X و Y را بدست آورید.
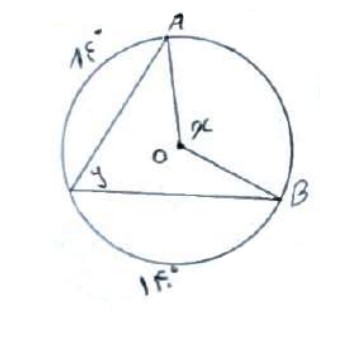
\(AB + {140^0} + {84^0} = {360^0} \Rightarrow AB = {136^0}\)
زاویه مرکزی \(\hat X = AB = {136^0}\)
زاویه محاطی \(\hat Y = \frac{{AB}}{2} = \frac{{136}}{2} = {68^0}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
زاویه ظلی
زاویه ظلی
زاویه ای است که راس آن روی دایره قرار دارد و یک ضلع آن مماس بر دایره و ضلع دیگر آن (قاطع دایره) وتر دایره می باشد.
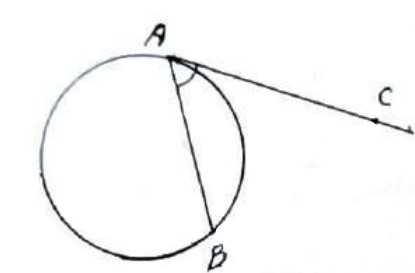
در شکل بالا زاویه \(B\hat AC\) ظلی است.
قضیه
اندازه هر زاویه ظلی برابر نصف کمان رو به روی آن است.
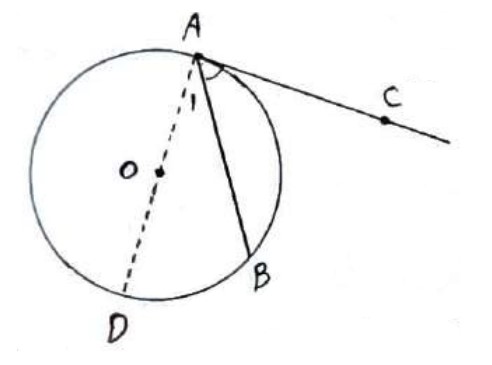
فرض: ظلی \(\hat A\)
حکم: \(\hat A = \frac{{AB}}{2}\hat A = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{2}\)
قطر گذرنده از A را رسم می کنیم تا دایره را در D قطع کند.
\(\begin{array}{*{20}{l}}{D\hat AC = {{90}^0} \Rightarrow D\hat AC = \frac{{\mathop {AD}\limits^\frown {\mkern 1mu} }}{2}}\\{}\\{{{\hat A}_1} = \frac{{\mathop {BD}\limits^\frown {\mkern 1mu} }}{2}}\\{}\\\begin{array}{l} \Rightarrow D\hat AC - {{\hat A}_1} = \frac{{\mathop {AD}\limits^\frown {\mkern 1mu} - \mathop {BD}\limits^\frown {\mkern 1mu} }}{2}\\\\ \Rightarrow \hat A = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{2}\end{array}\end{array}\)
1 با توجه به شکل مقابل اندازه زاویه ظلی \(\alpha \) را بدست آورید.
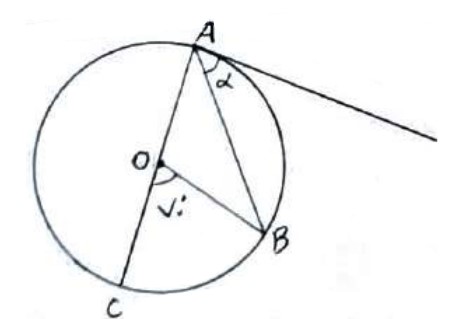
مرکزی: \(C\hat OB = {70^0} \Rightarrow BC = {70^0}\)
قطر است \({AC \Rightarrow \mathop {AB}\limits^\frown = {{180}^ \circ } - {{70}^ \circ } = {{110}^ \circ }}\)
\({\alpha = \frac{{AB}}{2} = \frac{{{{110}^ \circ }}}{2} = {{55}^ \circ }}\)
2 در شکل زیر AT بر دایره در نقطه A مماس است، با توجه به شکل زیر مقدار X و Y را بدست آورید.
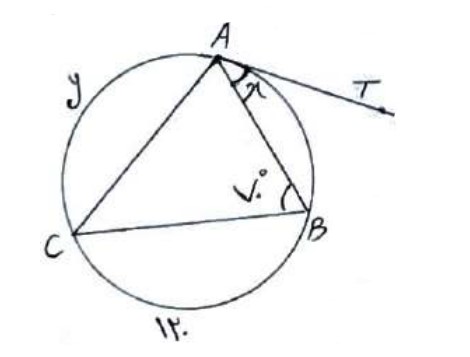
محاطی \(\hat B = \frac{{\mathop {AC}\limits^\frown {\mkern 1mu} }}{2} \Rightarrow \mathop {AC}\limits^\frown = 2 \times {70^ \circ } \Rightarrow \hat Y = {140^ \circ }\)
\(\begin{array}{*{20}{l}}{\mathop {AB}\limits^\frown = {{360}^ \circ } - \left( {{{120}^ \circ } + {{140}^ \circ }} \right) = {{100}^ \circ }}\\{}\\{\hat X = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{2} = \frac{{{{100}^ \circ }}}{2} = {{50}^ \circ }}\end{array}\)
تهیه کننده: امیرحسین مطلبی
زاویه بین وتر های متقاطع
زاویه بین وتر های متقاطع
الف)
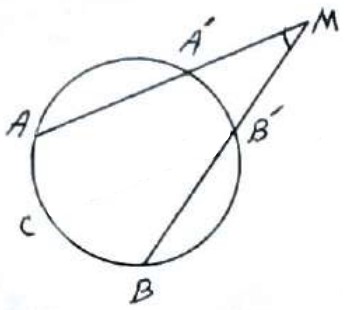
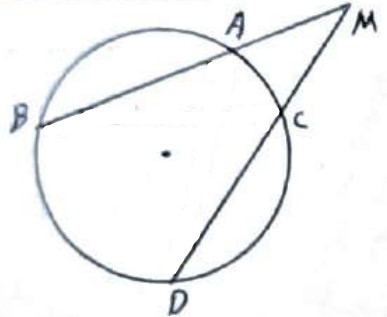
اگر دو وتر در خارج دایره متقاطع باشند، زاویه بین آنها برابر است با نصف تفاضل دو کمان مقابل به آن زاویه:
\(\hat M = \frac{{AB - A'B'}}{2}\)
اثبات (روش اول)
از \(B'\) خطی موازی \(AA'\) رسم می کنیم تا دایره را در C قطع کند.
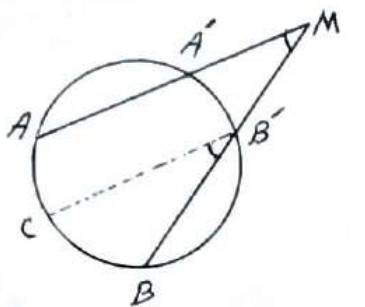
\(\begin{array}{l}AA'\parallel CB' \Rightarrow \hat M = \hat B' = \frac{{BC}}{2}\\\\ \Rightarrow \frac{{AB - AC}}{2} = \frac{{AB - A'B'}}{2}\end{array}\)
اثبات (روش دوم)
از \(B'\) به A وصل می کنیم، زاویه \(B'\) زاویه خارجی مثلث \(A\mathop M\limits^\Delta B\) است.
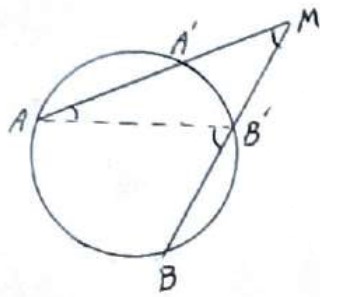
\(\begin{array}{l}\hat B' = \hat A = \hat M \Rightarrow \hat M = \hat B' - \hat A\\\\ \Rightarrow \frac{{AB}}{2} - \frac{{A'B'}}{2} \Rightarrow \frac{{AB - A'B'}}{2}\end{array}\)
ب) اگر دو وتر در داخل دایره متقاطع باشند، زاویه بین آنها برابر است با نصف مجموع دو کمان مقابل به آن زاویه.
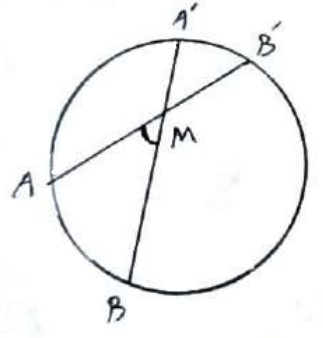
\(\hat M = \frac{{AB + A'B'}}{2}\)
اثبات
از A به \(\hat A\) وصل کنیم، زاویه مشخص شده M زاویه خارجی برای مثلث \(A\mathop {A'}\limits^\Delta M\) می باشد.
خارجی \(\begin{array}{l}\hat M = \hat A + \hat A' = \frac{{A'B'}}{2} + \frac{{AB}}{2}\\\\ \Rightarrow \hat M = \frac{{AB + A'B'}}{2}\end{array}\)
1 با توجه به شکل زیر مقدار های X و Y را تعیین کنید.
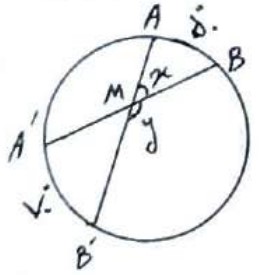
\(\begin{array}{l}\hat X = \frac{{50 + 70}}{2} = \frac{{120}}{2} = {60^0}\\\\\hat Y = 180 - X = 180 - 60 = {120^0}\end{array}\)
2 اندازه زاویه \(\alpha \) را در شکل زیر بیابید.
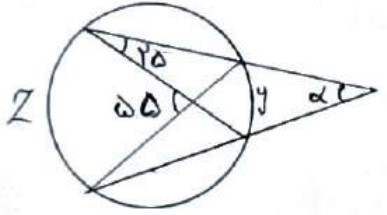
\(\begin{array}{l}25 = \frac{Y}{2} \Rightarrow Y = 2 \times 25 = 50\\\\55 = \frac{{Z + Y}}{2} \Rightarrow 110 = Z + 50 \Rightarrow Z = 60\\\\\alpha = \frac{{Z - Y}}{2} = \frac{{60 - 50}}{2} = \frac{{10}}{2} = 5\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
رابطه های طولی در دایره
رابطه های طولی در دایره
اگر وتر های یک دایره یکدیگر را درون دایره قطع کنند یا امتداد وتر ها یکدیگر را در خارج دایره قطع کنند بین اندازه پاره خط های ایجاد شده روابطی برقرار است که در قضیه های زیر به آنها می پردازیم.
قضیه 1
هر گاه دو وتر دلخواه AB و CD یکدیگر را درون دایره در نقطه M قطع کنند، آنگاه:
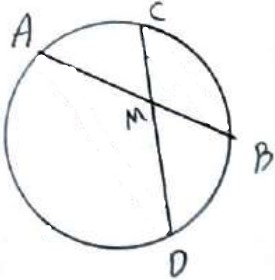
\(MA \times MB = MC \times MD\)
اثبات
از A به D و از B به C وصل می کنیم در دو مثلث ایجاد شده داریم:
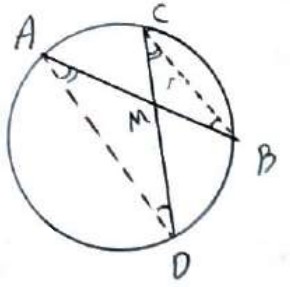
محاطی \(\hat A = \hat C = \frac{{BD}}{2}\)
محاطی \(\hat B = \hat D = \frac{{AC}}{2}\)
\(\begin{array}{l} \Rightarrow A\mathop M\limits^\Delta D \sim B\mathop M\limits^\Delta C \Rightarrow \frac{{AM}}{{MC}} = \frac{{MD}}{{MB}}\\\\ \Rightarrow AM \times MB = MC \times MD\end{array}\)
مثال
در شکل زیر مقدار X را بدست آورید.
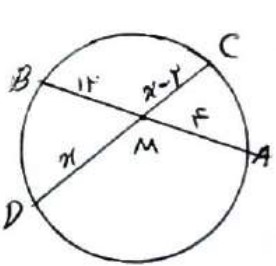
طبق روابط طولی: \(MA \times MB = MC \times MD\)
\(\begin{array}{l}4 \times 12 = \left( {x - 2} \right)x \Rightarrow 48 = {x^2} - 2x\\\\ \Rightarrow {x^2} - 2x - 48 = 0\\\\ \Rightarrow \left( {x - 8} \right)\left( {x + 6} \right) = 0 \Rightarrow x = 8\;,\;x = - 6\end{array}\)
قضیه 2
هرگاه امتداد های دو وتر AB و CD یکدیگر را خارج دایره در نقطه M قطع کنند آنگاه:
\(MA \times MB = MC \times MD\)
اثبات
از A به D و از C به B وصل می کنیم، در مثلث ایجاد شده داریم:
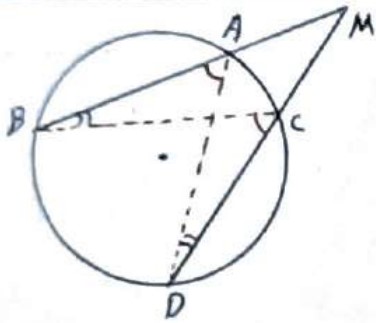
\(\begin{array}{l}\hat B = \hat D = \frac{{AC}}{2}\\\\\hat M = \hat M\\\\A\mathop M\limits^\Delta D \sim C\mathop M\limits^\Delta B \Rightarrow \frac{{MA}}{{MC}} = \frac{{MD}}{{MB}}\\\\ \Rightarrow MA \times MB = MC \times MD\end{array}\)
مثال
در شکل زیر مقدار X را بدست آورید.
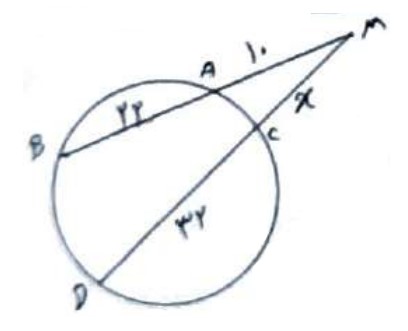
طبق روابط طولی: \(MA \times MB = MC \times MD\)
\(\begin{array}{l} \Rightarrow 10 \times 32 = x \times \left( {x + 32} \right)\\\\ \Rightarrow {x^2} + 32x - 320 = 0\\\\ \Rightarrow \left( {x + 40} \right)\left( {x - 8} \right) = 0\\\\ \Rightarrow x = - 40\;,\;x = 8\end{array}\)
که در اینجا \(x = 8\) قابل قبول است.
قضیه 3
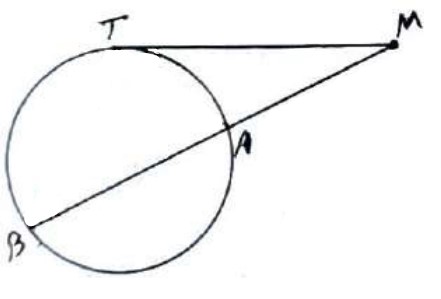
هرگاه از نقطه M خارج دایره یک مماس و یک قاطع بر دایره رسم کنیم، آنگاه مربع اندازه مماس برابر است با حاصل ضرب اندازه های دو قطعه قاطع، یعنی:
\(M{T^2} = MA \times MB\)
(به عبارت دیگر طول مماس واسطه هندسی بین دو قطعه قاطع است.)
اثبات
از T به A و B وصل می کنیم در دو مثلث \(M\mathop A\limits^\Delta T\) و \(M\mathop B\limits^\Delta T\) داریم:
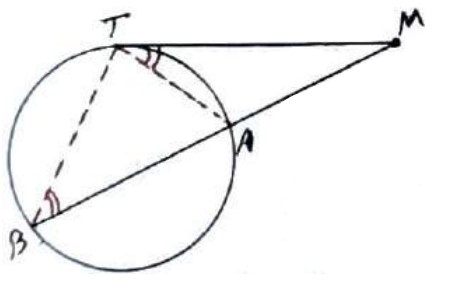
\(\begin{array}{l}\hat B = \hat T = \frac{{AT}}{2}\\\\\hat M = \hat M\\\\ \Rightarrow M\mathop A\limits^\Delta T \sim M\mathop B\limits^\Delta T \Rightarrow \frac{{MA}}{{MT}} = \frac{{MT}}{{MB}}\\\\M{T^2} = MA \times MB\end{array}\)
در شکل زیر مقادیر مجهول را بدست آورید.
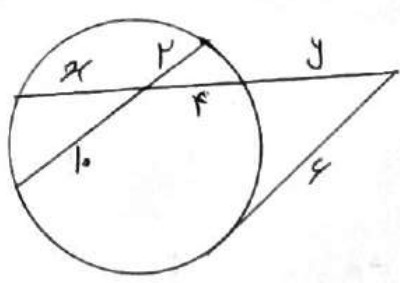
روابط طولی: \(4 \times x = 2 \times 10 \Rightarrow x = \frac{{20}}{4} = 5\)
\(\begin{array}{l}{6^2} = y\left( {y + 9} \right) \Rightarrow 36 = {y^2} + 9y\\\\ \Rightarrow {y^2} + 9y - 36 = 0\\\\ \Rightarrow \left( {y + 12} \right)\left( {y - 3} \right) = 0\\\\ \Rightarrow y = - 12\;,\;y = 3\end{array}\)
که در اینجا \(y = 3\) قابل قبول و جواب است.
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
رسم مماس بر دایره از نقطه ای خارج دایره
رسم مماس بر دایره از نقطه ای خارج دایره
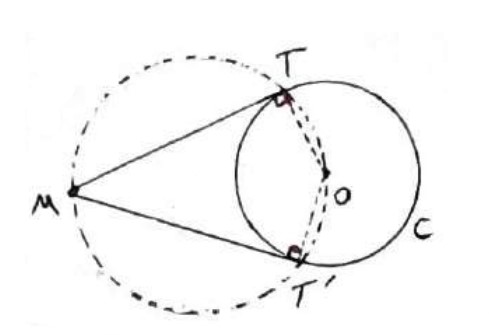
نقطه دلخواه M خارج دایره \(C\left( {O,R} \right)\) را در نظر می گیریم؛ حال دایره ای به قطر OM رسم می کنیم، به طوری که دایره \(C\left( {O,R} \right)\) را در نقاط T و \(T'\) قطع کند، در این صورت خط های MT و \(MT'\) بر دایره \(C\left( {O,R} \right)\) مماس هستند.
زیرا اگر از T و \(T'\) به O وصل کنیم، زاویه های T و \(T'\) محاطی رو به رو به قطر می باشند، پس \({90^0}\) می باشند؛ لذا چون MT و \(MT'\) بر شعاع در نقطه T و \(T'\) عمودند، پس MT و \(MT'\) مماس بر دایره می باشند.
در شکل زیر \(BC = 10\) ، \(AC = 8\) و \(AB = 12\) طول \(x = BF\) چند واحد است؟
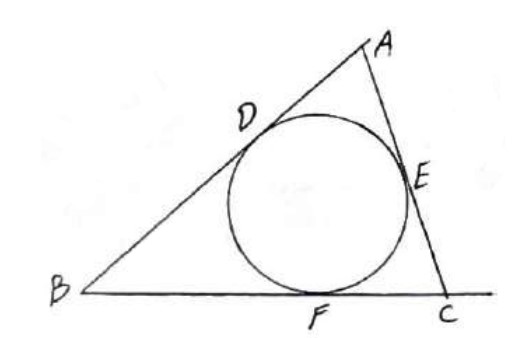
می دانیم طول 2 مماس رسم شده بر دایره از نقطه خارج دایره باهم برابر است.
\(\begin{array}{l}AD = AE\\\\BD = BF\\\\CF = CE\\\\ \Rightarrow AD + BD + CF = AE + BF + CE\\\\ \Rightarrow \left( {CF = BC - BF\;,\;AE + CE = AC} \right)\\\\ \Rightarrow AD + BC - BF = AC + BF\\\\ \Rightarrow 12 + 10 - x = 8 + x\\\\ \Rightarrow 2x = 14 \Rightarrow x = 7\end{array}\)
تهیه کننده: امیرحسین مطلبی
حالت های دو دایره نسبت به هم
حالت های دو دایره نسبت به هم
پاره خطی که مرکز های دو دایره را به هم وصل می کند را خط المرکزین گویند و با d نشان می دهند.
دو دایره \(C\left( {O,R} \right)\) و \(C'\left( {O',R'} \right)\) را بر فرض \(R\rangle R'\) و \(OO' = d\) در نظر می گیریم. حالت های مختلفی که این دو دایره می توانند نسبت به هم داشته باشند به صورت زیر است:
دو دایره برون هم (متخارج)
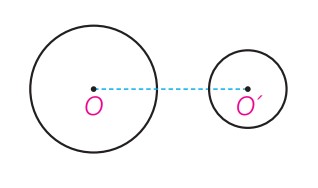
\(d\rangle R + R'\)
دو دایره مماس برون
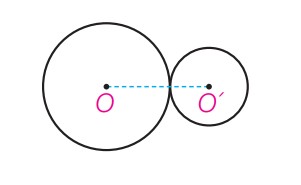
\(d = R + R'\)
دو دایره متقاطع
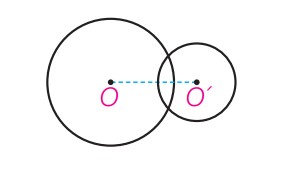
\(R - R'\langle d\langle R + R'\)
دو دایره مماس درون

\(d = R - R'\)
دو دایره متداخل
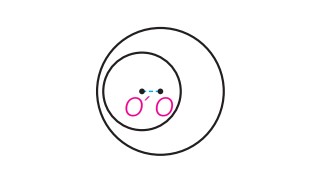
\(d\langle R - R'\)
دایره های هم مرکز
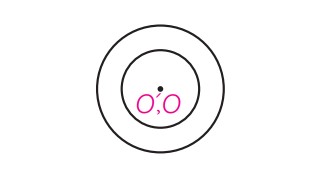
\(d = 0\)
مماس مشترک دو دایره
خطی است که بر هر دو دایره مماس است.
مماس مشترک خارجی
اگر دو دایره در یک طرف خط مماس باشند، این خط را مماس مشترک خارجی می گویند.

مماس مشترک داخلی
اگر دو دایره در طورف خط مماس باشند، این خط را مماس مشترک داخلی می گویند.

طول مماس مشترک ها به صورت زیر محاسبه می شوند:
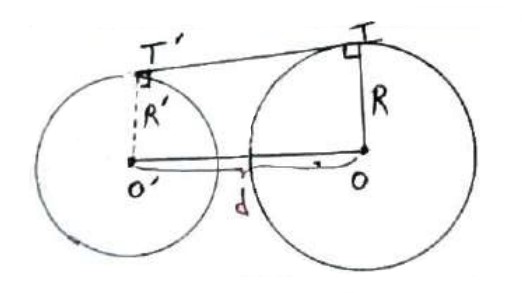
طول مماس مشترک خارجی: \(TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} \)
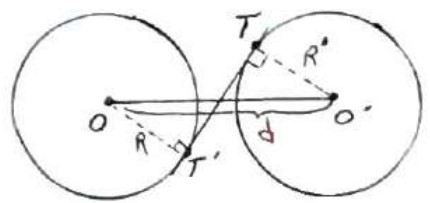
طول مماس مشترک داخلی: \(TT' = \sqrt {{d^2} - {{\left( {R + R'} \right)}^2}} \)
1 طول مماس مشترک های داخلی و خارجی دو دایره \(C\left( {O,7} \right)\) و \(C'\left( {O',1} \right)\) را با فرض \(OO' = 10\) بدست آورید.
\(OO' = d = 10\)
طول مماس مشترک خارجی:
\(\begin{array}{l}TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} = \sqrt {{{10}^2} - {{\left( {7 - 1} \right)}^2}} \\\\ \Rightarrow \sqrt {100 - 36} = \sqrt {64} = 8\end{array}\)
طول مماس مشترک داخلی:
\(\begin{array}{l}TT' = \sqrt {{d^2} - {{\left( {R + R'} \right)}^2}} = \sqrt {{{10}^2} - {{\left( {7 + 1} \right)}^2}} \\\\ \Rightarrow \sqrt {100 - 64} = \sqrt {36} = 6\end{array}\)
2 طول خط المرکزین دو دایره مماس درون 2 سانتی متر و مساحت ناحیه محدود بین آنها \(16\pi \) سانتی متر مربع است. طول و شعاع های دو دایره را بدست آورید.
\(\begin{array}{l}OO' = 2 \Rightarrow R - R' = 2\\\\S - S' = \pi {R^2} - \pi {{R'}^2} = 16\pi \\\\ \Rightarrow {R^2} - {{R'}^2} = 16\\\\ \Rightarrow \left( {R - R'} \right)\left( {R + R'} \right) = 16\\\\ \Rightarrow 2\left( {R + R'} \right) = 16 \Rightarrow \left( {R + R'} \right) = 8\\\\R - R' = 2\\\\R + R' = 8\\\\ \Rightarrow R = 5\;,\;R' = 3\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
چند ضلعی محاطی
چند ضلعی محاطی
یک چند ضلعی را محاطی (محاط در دایره) می گوییم هرگاه تمام راس های آن روی محیط یک دایره باشند. (در این صورت دایره را، دایره محیطی آن چند ضلعی می نامیم.)
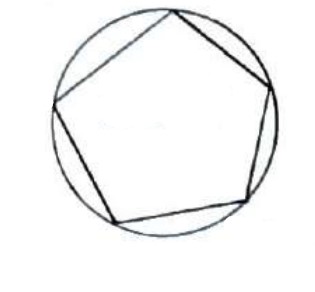
مثال
ثابت کنید مرکز دایره محیطی یک چند ضلعی، نقطه همرسی عمود منصف های همه اضلاع آن می باشد.
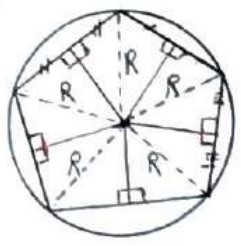
اثبات
واضح است که اگر نقطه O مرکز دایره محیطی چند ضلعی باشد، فاصله آن از تمام راس ها همواره برابر با شعاع دایره محیطی (R) است. بنابراین، این نقطه از دو سر هر ضلع چند ضلعی به یک فاصله است و لذا روی عمود منصف هر کدام از اضلاع قرار دارد.
عکس مطلب بالا نیز به طور مشابه اثبات می شود.
یعنی اگر به مرکز نقطه همرسی عمود منصف های اضلاع یک چند ضلعی دایره ای رسم کنیم، این دایره از تمام راس های چند ضلعی می گذرد.
در نتیجه یک چند ضلعی، محاطی است اگر و فقط اگر عمود منصف های همه اضلاع آن در یک نقطه همرس باشند.
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
چند ضلعی محیطی
چند ضلعی محیطی
یک چند ضلعی را محیطی (محیط بر دایره) می گوییم، هر گاه تمام ضلع های آن بر یک دایره مماس باشند. (در اینصورت دایره را، دایره محاطی آن چند ضلعی می نامیم.)
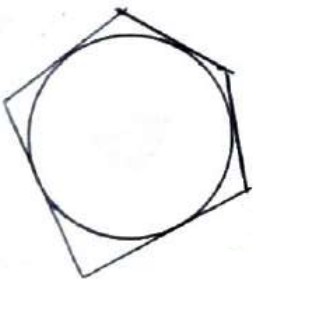
هر نقطه روی نیم ساز هر زاویه، از دو ضلع آن زاویه به یک فاصله است و برعکس اگر نقطه ای از دو ضلع یک زاویه به یک فاصله باشد، روی نیم ساز آن زاویه است.
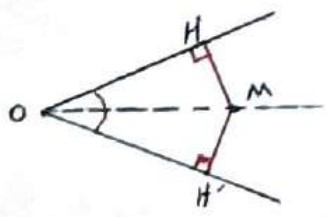
\(MH = MH'\)
مثال
ثابت کنید مرکز دایره محاطی یک چند ضلعی، نقطه همرسی نیم ساز های داخلی همه زاویه های آن می باشد.
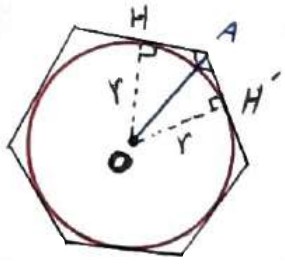
اثبات
واضح است که اگر نقطه O مرکز دایره محاطی چند ضلعی باشد، فاصله آن از تمام ضلع ها برابر با شعاع دایره محاطی (r) است.
توجه کنید که اگر از نقطه O به هر نقطه تماس وصل کنیم، شعاع در نقطه تماس بر خط مماس یعنی بر چند ضلعی، عمود است و لذا فاصله O از آن ضلع را نشان می دهد.
بنابراین این نقطه از دو ضلع هر زاویه داخلی چند ضلعی به یک فاصله است و در نتیجه روی نیمساز داخلی هر زاویه داخلی چند ضلعی قرار دارد.
یک چند ضلعی محیطی است اگر و تنها اگر همه نیم ساز های زاویه های داخلی آن در یک نقطه همرس باشند، این نقطه مرکز دایره محاطی چند ضلعی است.
اگر S و 2P به ترتیب مساحت و محیط یک چند ضلعی محیطی و r شعاع دایره محاطی آن باشد، آنگاه: \(S = rP\)
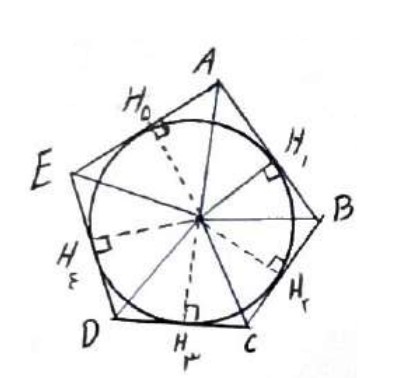
اثبات
با توجه به شکل
مساحت چند ضلعی برابر است با مجموع مساحت های مثلث های داخل
\(\begin{array}{l}{S_T} = {S_{A\mathop O\limits^\Delta B}} + {S_{B\mathop O\limits^\Delta C}} + {S_{C\mathop O\limits^\Delta D}} + {S_{D\mathop O\limits^\Delta E}} + {S_{E\mathop O\limits^\Delta A}}\\\\{S_T} = \left( {\frac{1}{2}O{H_1} \times AB} \right) + \left( {\frac{1}{2}O{H_2} \times BC} \right) + \left( {\frac{1}{2}O{H_3} \times DC} \right) + \left( {\frac{1}{2}O{H_4} \times DE} \right) + \left( {\frac{1}{2}O{H_5} \times AE} \right)\\\\ \Rightarrow O{H_1} = O{H_2} = \cdots = r\\\\ \Rightarrow {S_T} = r\left( {\frac{{AB + BC + DC + DE + AE}}{2}} \right) = rP\end{array}\)
تهیه کننده: امیرحسین مطلبی
دایره محیطی مثلث
دایره محیطی مثلث
دایره ای که از سه راس یک مثلث می گذرد، دایره محیطی مثلث نامیده می شود. (مرکز دایره محیطی مثلث نقطه همرسی عمود منصف است.)
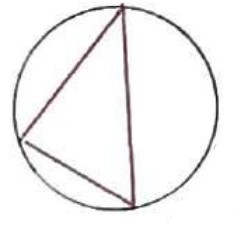
مثال
ثابت کنید مثلث همواره محاطی است.
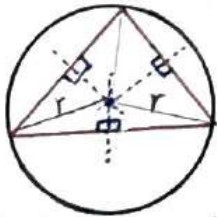
اثبات
می دانیم سه عمود منصف ضلع های هر مثلث همرس می باشند و این نقطه همرسی تنها نقطه ای است که از سه راس یک مثلث به یک فاصله است، پس اگر دایره ای به مرکز نقطه تلاقی سه عمود منصف و به شعاع فاصله این نقطه تا یک راس رسم کنیم، این دایره از هر سه راس مثلث می گذرد. (دایره محیطی مثلث) در نتیجه مثلث همواره محاطی است.
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
دایره محاطی مثلث
دایره محاطی مثلث
دایره ای که بر هر سه ضلع مثلث مماس می باشد، دایره ی محاطی داخلی مثلث نامیده می شود. (مرکز دایره محاطی مثلث نقطه همرسی نیم ساز های زاویه های داخلی مثلث است.)
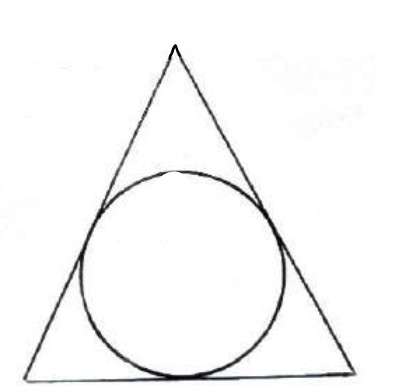
مثال
ثابت کنید مثلث همواره محیطی است.
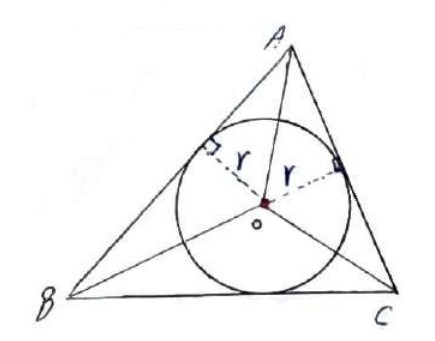
اثبات
می دانیم سه نیم ساز داخلی هر مثلث همواره در یک مثلث همرس اند، پس اگر به مرکز این نقطه همرسی و به شعاع فاصله این نقطه تا یک ضلع مثلث دایره ای رسم کنیم بر هر سه ضلع مثلث مماس خواهد شد. بنابراین مثلث همواره محیطی است.
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
دایره محاطی خارجی
دایره محاطی خارجی
دایره ای که بر یک ضلع و امتداد دو ضلع دیگر آن مماس باشد، دایره محاطی خارجی مثلث نامیده می شود.
هر مثلث سه دایره محاطی خارجی دارد.
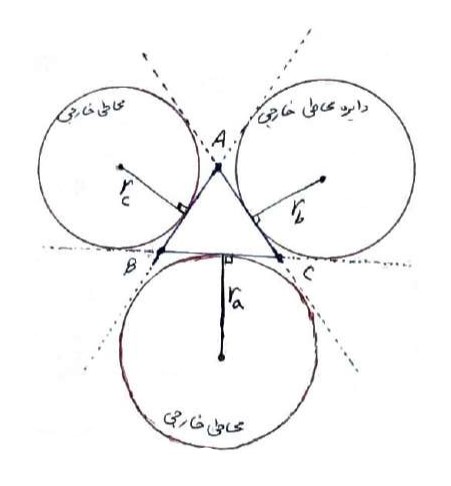
مرکز دایره محاطی خارجی مثلث، نقطه همرسی دو نیمساز خارجی و نیم ساز داخلی راس سوم است.
1 با توجه به مفهوم دایره محاطی خارجی، مثلث ABC ثابت کنید:
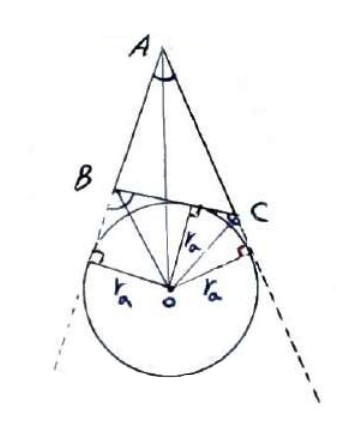
\({S_{ABC}} = {r_a}\left( {P - a} \right) \Rightarrow {r_a} = \frac{S}{{P - a}}\)
اثبات
\(\begin{array}{l}{S_{A\mathop B\limits^\Delta C}} = S = {S_{O\mathop A\limits^\Delta B}} + {S_{O\mathop A\limits^\Delta C}} - {S_{O\mathop B\limits^\Delta C}}\\\\ \Rightarrow \left( {\frac{1}{2}{r_a} \times AB} \right) + \left( {\frac{1}{2}{r_a} \times AC} \right) - \left( {\frac{1}{2}{r_a} \times BC} \right)\\\\ \Rightarrow S = {r_a}\left( {\frac{{AB + AC - BC}}{2}} \right)\\\\ \Rightarrow {r_a}\left( {\frac{{AB + AC + BC - BC - BC}}{2}} \right)\\\\ \Rightarrow {r_a}\left( {\frac{{2P - 2a}}{2}} \right) \Rightarrow {r_a} = \frac{S}{{P - a}}\end{array}\)
2 اگر \({r_a}\)، \({r_b}\) و \({r_c}\) شعاع های سه دایره محاطی خارجی مثلث \(A\mathop B\limits^\Delta C\) و r شعاع دایره محاطی داخلی باشد، نشان دهید:
\(\frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}} = \frac{1}{r}\)
با توجه به اینکه \({r_a} = \frac{S}{{P - a}}\) ، بنابراین:
\(\begin{array}{l}\frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}} = \frac{{P - a}}{S} + \frac{{P - b}}{S} + \frac{{P - c}}{S}\\\\ \Rightarrow \frac{{3P - \left( {a + b + c} \right)}}{S} = \frac{{3P - 2P}}{S} = \frac{P}{S} = \frac{1}{r}\end{array}\)
3 اگر \({h_a}\) ، \({h_b}\) و \({h_c}\) ارتفاع های نظیر سه ضلع مثلث باشند، نشان دهید:
\(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\)
می دانیم مساحت مثلث ABC با توجه به ارتفاع های سه ضلع آن به صورت زیر بدست می آید:
\(\begin{array}{l}{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}{h_a} \times a = \frac{1}{2}{h_b} \times b = \frac{1}{2}{h_c} \times c\\\\ \Rightarrow 2S = {h_a} \times a = {h_b} \times b = {h_c} \times c\\\\ \Rightarrow {h_a} = \frac{{2S}}{a}\;,\;{h_b} = \frac{{2S}}{b}\;,\;{h_c} = \frac{{2S}}{c}\\\\ \Rightarrow \frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{{\frac{{2S}}{a}}} + \frac{1}{{\frac{{2S}}{b}}} + \frac{1}{{\frac{{2S}}{c}}}\\\\ \Rightarrow \frac{a}{{2S}} + \frac{b}{{2S}} + \frac{c}{{2S}} = \frac{{a + b + c}}{{2S}} = \frac{{2P}}{{2S}} = \frac{1}{r}\end{array}\)
تهیه کننده: امیرحسین مطلبی
چهار ضلعی های محاطی و محیطی
چهار ضلعی های محاطی و محیطی
بر خلاف مثلث، همه چند ضلعی های دیگر، لزوما محاطی و محیطی نیستند. در این بخش به شرایط محاطی و یا محیطی بودن چهار ضلعی می پردازیم.
قضیه 1
یک چهار ضلعی محاطی است اگر و فقط اگر دو زاویه مقابل آن مکمل باشد.
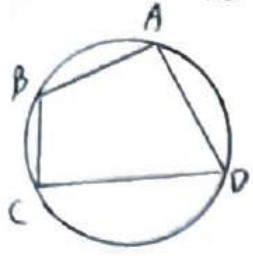
فرض می کنیم ABCD محاطی است.
حکم: \(\begin{array}{l}\hat A + \hat C = 180\\\\\hat B + \hat D = 180\end{array}\)
اثبات
\(\begin{array}{l}\hat A = \frac{{BCD}}{2}\\\\\hat C = \frac{{BAD}}{2}\\\\ \Rightarrow \hat A + \hat C = \frac{{BCD + BAD}}{2} = \frac{{360}}{2} = {180^0}\\\\\hat B = \frac{{ADC}}{2}\\\\\hat D = \frac{{ABC}}{2}\\\\ \Rightarrow \hat B + \hat D = \frac{{ADC + ABC}}{2} = \frac{{360}}{2} = {180^0}\end{array}\)
مثال
با توجه به شکل زیر اندازه X و Y را پیدا کنید.
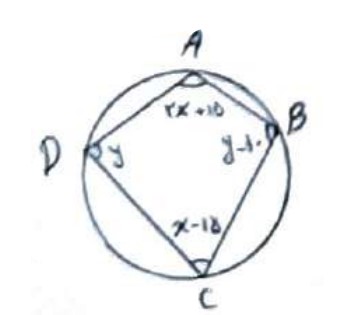
چون چهار ضلعی ABCD محاطی است، زوایای رو به رو مکمل یکدیگرند:
\(\begin{array}{l}\hat A + \hat C = 180 \Rightarrow 2x + 15 + x - 15 = 180\\\\ \Rightarrow 3x = 180 \Rightarrow x = 60\\\\\hat B + \hat D = 180 \Rightarrow y - 10 + y = 180\\\\ \Rightarrow 2y = 190 \Rightarrow y = 95\end{array}\)
قضیه 2
در یک چهار ضلعی محیطی مجموع اندازه های دو ضلع مقابل، برابر مجموع اندازه های دو ضلع مقابل دیگر است. (عکس قضیه نیز برقرار است.)
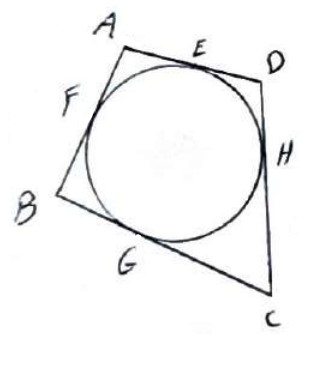
حکم: \(AB + CD = AD + BC\)
اثبات
قبلا دیدیم از هر نقطه بیرون دایره، دو مماس بر دایره رسم کنیم، اندازه های این دو مماس برابرند.
\(\begin{array}{l}AF = AE\\\\BF = BG\\\\CH = CG\\\\DH = ED\\\\ \Rightarrow AF + BF + CH + DH = AE + ED + BG + CG\\\\ \Rightarrow AB + CD = AD + BC\end{array}\)
چند ضلعی منتظم
یک چند ضلعی محدب را منتظم گوییم هر گاه تمام ضلع های آن هم اندازه و تمام زاویه های آن نیز هم اندازه باشند.
هر چند ضلعی منتظم هم محاطی است و هم محیطی.
1 فرض کنیم اندازه ضلع چهارم برابر x باشد، پس اندازه های اضلاع چهارضلعی به ترتیب 7، 11، 16 و x است. اندازه ضلع مجهول را بدست آورید.
طبق قضیه: \(x + 11 = 16 + 7 \Rightarrow x = 23 - 11 = 12\)
2 ثابت کنید یک ذوزنقه محاطی است، اگر و فقط اگر متساوی الساقین باشد.
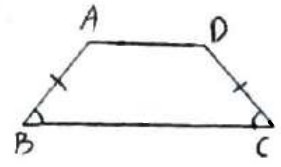
فرض کنیم ذوزنقه ABCD متساوی الساقین باشد. (\(AB = CD\;,\;AD\parallel BC\) )
نشان می دهیم محاطی است یعنی زاویه های مقابل مکمل اند. (\(\hat A + \hat C = \hat B + \hat D = {180^0}\) )
\(\begin{array}{l}ABCD \Rightarrow \hat B = \hat C\\\\AD\parallel BC \Rightarrow \hat A + \hat B = {180^0}\\\\ \Rightarrow \hat A + \hat C = {180^0} = \hat B + \hat D\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم



1736019749.png)