درسنامه کامل هندسه یازدهم فصل 3 روابط طولی در مثلث
تعداد بازدید : 7.59Mخلاصه نکات هندسه یازدهم فصل 3 روابط طولی در مثلث - درسنامه شب امتحان هندسه یازدهم فصل 3 روابط طولی در مثلث - جزوه شب امتحان هندسه یازدهم نوبت اول فصل 3 روابط طولی در مثلث
روابط طولی در مثلث قائم الزاویه
روابط طولی در مثلث قائم الزاویه
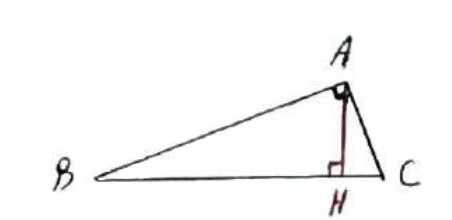
در هر مثلث قائم الزاویه، هر ضلع قائم واسطه هندسی وتر و تصویر آن ضلع بر وتر است:
1) \(A{B^2} = BC \times BH\)
2) \(A{C^2} = BC \times CH\)
ارتفاع های وارد بر وتر واسطه هندسی قطعه های ایجاد شده، روی وتر است:
3) \(A{H^2} = BH \times CH\)
رابطه فیثاغورس:
4) \(B{C^2} = A{B^2} + A{C^2}\)
حاصل ضرب اضلاع قائمه برابر است با حاصل ضرب وتر و ارتفاع وارد بر وتر:
5) \(AB \times AC = BC \times AH\)
ثابت کنید در هر مثلث قائم الزاویه ABC که \(\hat A = {90^0}\) با ارتفاع \(AH = {h_a}\) داریم:
\(\frac{1}{{h_a^2}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)
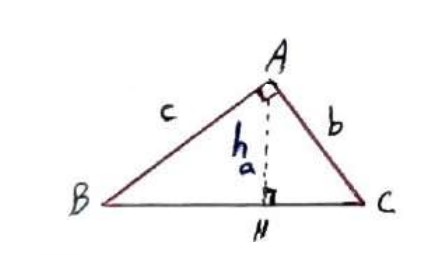
\(\begin{array}{l}\frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{{{c^2} + {b^2}}}{{{b^2}{c^2}}} = \frac{{{a^2}}}{{{b^2}{c^2}}}\\\\ \Rightarrow {\left( {\frac{a}{{bc}}} \right)^2} = {\left( {\frac{a}{{a{h_a}}}} \right)^2} = \frac{1}{{h_a^2}}\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
قضیه سینوس ها
قضیه سینوس ها
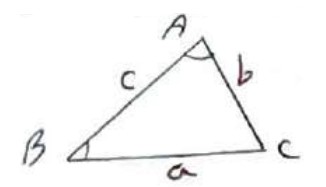
در مثلث دلخواه ABC داریم:
\(\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = \frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = \frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\)
اثبات:
حالت اول: \(A < {90^0}\)
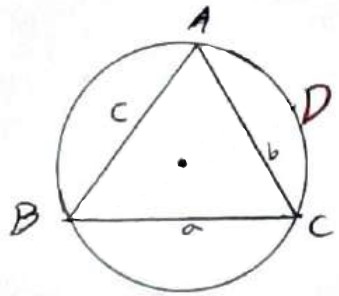
قطر BD را رسم می کنیم و D را به A وصل می کنیم. دو زاویه D و C محاطی و رو به رو به کمان AB هستند، لذا با هم برابر هستند:
\(\hat D = \hat C = \frac{{AB}}{2}\)
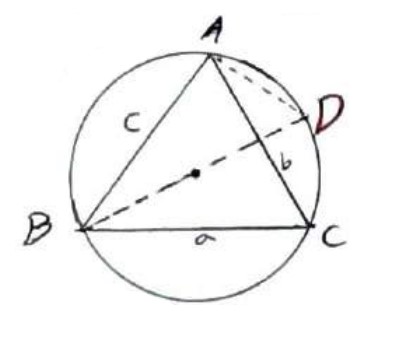
\(\begin{array}{l}\mathop {BAD}\limits^\Delta = {90^0}\\\\{\mathop{\rm Sin}\nolimits} D = \frac{c}{{BD}} \Rightarrow {\mathop{\rm Sin}\nolimits} C = \frac{c}{{BD}}\\\\ \Rightarrow \frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = BD = 2R\\\\\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R\;,\;\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R\\\\ \Rightarrow \frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = \frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = \frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\end{array}\)
حالت دوم: \(A > {90^0}\)
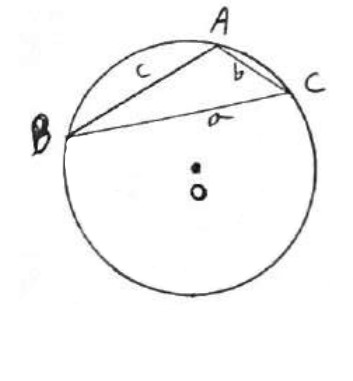
نقطه دلخواه \(A'\) روی کمان BC را به B و C وصل می کنیم.
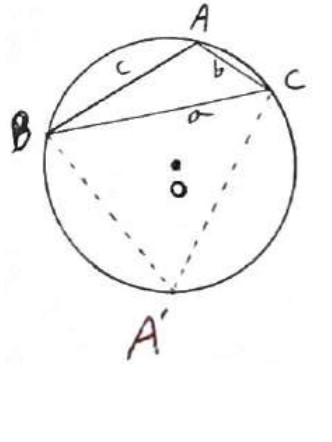
A و \(A'\) مکمل یکدیگرند یعنی \(\hat A + \hat A' = {180^0}\) زیرا \(ABA'C\) چهار ضلعی محاطی است پس قضایای اثبات شده زاویه های مقابل مکمل اند.
\(\begin{array}{l}\hat A + \hat A' = {180^0} \Rightarrow A > {90^0} \Rightarrow A' < {90^0}\\\\\frac{a}{{{\mathop{\rm Sin}\nolimits} A'}} = 2R\\\\ \Rightarrow {\mathop{\rm Sin}\nolimits} A = {\mathop{\rm Sin}\nolimits} \left( {180 - A'} \right) = {\mathop{\rm Sin}\nolimits} A'\\\\ \Rightarrow \frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R\;,\;\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R\;,\;\frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\end{array}\)
در مثلث ABC، \(BC = 10\) ، \(\hat A = {120^0}\) و \(AC = \frac{{10\sqrt 6 }}{3}\) مقدار شعاع دایره محیطی مثلث و اندازه زاویه های B و C را بدست آورید.
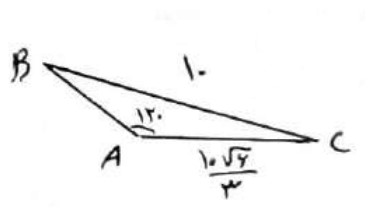
\(\begin{array}{l}\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R \Rightarrow \frac{{10}}{{\frac{{\sqrt 3 }}{2}}} = 2R \Rightarrow \frac{{20}}{{\sqrt 3 }} = 2R\\\\ \Rightarrow R = \frac{{10}}{{\sqrt 3 }}\\\\\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R \Rightarrow \frac{{\frac{{10\sqrt 6 }}{3}}}{{{\mathop{\rm Sin}\nolimits} B}} = 2\frac{{10}}{{\sqrt 3 }}\\\\ \Rightarrow {\mathop{\rm Sin}\nolimits} B = \frac{{10 \times 3\sqrt 2 }}{{3 \times 20}} = \frac{{\sqrt 2 }}{2} \Rightarrow \hat B = {45^0}\\\\\hat C = 180 - \left( {\hat B + \hat A} \right) = 180 - 165 = {15^0}\end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
قضیه کسینوس ها
قضیه کسینوس ها
از قبل می دانیم در مثلث قائم الزاویه با داشتن دو ضلع قائمه از رابطه فیثاغورس می توان ضلع سوم را بدست آورد.
رابطه فیثاغورس: \({a^2} = {b^2} + {c^2}\)
در هر مثلث، مربع اندازه هر ضلع برابر است با مجموع مربع های اندازه های دو ضلع دیگر منهای دو برابر حاصل ضرب آنها در کسینوس زاویه بین آنها.
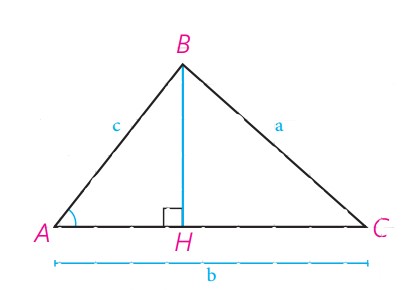
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc{\mathop{\rm Cos}\nolimits} A\\\\{b^2} = {a^2} + {c^2} - 2ac{\mathop{\rm Cos}\nolimits} B\\\\{c^2} = {a^2} + {b^2} - 2ab{\mathop{\rm Cos}\nolimits} C\end{array}\)
اثبات
رابطه اول را ثابت می کنیم دو رابطه دیگر به طور مشابه اثبات می شوند.
حالت اول در مثلث ABC زاویه \(\hat A < {90^0}\)
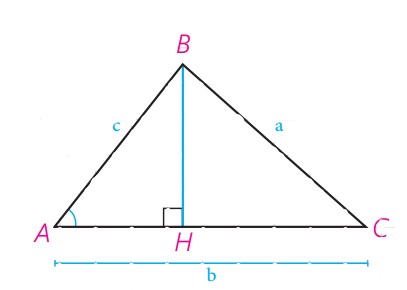
\(\begin{array}{l}\mathop {ABH}\limits^\Delta :{\mathop{\rm Cos}\nolimits} A = \frac{{AH}}{c} \Rightarrow AH = c \times {\mathop{\rm Cos}\nolimits} A\\\\CH = b - AH \Rightarrow CH = b - c{\mathop{\rm Cos}\nolimits} A\\\\{\mathop{\rm Sin}\nolimits} A = \frac{{BH}}{c} \Rightarrow BH = c \times {\mathop{\rm Sin}\nolimits} A\\\\{a^2} = B{H^2} + C{H^2}\\\\ \Rightarrow {a^2} = {\left( {c \times {\mathop{\rm Sin}\nolimits} A} \right)^2} + {\left( {b - c{\mathop{\rm Cos}\nolimits} A} \right)^2}\\\\{a^2} = {c^2}{{\mathop{\rm Sin}\nolimits} ^2}A + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A + {c^2}{{\mathop{\rm Cos}\nolimits} ^2}A\\\\{a^2} = {c^2}\left( {{{{\mathop{\rm Sin}\nolimits} }^2}A + {{{\mathop{\rm Cos}\nolimits} }^2}A} \right) + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\\\\{a^2} = {c^2} + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\end{array}\)
حالت دوم در مثلث ABC زاویه \(A > {90^0}\) باشد.
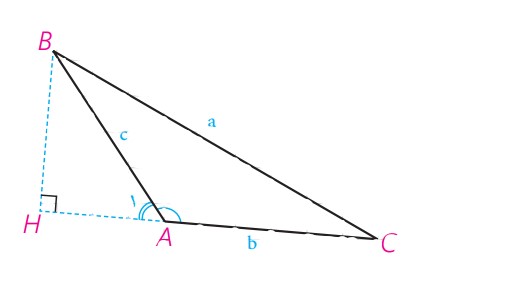
\(\begin{array}{l}{A_1} = 180 - A\\\\ \Rightarrow {\mathop{\rm Sin}\nolimits} {A_1} = {\mathop{\rm Sin}\nolimits} \left( {180 - A} \right) = {\mathop{\rm Sin}\nolimits} A\\\\ \Rightarrow {\mathop{\rm Cos}\nolimits} {A_1} = {\mathop{\rm Cos}\nolimits} \left( {180 - A} \right) = - {\mathop{\rm Cos}\nolimits} A\\\\{\mathop{\rm Cos}\nolimits} {A_1} = \frac{{AH}}{C} \Rightarrow AH = c \times {\mathop{\rm Cos}\nolimits} {A_1}\\\\ \Rightarrow AH = - c \times {\mathop{\rm Cos}\nolimits} A\\\\ \Rightarrow CH = b - c{\mathop{\rm Cos}\nolimits} A\\\\ \Rightarrow BH = c \times {\mathop{\rm Sin}\nolimits} A\\\\B{C^2} = B{H^2} + C{H^2}\\\\{a^2} = {\left( {C{\mathop{\rm Sin}\nolimits} A} \right)^2} + {\left( {b - c{\mathop{\rm Cos}\nolimits} A} \right)^2}\\\\{a^2} = {c^2}{{\mathop{\rm Sin}\nolimits} ^2}A + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A + {c^2}{{\mathop{\rm Cos}\nolimits} ^2}A\\\\{a^2} = {c^2}\left( {{{{\mathop{\rm Sin}\nolimits} }^2}A + {{{\mathop{\rm Cos}\nolimits} }^2}A} \right) + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\\\\ \Rightarrow {a^2} = {c^2} + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\end{array}\)
دو قایق از یک نقطه در دریاچه ای با سرعت های \(60km/h\) و \(100km/h\) و با زاویه \({120^0}\) از هم دور می شوند. نیم ساعت بعد دو قایق در چه فاصله ای از یکدیگر هستند؟
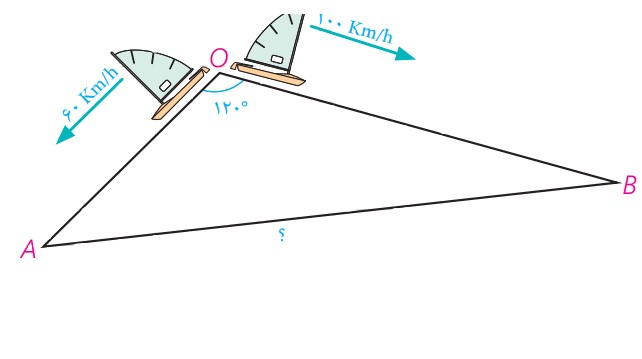
با توجه به نقطه شروع دو قایق و سرعت های ثابت، نیم ساعت بعد، مسافت طی شده توسط هر قایق محاسبه می شود:
\(\begin{array}{l}OA = 60 \times 0/5 = 30\;,\;OB = 100 \times 0/5 = 50\\\end{array}\)
حال به کمک قضیه کسینوس ها می نویسیم:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA \times {\mathop{\rm Cos}\nolimits} {120^0}\\\\A{B^2} = 900 + 2500 - 2 \times 30 \times 50\left( { - \frac{1}{2}} \right)\\\\A{B^2} = 4900 \Rightarrow AB = 70km\end{array}\)
تهیه کننده: امیرحسین مطلبی
قضیه میانه ها
قضیه میانه ها
در مثلث ABC میانه AM را رسم کرده ایم، ثابت کنید:
\({b^2} + {c^2} = 2A{M^2} + \frac{{{a^2}}}{2}\)
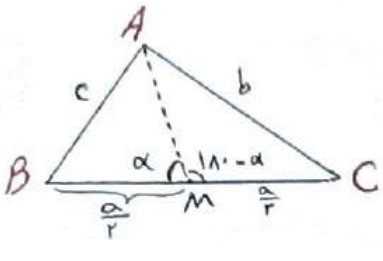
با استفاده از قضیه کسینوس ها در دو مثلث \(\mathop {ABM}\limits^\Delta \) و \(\mathop {ACM}\limits^\Delta \) داریم:
\(\begin{array}{l}\mathop {ABM}\limits^\Delta :A{B^2} = A{M^2} + B{M^2} - 2AM.BM{\mathop{\rm Cos}\nolimits} \alpha \\\\ \Rightarrow {c^2} = A{M^2} + {\left( {\frac{a}{2}} \right)^2} - 2AM.\left( {\frac{a}{2}} \right){\mathop{\rm Cos}\nolimits} \alpha \\\\\mathop {ACM}\limits^\Delta :A{C^2} = A{M^2} + C{M^2} - 2AM.CM - {\mathop{\rm Cos}\nolimits} \alpha \\\\ \Rightarrow {b^2} = A{M^2} + {\left( {\frac{a}{2}} \right)^2} + 2AM.\left( {\frac{a}{2}} \right){\mathop{\rm Cos}\nolimits} \alpha \\\\{c^2} + {b^2} = 2A{M^2} + \frac{{{a^2}}}{2}\end{array}\)
رابطه بالا برای میانه های دیگر مثلث نیز برقرار است:
\(\begin{array}{l}{a^2} + {c^2} = 2B{M^2} + \frac{{{b^2}}}{2}\\\\{a^2} + {b^2} = 2C{M^2} + \frac{{{c^2}}}{2}\end{array}\)
در مثلث ABC اگر \(AB = 4\) ، \(AC = 6\) و \(BC = 8\) باشد طول میانه AM را بدست آورید.
\(\begin{array}{l}{b^2} + {c^2} = 2A{M^2} + \frac{{{a^2}}}{2}\\\\{6^2} + {4^2} = 2A{M^2} + \frac{{{8^2}}}{2}\\\\64 + 16 = 2A{M^2} + 32\\\\A{M^2} = 8 \Rightarrow AM = \sqrt 8 \end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
قضیه نیم ساز های زوایای داخلی
قضیه نیم ساز های زوایای داخلی
در هر مثلث نیم ساز زاویه داخلی، ضلع رو به رو به آن زاویه را به نسبت اندازه های دو ضلع دیگر مثلث تقسیم می کند.
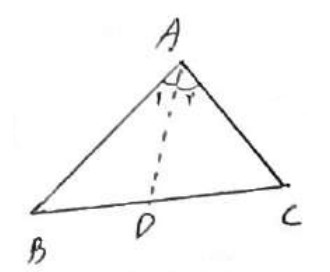
فرض: \({\hat A_1} = {\hat A_2}\)
حکم: \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\)
اثبات
از نقطه C خطی موازی با نیم ساز AD رسم می کنیم تا امتداد AB را در E قطع کند.
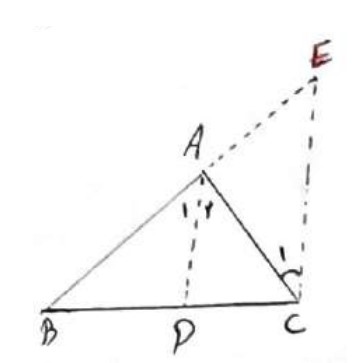
\(\begin{array}{l}AD\parallel EC \Rightarrow {{\hat A}_2} = {{\hat C}_1}\\\\AD\parallel EC \Rightarrow {{\hat A}_1} = \hat E\\\\ \Rightarrow {{\hat A}_1} = {{\hat A}_2} \Rightarrow {{\hat C}_1} = \hat E\\\\ \Rightarrow A\mathop E\limits^\Delta C \Rightarrow AE = AC\\\\\mathop {BEC}\limits^\Delta :AD\parallel EC \Rightarrow \frac{{BD}}{{DC}} = \frac{{AB}}{{AE}}\\\\ \Rightarrow AE = AC \Rightarrow \frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\end{array}\)
اندازه سه ضلع مثلث 8، 12 و 15 سانتی متر می باشند، اندازه پاره خط هایی که نیم ساز درونی زاویه بزرگتر مثلث بر ضلع مقابل آن پدید می آورد را تعیین کنید.
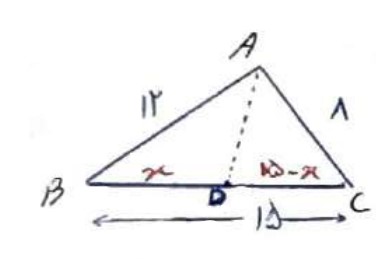
\(\begin{array}{l}\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{12}}{8}\\\\\frac{x}{{15 - x}} = \frac{3}{2} \Rightarrow 2x = 45 - 3x\\\\ \Rightarrow 5x = 45 \Rightarrow x = 9\\\\ \Rightarrow BD = 9\;,\;CD = 6\end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه یازدهم
جزوه جامع هندسه یازدهم فصل 1 دایره
جزوه جامع هندسه یازدهم فصل 2 تبدیل های هندسی و کاربردها
جزوه جامع هندسه یازدهم فصل 3 روابط طولی در مثلث
قضیه محاسبه طول نیم ساز ها
قضیه محاسبه طول نیم ساز ها
در هر مثلث، مربع اندازه هر نیم ساز داخلی برابر است با حاصل ضرب اندازه دو ضلع زاویه، منهای حاصل ضرب اندازه ی دو قطعه ای که نیم ساز روی ضلع مقابل ایجاد می کند.
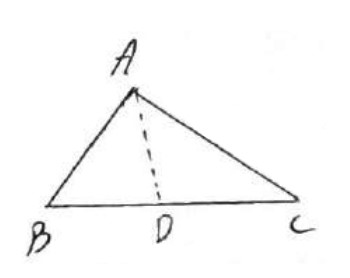
حکم: \(A{D^2} = AB \times AC - BD \times DC\)
اثبات
ابتدا دایره محیطی مثلث ABC را رسم می کنیم و نیم ساز AD را امتداد می دهیم تا دایره محیطی را در نقطه E قطع کند.
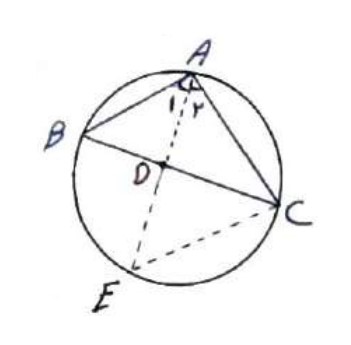
\(\begin{array}{l}AD \Rightarrow {{\hat A}_1} = {{\hat A}_2}\\\\\hat B = \hat E = \frac{{AC}}{2}\\\\\mathop {ABD}\limits^\Delta \sim \mathop {AEC}\limits^\Delta \Rightarrow \frac{{AC}}{{AD}} = \frac{{AE}}{{AB}} = \frac{{CE}}{{BD}}\\\\ \Rightarrow \frac{{AC}}{{AD}} = \frac{{AE}}{{AB}} \Rightarrow AB \times AC = AD \times AE\\\\ \Rightarrow AE = AD + DE\\\\ \Rightarrow AB \times AC = AD\left( {AD + DE} \right)\\\\ \Rightarrow AB \times AC = A{D^2}AD \times AE\\\\ \Rightarrow AD \times AE = BD \times DC\\\\ \Rightarrow AB \times AC = A{D^2}BD \times DC\\\\ \Rightarrow A{D^2} = AB \times AC - BD \times DC\end{array}\)
در مثلث ABC، \(AB = 7\) ، \(AC = 5\) و \(BC = 10\) است؛ طول نیم ساز زاویه داخلی C را بدست آورید.
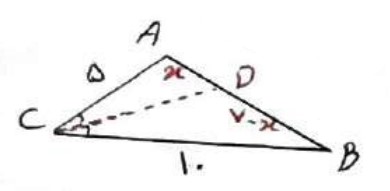
\(\begin{array}{l}\frac{{CA}}{{CB}} = \frac{{AD}}{{BD}} \Rightarrow \frac{5}{{10}} = \frac{{AD}}{{BD}} \Rightarrow \frac{1}{2} = \frac{x}{{7 - x}}\\\\ \Rightarrow 2x = 7 - x \Rightarrow x = \frac{7}{3} \Rightarrow AD = \frac{7}{3}\\\\BD = 7 - \frac{7}{3} = \frac{{14}}{3}\\\\C{D^2} = CA \times CB - AD \times BD\\\\ \Rightarrow C{D^2} = 5 \times 10 - \frac{7}{3} \times \frac{{14}}{3} = 50 - \frac{{98}}{9} = \frac{{352}}{9}\\\\ \Rightarrow CD = \frac{{\sqrt {352} }}{3}\end{array}\)
تهیه کننده: امیرحسین مطلبی
قضیه هرون
قضیه هرون
مساحت مثلث ABC با طول اضلاع a، b و c از رابطه زیر حاصل می شود:
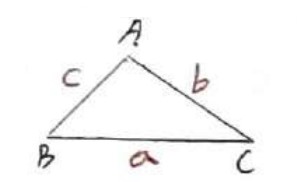
\(S = \sqrt {P\left( {P - a} \right)\left( {P - b} \right)\left( {P - c} \right)} \)
P نصف محیط است یعنی:
\(P = \frac{{a + b + c}}{2}\)
مثال
مساحت مثلثی با اضلاع 4، 5 و 7 را با استفاده از دستور هرون محاسبه کنید.
\(\begin{array}{l}P = \frac{{7 + 5 + 4}}{2} = \frac{{16}}{2} = 8\\\\S = \sqrt {P\left( {P - a} \right)\left( {P - b} \right)\left( {P - c} \right)} \\\\S = \sqrt {8\left( {8 - 4} \right)\left( {8 - 5} \right)\left( {8 - 7} \right)} \\\\S = \sqrt {8 \times 4 \times 3 \times 1} \Rightarrow S = 4\sqrt 6 \end{array}\)
قضیه
مساحت هر مثلث برابر است با نصف حاصل ضرب اندازه دو ضلع در سینوس زاویه بین آنها.
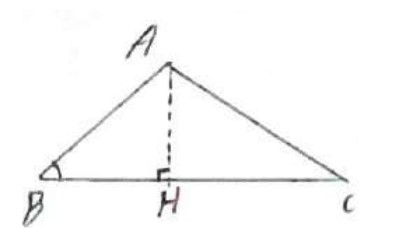
حکم: \({S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AB \times BC \times {\mathop{\rm Sin}\nolimits} B\)
اثبات
\(\begin{array}{l}{\mathop{\rm Sin}\nolimits} B = \frac{{AH}}{{AB}} \Rightarrow AH = AB \times {\mathop{\rm Sin}\nolimits} \hat B\\\\{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AH \times BC\\\\ \Rightarrow {S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AB \times BC \times {\mathop{\rm Sin}\nolimits} B\end{array}\)
به طور مشابه اثبات می شود:
\(\begin{array}{l}S = \frac{1}{2}ab{\mathop{\rm Sin}\nolimits} C\\\\S = \frac{1}{2}bc{\mathop{\rm Sin}\nolimits} A\end{array}\)
1 چهار ضلعی ABCD که در آن \(\hat A = {90^0}\) است یک زمین کشاورزی را نشان می دهد مساحت این زمین را بدست آورید.
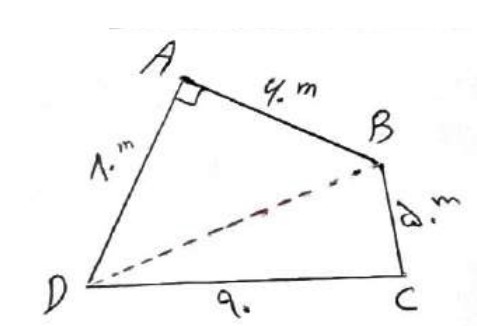
\(\begin{array}{l}B{D^2} = {80^2} + {60^2} \Rightarrow BD = \sqrt {10000} = 100\\\\{P_{B\mathop C\limits^\Delta D}} = \frac{{50 + 90 + 100}}{2} = 120\\\\{S_{A\mathop B\limits^\Delta D}} = \frac{1}{2} \times 60 \times 80 = 2400\\\\{S_{B\mathop C\limits^\Delta D}} = \sqrt {P\left( {P - a} \right)\left( {P - b} \right)\left( {P - c} \right)} \\\\ \Rightarrow \sqrt {120\left( {120 - 50} \right)\left( {120 - 90} \right)\left( {120 - 100} \right)} \\\\ \Rightarrow \sqrt {120 \times 20 \times 30 \times 70} = 600\sqrt {14} \\\\{S_T} = 2400 + 600\sqrt {14} \simeq 4650{m^2}\end{array}\)
2 مساحت مثلث زیر را بدست آورید.
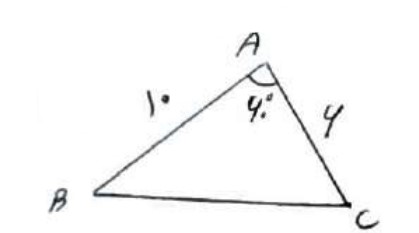
\(\begin{array}{l}{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2} \times 6 \times 10 \times {\mathop{\rm Sin}\nolimits} {60^0}\\\\{S_{A\mathop B\limits^\Delta C}} = 3 \times 10 \times \frac{{\sqrt 3 }}{2} = 15\sqrt 3 \end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم



1736019749.png)















