درسنامه کامل هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
تعداد بازدید : 7.59Mخلاصه نکات هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی - درسنامه شب امتحان هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی - جزوه شب امتحان هندسه دوازدهم نوبت اول فصل 2 آشنایی با مقاطع مخروطی
مکان هندسی
مکان هندسی
مکان هندسی مجموعه نقاطی از صفحه یا فضا است که:
- دارای یک ویژگی مشترک باشند.
- هر نقطه که این ویژگی مشترک را داشته باشد عضو مجموعه نقاط مورد نظر باشد.
مکان هندسی های مهم و معروف
1) مکان هندسی نقاطی از صفحه که از دو سر پاره خط AB به یک فاصله اند عمود منصف پاره خط AB است.
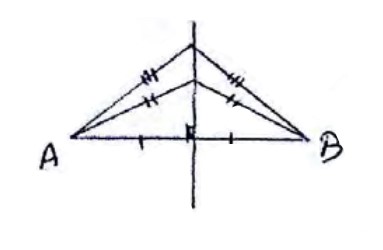
2) مکان هندسی نقاطی از صفحه که از دو ضلع یک زاویه به یک فاصله اند، نیمساز زاویه مورد نظر است.
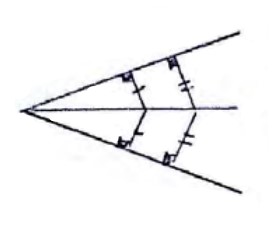
3) مکان هندسی نقاطی از صفحه که از دو خط موازی به یک فاصله اند، خطی است موازی با دو خط و در وسط آنها.
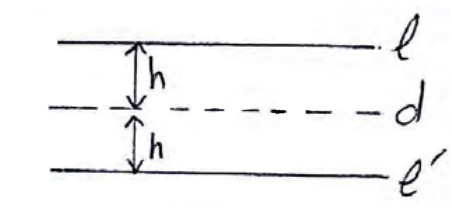
4) مکان هندسی نقاطی از صفحه که از خط L به فاصله ثابت h باشند، دو خط d و \(d'\) به موازات L و در طرفین خط L است.
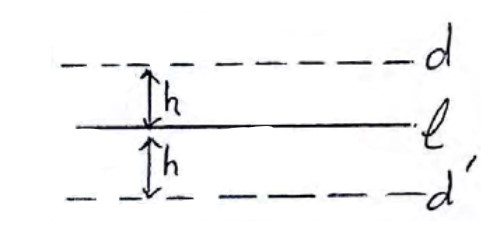
5) مکان هندسی نقاطی از صفحه که از دو خط متقاطع L و \(L'\) به یک فاصله باشند، نیمساز های زوایای بین L و \(L'\) است که بر هم عمودند.
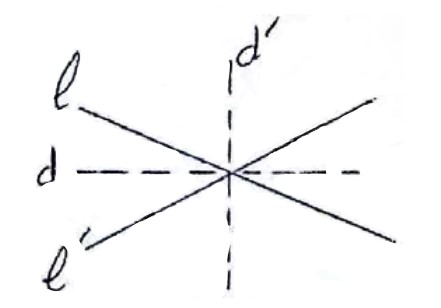
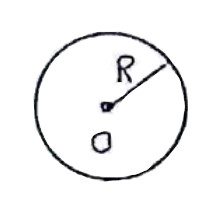
6) مکان هندسی نقاطی از صفحه که از یک نقطه معلوم O به فاصله ثابت R هستند دایره ای به مرکز O و شعاع R است.
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
رویه مخروطی
رویه مخروطی
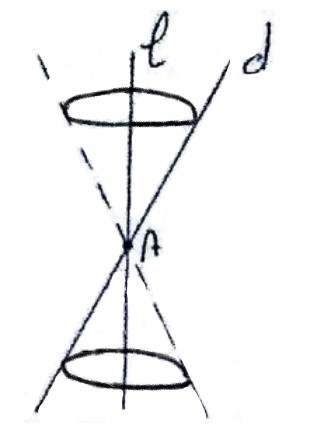
اگر دو خط d و L در نقطه A متقاطع باشند؛ سطح حاصل از دوران خط d حول خط L را یک رویه مخروطی (سطح مخروطی) می گویند. نقطه A را راس، خط L را محور و خط d را مولد سطح مخروطی می نامند.
مقاطع مخروطی
از برخورد یک صفحه با رویه مخروطی شکل بدست می آید که آنها را مقاطع مخروطی می نامیم که عبارت اند از:
دایره:
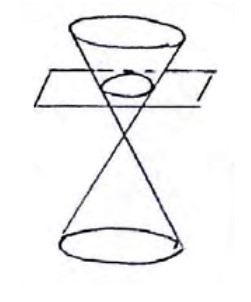
بیضی:
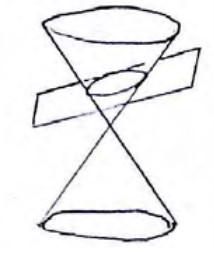
سهمی:
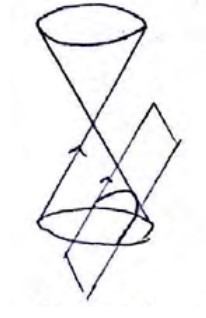
هذلولی:
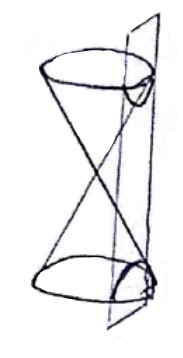
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه دوازدهم
جزوه جامع هندسه دوازدهم فصل 1 ماتریس و کاربردها
جزوه جامع هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
جزوه جامع هندسه دوازدهم فصل 3 بردارها
دایره
دایره
دایره مکان هندسی نقاطی از صفحه است که از یک نقطه ثابت به نام مرکز به فاصله ثابت (شعاع) هستند.
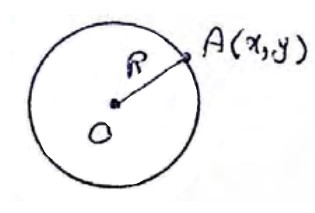
معادله استاندارد (کلاسیک) دایره
معادله دایره ای که مرکزش نقطه \(O\left[ {\begin{array}{*{20}{c}}\alpha \\\beta \end{array}} \right]\) و شعاع آن برابر R باشد از فرمول زیر به دست می آید:
\({\left( {x - \alpha } \right)^2} + {\left( {y - \beta } \right)^2} = {R^2}\)
اثبات:
\(\begin{array}{l}O\left[ {\begin{array}{*{20}{c}}\alpha \\\beta \end{array}} \right]\;\;,\;\;A\left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\\\\OA = R \Rightarrow \sqrt {{{\left( {x - \alpha } \right)}^2} + {{\left( {y - \beta } \right)}^2}} = R\\\\ \Rightarrow {\left( {x - \alpha } \right)^2} + {\left( {y - \beta } \right)^2} = {R^2}\end{array}\)
مثال
معادله دایره ای را بنویسید که مرکز آن نقطه \(O\left[ {\begin{array}{*{20}{c}}1\\2\end{array}} \right]\) بوده و \(A\left( {3, - 1} \right)\) نقطه ای از آن باشد.
\(\begin{array}{l}R = OA = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {2 - \left( { - 1} \right)} \right)}^2}} \\\\ \Rightarrow \sqrt {4 + 9} = \sqrt {13} \\\\{\left( {x - \alpha } \right)^2} + {\left( {y - \beta } \right)^2} = {R^2}\\\\ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 13\end{array}\)
معادله گسترده دایره (معادله ضمنی)
اگر معادله استاندارد دایره را باز کنیم معادله ضمنی یا گسترده دایره به صورت زیر خواهد بود:
\({x^2} + {y^2} + ax + by + c = 0\)
که در آن:
شعاع: \(R = \sqrt {\frac{{{a^2} + {b^2} - 4c}}{4}} \)
مختصات مرکز: \(O = \left( { - \frac{a}{2}\;,\; - \frac{b}{2}} \right)\)
1 مرکز و شعاع دایره \({x^2} + {y^2} - 4x - 4y + 7 = 0\) را بدست آورید.
\(\begin{array}{l}a = - 4\;\;,\;\;b = - 4\;\;,\;\;c = 7\\\\O\left[ {\begin{array}{*{20}{c}}{ - \frac{a}{2} = - \frac{{ - 4}}{2} = 2}\\{ - \frac{b}{2} = - \frac{{ - 4}}{2} = 2}\end{array}} \right] \Rightarrow O\left[ {\begin{array}{*{20}{c}}2\\2\end{array}} \right]\\\\\\R = \sqrt {\frac{{{a^2} + {b^2} - 4c}}{4}} = \sqrt {\frac{{16 + 16 - 28}}{4}} \\\\ \Rightarrow R = \sqrt {\frac{4}{4}} = 1\end{array}\)
2 مکان هندسی نقاطی مانند \(M\left( {x\;,\;y} \right)\) را پیدا کنید که فاصله آنها از نقطه \(A\left[ {\begin{array}{*{20}{c}}2\\4\end{array}} \right]\) ، \(\sqrt 2 \) برابر فاصله آنها از نقطه \(B\left[ {\begin{array}{*{20}{c}}1\\2\end{array}} \right]\) باشد.
\(\begin{array}{l}AM = \sqrt 2 BM\\\\\sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 4} \right)}^2}} = \sqrt 2 \times \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2}} \\\\ \Rightarrow {\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} = 2\left[ {{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2}} \right]\\\\ \Rightarrow {x^2} + {y^2} = 10 \Rightarrow {\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {\left( {\sqrt {10} } \right)^2}\end{array}\)
مکان مطلوب، دایره ای به مرکز مبدا مختصات و به شعاع \(\sqrt {10} \) است.
تهیه کننده: امیرحسین مطلبی
وضعیت دو دایره نسبت به هم
وضعیت دو دایره نسبت به هم
دو دایره برون هم (متخارج)
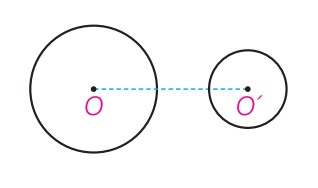
\(d > R + R'\)
دو دایره مماس برون
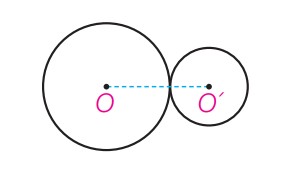
\(d = R + R'\)
دو دایره متقاطع
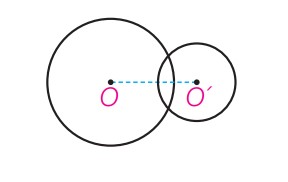
\(R - R' < d < R + R'\)
دو دایره مماس درون

\(d = R - R'\)
دو دایره متداخل
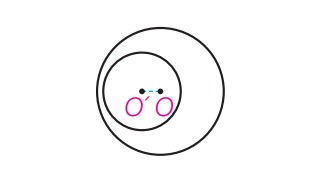
\(d < R - R'\)
دایره های هم مرکز
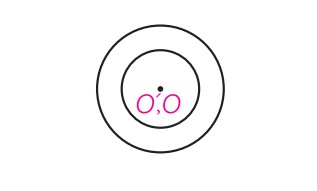
\(d = 0\)
وضعیت جفت دایره های زیر را نسبت هم مشخص کنید.
\({x^2} + {y^2} = 9\;\;\;,\;\;\;{x^2} + {y^2} - 2x + 2y - 1 = 0\)
\(\begin{array}{l}O\left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\;\;,\;\;r = 3\;\;\;,\;\;\;O'\left[ {\begin{array}{*{20}{c}}1\\{ - 1}\end{array}} \right]\;\;,\;\;r = 1\\\\d = OO' = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2}} = \sqrt 2 \\\\d = \sqrt 2 \\\\r + r' = 3 + 1 = 4\\\\r - r' = 3 - 1 = 2\\\\ \Rightarrow d > r - r'\end{array}\)
دو دایره متداخل هستند.
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
شرط دایره بودن معادله گسترده
شرط دایره بودن معادله گسترده
برای اینکه معادله گسترده \({x^2} + {y^2} + ax + by + c = 0\) معادله یک دایره باشد، باید:
- ضریب \({x^2}\) و ضریب \({y^2}\) برابر باشند. (در موقع استفاده از فرمول های مرکز و شعاع در معادله گسترده ضرایب \({x^2}\) و \({y^2}\) برابر یک باشد.)
- \({a^2} + {b^2} - 4c > 0\) (زیر رادیکال باید مثبت باشد.)
در تساوی \(m{x^2} + 5{y^2} + 20x + 10y + n + 1 = 0\) مقادیر m و n را چنان بیابید که معادله دایره باشد.
ضریب \({x^2}\) و ضریب \({y^2}\) باید برابر باشند؛ آنگاه \(m = 5\)
\(\begin{array}{l}5{x^2} + 5{y^2} + 20x + 10y + n + 1 = 0\\\\ \div 5 \Rightarrow {x^2} + {y^2} + 4x + 2y + \frac{{n + 1}}{5} = 0\\\\{a^2} + {b^2} - 4c > 0 \Rightarrow 16 + 4 - 4\left( {\frac{{n + 1}}{5}} \right) > 0\\ \Rightarrow 20 > 4\left( {\frac{{n + 1}}{5}} \right) \Rightarrow 5 > \frac{{n + 1}}{5} \Rightarrow 25 > n + 1\\\\ \Rightarrow n < 24\end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه دوازدهم
جزوه جامع هندسه دوازدهم فصل 1 ماتریس و کاربردها
جزوه جامع هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
جزوه جامع هندسه دوازدهم فصل 3 بردارها
وتر مشترک دو دایره
وتر مشترک دو دایره
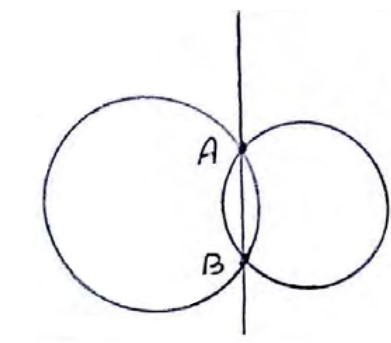
اگر دو دایره همدیگر را در دو نقطه A و B قطع کنند، به پاره خط AB وتر مشترک دو دایره می گوییم؛ برای بدست آوردن معادله وتر مشترک دو دایره می گوییم، برای بدست آوردن معادله وتر مشترک، کافی است معادله دو دایره را از هم کم کنیم. (زیرا مختصات A و B در معادله دو دایره صدق می کند، پس در تفاضل آنها هم صدق می کنند.)
معادله دایره ای را بنویسید که \(O\left[ {\begin{array}{*{20}{c}}3\\1\end{array}} \right]\) مرکز آن بوده و بر خط به معادله \(4x + 3y + 5 = 0\) مماس باشد.
\(\begin{array}{l}R = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {4\left( 3 \right) + 3\left( 1 \right) + 5} \right|}}{{\sqrt {{4^2} + {3^2}} }}\\\\ \Rightarrow \frac{{20}}{5} = 4\\\\O\left[ {\begin{array}{*{20}{c}}3\\1\end{array}} \right]\;\;,\;\;R = 4\\\\{\left( {x - \alpha } \right)^2} + {\left( {y - \beta } \right)^2} = {R^2}\\\\ \Rightarrow {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 16\end{array}\)
تهیه کننده: امیرحسین مطلبی
بیضی
بیضی
بیضی مکان هندسی نقاطی است مانند M که مجموع فواصل نقطه M از دو نقطه ثابت F و \(F'\) داخل بیضی مقدار ثابت \(2a\) است که این مقدار ثابت را قطر بزرگ بیضی می نامند.
اجزاء بیضی
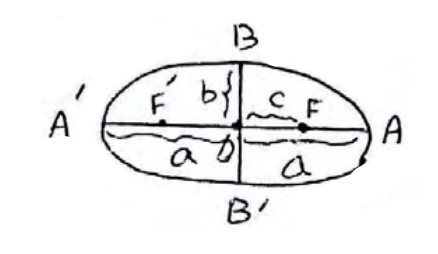
1) دو نقطه F و \(F'\) داخل بیضی را کانون های بیضی می نامند و فاصله آنها را فاصله کانونی نامیده و با \(FF' = 2c\) نشان می دهیم.
2) \(AA' = 2a\) را قطر بزرگی بیضی و \(BB' = 2b\) را قطر کوچک بیضی نامیده که همان دو محور تقارن بیضی است و محل برخورد آنها یعنی O را مرکز بیضی می نامند که همان مرکز تقارن بیضی است.
3) به مقدار ثابت \(e = \frac{c}{a}\) که \(0 < e < 1\) است که خروج از مرکز بیضی می گوییم، که همواره مثبت است. اگر e به عدد 1 نزدیک شود، بیضی کشیده تر و هر قدر e به 0 نزدیکتر شود، بیضی به دایره نزدیک تر می شود.
معادلات بیضی
1) بیضی افقی:
اگر قطر بزرگ بیضی هم راستا با محور x ها و قطر کوچک آن هم راستا با محور y ها باشد، بیضی را افقی می نامند.
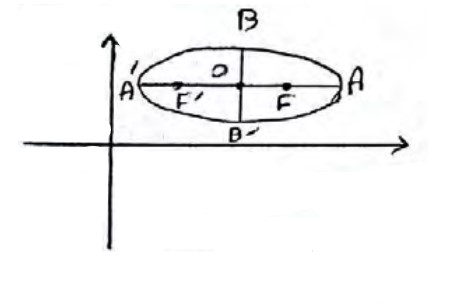
قطر بزرگ = \(AA' = 2a\)
قطر کوچک = \(BB' = 2b\)
فاصله کانونی = \(FF' = 2c\)
مرکز بیضی = \(O\left[ {\begin{array}{*{20}{c}}\alpha \\\beta \end{array}} \right]\)
خروج از مرکز بیضی = \(e = \frac{c}{a}\)
رابطه بین (\(a\;,\;b\;,\;c\) ) = \({c^2} = {a^2} - {b^2}\)
A و \(A'\) را رئوس کانونی (در امتداد کانون ها هستند.) و B و \(B'\) را رئوس غیر کانونی (در امتداد کانون ها نیستند.) می نامند.
فاصله یک راس کانونی از یک راس غیر کانونی = \(AB = \sqrt {{a^2} + {b^2}} \)
مختصات کانونی : \(\begin{array}{l}F\left[ {\begin{array}{*{20}{c}}{\alpha + c}\\\beta \end{array}} \right]\\\\F'\left[ {\begin{array}{*{20}{c}}{\alpha - c}\\\beta \end{array}} \right]\end{array}\)
معادله بیضی افقی: \(\frac{{{{\left( {x - \alpha } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - \beta } \right)}^2}}}{{{b^2}}} = 1\)
در بیضی افقی A و \(A'\) و F و \(F'\) با O هم عرض و B و \(B'\) با O هم طول هستند.
مثال
فاصله یک راس کانونی بیضی از مرکز و راس ناکانونی به ترتیب 2 و \(\sqrt 5 \) است. بیشترین فاصله نقطه M روی بیضی از یکی از کانون های بیضی چقدر است؟
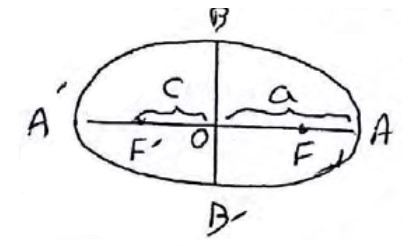
\(\begin{array}{l}a = 2\\\\AB = \sqrt 5 \Rightarrow \sqrt {{a^2} + {b^2}} = \sqrt 5 \\\\ \Rightarrow \sqrt {{2^2} + {b^2}} = \sqrt 5 \Rightarrow 4 + {b^2} = 5\\\\{b^2} = 1 \Rightarrow b = 1\\\\{c^2} = {a^2} - {b^2} = {2^2} - {1^2} = 3 \Rightarrow c = \sqrt 3 \end{array}\)
بیشترین فاصله یکی از نقاط بیضی از کانون فاصله A تا \(F'\) تا \(A'\) تا F است.
\(AF' = A'F = a + c = 2 + \sqrt 3 \)
2) بیضی قائم:
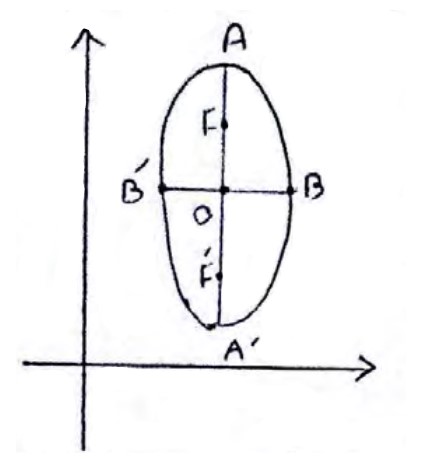
قطر بزرگ = \(AA' = 2a\)
قطر کوچک = \(BB' = 2b\)
فاصله کانونی = \(FF' = 2c\)
مرکز بیضی = \(O\left[ {\begin{array}{*{20}{c}}\alpha \\\beta \end{array}} \right]\)
خروج از مرکز بیضی = \(e = \frac{c}{a}\)
رابطه بین (\(a\;,\;b\;,\;c\) ) = \({c^2} = {a^2} - {b^2}\)
A و \(A'\) را رئوس کانونی (در امتداد کانون ها هستند.) و B و \(B'\) را رئوس غیر کانونی (در امتداد کانون ها نیستند.) می نامند.
\(\begin{array}{l}A\left[ {\begin{array}{*{20}{c}}\alpha \\{\beta + a}\end{array}} \right]\;\;,\;\;A'\left[ {\begin{array}{*{20}{c}}\alpha \\{\beta - a}\end{array}} \right]\\\\B\left[ {\begin{array}{*{20}{c}}{\alpha + b}\\\beta \end{array}} \right]\;\;,\;\;B'\left[ {\begin{array}{*{20}{c}}{\alpha - b}\\\beta \end{array}} \right]\end{array}\)
فاصله یک راس کانونی از یک راس غیر کانونی = \(AB = \sqrt {{a^2} + {b^2}} \)
مختصات کانون ها: \(\begin{array}{l}F\left[ {\begin{array}{*{20}{c}}\alpha \\{\beta + c}\end{array}} \right]\\\\F'\left[ {\begin{array}{*{20}{c}}\alpha \\{\beta - c}\end{array}} \right]\end{array}\)
معادله بیضی قائم: \(\frac{{{{\left( {x - \alpha } \right)}^2}}}{{{b^2}}} + \frac{{{{\left( {y - \beta } \right)}^2}}}{{{a^2}}} = 1\)
مخرج \({y^2}\) بزرگ تر باشد، قائم در بیضی قائم A و \(A'\) و O و F و \(F'\) هم طول و B و \(B'\) و O هم عرض هستند.
1 معادله یک بیضی به صورت \(2{x^2} + {y^2} = 10\) است، نوع بیضی را مشخص کرده سپس مختصات رئوس کانون ها، مرکز و اندازه قطر ها را بیابید.
\(\begin{array}{l}2{x^2} + {y^2} = 10 \Rightarrow \frac{{2{x^2}}}{{10}} + \frac{{{y^2}}}{{10}} = \frac{{10}}{{10}}\\\\ \Rightarrow \frac{{{x^2}}}{5} + \frac{{{y^2}}}{{10}} = 1 \Rightarrow \frac{{{{\left( {x - 0} \right)}^2}}}{5} + \frac{{{{\left( {y - 0} \right)}^2}}}{{10}} = 1\end{array}\)
بیضی قائم است. (مخرج \({y^2}\) بزرگتر است.)
\(O\left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\)
\({a^2} = 10 \Rightarrow a = \pm \sqrt {10} \Rightarrow A\left[ {\begin{array}{*{20}{c}}0\\{\sqrt {10} }\end{array}} \right]\;,\;A'\left[ {\begin{array}{*{20}{c}}0\\{ - \sqrt {10} }\end{array}} \right]\)
قطر بزرگ = \(2a = 2\sqrt {10} \)
\({b^2} = 5 \Rightarrow a = \pm \sqrt 5 \Rightarrow B\left[ {\begin{array}{*{20}{c}}{\sqrt 5 }\\0\end{array}} \right]\;,\;B'\left[ {\begin{array}{*{20}{c}}{ - \sqrt 5 }\\0\end{array}} \right]\)
قطر کوچک = \(2b = 2\sqrt 5 \)
\(\begin{array}{l}{c^2} = {a^2} - {b^2} = 10 - 5 = 5 \Rightarrow c = \pm \sqrt 5 \\\\ \Rightarrow F\left[ {\begin{array}{*{20}{c}}0\\{\sqrt 5 }\end{array}} \right]\;\;,\;\;F'\left[ {\begin{array}{*{20}{c}}0\\{ - \sqrt 5 }\end{array}} \right]\end{array}\)
2 اگر در بیضی طول قطر بزرگ دو برابر طول قطر کوچک باشد اندازه زاویه \(F\hat BF'\) چند درجه است؟
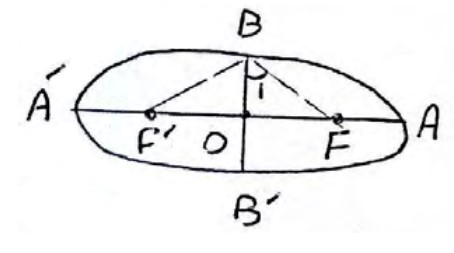
\(\begin{array}{l}2a = 2\left( {2b} \right) \Rightarrow a = 2b\\\\{c^2} = {a^2} - {b^2} = 4{b^2} - {b^2} = 3{b^2} \Rightarrow c = \sqrt 3 b\\\\\tan {{\hat B}_1} = \frac{{OF}}{{OB}} = \frac{c}{b} = \frac{{\sqrt 3 b}}{b} = \sqrt 3 \\\\ \Rightarrow {{\hat B}_1} = {60^0} \Rightarrow F\hat BF' = 2 \times 60 = {120^0}\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
سهمی
سهمی
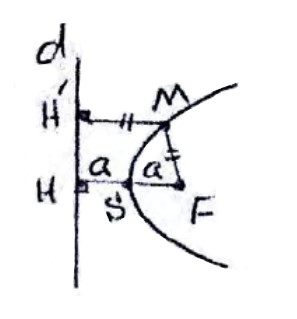
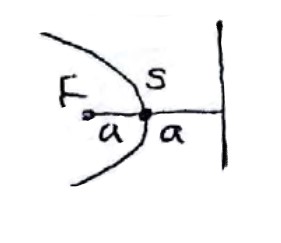
مکان هندسی تمام نقاطی از یک صفحه است که از یک خط ثابت مانند d و یک نقطه ثابت مانند F خارج از خط به یک فاصله باشند، نقطه ثابت F را کانون سهمی و خط ثابت d را خط هادی سهمی می نامند. هر نقطه دیگر هم روی سهمی در نظر بگیریم فاصله اش از F و خط هادی به یک اندازه است.
\(\begin{array}{l}MF = MH'\\\\SF = SH = a\end{array}\)
ویژگی های سهمی
1) سهمی سه جز اصلی دارد:
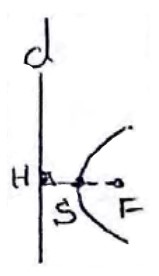
کانون سهمی: F
راس سهمی: S
خط هادی سهمی: d
2) فاصله راس سهمی تا کانون برابر است با فاصله راس سهمی تا خط هادی به عبارت دیگر راس هر سهمی وسط کانون و خط هادی قرار دارد.
\(SH = SF\)
3) فاصله راس سهمی تا کانون را فاصله کانونی سهمی نامیده و با a نشان می دهیم a را پارامتر سهمی نیز می نامند.
\(SF = SH = a\)
4) کانون همواره در دهانه سهمی قرار دارد و خط هادی همواره پشت سهمی است و سهمی هرگز خط هادی را قطع نمی کند.
5) اگر \(a\rangle 0\) باشد، دهانه سهمی در جهت مثبت محور های مختصات (راست یا بالا) باز می شود و اگر \(a\langle 0\) باشد، دهانه سهمی در جهت منفی محور های مختصات (چپ یا پایین) باز می شود.
سهمی افقی
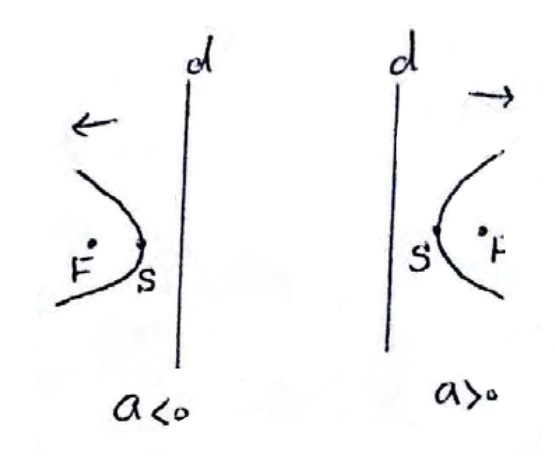
سهمی قائم
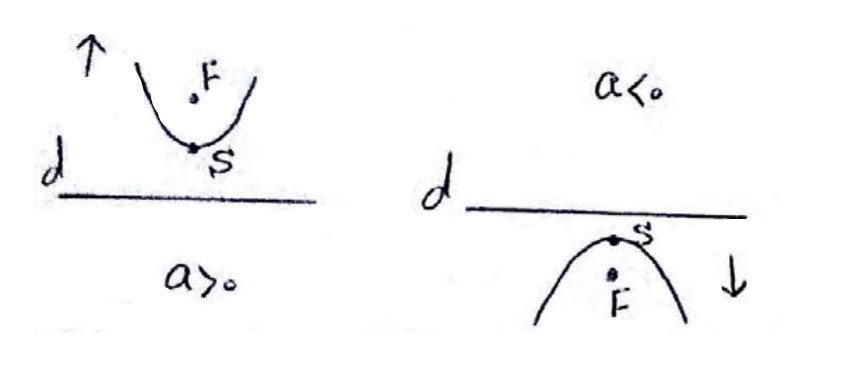
6) اگر سهمی افقی باشد خط هادی با محور y ها موازی است و معادله خط هادی به صورت \(x = k\) است.
7) اگر سهمی قائم باشد خط هادی با محور x ها موازی است و معادله خط هادی به صورت \(y = k\) است.
8) امتداد SF محور تقارن یا محور کانونی سهمی است که بر خط هادی عمود است.
اگر \(S\left( {1,2} \right)\) و \(F\left( {1, - 1} \right)\) به ترتیب راس و کانون یک سهمی باشند، معادله خط و تقارن سهمی را بنویسید.
راس و کانون را رسم می کنیم:
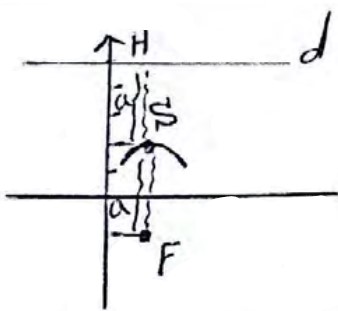
\(a = SF = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \sqrt 9 = \pm 3\)
چون دهانه سهمی رو به پایین است پس:
\(a = - 3\)
خط هادی پشت سهمی است:
\(\begin{array}{l}SF = SH = 3\\\\y = 2 + 3 \Rightarrow y = 5\end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه دوازدهم
جزوه جامع هندسه دوازدهم فصل 1 ماتریس و کاربردها
جزوه جامع هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
جزوه جامع هندسه دوازدهم فصل 3 بردارها
معادلات استاندارد سهمی
معادلات استاندارد سهمی
1) سهمی افقی باشد:
راس سهمی: \(S\left[ {\begin{array}{*{20}{c}}h\\k\end{array}} \right]\)
پارامتر: a
معادله سهمی: \({\left( {y - k} \right)^2} = 4a\left( {x - h} \right)\)
2) سهمی قائم باشد:
راس سهمی: \(S\left[ {\begin{array}{*{20}{c}}h\\k\end{array}} \right]\)
پارامتر: a
معادله سهمی: \({\left( {x - h} \right)^2} = 4a\left( {y - k} \right)\)
اگر در معادله استاندارد سهمی پرانتز ها را حساب کنیم، معادله گسترده (ضمنی) سهمی بدست می آید که به روش مربع کامل کردن قابل تبدیل به معادله استاندارد می شود.
مثال
با استاندارد کردن سهمی به معادله \({x^2} + 4y - 6x + 9 = 0\) مختصات راس و پارامتر سهمی را تعیین کنید.
\(\begin{array}{l}{x^2} + 4y - 6x + 9 = 0\\\\ \Rightarrow {x^2} - 6x + 9 = - 4y\\\\ \Rightarrow {\left( {x - 3} \right)^2} = - 4\left( {y - 0} \right)\\\\ \Rightarrow S\left[ {\begin{array}{*{20}{c}}3\\0\end{array}} \right]\;\;,\;\;4a = - 4 \Rightarrow a = - 1\end{array}\)
سهمی قائم و دهانه رو به پایین
ویژگی بازتابندگی سهمی ها
یکی از ویژگی های مهم سهمی این است که هر شعاع نوری از کانون آن به بدنه سهمی بتابد بازتاب آن موازی با محور سهمی باز خواهد گشت و برعکس هر شعاع نوری که موازی با محور سهمی به بدنه سهمی بتابد بازتاب آن از کانون سهمی خواهد گذشت، در واقع اگر خط d بر سهمی مماس و نقطه A نقطه تماس آن باشد، زاویه های \(\alpha \) و \(\beta \) برابرند.
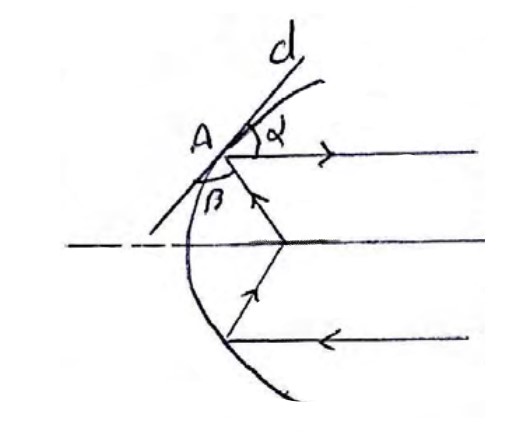
از این ویژگی در ساخت چراغ جلوی اتوموبیل ها استفاده می شود.
معادله یک سهمی به صورت \({y^2} - 2y + 8x + 9 = 0\) داده شده است، آن را به صورت استاندارد نوشته و کانون، خط هادی و مختصات راس و محور سهمی را مشخص کنید.
\(\begin{array}{l}{y^2} - 2y + 8x + 9 = 0\\\\ \Rightarrow {y^2} - 2y = - 8x - 9\\\\ \Rightarrow {y^2} - 2y + 1 = - 8x - 9 + 1\\\\ \Rightarrow {\left( {y - 1} \right)^2} = - 8\left( {x + 1} \right)\\\\S\left[ {\begin{array}{*{20}{c}}{ - 1}\\1\end{array}} \right]\;,\;4a = - 8 \Rightarrow a = - 2\;,\;F\left[ {\begin{array}{*{20}{c}}{ - 3}\\1\end{array}} \right]\\\\x = - 1 + 2 = 1\;\;,\;\;y = 1\end{array}\)
سهمی افقی، دهانه به سمت چپ
تهیه کننده: امیرحسین مطلبی



1736019749.png)















