درسنامه کامل هندسه دوازدهم فصل 3 بردارها
تعداد بازدید : 7.59Mخلاصه نکات هندسه دوازدهم فصل 3 بردارها - درسنامه شب امتحان هندسه دوازدهم فصل 3 بردارها - جزوه شب امتحان هندسه دوازدهم نوبت اول فصل 3 بردارها
فضای سه بعدی
فضای سه بعدی
منظور از فضای \({R^3}\) ، مجموعه تمام سه تایی های مرتبی مانند \(\left( {x,y,z} \right)\) است که در آنها x، y و z اعداد حقیقی باشند، به عبارت دیگر:
\({R^3} = \left\{ {\left( {x,y,z} \right)|x,y,z \in \mathbb{R}} \right\}\)
دستگاه قائم مختصات یا محور های مختصات دکارتی در فضا را به صورت \(O\left( {x,y,z} \right)\) نشان می دهند.
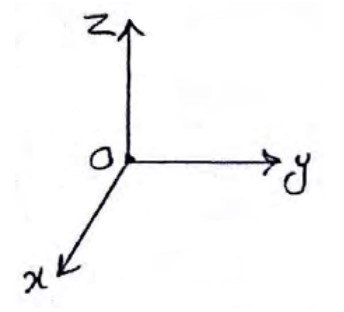
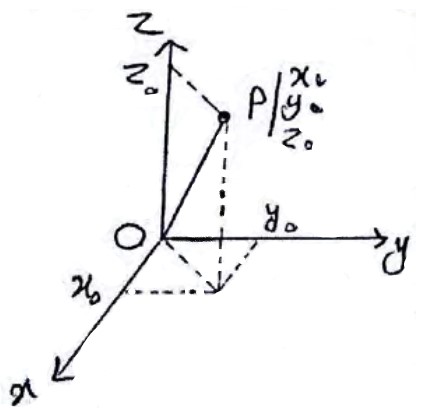
به طور کلی مختصات هر نقطه مانند P را در فضای \({R^3}\) به صورت \(P\left( {{x_0},{y_0},{z_0}} \right)\) مشخص می کنند که در آن \({x_0}\) طول نقطه P، \({y_0}\) عرض نقطه P و \({z_0}\) ارتفاع نقطه P نامیده می شود.
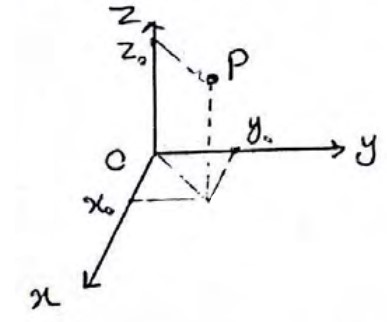
مثال
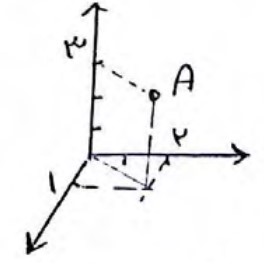
مختصات نقطه \(A\left( {1,2,3} \right)\) را در فضا مشخص کنید.
فرمول فاصله بین دو نقطه در فضا
اگر \(P\left( {{x_0},{y_0},{z_0}} \right)\) و \(Q\left( {{x_1},{y_1},{z_1}} \right)\) دو نقطه در فضا باشند، طول پاره خط PQ را با علامت \(\left| {PQ} \right|\) نشان داده و از رابطه زیر بدست می آوریم:
\(\left| {PQ} \right| = \sqrt {{{\left( {{x_0} - {x_1}} \right)}^2} + {{\left( {{y_0} - {y_1}} \right)}^2} + {{\left( {{z_0} - {z_1}} \right)}^2}} \)
مثال
اگر \(A\left( {2, - 3,1} \right)\) و \(B\left( {4,2,0} \right)\) دو نقطه در فضای \({R^3}\) باشد، طول AB را بیابید.
\(\begin{array}{l}\left| {AB} \right| = \sqrt {{{\left( {2 - 4} \right)}^2} + {{\left( { - 3 - 3} \right)}^2} + {{\left( {1 - 0} \right)}^2}} \\\\ \Rightarrow \left| {AB} \right| = \sqrt {30} \end{array}\)
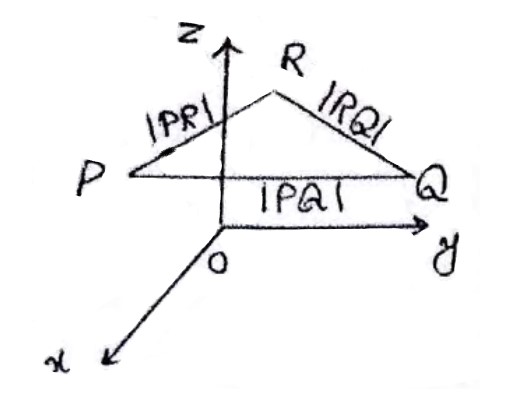
\(\left| {PQ} \right| = 0\) اگر و تنها اگر \(P = Q\)
\(\left| {PQ} \right| = \left| {QP} \right|\)
\(\left| {PQ} \right| \le \left| {PR} \right| + \left| {RQ} \right|\)
اگر \(A\left( {a,1, - 1} \right)\) و \(B\left( {2,a - 1,2a} \right)\) دو نقطه در فضا باشند، به ازای کدام مقادیر a، طول پاره خط AB برابر \(\sqrt {11} \) می باشد؟
\(\begin{array}{l}\left| {AB} \right| = \sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {1 - a - 1} \right)}^2} + {{\left( { - 1 - 2a} \right)}^2}} \\\\\sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {1 - a - 1} \right)}^2} + {{\left( { - 1 - 2a} \right)}^2}} = \sqrt {11} \\\\ \Rightarrow 6{a^2} - 4a - 2 = 0\\\\ \Rightarrow a = 1\;\;,\;\;a = - \frac{1}{3}\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
فاصله نقطه از مبدا مختصات
فاصله نقطه از مبدا مختصات
فاصله نقطه \(P\left( {{x_0},{y_0},{z_0}} \right)\) از مبدا مختصات \(O\left( {0,0,0} \right)\) یعنی طول پاره خط \(\left| {OP} \right|\) از رابطه زیر به دست می آید:
\(\left| {OP} \right| = \sqrt {x_0^2 + y_0^2 + z_0^2} \)
به ازای چه مقادیری از a فاصله نقطه \(P\left( {a + 1,3, - 1} \right)\) از مبدا مختصات برابر \(\sqrt {26} \) است؟
\(\begin{array}{l}\left| {OP} \right| = \sqrt {{{\left( {a + 1} \right)}^2} + {3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {26} \\\\ \Rightarrow \sqrt {{{\left( {a + 1} \right)}^2} + 10} = \sqrt {26} \\\\ \Rightarrow {\left( {a + 1} \right)^2} + 10 = 26 \Rightarrow {\left( {a + 1} \right)^2} = 16\\\\ \Rightarrow a + 1 = \pm 4 \Rightarrow a = 3\;\;,\;\;a = - 5\end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه دوازدهم
جزوه جامع هندسه دوازدهم فصل 1 ماتریس و کاربردها
جزوه جامع هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
جزوه جامع هندسه دوازدهم فصل 3 بردارها
مختصات نقطه وسط پاره خط
مختصات نقطه وسط پاره خط
اگر \(A\left( {{x_A},{y_A},{z_A}} \right)\) و \(B\left( {{x_B},{y_B},{z_B}} \right)\) دو نقطه دلخواه در فضای \({R^3}\) باشند، مختصات نقطه M وسط پاره خط AB از رابطه های زیر بدست می آید.
\(\begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2}\\\\{y_M} = \frac{{{y_A} + {y_B}}}{2}\\\\{z_M} = \frac{{{z_A} + {z_B}}}{2}\end{array}\)
نقاط \(A\left( {1,2,1} \right)\) و \(B\left( {3,1,4} \right)\) و \(C\left( {1,5,2} \right)\) سه راس مثلث \(\mathop {ABC}\limits^\Delta \) هستند. طول میانه AM را پیدا کنید.
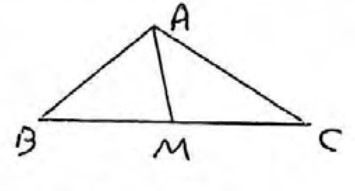
\(\begin{array}{l}{x_M} = \frac{{{x_B} + {x_C}}}{2} = \frac{{3 + 1}}{2} = 2\\\\{y_M} = \frac{{{y_B} + {y_C}}}{2} = \frac{{1 + 5}}{2} = 3\\\\{z_M} = \frac{{{z_B} + {z_C}}}{2} = \frac{{2 + 4}}{2} = 3\\\\M\left( {2,3,3} \right)\\\\\left| {AM} \right| = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 - 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 6 \end{array}\)
تهیه کننده: امیرحسین مطلبی
فرمول مختصات دو شکل در فضا
فرمول مختصات چهار راس متوازی الاضلاع در فضا
در متوازی الاضلاع ABCD رابطه های زیر بین مختصات چهار راس آن برقرار است:
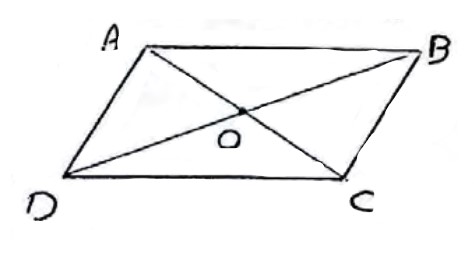
\(\begin{array}{l}{x_A} + {x_C} = {x_B} + {x_D}\\\\{y_A} + {y_C} = {y_B} + {y_D}\\\\{z_A} + {z_C} = {z_B} + {z_D}\end{array}\)
فرمول مختصات مرکز ثقل مثلث در فضای \({R^3}\)
در مثلث \(\mathop {ABC}\limits^\Delta \) نقطه برخورد سه میانه مثلث را مرکز ثقل مثلث نامیده و با G نامگذاری می کنیم، مختصات نقطه G از رابطه های زیر به دست می آید.
\(\begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3}\end{array}\)
1 اگر \(A\left( {1,2,1} \right)\) ، \(B\left( {3,1, - 1} \right)\) و \(C\left( {2,1,2} \right)\) مختصات سه راس متوازی الاضلاع ABCD باشند، مختصات O را بدست آورید.
\(\begin{array}{l}{x_A} + {x_C} = {x_B} + {x_D}\\\\ \Rightarrow 1 + 2 = 3 + {x_D} \Rightarrow {x_D} = 0\\\\{y_A} + {y_C} = {y_B} + {y_D}\\\\ \Rightarrow 2 + 1 = 1 + {y_D} \Rightarrow {y_D} = 2\\\\{z_A} + {z_C} = {z_B} + {z_D}\\\\ \Rightarrow 1 + 2 = - 1 + {z_D} \Rightarrow + {z_D} = 4\\\\D\left( {0,2,4} \right)\end{array}\)
2 نقاط \(A\left( {1,2, - 3} \right)\) و \(B\left( { - 2,1,1} \right)\) دو راس مثلث \(\mathop {ABC}\limits^\Delta \) هستند، اگر نقطه \(G\left( {1, - 3,4} \right)\) محل برخورد میانه های مثلث \(\mathop {ABC}\limits^\Delta \) باشند، مختصات راس C را بیابید.
\(\begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\\\ \Rightarrow 1 = \frac{{1 + \left( { - 2} \right) + {x_C}}}{3} \Rightarrow {x_C} = 4\\\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\\\ \Rightarrow - 3 = \frac{{2 + 1 + {y_C}}}{3} \Rightarrow {y_C} = - 12\\\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3}\\\\ \Rightarrow 4 = \frac{{ - 3 + 1 + {z_C}}}{3} \Rightarrow {z_C}\\\\C\left( {4, - 12,14} \right)\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
بردار در فضای سه بعدی
بردار در فضای سه بعدی
هر پاره خط جهت دار را یک بردار هندسی می نامند. برداری که نقطه ابتدای آن A و نقطه انتهای آن B باشد را به صورت \(\mathop {AB}\limits^ \to \) نشان می دهند.
هر بردار دارای سه مشخصه است:
- راستا
- جهت
- ندازه
مولفه های یک بردار
فرض کنید \(A\left( {{a_1},{a_2},{a_3}} \right)\) نقطه ای دلخواه در فضای \({R^3}\) باشد. پاره خط جهت دار با نقطه ی شروع مبدا \(O\left( {0,0,0} \right)\) و نقطه پایان \(A\left( {{a_1},{a_2},{a_3}} \right)\) را یک بردار در فضای \({R^3}\) می گوییم.
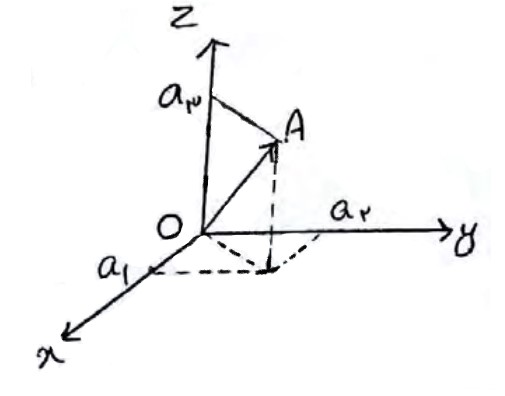
\(\mathop {OA}\limits^ \to = \left( {{a_1},{a_2},{a_3}} \right)\)
ویژگی های بردار در فضای \({R^3}\)
1) مختصات برداری که ابتدای آن نقطه \(A\left( {{x_1},{y_1},{z_1}} \right)\) و مختصات انتهای \(B\left( {{x_2},{y_2},{z_2}} \right)\) باشد عبارت است از:
\(\mathop {AB}\limits^ \to = \left( {{x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1}} \right)\)
2) برداری که ابتدا و انتهای آن یک نقطه باشد، بردار صفر نامیده می شود و آن را به صورت \(\mathop O\limits^ \to = \left( {0,0,0} \right)\) نشان می دهند.
3) تساوی دو بردار
دو بردار \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) و \(\mathop b\limits^ \to \left( {{b_1},{b_2},{b_3}} \right)\) مساوی هستند، اگر و تنها اگر مولفه های آنها نظیر به نظیر برابر باشند.
\(\begin{array}{l}\mathop a\limits^ \to = \mathop b\limits^ \to \Leftrightarrow \left( {{a_1},{a_2},{a_3}} \right) = \left( {{b_1},{b_2},{b_3}} \right)\\\\{a_1} = {b_1}\\\\{a_2} = {b_2}\\\\{a_3} = {b_3}\end{array}\)
مثال
مقادیر m و n را طوری بیابید که دو بردار \(\mathop a\limits^ \to \left( {2m,3, - 7} \right)\) و \(\mathop b\limits^ \to \left( {4,n - 1, - 7} \right)\) باهم مساوی باشند.
\(\begin{array}{l}2m = 4 \Rightarrow m = 2\\\\n - 1 = 3 \Rightarrow n = 4\end{array}\)
4) اندازه (طول) یک بردار
طول یا اندازه بردار \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) را با علامت \(\left| a \right|\) نشان داده و از فرمول زیر محاسبه می کنیم:
\(|\mathop a\limits^ \to | = \sqrt {a_1^2 + a_2^2 + a_3^2} \)
مثال
طول بردار \(\mathop a\limits^ \to \left( { - 3,0,4} \right)\) را بیابید.
\(|\mathop a\limits^ \to | = \sqrt {{{\left( { - 3} \right)}^2} + {0^2} + {4^2}} = \sqrt {9 + 16} = 5\)
5) زاویه بین دو بردار غیر صفر \(\mathop a\limits^ \to \) و \(\mathop b\limits^ \to \) را زاویه ای مانند \(\theta \) در نظر می گیریم که:
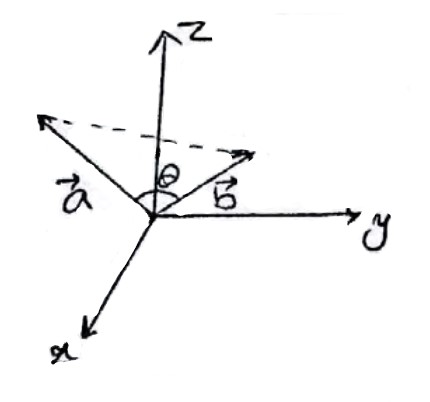
\(0 \le \theta \le \pi \)
6) ضرب عدد در بردار
اگر m یک عدد حقیقی و \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) یک بردار باشد، حاصل ضرب m در بردار a به صورت زیر تعریف می کنیم:
\(m\mathop a\limits^ \to \left( {m{a_1},m{a_2},m{a_3}} \right)\)
7) قرینه بردار
اگر \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) یک بردار باشد قرینه \(\mathop a\limits^ \to \) را با علامت \( - \mathop a\limits^ \to \) نشان داده و به صورت زیر تعریف می کنیم:
\( - \mathop a\limits^ \to \left( { - {a_1}, - {a_2}, - {a_3}} \right)\)
8) جمع بردار ها
اگر \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) و \(\mathop b\limits^ \to \left( {{b_1},{b_2},{b_3}} \right)\) دو بردار باشند، مجموع آنها را با علامت \(\mathop a\limits^ \to + \mathop b\limits^ \to \) نشان داده و به صورت زیر تعریف می کنیم:
\(\begin{array}{l}\mathop a\limits^ \to + \mathop b\limits^ \to = \left( {{a_1},{a_2},{a_3}} \right) + \left( {{b_1},{b_2},{b_3}} \right)\\\\ \Rightarrow \left( {{a_1} + {b_1},{a_2} + {b_2},{a_3} + {b_3}} \right)\end{array}\)
به همین ترتیب داریم:
\(\begin{array}{l}\mathop a\limits^ \to - \mathop b\limits^ \to = \left( {{a_1},{a_2},{a_3}} \right) - \left( {{b_1},{b_2},{b_3}} \right)\\\\ \Rightarrow \left( {{a_1} - {b_1},{a_2} - {b_2},{a_3} - {b_3}} \right)\end{array}\)
بردار های \(\mathop a\limits^ \to \left( {2, - 1,3} \right)\) ، \(\mathop b\limits^ \to \left( { - 1,3, - 2} \right)\) و \(\mathop c\limits^ \to \left( {2,4,1} \right)\) مفروض است بردار \(2a + b - c\) را بدست آورده، سپس طول آن را بیابید.
\(\begin{array}{l}2a + b - c\\\\ \Rightarrow 2\left( {2, - 1,3} \right) + \left( { - 1,3, - 2} \right) - \left( {2,4,1} \right)\\\\ \Rightarrow \left( {1, - 3,3} \right)\\\\\left| {2a + b - c} \right| = \sqrt {{1^2} + {{\left( { - 3} \right)}^2} + {3^2}} = \sqrt {19} \end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه دوازدهم
جزوه جامع هندسه دوازدهم فصل 1 ماتریس و کاربردها
جزوه جامع هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
جزوه جامع هندسه دوازدهم فصل 3 بردارها
دو بردار هم راستا
دو بردار هم راستا
دو بردار \(\mathop a\limits^ \to \) و \(\mathop b\limits^ \to \) را هم راستا می گویند هر گاه یکی مضربی از دیگری باشد، به عبارت دیگر:
\(\mathop b\limits^ \to = r\mathop a\limits^ \to \)
خواص جمع بردار ها
اگر \(\mathop a\limits^ \to \)، \(\mathop b\limits^ \to \) و \(\mathop c\limits^ \to \) سه بردار دلخواه و \(\mathop O\limits^ \to = \left( {0,0,0} \right)\) بردار صفر و نیز r و S دو عدد حقیقی باشند؛ آنگاه:
1) خاصیت جا به جایی جمع
\(\mathop a\limits^ \to + \mathop b\limits^ \to = \mathop b\limits^ \to + \mathop a\limits^ \to \)
2) خاصیت شرکت پذیری جمع
\(\mathop a\limits^ \to + (\mathop b\limits^ \to + \mathop c\limits^ \to ) = (\mathop b\limits^ \to + \mathop a\limits^ \to ) + \mathop c\limits^ \to \)
3) عضو قرینه
\(\mathop a\limits^ \to + (\mathop { - a}\limits^ \to ) = ( - \mathop a\limits^ \to ) + \mathop a\limits^ \to = \mathop O\limits^ \to \)
4) عضو خنثی
\(\mathop a\limits^ \to + \mathop O\limits^ \to = \mathop O\limits^ \to + \mathop a\limits^ \to = \mathop a\limits^ \to \)
5) \(r(\mathop a\limits^ \to + \mathop b\limits^ \to ) = r\mathop a\limits^ \to + \mathop {rb}\limits^ \to \)
6) \((r + S)\mathop a\limits^ \to = r\mathop a\limits^ \to + S\mathop a\limits^ \to \)
7) \((rS)\mathop a\limits^ \to = \mathop r\limits^ \to (S\mathop a\limits^ \to )\)
8) \(|\mathop b\limits^ \to | = |r| \times |\mathop a\limits^ \to |\; \Rightarrow \;\mathop b\limits^ \to = r\mathop a\limits^ \to \)
بردار های یکه محور های مختصات در فضای \({R^3}\)
هر بردار که طول و اندازه آن یک واحد باشد، بردار یکه نامیده می شود. بردار یکه در جهت محور طول ها را با \(\mathop i\limits^ \to = \left( {1,0,0} \right)\) و بردار یکه در جهت عرض ها را با \(\mathop j\limits^ \to = \left( {0,1,0} \right)\) و بردار یکه در جهت محور ارتفاع ها را با \(\mathop k\limits^ \to = \left( {0,0,1} \right)\) نشان می دهیم؛ هر بردار مانند \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) را می توان بر حسب بردار های یکه \(\mathop i\limits^ \to \)، \(\mathop j\limits^ \to \) و \(\mathop k\limits^ \to \) نوشت:
\(\begin{array}{l}\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\\\\\left( {{a_1},{a_2},{a_3}} \right) = \left( {{a_1},0,0} \right) + \left( {0,{a_2},0} \right) + \left( {0,0,{a_3}} \right)\\\\ \Rightarrow {a_1}\left( {1,0,0} \right) + {a_2}\left( {0,1,0} \right) + {a_3}\left( {0,0,1} \right)\\\\ \Rightarrow {a_1}\mathop i\limits^ \to + {a_2}\mathop j\limits^ \to + {a_3}\mathop k\limits^ \to \\\\ \Rightarrow a = \left( {{a_1},{a_2},{a_3}} \right) = {a_1}\mathop i\limits^ \to + {a_2}\mathop j\limits^ \to + {a_3}\mathop k\limits^ \to \end{array}\)
اگر \(\mathop a\limits^ \to = 3\mathop i\limits^ \to - 2\mathop j\limits^ \to - \mathop k\limits^ \to \) و \(\mathop b\limits^ \to = \left( {3,1, - 1} \right)\) و \(r = 2\) باشد، بردار \(r\mathop b\limits^ \to - \mathop a\limits^ \to \) را بدست آورید.
\(\begin{array}{l}\mathop a\limits^ \to = 3\mathop i\limits^ \to - 2\mathop j\limits^ \to - \mathop k\limits^ \to = \left( {3,2, - 1} \right)\\\\r\mathop b\limits^ \to - \mathop a\limits^ \to = 2\mathop b\limits^ \to - \mathop a\limits^ \to \\\\ \Rightarrow 2\left( {3,1, - 1} \right) - \left( {3,2, - 1} \right)\\\\ \Rightarrow \left( {6,2, - 2} \right) - \left( {3,2, - 1} \right) = \left( {3,0, - 1} \right)\end{array}\)
تهیه کننده: امیرحسین مطلبی
ضرب داخلی دو بردار
ضرب داخلی دو بردار
1) اگر \(\mathop a\limits^ \to \) و \(\mathop b\limits^ \to \) دو بردار غیر صفر و زاویه بین آنها \(\left( {0 \le \theta \le 1} \right)\;\;\theta \) باشد، در این صورت ضرب داخلی \(\mathop a\limits^ \to \) در \(\mathop b\limits^ \to \) با علامت \(\mathop a\limits^ \to \times \mathop b\limits^ \to \) نشان داده و به صورت زیر تعریف می کنیم:
\(\mathop a\limits^ \to \times \mathop b\limits^ \to = \left| a \right|\left| b \right|\cos \theta \)
2) اگر \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) و \(\mathop b\limits^ \to \left( {{b_1},{b_2},{b_3}} \right)\) دو بردار در فضای \({R^3}\) باشند، در این صورت ضرب داخلی \(\mathop a\limits^ \to \) در \(\mathop b\limits^ \to \) را با علامت \(\mathop a\limits^ \to \times \mathop b\limits^ \to \) نشان داده و به صورت زیر تعریف می کنیم:
\(\mathop a\limits^ \to \times \mathop b\limits^ \to = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\)
مثال
زاویه بین دو بردار \(\mathop a\limits^ \to \left( {2,2,2} \right)\) و \(\mathop b\limits^ \to \left( {2,0, - 2} \right)\) را بیابید.
\(\begin{array}{l}\left| a \right| = \sqrt {{2^2} + {2^2} + {2^2}} = \sqrt {12} \\\\\left| b \right| = \sqrt {{2^2} + {0^2}{{\left( { - 2} \right)}^2}} = \sqrt {18} \\\\\mathop a\limits^ \to \times \mathop b\limits^ \to = 2 \times 2 + 0 \times 2 + 2 \times \left( { - 2} \right) = 0\\\\\mathop a\limits^ \to \times \mathop b\limits^ \to = \left| a \right|\left| b \right|\cos \theta \Rightarrow \sqrt {12} \times \sqrt 8 \cos \theta \\\\ \Rightarrow \cos \theta = 0 \Rightarrow \theta = {90^0}\end{array}\)
خواص ضرب داخلی
1) چون حاصل ضرب داخلی دو بردار یک عدد حقیقی است به آن ضرب اسکالر یا ضرب عددی نیز می گویند.
2) اگر یکی از دو بردار a یا b یا هر دو برابر بردار صفر باشند، حاصل ضرب داخلی آنها صفر می باشد.
\(\mathop a\limits^ \to = \mathop 0\limits^ \to \; \vee \;\mathop b\limits^ \to = \mathop 0\limits^ \to \; \Rightarrow \;\mathop a\limits^ \to \times \mathop b\limits^ \to = 0\)
عکس رابطه درست نیست.
3) ضرب داخلی دو بردار خاصیت جا به جایی دارد.
\(\mathop a\limits^ \to \times \mathop b\limits^ \to = \mathop b\limits^ \to \times \mathop a\limits^ \to \)
4) برای هر دو بردار a و b و هر عدد حقیقی m داریم:
\(m\mathop a\limits^ \to \times \mathop b\limits^ \to = \mathop a\limits^ \to \times m\mathop b\limits^ \to = m(\mathop a\limits^ \to \times \mathop b\limits^ \to )\)
5) حاصل ضرب داخلی هر بردار در خودش برابر است با مجذور اندازه آن بردار:
\(\mathop a\limits^ \to \times \mathop a\limits^ \to = \left| a \right|\left| a \right|\cos 0 = {\left| a \right|^2}\)
6) اگر دو بردار بر هم عمود باشند، حاصل ضرب داخلی آنها صفر است و بر عکس:
\(\mathop a\limits^ \to \bot \mathop b\limits^ \to \Leftrightarrow \mathop b\limits^ \to \times \mathop a\limits^ \to = 0\)
7) ضرب داخلی بر روی جمع بردار ها، خاصیت توزیع پذیری (پخش) دارد.
\(\begin{array}{l}\mathop a\limits^ \to \times (\mathop b\limits^ \to + \mathop c\limits^ \to ) = \mathop a\limits^ \to \times \mathop b\limits^ \to + \mathop a\limits^ \to \times \mathop c\limits^ \to \\\\\mathop {(a}\limits^ \to + \mathop b\limits^ \to ) \times \mathop c\limits^ \to = \mathop a\limits^ \to \times \mathop c\limits^ \to + \mathop b\limits^ \to \times \mathop c\limits^ \to \end{array}\)
تصویر قائم یک بردار روی بردار دیگر
دو بردار غیر صفر \(\mathop a\limits^ \to \) و \(\mathop b\limits^ \to \) را که زاویه بین آنها \(\theta \) است در نظر می گیریم. تصویر قائم بردار \(\mathop a\limits^ \to \) روی بردار \(\mathop b\limits^ \to \) را با بردار \(\;\mathop {a'}\limits^ \to \;\) نشان داده و از فرمول زیر محاسبه می کنیم:
\(\;\mathop {a'}\limits^ \to \; = \frac{{\;\mathop a\limits^ \to \; \times \;\mathop b\limits^ \to \;}}{{|b{|^2}}}\; \times \mathop b\limits^ \to \;\)
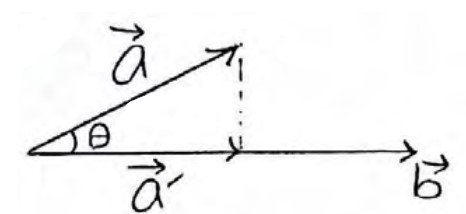
تصویر قائم بردار \(\mathop a\limits^ \to \left( {2,3, - 2} \right)\) را بر روی امتداد بردار \(\mathop b\limits^ \to \left( { - 1,2, - 2} \right)\) بیابید.
\(\begin{array}{l}\;\mathop a\limits^ \to \; \times \;\mathop b\limits^ \to \; = - 2 + 6 + 4 = 8\\\\|\;\;\mathop b\limits^ \to \;| = \sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {{\left( { - 2} \right)}^2}} = \sqrt 9 = 3\\\\\mathop {a'}\limits^ \to \; = \frac{{\;\mathop a\limits^ \to \; \times \;\mathop b\limits^ \to \;}}{{|b{|^2}}}\; \times \mathop b\limits^ \to \; = \frac{8}{9}\left( { - 1,2, - 2} \right)\\\\ \Rightarrow \mathop {a'}\limits^ \to \; = ( - \frac{8}{9},\frac{{16}}{9}, - \frac{{16}}{9})\end{array}\)
تهیه کننده: امیرحسین مطلبی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
ضرب خارجی
ضرب خارجی
فرض کنیم \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) و \(\mathop b\limits^ \to \left( {{b_1},{b_2},{b_3}} \right)\) دو بردار باشند، ضرب خارجی \(\mathop a\limits^ \to \) در \(\mathop b\limits^ \to \) را با علامت \(\mathop a\limits^ \to \times \mathop b\limits^ \to \) نشان داده و به صورت زیر تعریف می کنیم:
\(\begin{array}{l}\mathop a\limits^ \to \times \mathop b\limits^ \to = \left| {\begin{array}{*{20}{c}}i&j&k\\{{a_1}}&{{a_2}}&{{a_3}}\\{{b_1}}&{{b_2}}&{{b_3}}\end{array}} \right|\\\\\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|\mathop i\limits^ \to - \left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_3}}\\{{b_1}}&{{b_3}}\end{array}} \right|\mathop j\limits^ \to + \left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|\mathop k\limits^ \to \\\\\left( {{a_2}{b_3} - {a_3}{b_2}, - {a_1}{b_3} + {a_3}{b_1},{a_1}{b_2} - {a_2}{b_1}} \right)\end{array}\)
از نظر هندسی
ضرب خارجی دو بردار بر هر دو بردار \(\mathop a\limits^ \to \) و \(\mathop b\limits^ \to \) و صفحه تشکیل دهنده از دو بردار \(\mathop a\limits^ \to \) و \(\mathop b\limits^ \to \)، عمود است.
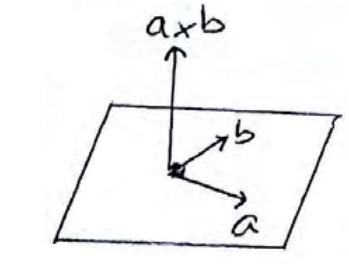
مثال
اگر \(\mathop a\limits^ \to \left( {1,2, - 1} \right)\) و \(\mathop b\limits^ \to \left( {0,1,2} \right)\) مطلوب است، محاسبه: \(\mathop a\limits^ \to \times \mathop b\limits^ \to \)
\(\begin{array}{l}\mathop a\limits^ \to \times \mathop b\limits^ \to = \left| {\begin{array}{*{20}{c}}i&j&k\\1&2&{ - 1}\\0&1&2\end{array}} \right|\\\\\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&2\end{array}} \right|\mathop i\limits^ \to - \left| {\begin{array}{*{20}{c}}1&{ - 1}\\0&2\end{array}} \right|\mathop j\limits^ \to + \left| {\begin{array}{*{20}{c}}1&2\\0&1\end{array}} \right|\mathop k\limits^ \to \\\\ \Rightarrow \mathop a\limits^ \to \times \mathop b\limits^ \to = \left( {5, - 2,1} \right)\end{array}\)
حاصل ضرب خارجی بردار های یکه
\(\begin{array}{l}\mathop i\limits^ \to \times \mathop j\limits^ \to = \mathop k\limits^ \to \;\;\;\;,\;\;\;\;\mathop j\limits^ \to \times \mathop i\limits^ \to = - \mathop k\limits^ \to \\\\\mathop j\limits^ \to \times \mathop k\limits^ \to = \mathop i\limits^ \to \;\;\;\;,\;\;\;\;\mathop k\limits^ \to \times \mathop j\limits^ \to = - \mathop i\limits^ \to \\\\\mathop k\limits^ \to \times \mathop i\limits^ \to = \mathop j\limits^ \to \;\;\;\;,\;\;\;\;\mathop i\limits^ \to \times \mathop k\limits^ \to = - \mathop j\limits^ \to \end{array}\)
مثال
حاصل عبارت های زیر را بدست آورید.
الف) \(\mathop i\limits^ \to \times (\mathop j\limits^ \to \times \mathop k\limits^ \to ) = \)
\(\mathop i\limits^ \to \times (\mathop j\limits^ \to \times \mathop k\limits^ \to ) = \mathop i\limits^ \to \times ( - \mathop j\limits^ \to ) = - \mathop i\limits^ \to \times \mathop j\limits^ \to = - \mathop k\limits^ \to \)
ب) \((\mathop j\limits^ \to \times \mathop k\limits^ \to ) \times \mathop k\limits^ \to = \)
\((\mathop j\limits^ \to \times \mathop k\limits^ \to ) \times \mathop k\limits^ \to = \mathop i\limits^ \to \times \mathop k\limits^ \to = - \mathop j\limits^ \to \)
ویژگی های ضرب خارجی
1) ضرب خارجی دو بردار خاصیت جا به جایی ندارد ولی:
\(\mathop a\limits^ \to \times \mathop b\limits^ \to = - \mathop b\limits^ \to \times \mathop a\limits^ \to \)
2) ضرب خارجی هر بردار در خودش برابر بردار صفر است.
\(\mathop a\limits^ \to \times \mathop a\limits^ \to = \mathop 0\limits^ \to \)
اثبات:
\(\begin{array}{l}\mathop a\limits^ \to \times \mathop a\limits^ \to = - \mathop a\limits^ \to \times \mathop a\limits^ \to \Rightarrow \mathop a\limits^ \to \times \mathop a\limits^ \to + \mathop a\limits^ \to \times \mathop a\limits^ \to = 0\\\\ \Rightarrow 2(\mathop a\limits^ \to \times \mathop a\limits^ \to ) = 0 \Rightarrow \mathop a\limits^ \to \times \mathop a\limits^ \to = \mathop 0\limits^ \to \\\\\mathop i\limits^ \to \times \mathop i\limits^ \to = \mathop j\limits^ \to \times \mathop j\limits^ \to = \mathop k\limits^ \to \times \mathop k\limits^ \to = \mathop 0\limits^ \to \end{array}\)
3) ضرب خارجی هر بردار در بردار صفر، برابر بردار صفر است.
\(\mathop a\limits^ \to \times \mathop 0\limits^ \to = \mathop 0\limits^ \to \)
4) برای هر دو بردار \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) و هر عدد حقیقی m داریم:
\(m\mathop a\limits^ \to \times \mathop b\limits^ \to = \mathop a\limits^ \to \times m\mathop b\limits^ \to = m(\mathop a\limits^ \to \times \mathop b\limits^ \to )\)
5) ضرب داخلی بردار ها نسبت به جمع بردار ها، خاصیت توزیع پذیری دارد:
\(\begin{array}{l}\mathop a\limits^ \to \times (\mathop b\limits^ \to + \mathop c\limits^ \to ) = \mathop a\limits^ \to \times \mathop b\limits^ \to + \mathop a\limits^ \to \times \mathop c\limits^ \to \\\\(\mathop a\limits^ \to + \mathop b\limits^ \to ) \times \mathop c\limits^ \to = \mathop a\limits^ \to \times \mathop c\limits^ \to + \mathop b\limits^ \to \times \mathop c\limits^ \to \end{array}\)
6) ضرب خارجی بردار ها خاصیت شرکت پذیری ندارد:
\(\mathop a\limits^ \to \times (\mathop b\limits^ \to \times \mathop c\limits^ \to ) \ne (\mathop a\limits^ \to \times \mathop b\limits^ \to ) \times \mathop c\limits^ \to \)
7) فرض کنیم \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) دو بردار دلخواه باشند، در این صورت:
\(\begin{array}{l}\mathop a\limits^ \to \times (\mathop a\limits^ \to \times \mathop b\limits^ \to ) = 0\\\\\mathop b\limits^ \to \times (\mathop a\limits^ \to \times \mathop b\limits^ \to ) = 0\end{array}\)
اثبات:
فرض کنیم \(\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\) و \(\mathop b\limits^ \to \left( {{b_1},{b_2},{b_3}} \right)\) در نتیجه:
\(\begin{array}{l}\mathop a\limits^ \to \times (\mathop a\limits^ \to \times \mathop b\limits^ \to ) = 0\\\\\mathop a\limits^ \to \left( {{a_1},{a_2},{a_3}} \right)\\\\\mathop b\limits^ \to \left( {{b_1},{b_2},{b_3}} \right)\\\\{a_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {a_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {a_3}\left( {{a_1}{b_1} - {a_2}{b_1}} \right) = 0\end{array}\)
8) برای هر دو بردار غیر صفر a و b که زاویه بین آنها \(\theta \) باشد، داریم:
\(|\mathop a\limits^ \to \times \mathop b\limits^ \to | = |\mathop a\limits^ \to | \times |\mathop b\limits^ \to |\sin \theta \)
9) برای هر دو بردار غیر صفر \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) ، بردار \(\mathop a\limits^ \to \) با \(\mathop b\limits^ \to \) موازی است، اگر و فقط اگر:
\(|\mathop a\limits^ \to \times \mathop b\limits^ \to | = 0\;\; \vee \;\;\mathop a\limits^ \to \times \mathop b\limits^ \to = \mathop 0\limits^ \to \)
اثبات:
\(\begin{array}{l}\mathop a\limits^ \to \times \mathop b\limits^ \to = \mathop 0\limits^ \to \Leftrightarrow |\mathop a\limits^ \to \times \mathop b\limits^ \to | = 0\\\\|\mathop a\limits^ \to \times \mathop b\limits^ \to | = 0 \Leftrightarrow \left| a \right|\left| b \right|\sin \theta = 0\\\\\left| a \right|\left| b \right|\sin \theta = 0 \Leftrightarrow \sin \theta = 0 \Leftrightarrow \theta = 0\\\\\theta = 0 \Leftrightarrow a\parallel b\end{array}\)
بردار های \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) مفروض اند، به طوری که \(|\mathop a\limits^ \to \times \mathop b\limits^ \to | = 72\;,\;|\mathop b\limits^ \to | = 26\;,\;|\mathop a\limits^ \to | = 3\) مقدار \(\mathop a\limits^ \to \times \mathop b\limits^ \to \) را محاسبه کنید.
\(\begin{array}{l}|\mathop a\limits^ \to \times \mathop b\limits^ \to | = |\mathop a\limits^ \to | \times |\mathop b\limits^ \to |\sin \theta \\\\ \Rightarrow 72 = 3 \times 26\sin \theta \Rightarrow \sin \theta = \frac{{12}}{{13}}\\\\\cos \theta = \sqrt {1 - \sin {\theta ^2}} = \sqrt {1 - {{(\frac{{12}}{{13}})}^2}} = \sqrt {\frac{{25}}{{169}}} \\\\ \Rightarrow \cos \theta = \pm \frac{5}{{13}}\\\\\mathop a\limits^ \to \times \mathop b\limits^ \to = |\mathop a\limits^ \to | \times |\mathop b\limits^ \to |\cos \theta = 3 \times 26 \times ( \pm \frac{5}{{13}})\\\\ \Rightarrow \mathop a\limits^ \to \times \mathop b\limits^ \to = \pm 30\end{array}\)
تهیه کننده: امیرحسین مطلبی
جزوات جامع پایه دوازدهم
جزوه جامع هندسه دوازدهم فصل 1 ماتریس و کاربردها
جزوه جامع هندسه دوازدهم فصل 2 آشنایی با مقاطع مخروطی
جزوه جامع هندسه دوازدهم فصل 3 بردارها
مساحت ساخته شده دو بردار
مساحت ساخته شده دو بردار
مساحت متوازی الاضلاع ساخته شده روی دو بردار
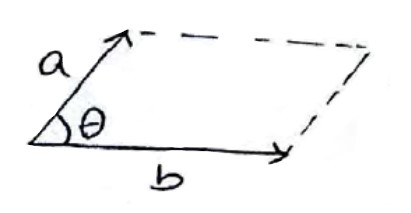
اگر \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) دو بردار غیر صفر باشند، که زاویه بین آنها \(\theta \) باشد، مساحت متوازی الاضلاعی که توسط دو بردار ساخته می شود و \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) دو ضلع مجاور آن هستند برابر است با اندازه حاصل ضرب خارجی دو بردار \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) :
\(S = |\mathop a\limits^ \to \times \mathop b\limits^ \to |\)
مثال
مساحت متوازی الاضلاعی که توسط بردار های \(\mathop a\limits^ \to \left( { - 1,0,1} \right)\) و \(\mathop b\limits^ \to \left( {0,1,1} \right)\) تولید می شود را بدست آورید.
\(\begin{array}{l}\mathop a\limits^ \to \times \mathop b\limits^ \to = \left( { - 1, - 1, - 1} \right)\\\\S = |\mathop a\limits^ \to \times \mathop b\limits^ \to | = \sqrt {1 + 1 + 1} = \sqrt 3 \end{array}\)
مساحت مثلث
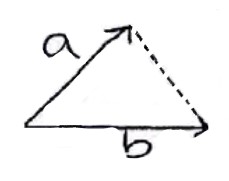
مساحت مثلثی که به وسیله دو بردار \(\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) ساخته می شود برابر است با:
\(S = \frac{1}{2}|\mathop a\limits^ \to \times \mathop b\limits^ \to |\)
مثال
مساحت مثلث \(\mathop {ABC}\limits^\Delta \) به رئوس \(A = \left( {1,2,0} \right)\) ، \(B = \left( {3,0, - 3} \right)\) و \(C = \left( {5,2,6} \right)\) را بیابید.
\(\begin{array}{l}\mathop {AB}\limits^ \to = \left( {3 - 1,0 - 2, - 3 - 0} \right) = \left( {2, - 2, - 3} \right)\\\\\mathop {AC}\limits^ \to = \left( {5 - 1,2 - 2,6 - 0} \right) = \left( {4,0,6} \right)\\\\\mathop {AB}\limits^ \to \times \mathop {AC}\limits^ \to = \left( { - 12, - 24,8} \right)\\\\S = \frac{1}{2}|\mathop {AB}\limits^ \to \times \mathop {AC}\limits^ \to | = \frac{1}{2}\sqrt {144 + 576 + 64} \\\\ \Rightarrow \frac{1}{2}\sqrt {784} = \frac{1}{2} \times 28 = 14\end{array}\)
حجم متوازی السطوح
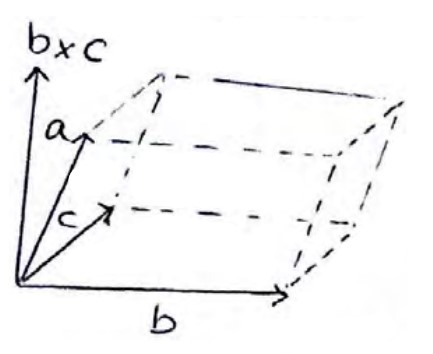
اگر \(\mathop c\limits^ \to \;,\;\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) سه بردار باشند که در یک صفحه نباشند، حجم متوازی السطوحی که روی این سه بردار ساخته می شود، به طوری که سه بردار یال های مجاور آن باشند از رابطه زیر محاسبه می شود:
\(V = |\mathop a\limits^ \to .(\mathop b\limits^ \to \times \mathop c\limits^ \to )| = |\mathop b\limits^ \to .(\mathop c\limits^ \to \times \mathop a\limits^ \to )| = |\mathop c\limits^ \to .(\mathop a\limits^ \to \times \mathop b\limits^ \to )|\)
مثال
حجم متوازی السطوحی را بدست آورید که توسط بردار های \(\mathop a\limits^ \to = \left( {1,1,0} \right)\) ، \(\mathop b\limits^ \to = \left( {0,1,1} \right)\) و \(\mathop c\limits^ \to = \left( {1,0,1} \right)\) تولید می شود.
\(\begin{array}{l}\mathop b\limits^ \to \times \mathop c\limits^ \to = \left( {1,1, - 1} \right)\\\\V = |\mathop a\limits^ \to .(\mathop b\limits^ \to \times \mathop c\limits^ \to )| = |1 + 1 + 0| = 2\end{array}\)
سه بردار هم صفحه
سه بردار \(\mathop c\limits^ \to \;,\;\mathop b\limits^ \to \;,\;\mathop a\limits^ \to \) را هم صفحه گویند هرگاه:
\(\mathop a\limits^ \to \times (\mathop b\limits^ \to \times \mathop c\limits^ \to ) = 0\)
1 مساحت مثلثی که رئوس آن با نقاط \(A = \left( {3,5,7} \right)\) ، \(B = \left( {5,5,0} \right)\) و \(C = \left( { - 4,0,4} \right)\) داده شده را بیابید.
\(\begin{array}{l}\mathop {AB}\limits^ \to = \left( {2,0, - 7} \right)\\\\\mathop {AC}\limits^ \to = \left( { - 7, - 5, - 3} \right)\\\\\mathop {AB\;}\limits^ \to \times \;\mathop {AC}\limits^ \to = \left( { - 35,55, - 10} \right)\\\\|\mathop {AB\;}\limits^ \to \times \;\mathop {AC}\limits^ \to | = \sqrt {{{\left( { - 35} \right)}^2} + {{55}^2} + {{\left( { - 10} \right)}^2}} \\\\ \Rightarrow |\mathop {AB\;}\limits^ \to \times \;\mathop {AC}\limits^ \to | = \sqrt {4350} \\\\S = \frac{1}{2}|\mathop {AB\;}\limits^ \to \times \;\mathop {AC}\limits^ \to | = \frac{1}{2}\sqrt {4350} \end{array}\)
2 ثابت کنید سه بردار \(\mathop c\limits^ \to = \left( {3, - 4,7} \right)\;,\;\mathop b\limits^ \to = \left( {1,2, - 3} \right)\;,\;\mathop a\limits^ \to = \left( {2, - 1,2} \right)\) هم صفحه اند.
\(\begin{array}{l}\mathop b\limits^ \to \times \mathop c\limits^ \to = \left( {2, - 16, - 10} \right)\\\\\mathop a\limits^ \to \; \times \;(\mathop b\limits^ \to \; \times \;\mathop c\limits^ \to ) = \left( {2, - 1,2} \right) \times \left( {2, - 16, - 10} \right)\\\\ \Rightarrow \mathop a\limits^ \to \; \times \;(\mathop b\limits^ \to \; \times \;\mathop c\limits^ \to ) = 4 + 16 - 20 = 0\end{array}\)
تهیه کننده: امیرحسین مطلبی



1736019749.png)















