درسنامه کامل ریاضی نهم فصل 1 مجموعه ها
تعداد بازدید : 7.59Mخلاصه نکات ریاضی نهم فصل 1 مجموعه ها - درسنامه شب امتحان ریاضی نهم فصل 1 مجموعه ها - جزوه شب امتحان ریاضی نهم نوبت اول فصل 1 مجموعه ها
مجموعه
مجموعه
به دسته ای از اشیاء کاملا مشخص و دو به دو متمایز (غیر تکراری) «مجموعه» می گویند.
مثال
کدام یک از عبارات زیر مشخص کننده یک مجموعه است؟
الف) 3 عدد زوج متوالی
مجموعه نیست
ب) 4 گل زیبا
مجموعه نیست
پ) اعداد اول کمتر از 10
مجموعه است
1 جموعه را به صورت آکولاد { } نشان می دهند و مجموعه را با حروف بزرگ انگلیسی نام گذاری می کنند.
2 به هر یک از اعداد و عبارت داخل مجموعه عضو می گویند و علامت عضو بودن به صورت \( \in \)و علامت عضو نبودن به صورت \( \notin \)می باشد.
3 تعداد عضو های هر مجموعه مانند A را به صورت n(A) نشان می دهند.
مثال
با توجه به مجموعه ی A درستی یا نادرستی هر عبارت را مشخص کنید.
\(A = \{ 3\,,\,\{ 4\,,\,5\} \,,\,6\} \)
\(n(A) = 4\)
نادرست
\(3 \in A\)
درست
\(4 \notin A\)
درست
\(\{ 6\} \in A\)
نادرست
تهیه کننده : مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
مجموعه تهی
مجموعه تهی
مجموعه ای که دارای هیچ عضوی نباشد. علامت مجموعه تهی بصورت { } یا \(\emptyset \) می باشد.
مثال
کدام یک از مجموعه های زیر مجموعه تهی است؟
الف اعداد طبیعی کمتر از 4
\(\{ 1\,,\,2\,,\,3\} \)
ب عداد صحیح کمتر از صفر
\(\{ \ldots \,,\, - 3\,,\, - 2\,,\, - 1\} \)
پ اعداد طبیعی بین 4 و 5
\(\{ \} \)
مجموعه تهی است
تهیه کننده : مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
دو مجموعه برابر
دو مجموعه برابر
دو مجموعه A و B را برابر می گویند که هر عضو مجموعه A در مجموعه B و هر عضو مجموعه B در مجموعه A وجود داشته باشد؛ مانند دو مجموعه ی مقابل:
\(B = \left\{ {\sqrt 9 ,7,\frac{{20}}{5}} \right\}\) و \(A = \{ 4,3,7\} \)
مثال
دو مجموعه ی زیر برابرند،مقدار x و y را به دست آورید؟
\(\left\{ {x - 7,3} \right\} = \left\{ {4,y} \right\}\)
\(\left\{ \begin{array}{l}x - 7 = 4 \Rightarrow x = 11\\\\y = 3\end{array} \right.\)
تهیه کننده : مسعود زیرکاری
زیر مجموعه
زیر مجموعه
مجموعه A زیر مجموعه B است. هر گاه هر عضو مجموعه A عضوی از مجموعه B باشد و آن را به صورت \(A \subseteq B\) نشان می دهد. اگر A زیر مجموعه B نباشد آن را بصورت \(A \not\subset B\) نشان می دهند.
1 اگر \(A \subseteq B\) باشد آنگاه رابطه های زیر همواره برقرار است:
\(\left\{ \begin{array}{l}A \cup B = B\\\\A \cap B = A\end{array} \right.\)
2 برای پیدا کردن تعداد زیر مجموعه ها از رابطه \({2^n}\) استفاده می کنیم. اگر تعداد زیر مجموعه را داشته باشیم و تعداد عضو را خواسته باشند عدد داده شده را تجزیه می کنیم.
مثال
الف مجموعه ی \(A = \{ 1\,,\,2\,,\,3\,,\, \ldots \,,\,10\} \) چند زیر مجموعه دارد؟
\(n(A)\, = \,10\, \Rightarrow \,{2^n}\, = \,\,{2^n} = \,\,1024\,\) زیر مجموعه
ب یک مجموعه دارای 32 زیر مجموعه است. این مجموعه دارای چند عضو است؟
\(32\, = \,{2^5}\, \Rightarrow \,\) 5 عضو دارد
تهیه کننده : مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
نمایش مجموعه ها
نمایش مجموعه ها
الف) مجموعه اعداد طبیعی: \(\mathbb{N} = \{ 1\,,\,2\,,\,3\,,\, \ldots \} \)
ب) مجموعه اعداد حسابی: \(W = \{ 0\,,\,1\,,\,2\,,\,3\,,\, \ldots \} \)
پ) مجموعه اعداد صحیح: \(\mathbb{Z} = \{ \ldots \,,\, - 3\,,\, - 2\,,\, - 1\,,\,0\,,\,1\,,\,2\,,\,3\,,\, \ldots \} \)
ت) مجموعه اعداد طبیعی زوج: \(E = \{ 2\,,\,4\,,\,6\,,\, \ldots \} \)
ث) مجموعه اعداد طبیعی فرد: \(O = \{ 1\,,\,3\,,\,5\,,\, \ldots \} \)
ج) مجموعه اعداد گویا: \(Q\, = \,\{ \frac{a}{b}\,|\,a\,,\,b\, \in \,\mathbb{Z}\,,\,b\, \ne \,0\} \)
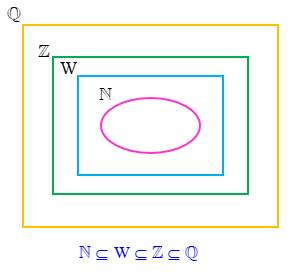
نمودار ون مجموعه ها
مجموعه ها را می توان داخل یک منحنی بسته ای نشان داد.
نمودار ون مجموعه اعداد ریاضی به صورت زیر است:
مثال
الف عضو های هر مجموعه را بنویسید:
\(A = \{ x|x \in \mathbb{Z}\,,\, - 4 \le x < 2\} \)
\(A = \{ - 4\,,\, - 3\,,\, - 2\,,\, - 1\,,\,0\,,\,1\} \)
\(B = \{ 2x - 1|x \in \mathbb{N}\,,\,x \le 3\} \)
\(B = \{ 2(1) - 1\,,\,2(2) - 1\,,\,2(3) - 1\} = \{ 1\,,\,3\,,\,5\} \)
ب صورت ریاضی هر مجموعه را بنویسید:
\(C = \{ 4\,,\,8\,,\,12\,,\, \ldots \} \)
\(C = \{ 4x|x \in \mathbb{N}\} \)
\(D = \{ - 6\,,\, - 5\,,\, - 4\,,\, \ldots \,,\,3\} \)
\(D = \{ x|x \in \mathbb{Z}\,,\, - 7 < x < 4\} \)
تهیه کننده : مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
اشتراک و اجتماع و تفاضل در مجموعه ها
اجتماع دو مجموعه
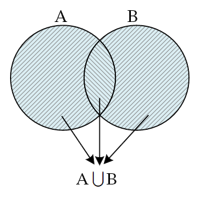
اجتماع دو مجموعه A و B شامل همه عضو هایی است که حداقل در یکی از دو مجموعه A و B باشند و اجتماع دو مجموعه A و B را بصورت \(A \cup B\) نشان می دهند.
نمودار ون اجتماع دو مجموعه A و B
اشتراک دو مجموعه
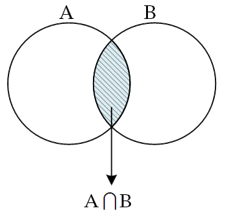
اشتراک دو مجموعه A و B شامل همه عضوهایی که هم عضو A و هم عضو B باشند و اشتراک دو مجموعه A و B را به صورت \(A \cap B\) نمایش می دهند.
نمودار ون اشتراک دو مجموعه A و B
تفاضل دو مجموعه
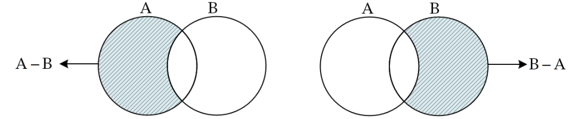
مجموعه A – B (A منهای B) شامل همه عضوهایی است که عضو مجموعه A باشند ولی عضو مجموعه B نباشند.
نمودار ون تفاضل دو مجموعه A و B
مثال
اگر مجموعه \(A = \{ 1\,,\,2\,,\,3\} \) و \(B = \{ x|x \in \mathbb{Z}\,,\, - 2 < x \le 2\} \) و \(C = \{ {x^2} + 1|x \in A\} \) باشد، عضوهای هر مجموعه را همراه با مجموعه های خواسته شده در زیر بنویسید.
\(\begin{array}{l}B = \{ x|x \in \mathbb{Z}\,,\, - 2 < x \le 2\} = \{ - 1\,,\,0\,,\,1\,,\,2\} \\\\C = \{ {x^2} + 1|x \in A\} = \{ 2\,,\,5\,,\,10\} \end{array}\)
الف \(A - C\)
\(A - C = \{ 1\,,\,2\,,\,3\} - \{ 2\,,\,5\,,\,10\} = \{ 1\,,\,3\} \)
ب \(B \cap (A \cup C)\)
\(\begin{array}{l}B \cap (A \cup C) = \{ - 1\,,\,0\,,\,1\,,\,2\} \cap (\{ 1\,,\,2\,,\,3\} \cup \{ 2\,,\,5\,,\,10\} ) = \\\\\{ - 1\,,\,0\,,\,1\,,\,2\} \cap \{ 1\,,\,2\,,\,3\,,\,5\,,\,10\} = \{ 1\,,\,2\} \end{array}\)
مثال
با توجه به هر شکل مجموعه های داده شده را هاشور بزنید؟
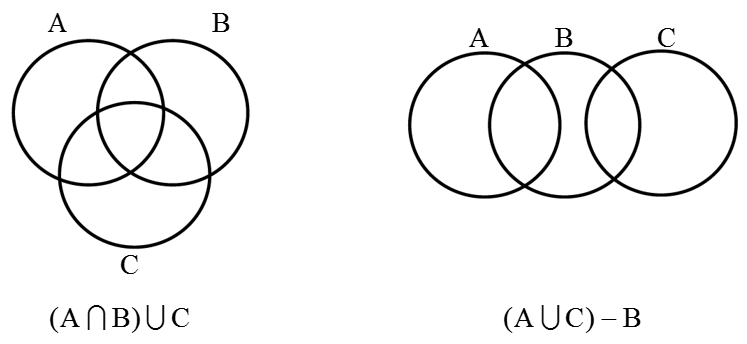
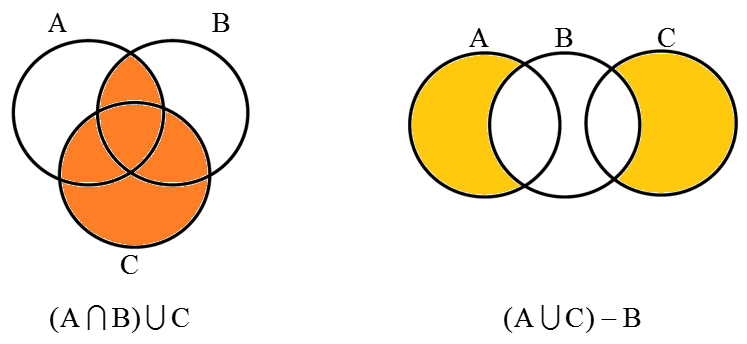
تهیه کننده : مسعود زیرکاری
مجموعه و احتمال
مجموعه و احتمال
برای به دست آوردن احتمال هر پیشامد از رابطه ی زیر استفاده می کنیم:

مثال
در پرتاب یک تاس احتمال های زیر را به دست آورید.
الف احتمال آمدن عدد اول
\(\begin{array}{l}S = \{ 1\,,\,2\,,\,3\,,\,4\,,\,5\,,\,6\} \Rightarrow n(S) = 6\\\\A = \{ 2\,,\,3\,,\,5\} \Rightarrow n(A) = 3 \Rightarrow p(A) = \frac{{n(A)}}{{n(S)}}\\\\ \Rightarrow p(A) = \frac{3}{6} = \frac{1}{2}\end{array}\)
ب احتمال آمدن عدد بزرگتر و مساوی 5
\(B = \{ 5\,,\,6\} \Rightarrow n(B) = 2 \Rightarrow p(B) = \frac{{n(B)}}{{n(S)}} \Rightarrow p(B) = \frac{2}{6} = \frac{1}{3}\)
در پرتاب دو تاس احتمال های زیر را به دست آورید.
الف) احتمال آمدن این که تاس اول عدد فرد و تاس دوم عدد کوچکتر از 3 بیاید.
کل حالت ها\(n(S) = {6^2} = 36\)
\(\begin{array}{l}A = \{ (1\,,\,1)\,,\,(1\,,\,2)\,,\,(3\,,\,1)\,,\,(3\,,\,2)\,,\,(5\,,\,1)\,,\,(5\,,\,2)\} \Rightarrow n(A) = 6\\\\ \Rightarrow p(A) = \frac{6}{{36}} = \frac{1}{6}\end{array}\)
ب) احتمال آمدن این که مجموع هر دو عدد تاس 6 شود.
\(\begin{array}{l}B = \{ (1\,,\,5)\,,\,(5\,,\,1)\,,\,(2\,,\,4)\,,\,(4\,,\,2)\,,\,(3\,,\,3)\} \Rightarrow n(B) = 5\\\\ \Rightarrow p(B) = \frac{5}{{36}}\end{array}\)
تهیه کننده : مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم



1736019749.png)