درسنامه کامل ریاضی نهم فصل 8 حجم و مساحت
تعداد بازدید : 7.59Mخلاصه نکات ریاضی نهم فصل 8 حجم و مساحت - درسنامه شب امتحان ریاضی نهم فصل 8 حجم و مساحت - جزوه شب امتحان ریاضی نهم نوبت اول فصل 8 حجم و مساحت
انواع حجم
حجم
مقدار فضایی را که یک جسم اشغال میکند حجم (گنجایش) نام دارد و حجم را با حرف انگلیسی (v) نشان می دهند.
انواع حجم
۱) حجم منشوری
۲) حجم هرمی یا مخروطی
۳) حجم کروی
دایره
مجموعه نقاطی از صفحه که فاصله تمام نقاط از یک نقطه به نام (مرکز دایره) به یک اندازه باشد. به این فاصله نقاط صفحه تا مرکز دایره (شعاع دایره ) می گویند .
دایره را به اختصار به صورت C(O,R) نشان می دهند.
C=دایره O=مرکز R=شعاع
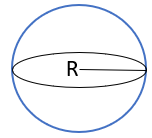
کره
مجموعه نقاطی از فضا که فاصله تمام نقاط از یک نقطه به نام مرکز کره به یک اندازه باشد به این فاصله نقاط صفحه تا مرکز دایره شعاع کره می گویند.
مانند :
کره زمین و توپ
فرمول مساحت کره : \(S = 4\pi {r^2}\)
فرمول حجم کره :\(v = \frac{4}{3}\pi {r^3}\)
مثال
حجم و مساحت کره با قطر ۴ سانتی متر را به دست آورید.
\(\begin{array}{l}R = 4 \div 2 = 2\\\\\left\{ \begin{array}{l}v = \frac{4}{3}\pi {r^2} = \frac{4}{3} \times 3/14 \times {2^3} = 50/24\\\\S = 4\pi {r^2} = 4 \times 3/14 \times {2^2} = 50/24\end{array} \right.\end{array}\)
مثال
نسبت عددی حجم کره به مساحت کره چند است.
\(\frac{v}{s} = \frac{{\frac{4}{3}\pi {r^2}}}{{4\pi {r^2}}} = \frac{1}{3}r\)
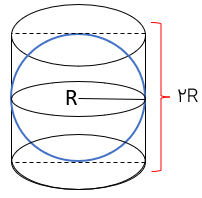
اگر کره به طور کامل داخل استوانه قرار گیرد می گوییم کره بر استوانه محاط شده و استوانه بر کره محیط شده است.
مثال
کره ای در استوانه ای به قطر ۶ سانتی متر محاط شده است :
الف) حجم کره را به دست آورید.
\(\begin{array}{l}R = 6 \div 2 = 3cm\\\\v = \frac{4}{3}\pi {r^2} = \frac{4}{3} \times 3/14 \times {3^3} = 113/04c{m^3}\end{array}\)
ب) حجم استوانه را به دست آورید.
\(v = s \times h = (3 \times 3 \times 3/4) \times 6 = 169/56c{m^3}\)
ج) حجم فضای بین کره و استوانه را به دست آورید.
\(169/56 - 113/04 = 56/52c{m^3}\)
1 از دوران نیم دایره حول قطر کره حاصل می شود.
2 از دوران ربع دایره حول شعاع نیم کره حاصل می شود.
3 برای به دست آوردن حجم نیم کره می توان از رابطه ی \(v = \frac{2}{3}\pi {r^3}\) استفاده کرد.
مثال
حجم حاصل از دوران ربع دایره حول شعاع ۴ سانتی متر را به دست آورید. (بر حسب\(\pi \))
)از دوران ربع دایره حول شعاع نیم کره حاصل می شود)
\(v = \frac{2}{3}\pi {r^3} = \frac{2}{3}\pi \times {4^3} = 42/66\)
اگر شعاع کره را n برابر کنیم مساحت کره \({n^2}\) و حجم کره \({n^3}\) برابر خواهد شد.
مثال
اگر شعاع کره ای را ۴ برابر کنیم مساحت و حجم کره چند برابر خواهد شد؟
\(\begin{array}{l}s = {n^2} = {4^2} = 16\\\\v = {n^3} = {4^3} = 64\end{array}\)
تهیه کننده:مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
هرم
هرم
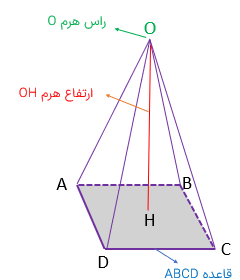
هرم شکل فضایی که سطح جانبی آن مثلث و وجه زیرین (قاعده( آن چند ضلعی محدب باشد.
به فاصله راس هرم تا قاعده ارتفاع هرم می گویند.
حجم هرم
الف( کلامی
ارتفاع × مساحت قاعده ×\(\frac{1}{3}\) = حجم هرم
ب جبری :
\(v = \frac{1}{3}s.h\)
مثال
حجم هرم مربع القاعده ای به ضلع ۵ سانتی متر و ارتفاع ۶ سانتی متر را به دست آورید.
\(v = \frac{1}{3}s.h = \frac{1}{3} \times (5 \times 5) \times 6 = 50c{m^3}\)
) خودش × یک ضلع = s مربع)
مثال
قاعده لوزی با قطرهای ۶ و ۸ سانتی متر است. اگر ارتفاع هرم ۵ سانتی متر باشد حجم هرم چند سانتی متر مکعب است؟
(2÷حاصل ضرب دو قطر = لوزیs )
\(v = \frac{1}{3}s.h = \frac{1}{3} \times \left( {\frac{{6 \times 8}}{2}} \right) \times 5 = 40c{m^3}\)
اگر دو هرم دارای قاعده های هم مساحت و ارتفاع یکسان باشند. دارای حجم برابر هستند.
تهیه کننده:مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
مخروط
مخروط
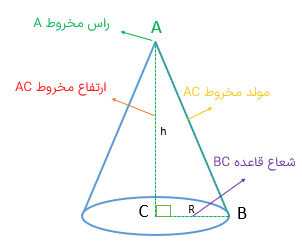
شکلی شبیه ای هرم منتظم که قاعده آن دایره و پای ارتفاع مخروط مرکز دایره باشد.
حجم مخروط
الف( کلامی :
ارتفاع × مساحت قاعده ×\(\frac{1}{3}\) = حجم مخروط
ب( جبری :
\(v = \frac{1}{3}s.h = \frac{1}{3}\pi {r^2}h\)
مثال
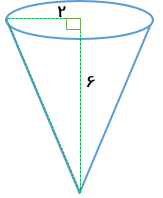
حجم مخروط زیر را حساب کنید.
\(v = \frac{1}{3}s.h = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \times 3/14 \times {2^2} \times 6 = 25/12c{m^3}\)
مثال
گنجایش مخروطی ۴۷۱۰۰ لیتر است. اگر شعاع قاعده ۳ متر باشد ارتفاع مخروط چند متر است؟
هر متر مکعب ۱۰۰۰ لیتر است.
\(47100 \div 1000 = 47/1\,\,{m^3}\) حجم مخروط
\(v = \frac{1}{3}\pi {r^2}h \Rightarrow 47/1 = \frac{1}{3} \times 3/14 \times {3^2} \times h \Rightarrow h = \frac{{47/1}}{{9/42}} = 5\,\,m\)
از دوران مثلث قائم الزاویه حول یک ضلع قائم آن مخروط حاصل میشود ضلعی که دوران روی آن انجام شده است ارتفاع مخروط و ضلع دیگر شعاع قاعده نام دارد.
مثال
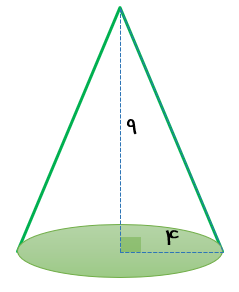
مثلث قائم الزاویه با اضلاع قائم ۴ و ۹ سانتی متر را روی ضلع بزرگتر دوران داده ایم حجم شکل حاصل چند سانتی متر مکعب است؟
\(v = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \times 3/14 \times {4^2} \times 9 = 150/72c{m^3}\)
مثلث قائم الزاویه ABC را روی حول ضلع AB دوران داده.ایم حجم شکل حاصل را به دست آورید.
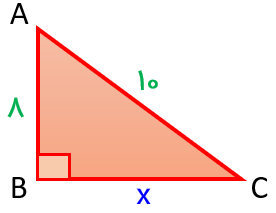
شعاع قاعده\({x^2} = {10^2} - {8^2} = 100 - 64 = 36 \Rightarrow x = 6\) :رابطه فیثاغورس
\(v = \frac{1}{3}\pi {r^2}h = \frac{1}{3} \times 3/14 \times {6^2} \times 8 = 301/44c{m^3}\)
1 از دوران مستطیل و مربع حول یک ضلع آن استوانه تشکیل می شود.
2 مساحت جانبی و مساحت کل استوانه از رابطه های زیر به دست می آید :
\( \Rightarrow s = p \times h\) ارتفاع × محیط قاعده = مساحت جانبی
Sدو قاعده + S جانبی = S کل\( \Rightarrow \)مساحت دو قاعده + مساحت جانبی = مساحت کل
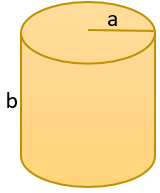
نسبت حجم به مساحت کل استوانه ای را به دست آورید که شعاع قاعده آن a و ارتفاع آن b باشد.
\(v = s \times h = \left( {a \times a \times \pi } \right) \times b = \pi {a^2}b\)
جانبی \(s = p \times h = \left( {2 \times a \times \pi } \right) \times b = 2\pi ab\)
S \( = 2\pi ab + 2{a^2}\pi = 2\pi a\left( {b + a} \right)\) دو قاعده + S جانبی = S کل
\(\frac{v}{s} = \frac{{\pi {a^2}b}}{{2\pi a\left( {a + b} \right)}} = \frac{{ab}}{{2\left( {a + b} \right)}}\)
تهیه کننده:مسعود زیرکاری



1736019749.png)