درسنامه کامل ریاضی نهم فصل 6 خط و معادله های خطی
تعداد بازدید : 7.59Mخلاصه نکات ریاضی نهم فصل 6 خط و معادله های خطی - درسنامه شب امتحان ریاضی نهم فصل 6 خط و معادله های خطی - جزوه شب امتحان ریاضی نهم نوبت اول فصل 6 خط و معادله های خطی
معادله خط
معادله خط
رابطه ای است که بین نقاط تشکیل دهنده یک خط وجود دارد.
1 فرم کلی معادله خط به صورت y = ax + b) ( می باشد.
2 در صورتی که نمودار رابطه ی بین دو مقدار به صورت خط راست باشد. آن دو مقدار با هم رابطه خطی دارند.
مثال
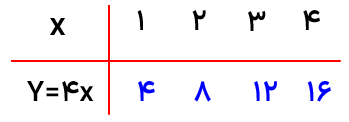
آیا رابطه بین یک ضلع مربع و محیط مربع رابطه ی خطی است؟ چرا؟
بله چون افزایش یک ضلع مربع با افزایش محیط مربع یک مقدار ثابت است .(ضلع مربع را X و محیط مربع را y در نظر میگیریم پس خواهیم داشت :x 4=y )
مثال
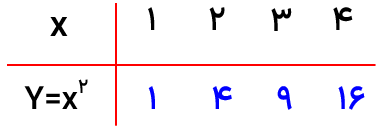
آیا رابطه بین یک ضلع مربع و مساحت مربع رابطه ی خطی است؟ چرا؟
خیر. چون افزایش یک ضلع مربع با افزایش مساحت مربع مقدار ثابتی نیست. (ضلع مربع را x و مساحت مربع را y در نظر میگیریم بنابرین خواهیم داشت :\(y = {x^2}\) )
انواع معادله خط
۱) مبدا گذر (فرم کلی : y=ax )
۲) غیر مبدا گذر (فرم کلی : y = ax + b)
۳) خطوط موازی با محور (فرم کلی : m , x = n = y)
تهیه کننده: مسعود زیر کاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
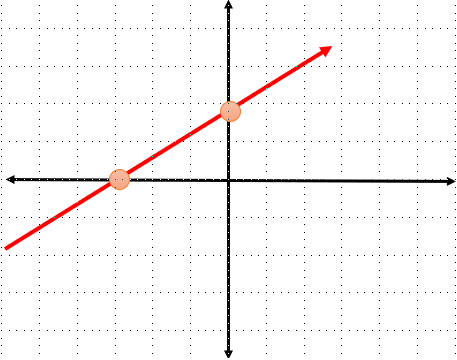
ترسیم خط در دستگاه مختصات
رسم یک خط
برای رسم یک خط در دستگاه مختصات نیاز به مختصات دو نقطه است.
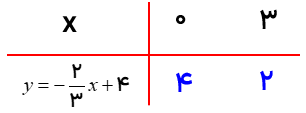
اگر در فرم کلی استاندارد معادله خط عدد قبل از x عدد صحیح باشد در جدول به جای اعداد ( 0 و 1) قرار می دهیم ، و عدد قبل از x عدد کسری باشد به جای x اعداد ( صفر و مخرج کسر ) قرار می دهیم.
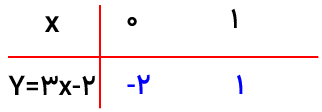
مثال
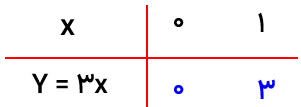
معادله خط y=3xرا در دستگاه مختصات رسم کنید.
خط مبدا گذر:
مثال
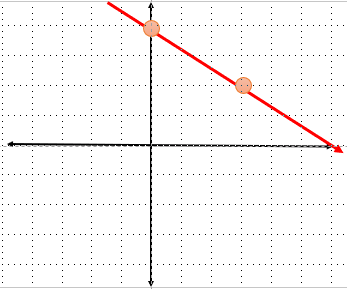
معادله خط \(y = - \frac{2}{3}x + 4\) را در دستگاه مختصات رسم کنید.
خط غیر مبدا گذر:
مثال
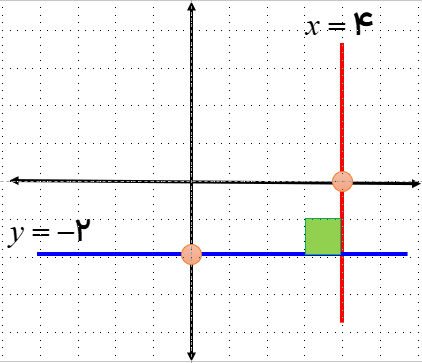
معادلات خط ۲- = y و ۴ = x را در دستگاه مختصات رسم کنید.
برای رسم این خط ها نیاز به جدول نیست. فقط کافی است هر نقطه داده شده را در دستگاه مختصات مشخص کرد سپس خطی موازی با محور از روی آن نقطه رسم کرد.
خط موازی با محور
زاویه ی بین خطوط موازی با محور ۹۰ درجه است.
شرط این که نقطه روی یک خط قرار گیرد این است که مختصات آن نقطه در معادله خط صدق کند که برای این کار دو روش وجود دارد:
۱ روش تحلیلی (جایگزینی مختصات نقطه در معادله خط)
۲ روش ترسیمی
مثال
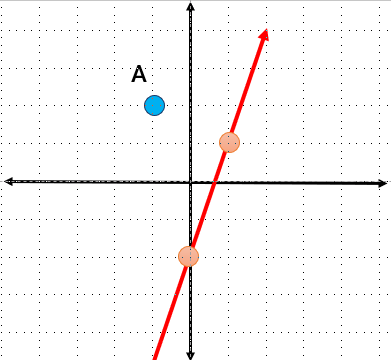
آیا نقطه ی \(A = \left[ \begin{array}{l} - 1\\2\end{array} \right]\) روی خط ۲ – ۳x = y قرار دارد؟
روش تحلیلی :قرار ندارد چون دو طرف تساوی برابر نیست :
\((x = - 1\,,\,y = 2) \Rightarrow 2 = 3( - 1) - 2 \Rightarrow 2 \ne - 5\)
روش ترسیمی : خط داده شده را در دستگاه مختصات رسم کرده سپس نقطه A را نیز در دستگاه مختصات مشخص می کنیم :
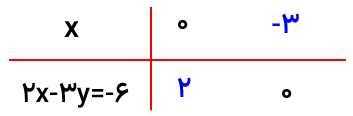
برای رسم معادلات خطی که به صورت (ax + by = c) هستند. در جدول یک بار به جای x و یک بار به جای yصفر قرار می دهیم
مثال
معادله خط ۶ = y۳x - ۲ را در دستگاه مختصات رسم کنید.
تهیه کننده: مسعود زیرکاری
جزوات جامع پایه نهم
جزوه جامع ریاضی نهم فصل 1 مجموعه ها
جزوه جامع ریاضی نهم فصل 2 عددهای حقیقی
جزوه جامع ریاضی نهم فصل 3 استدلال و اثبات در هندسه
جزوه جامع ریاضی نهم فصل 4 توان و ریشه
جزوه جامع ریاضی نهم فصل 5 عبارت های جبری
جزوه جامع ریاضی نهم فصل 6 خط و معادله های خطی
جزوه جامع ریاضی نهم فصل 7 عبارت های گویا
جزوه جامع ریاضی نهم فصل 8 حجم و مساحت
شیب خط و عرض از مبدا
شیب خط
زاویه ای بین سمت راست محور طول ها با خط داده شده را می گویند.
عرض از مبدا
نقطه ای که خط داده شده محور عرض ها را در آن نقطه قطع میکند را عرض از مبدا می گویند.
1 در فرم کلی معادله خط (y=ax + b ) ضریب x یعنی عدد a شیب خط و عدد b عرض از مبدا نام دارد.
مانند : در معادله خط \(y = - \frac{1}{4}x + 1\) (عدد شیب خط : \( - \frac{1}{3}\) ) و عدد (عرض از مبدا : ۱) می باشد.
2 برای به دست آوردن شیب خط و عرض مبدا باید معادله خط به فرم کلی (y= ax + b)مرتب شود.
مثال
شیب خط و عرض از مبدا معادله های خطی زیر را به دست آورید.
الف) \( - 5x + 2y = - 6\)
\(2y = 5x - 6 \Rightarrow \frac{{2y}}{2} = \frac{{5x}}{2} - \frac{6}{2} \Rightarrow y = \frac{5}{2}x - 3\)
(عرض از مبدا : -3 و شیب خط ب خط :\(\frac{5}{2}\))
ب) \(2y = - 4x\)
\(\frac{{2y}}{2} = \frac{{ - 4x}}{2} \Rightarrow y - 2x\)
) عرض از مبدا : ۰ و شیب خط: -2 )
تهیه کننده: مسعود زیرکاری
طول از مبدا
طول از مبدا
نقطه ای که خط داده شده محور طول ها را در آن نقطه قطع میکند را طول از مبدا می گویند.
برای به دست آوردن طول از مبدا در معادله خط به جای y صفر قرار می دهیم.
مثال
طول از مبدا معادله خط \(\frac{2}{3}x - \frac{1}{4}y = - 5\) را به دست آورید.
\(y = 0 \Rightarrow \frac{2}{3}x - \frac{1}{4}(0) = - 5 \Rightarrow \frac{2}{3}x = - 5 \Rightarrow x = \frac{{ - 5}}{{\frac{2}{3}}} = - \frac{{15}}{2} \Rightarrow x = - \frac{{15}}{2}\)
1 دو خط در صورتی موازی هستند که شیب دو خط برابر باشند . مانند :\(y = - 3x\,,\,y = - 3x + 5\)
2 دو خط در صورتی بر هم عمود هستند که شیب دو خط قرینه و معکوس یکدیگر باشند یا حاصل ضرب دو شیب خط برابر با عدد ۱ - شود. مانند : \(y = 2x + 3\,,\,y = - \frac{1}{2}x - 2\)
مثال
معادله خطی بنویسید که با خط ۵ =y ۳ - X موازی و از نقطه ی \(A = \left[ \begin{array}{l}0\\ - 2\end{array} \right]\) بگذرد.
ابتدا معادله خط را مرتب کرده تا شیب خط مشخص شود:
\(\begin{array}{l} - 3y = - x + 5 \Rightarrow \frac{{ - 3y}}{{ - 3}} = - \frac{x}{{ - 3}} + \frac{5}{{ - 3}} \Rightarrow \frac{1}{3}x - \frac{5}{3} \Rightarrow a = \frac{1}{3}\\(a = \frac{1}{{3\,}}\,\,\,,\,\,\,\,b = - 2)\\\\y = ax + b \Rightarrow y = \frac{1}{3}x - 2\end{array}\)
معادله خط جدید:\(y = \frac{1}{3}x - 2\)
مثال
معادله خطی بنویسید که با خط\(y = - \frac{1}{5} + 2\) عمود باشد و از نقطه ی \(B = \left[ \begin{array}{l} - 1\\2\end{array} \right]\) بگذرد.
شیب خط مشخص است پس باید عرض از مبدا را به دست آوریم :
\(\begin{array}{l}(a = 5\,\,,\,\,x = - 1\,\,\,,\,\,\,y = 2)\\\\y = ax + b \Rightarrow 2 = 5( - 1) + b \Rightarrow b = 7\\(b = 7)\\\\y = ax + b \Rightarrow y = 5x + 7\end{array}\)
معادله خط جدید:\(y = 5x + 7\)
برای به دست آوردن شیب خطی که از دو نقطه میگذرد از رابطه ی زیر استفاده می کنیم :
معادله خطی بنویسید که از نقاط \(B = \left[ \begin{array}{l} - 1\\4\end{array} \right]\,\,\,,\,\,\,A = \left[ \begin{array}{l}2\\3\end{array} \right]\) بگذرد.
\(\begin{array}{l}a = \frac{{4 - 3}}{{ - 1 - 2}} = - \frac{1}{3}\,\,\,\,,\,\,\,\,(x = 2\,,\,y = 3)\\\\y = ax + b \Rightarrow y = - \frac{1}{3}x + \frac{{11}}{3}\end{array}\)
معادله خط جدید:\(y = - \frac{1}{3}x + \frac{{11}}{3}\)
معادله خط محور طول ها (y=0) و معادله خط محور عرض ها ( 0= x (و معادله خط نیمساز ربع اول و سومx) =y ) و معادله خط نیمساز ربع دوم و چهارم y =-x) ( می باشد.
تهیه کننده: مسعود زیرکاری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
دستگاه معادلات خطی
دستگاه معادلات خطی
برای حل دستگاه معادلات خطی از روش های زیر می توان استفاده کرد :
1- روش حذفی:
در این روش یکی از متغیرها را حذف کرده سپس با جایگزینی متغیر دوم به دست می آید.
مثال
دستگاه معادلات دو مجهولی زیر را حل کنید.
\(\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4 + y = - 7\end{array} \right.\)
\(\begin{array}{l}2x + 3(1) = 7 \Rightarrow 2x = 4 \Rightarrow x = 2\\\\\mathop {}\limits^{2 \times } \,\,\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4 + y = - 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}4x + 6y = 14\\\\ - 4 + y = - 7\end{array} \right. \Rightarrow 7y = 7 \Rightarrow y = 1\end{array}\)
جواب دستگاه دو مجهولی: \(A = \left[ \begin{array}{l}2\\1\end{array} \right]\)
2- روش جایگزینی( تبدیلی):
در این روش یکی از معادلات را بر حسب یک متغیر مرتب کرده و مقدار آن را در معادله دوم قرار می دهیم.
مثال
دستگاه معادلات دو مجهولی زیر را حل کنید. (روش جایگزینی)
\(\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4x + y = - 7\end{array} \right.\)
ابتدا معادله اول را برحسب xمرتب می کنیم سپس مقدار xرا در معادله پایین قرار می دهیم.
\(\begin{array}{l}\left\{ \begin{array}{l}2x + 3y = 7\\\\ - 4x + y = - 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2x = - 3y + 7 \Rightarrow x = - \frac{3}{2}y + \frac{7}{2}\\ - 4( - \frac{3}{2}y + \frac{7}{2}) + y = - 7 \Rightarrow 6y - 14 + y = - 7 \Rightarrow 7y = 7 \Rightarrow y = 1\end{array} \right.\\\\x = - \frac{3}{2}(1) + \frac{7}{2} \Rightarrow x = - \frac{3}{2} = \frac{7}{2} = \frac{4}{2} = 2 \Rightarrow x = 2\end{array}\)
جواب دستگاه دو مجهولی :\(A = \left[ \begin{array}{l}2\\1\end{array} \right]\)
برای حل بعضی از مسایل میتوان از دستگاه دو مجهولی استفاده کرد و به یکی از روش های آن را حل کرد.
سن برادر علی ۳ برابر سن او است،و اختلاف سن آنها ۱۸ سال است. سن هر یک را به دست آورید. (به روش جایگزینی)
)سن برادر علی را X و سن علی را y فرض می کنیم.(
\(\begin{array}{l}\left\{ \begin{array}{l}x = 3y\\\\x - y = 18\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 3y\\\\3y - y = 18 \Rightarrow 2y = 18 \Rightarrow y = 9\end{array} \right.\\\\x = 3(9) = 27 \Rightarrow x = 27\end{array}\)
علی9 سال و برادرش 27 سال دارد.
تهیه کننده: مسعود زیرکاری



1736019749.png)