درسنامه کامل ریاضی دهم فصل 1 مجموعه، الگو و دنباله
تعداد بازدید : 7.59Mخلاصه نکات ریاضی دهم فصل 1 مجموعه، الگو و دنباله - درسنامه شب امتحان ریاضی دهم فصل 1 مجموعه، الگو و دنباله - جزوه شب امتحان ریاضی دهم نوبت اول فصل 1 مجموعه، الگو و دنباله
مجموعه های اعداد
مجموعه های اعداد
ابتدایی ترین مجموعه مورد استفاده بشر همان طور که می دانید مجموعه اعداد طبیعی بوده است. مجموعه اعداد طبیعی بصورت زیر است:
\(\mathbb{N} = \{ 1,2,3,...\} \)
لازم است خاصیتی جالب را در مورد مجموعه \(\mathbb{N}\) معرفی کنیم. چنانچه دو عدد دلخواه از اعداد طبیعی را باهم جمع کنیم حاصل باز هم عدد طبیعی است بعنوان مثال :
\(1 + 3 = 4 \in \mathbb{N}\)
در حالت کلی اگر a، b دو عدد طبیعی باشند واضح است که \(a + b\) نیز عددی طبیعی است. این خاصیت را اصطلاحا بسته بودن \(\mathbb{N}\) نسبت به عمل + می نامیم.
خاصیت بسته بودن برای اعداد طبیعی در اعمال ضرب، تقسیم و توان نیز صادق است ولی در عمل تفریق صادق نیست.
مثال
1 مجموعه \(A = \{ {2^n}|n \in \mathbb{N}\} \) را در نظر بگیرید. نشان دهید این مجموعه نسبت به عمل توان بسته است.
\(\begin{array}{l}n \in \mathbb{N} \to n = \{ 1,2,3,...\} \\ \to {2^n} \in \mathbb{N}\end{array}\)
عدد 2 به هر تعداد در خودش ضرب شود همچنان جزو اعداد طبیعی خواهد ماند.
2 آیا مجموعه \(A = \{ {a^2} - b|a,b \in \mathbb{N}\} \) نسبت به اعداد طبیعی بسته است؟ در صورت منفی بودن جواب مثال نقضی ارائه دهید.
خیر زیرا؛
\(\begin{array}{l}a,b \in \mathbb{N} \to a,b = \{ 1,2,3,...\} \\a = 2,b = 5 \to {a^2} - b = {2^2} - 5 = 4 - 5 = - 1\\ \to {a^2} - b = - 1 \to - 1 \notin \mathbb{N}\end{array}\)
حال با توجه به مثال بالا می توان متوجه ضعف مجموعه اعداد طبیعی شد. \(\mathbb{N}\) نسبت به تفریق بسته نیست. این بزرگترین ضعف \(\mathbb{N}\) است. زمانی که بشر برای معاملات خود متوجه شد که مقروض بودن را نمی توان با اعداد طبیعی نمایش داد خلاء اعداد صحیح را حس کرد و مجبور شد اعداد صحیح را بکار بگیرد.
مجموعه اعداد صحیح را که با نماد \(\mathbb{Z}\) نشان می دهیم عبارت است از :
\(\mathbb{Z} = \{ ..., - 2, - 1,0,1,2,...\} \)
اینکه اعداد صحیح را با حرف \(\mathbb{Z}\) نمایش می دهند به خاطر کلمه Zahlen می باشد که لغتی آلمانی است. اعداد صحیح نیز به نوبه ی خود دارای ضعف بسته نبودن نسبت به عمل تقسیم بود به عنوان مثال دقت کنید که :
\(\frac{2}{4} = \frac{1}{2} = 0/5 \notin \mathbb{Z}\)
برای برطرف کردن این ضعف \(\mathbb{Z}\) مجموعه ای مورد نیاز بود که شامل تمام کسرهای ممکن که می توان به کمک اعداد صحیح ساخت باشد. این مجموعه را اعداد گویا می نامیم و بصورت زیر تعریف می کنیم:
مجموعه اعداد گویا را که با نماد \(\mathbb{Q}\) نشان می دهیم (\(\mathbb{Q}\) حرف اول کلمه Quotient به معنای خارج قست) بصورت زیر تعریف می کنیم:
\(\mathbb{Q} = \left\{ {\frac{a}{b}|a,b \in \mathbb{Z},b \ne 0} \right\}\)
مجموعه اعداد گویا کوچکترین مجموعه ای است که نسبت به هر چهار عمل اصلی بسته است، با این حال همین مجموعه هم بی نقص نیست.
می دانیم که قطر مربعی به ضلع یک عددی غیر گویا یا اصم است. این عدد عددی نیست جز \(\sqrt 2 \).
می توان ثابت کرد که \(\sqrt 2 \) را نمی توان بصورت یک کسر نوشت به عبارت بهتر به ازای هر دو عدد صحیح دلخواه a و b همواره داریم: \(a,b \ne \sqrt 2 \)
مجموعه اعداد گنگ را با نماد \(\mathbb{Q}'\) نشان می دهیم. یکی دیگر از اعداد گنگی، که قدمت زیادی دارد عدد  است. نسبت محیط دایره به قطر آن عدد \(\pi \) است. (داستان پیدایش عدد پی با مسأله تربیع دایره در ارتباط تنگاتنگ است.)
است. نسبت محیط دایره به قطر آن عدد \(\pi \) است. (داستان پیدایش عدد پی با مسأله تربیع دایره در ارتباط تنگاتنگ است.)
تاکنون با مجموعه های \(\mathbb{Q}',\mathbb{Q},\mathbb{Z},\mathbb{N}\) آشنا شده اید. رابطه بین سه مجموعه اول به صورت زیر است:
\(\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q}\)
در این رابطه مجموعه \(\mathbb{Q}'\) چه جایگاهی دارد؟ حال می توان مجموعه اعداد حقیقی را هم تعریف کرد.
مجموعه اعداد حقیقی را که با نماد \(\mathbb{R}\) نشان می دهیم برابر است با :
\(\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}'\)
(علامت \( \cup \) به معنای اجتماع است.)
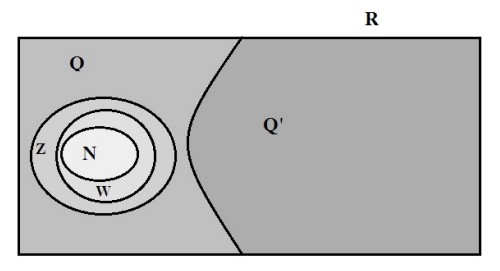
رابطه ی بین مجموعه اعداد
متناظر به هر عدد حقیقی نقطه ای روی محور اعداد حقیقی وجود دارد. در اشکال زیر موقعیت برخی از اعداد روی محور نشان داده شده است.
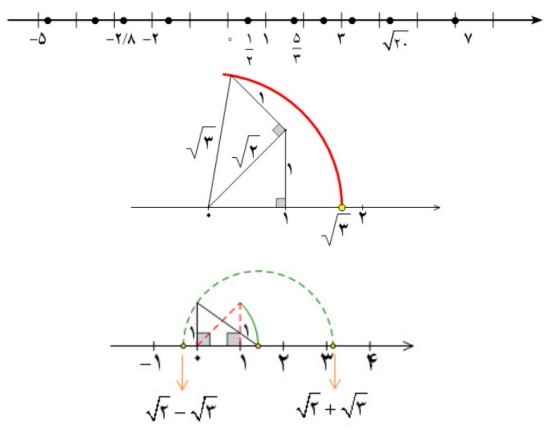
نمایش اعداد گویا و گنگ روی محور اعداد
اگر به شکل با دقت نگاه کنید متوجه خواهید شد که این شکل راه حل بسیار زیبایی را به شما معرفی کرده است و ارزش آن بیش از یک شکل ساده است. سرانجام آخرین مجموعه از اعداد را که بزرگتر از \(\mathbb{N}\) و کوچکتر از \(\mathbb{Z}\) است را معرفی می کنیم. مجموعه اعداد حسابی که با نماد W نشان می دهیم عبارتست از:
\(W = \{ 0,2,3,...\} \)
جاهای خالی را با مجموعه مناسب کامل کنید.
الف \(\mathbb{R} - \mathbb{Q} = \)
\(\mathbb{R} - \mathbb{Q} = \mathbb{Q}'\)
ب \(\mathbb{Z} - W = \)
\(\mathbb{Z} - W = \{ ..., - 2, - 1\} \)
پ \(\mathbb{N} - W = \)
\(\mathbb{N} - W = \emptyset \)
ت \(\mathbb{Q}' - \mathbb{Q} = \)
\(\mathbb{Q}' - \mathbb{Q} = \mathbb{Q}'\)
تهیه کننده: فرهاد صمدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
بازه های اعداد حقیقی
بازه های اعداد حقیقی
برای ورود به مطلب و آشنایی با بازه ها دو نامعادله زیر را در نظر بگیرید:
1)
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a} - 1 \le \frac{{2x + 1}}{3}\langle 3\)
2)
\(3x + 1\langle 7\)
با حل این دو نامعادله مجموعه جواب معادله شماره ١ عبارتست از \(\{ x \in \mathbb{R}| - 2 \le x\langle 4\} \) و مجموعه جواب معادله شماره ٢ عبارت است از \(\{ x \in \mathbb{R}|x\langle 2\} \).
آیا می توان مجموعه جواب را با نمادی ساده تر از مجموعه های فوق نوشت؟ جواب مثبت است. بازه ها جواب گوی ما برای این ساده نویسی هستند. مجموعه جواب نامعادله ١ بازه ی \([ - 2,4)\) است و مجموعه جواب نامعادله شماره ٢ بازه ی بی کران \(\left( { - \infty ,2} \right)\) است. حال به سراغ تعریف بازه ها می رویم.
یک بازه، زیر مجموعه ای از اعداد حقیقی است که بصورت های زیر تعریف می شود:
بازه ی باز:
\(\left( {a,b} \right) = \{ x \in \mathbb{R}|a\langle x\langle b\} \)
بازه ی نیم باز:
\(\left[ {a,b} \right) = \{ x \in \mathbb{R}|a \le x\langle b\} \)
بازه ی بسته:
\(\left[ {a,b} \right] = \{ x \in \mathbb{R}|a \le x \le b\} \)
بازه ی باز بی کران:
\(\left( {a, + \infty } \right) = \{ x \in \mathbb{R}|a\rangle x\} \)
بازه ی نیم باز بی کران:
\(\left[ {a, + \infty } \right) = \{ x \in \mathbb{R}|a\rangle x\} \)
بازه ی باز بی کران:
\(\left( { - \infty ,a} \right) = \{ x \in \mathbb{R}|a\langle x\} \)
بازه ی نیم باز بی کران:
\(\left( { - \infty ,a} \right] = \{ x \in \mathbb{R}|a\langle x\} \)
اغلب بجای اصطلاح نیم باز از اصطلاح نیم بسته هم استفاده می شود. نماد ∞ که بی نهایت خوانده می شود (مثبت بی نهایت یا منفی بی نهایت) یک عدد حقیقی نیست فقط نمادی است برای اینکه نشان دهیم بازه بی کران است. یعنی هر عددی خواه بسیار بزرگ یا خواه بسیار کوچک در این بازه ها می تواند وجود داشته باشد.
در اشکال زیر چند بازه را بعنوان مثال روی محور اعداد حقیقی نمایش داده ایم.

درست و نادرست را بررسی کنید و جاهای خالی را با عبارت مناسب پر کنید.
الف \(3 \in \left[ { - 1,\sqrt {10} } \right)\)
درست زیرا؛
\(\sqrt {10} = 3/16 \to 3 \in \left[ { - 1,\sqrt {10} } \right)\)
ب \(\frac{1}{{\sqrt 2 }} \in \left( {0,1} \right]\)
درست زیرا؛
\(\begin{array}{l}\sqrt 2 = 1/41 \to \frac{1}{{\sqrt 2 }} = \frac{1}{{1/41}} = 0/7\\0/7 \in \left( {0,1} \right] \to \frac{1}{{\sqrt 2 }} \in \left( {0,1} \right]\end{array}\)
پ \(\mathbb{Z} - \mathbb{N} = W\)
درست است.
ت \(\sqrt {841} \in \mathbb{Q}\)
درست زیرا؛
\(\begin{array}{l}\sqrt {841} = 29 \to 29 \in \mathbb{N}\\\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \to \sqrt {841} \in \mathbb{Q}\end{array}\)
تهیه کننده: فرهاد صمدی
جزوات جامع پایه دهم
جزوه جامع ریاضی دهم فصل 1 مجموعه، الگو و دنباله
جزوه جامع ریاضی دهم فصل 2 مثلثات
جزوه جامع ریاضی دهم فصل 3 توان های گویا و عبارت های جبری
جزوه جامع ریاضی دهم فصل 4 معادله ها و نامعادله ها
جزوه جامع ریاضی دهم فصل 5 تابع
جزوه جامع ریاضی دهم فصل 6 شمارش، بدون شمردن
جزوه جامع ریاضی دهم فصل 7 آمار و احتمال
مجموعه های متناهی و نامتناهی
مجموعه های متناهی و نامتناهی
در این بخش می خواهیم در مورد تعداد اعضای یک مجموعه صحبت کنیم.
مجموعه ای چون A را یک مجموعه متناهی (باپایان) گوییم هرگاه تعداد اعضای آن را بتوان با یک عدد حسابی نمایش داد. اگر تعداد اعضای یک مجموعه را با نماد \(\left| A \right|\) |نمایش دهیم متناهی بودن یک مجموعه چون A به معنای آن است که به ازای یک عدد حسابی مثل k داریم \(\left| A \right| = k\)، در غیر اینصورت مجموعه را نامتناهی (بی پایان) گوییم.
مثال
مجموعه های زیر را بررسی کنید و متناهی یا نامتناهی بودن آنها را معین کنید.
الف مجموعه دانش آموزان سال دهم رشته ریاضی در کشور.
متناهی
ب تعداد اعداد ٣ رقمی و بزرگتر از ۵00.
متناهی (\(\{ x \in \mathbb{N}|500\langle x\langle 1000\} \))
پ تعداد اعداد اول.
نامتناهی
ج مجموعه اعداد طبیعی فرد.
نامتناهی
اگر مجموعه ای چون A دارای زیرمجموعه ای چون B باشد (\(B \subseteq A\)) به طوری که B نامتناهی باشد آنگاه بناچار خود A نیز نامتناهی است. در نتیجه چون اعداد گویای واقع در بازه ی (\(0,1\)) نامتناهی هستند پس \(\mathbb{Q}\) هم نامتناهی است و به همین ترتیب \(\mathbb{R}\) نیز نامتناهی است زیرا، (\(\mathbb{Q} \subseteq \mathbb{R}\)).
متناهی یا نامتناهی بودن مجموعه های زیر را بررسی کنید.
الف مجموعه کلمات بکار رفته در کتاب ریاضی دهم.
متناهی
ب مجموعه مضارب مثبت عدد ۵.
نامتناهی
پ مجموعه پلنگ های زنده در قاره آفریقا.
متناهی
ج مجموعه تمام زیر مجموعه های \(\mathbb{N}\).
نامتناهی
د مجموعه تمام موبایل های تولید شده در ٢٠ سال گذشته.
متناهی
و مجموعه تمام اعدادی که در تقسیم بر ۵ باقیمانده ١ دارند.
نامتناهی
تهیه کننده: فرهاد صمدی
متمم یک مجموعه
متمم یک مجموعه
مجموعه مرجع
در هر مبحث مجموعه ای که همه مجموعه های مورد بحث زیر مجموعه آن باشند را مجموعه مرجع یا مجموعه جهانی می نامند و با حرف U نشان می دهند. در این حالت اگر \(A \subseteq U\) مجموعه ای دلخواه باشد، \(U - A\) را با نماد \(A'\) نشان می دهیم و آن را متمم A می نامیم. به عبارت بهتر \(A'\) شامل اعضایی از U است که در A نیستند.
در شکل زیر رابطه بین مجموعه های \(A,A',U\) دیده می شود.
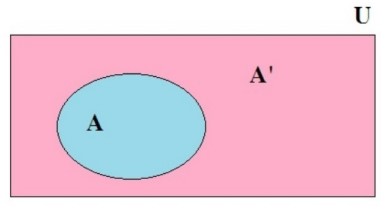
بطور معمول در هر بحثی مجموعه مرجع را معرفی می کنند. چنانچه در بحثی مجموعه مرجع را معرفی نکردیم شما می توانید بزرگترین مجموعه موجود را به عنوان مجموعه مرجع در نظر بگیرید. وقتی صحبت از اعداد باشد بزرگترین مجموعه ممکن همان \(\mathbb{R}\) است.
مثال
1 متمم هر یک از مجموعه های زیر را بنویسید.
الف \(A = \{ 1,3,5,...\} ,U = \mathbb{N}\)
\(A' = \{ 2,4,6,...\} \)
ب \(B = \mathbb{N},U = \mathbb{Z}\)
\(B' = \{ ..., - 2, - 1,0\} \)
2 اگر U مجموعه مرجع دلخواهی باشد و \(A \subseteq U\) باشند طرف دوم تساوی های زیر را بنویسید.
الف \(A \cup A' = \)
\(A \cup A' = U\)
ب \(A \cap A' = \)
\(A \cap A' = \emptyset \)
تعداد اعضای اجتماع دو مجموعه
فرض کنید تعداد اعضای مجموعه های A ,B معلوم باشد. می خواهیم تعداد اعضای مجموعه \(A \cup B\) را بر حسب \(n(A)\) و \(n\left( B \right)\) بیابیم. (تعداد اعضای یک مجموعه را هم با نماد \(\left| A \right|\) و هم با نماد \(n(A)\)نشان می دهند) ممکن است تصور کنید که جواب واضح است و برابر است با عدد \(n\left( A \right) + n\left( B \right)\) اما این نادرست است، چرا که اگر \(U = \mathbb{N},A = \{ 1,2,3\} ,B = \{ 2,3,4\} \) آنگاه:
\(4 = n\left( {A \cup B} \right) \ne n\left( A \right) + n\left( B \right) = 3 + 3 = 6\)
دلیل آن ها ساده است. هنگامی که می نویسیم \(n\left( A \right) + n\left( B \right)\) در واقع اعضای مشترک دوبار شمارش شده اند. یعنی \(n\left( {A \cap B} \right)\) یکبار در هنگام شمارش اعضای A و یک بار در شمارش اعضای B حساب شده است. لذا برای یافتن تعداد درست باید یکبار \(n(A \cap B)\) را از \(n\left( A \right) + n\left( B \right)\) کم کنیم. پس جواب درست بصورت زیر است:
\(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\)
به شکل زیر دقت کنید. می توان درستی رابطه فوق را از روی نمودار ون زیر تحقیق کرد.
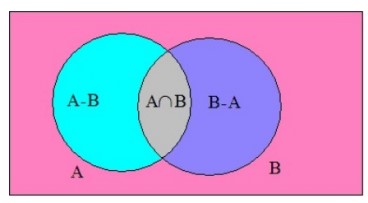
از روی شکل فوق روابط جالب دیگری بین اعضای مجموعه های \(A - B\) و \(A \cap B\) به دست می آید. این روابط به صورت زیر هستند:
\(\begin{array}{l}n\left( {A - B} \right) + n\left( {A \cap B} \right) + n\left( {B - A} \right) = n\left( {A \cup B} \right)\\n\left( {A - B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\\n\left( {B - A} \right) = n\left( B \right) - n\left( {A \cap B} \right)\end{array}\)
1 در یک کلاس مدرسه ٣٠ دانش آموز وجود دارد. ٢٢ نفر از آنها فوتبال بازی می کنند و ١٨ نفر هم والیبال بازی می کنند. چند نفر هم فوتبال بازی می کنند و هم والیبال؟
\(\begin{array}{l}n\left( F \right) = 22\\n\left( V \right) = 18\\n\left( {F \cup V} \right) = 30\\n\left( {F \cap V} \right) = ?\\n\left( {F \cup V} \right) = n\left( F \right) + n\left( V \right) - n\left( {F \cap V} \right)\\30 = 22 + 18 - n\left( {F \cap V} \right) \to n\left( {F \cap V} \right) = 10\end{array}\)
2 از بین اعداد ١ تا ٢٠٠ چند عدد وجود دارد که بر ۵ یا ٧ بخش پذیر باشد؟
\(\begin{array}{l}n\left( 5 \right) = 40\\n\left( 7 \right) = 28\\n\left( {35} \right) = 5\\n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\\ \to n\left( {A \cup B} \right) = 40 + 28 - 5 = 63\\ \to n\left( {A \cup B} \right) = 63\end{array}\)
الف چند عدد بر ۵ بخش پذیر است اما بر ٧ بخش پذیر نیست؟
\(\begin{array}{l}n\left( {A - B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\\ \to n\left( {5 - 7} \right) = 40 - 5 = 35 \to n\left( {5 - 7} \right) = 35\end{array}\)
3 در يک کلاس ٣٠ نفری، ٢١ نفر به زبان انگليسی، ١٧ نفر به زبان فرانسه و ١٠ نفر به هـر دو زبان می توانند صحبت کنند. در اين کلاس چند نفر هستند که به هيچ يک از ايـن دو زبـان صـحبت نمی کنند؟
\(\begin{array}{l}n\left( U \right) = 30\\n\left( E \right) = 21\\n\left( F \right) = 17\\n\left( {E \cap F} \right) = 10\\n\left( {E \cup F} \right) = n\left( E \right) + n\left( F \right) - n\left( {E \cap F} \right)\\n\left( {E \cup F} \right) = 21 + 17 - 10 = 28 \to n\left( {E \cup F} \right) = 28\\n\left( U \right) - n\left( {E \cup F} \right) \to 30 - 28 = 2\end{array}\)
4 در یک نظرسنجی از ١١٠ مشتری یک فروشگاه زنجیره ای مشخص شد که ٧٠ نفر آنها در یک ماه گذشته از محصولات شرکت A و ۵٧ نفرشان از محصولات شرکت B خرید کرده اند. همچنین ٣٢ نفر از آنان نیز اعلام کردند که در این مدت از هر دو شرکت خرید داشته اند. چه تعداد از این ١١٠ نفر در یک ماه گذشته :
الف دست کم از یکی از این دو شرکت خرید داشته باشند؟
\(\begin{array}{l}n\left( A \right) = 70\\n\left( B \right) = 57\\n\left( {A \cap B} \right) = 32\\n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\\n\left( {A \cup B} \right) = 70 + 57 - 32 \to n\left( {A \cup B} \right) = 95\end{array}\)
ب فقط از شرکت A خرید داشته اند.
\(\begin{array}{l}n\left( {A - B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\\n\left( {A - B} \right) = 70 - 32 \to n\left( {A - B} \right) = 38\end{array}\)
پ دقیقاً از یکی از این دو شرکت خرید داشته اند.
\(\begin{array}{l}n\left( {B - A} \right) = n\left( B \right) - n\left( {A \cap B} \right)\\n\left( {B - A} \right) = 57 - 32\\n\left( {B - A} \right) = 25\\n\left( {A - B} \right) = 38\\25 + 38 = 63\end{array}\)
تهیه کننده: فرهاد صمدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
الگو ها
الگو
دنیای اطراف ما سرشار از الگوهای مختلفی است. به عنوان نمونه، پیدایش شبانه روز و تغییر فصول مختلف سال جلوه ای از الگوی حاکم بر طبیعت است. از سوی دیگر نظم و قانونمندی های موجود در یک الگو به خودی خود برای ما جذاب است. چه بسا ممکن است طرح های روی یک گل آفتابگردان، شکل های هندسی روی یک سطح کاشی کاری شده و یا مارپیچ های روی میوه آناناس توجه شما را به خود جلب کرده باشند. به طور کلی می توان گفت الگو یک ساختار منظم از اشکال، تصاویر، صداها، نمادها، وقایع و یا اعداد می باشد که ممکن است تکرار شونده یا رشد کننده و یا ترکیبی از این دو باشد. ریاضیات به عنوان ملکه علوم، یکی از رسالت های مهم خود را مدل سازی کردن پدیده های طبیعی و پی بردن به الگوهای نهفته در آنها می داند. اهمیت این موضوع به قدری است که برخی از ریاضیدانان معتقدند که ریاضی عبارتست از علم مطالعه الگوها. در این بخش برخی الگوهای هندسی و نیز الگوهای عددی متناظر با آنها مورد بررسی قرار می گیرند.
به شکل زیر دقت کنید در هر مورد ارتباطی بین a و b و c وجود دارد:

همانطور که در شکل بالا دیده شد اختلاف هر جمله از جمله قبلی مقدار ثابتی است. این نوع الگو ها را الگوی خطی می نامیم چرا که به شکل معادله درجه اول \({t_n} = an + b\) در اینجا \({t_n}\) جمله nام الگو است.
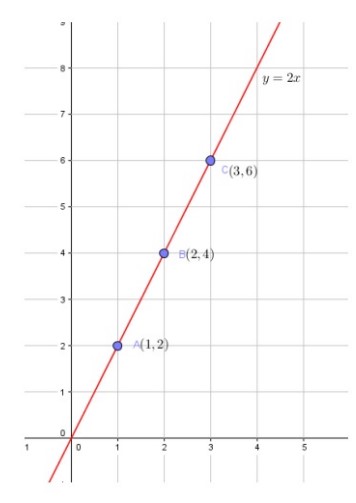
نمودار یک الگوی خطی
همانطور که در شکل بالا مشاهده می کنید اعضای دنباله ی \(2,4,6,...\) در واقع عرض نقاط \(A,B,C,...\) روی خط \(y = 2x\) هستند. به همین علت هم به این الگوها خطی گویند. اگر خوب به معادله آن که بر حسب متغبر n نوشته شده است دقت کنید بلافاصله به یاد معادله خط ار کلاس نهم خواهید افتاد یعنی عبارت \(y = ax + b\) اما همه ی الگوها لزوما خطی نیستند.
الف جمله ی عمومی الگوی زیر را با توجه به تعداد مربع ها به دست آورید.
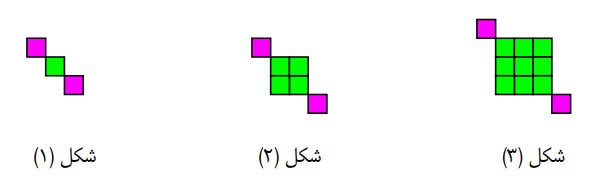
\(\begin{array}{l}{a_1} = {\left( 1 \right)^2} + 2\\{a_2} = {\left( 2 \right)^2} + 2\\{a_n} = {n^2} + 2\end{array}\)
ب آیا این یک الگوی خطی است؟
چون جمله ی عمومی اين الگو به صورت \(y = ax + b\) نیست، پس این الگو خطی نمی باشد.
تهیه کننده: فرهاد صمدی
جزوات جامع پایه دهم
جزوه جامع ریاضی دهم فصل 1 مجموعه، الگو و دنباله
جزوه جامع ریاضی دهم فصل 2 مثلثات
جزوه جامع ریاضی دهم فصل 3 توان های گویا و عبارت های جبری
جزوه جامع ریاضی دهم فصل 4 معادله ها و نامعادله ها
جزوه جامع ریاضی دهم فصل 5 تابع
جزوه جامع ریاضی دهم فصل 6 شمارش، بدون شمردن
جزوه جامع ریاضی دهم فصل 7 آمار و احتمال
دنباله ها
دنباله
به هر تعداد از اعداد که آنها را پشت سر هم نوشته باشیم یک دنباله گوییم. هر عدد که در دنباله قرار دارد را یک عضو دنباله گوییم و جمله n ام یا جمله عمومی دنباله را با نماد \({a_n}\) نمایش می دهیم. نماد رایج برای نوشتن جمله عمومی یک دنباله نماد \(\{ \} \) است. مثلا می نویسیم \({a_n} = \frac{{{n^2} + 1}}{{5n}}\) یا معادلا عبارت \(\{ \frac{{{n^2} + 1}}{{5n}}\} \) .
مثال
پنج جمله اول دنباله های زیر را بنویسید.
الف \({a_n} = {\left( { - 1} \right)^n}{2^n}\)
\(\begin{array}{l}n = 1\\{a_1} = {\left( { - 1} \right)^1}{2^1} \to {a_1} = - 2\\n = 2\\{a_2} = {\left( { - 1} \right)^2}{2^2} \to {a_2} = 4\\n = 3\\{a_3} = {\left( { - 1} \right)^3}{2^3} \to {a_3} = - 8\\n = 4\\{a_4} = {\left( { - 1} \right)^4}{2^4} \to {a_4} = 16\\n = 5\\{a_5} = {\left( { - 1} \right)^5}{2^5} \to {a_5} = - 32\end{array}\)
ب \({b_n} = {\left( {\frac{1}{3}} \right)^n}\)
\(\begin{array}{l}n = 1\\{b_1} = {\left( {\frac{1}{3}} \right)^1} \to {b_1} = \frac{1}{3}\\n = 2\\{b_2} = {\left( {\frac{1}{3}} \right)^2} \to {b_2} = \frac{1}{9}\\n = 3\\{b_3} = {\left( {\frac{1}{3}} \right)^3} \to {b_3} = \frac{1}{{27}}\\n = 4\\{b_4} = {\left( {\frac{1}{3}} \right)^4} \to {b_4} = \frac{1}{{81}}\\n = 5\\{b_5} = {\left( {\frac{1}{3}} \right)^5} \to {b_5} = \frac{1}{{243}}\end{array}\)
دنباله حسابی
دنباله ای که در آن هر جمله (به جز جمله اول) با اضافه شدن عددی ثابت به جمله قبل از خودش به دست می آید، یک دنباله حسابی نامیده می شود و به آن عدد ثابت، قدر نسبت دنباله می گویند. فرض کنید جمله اول دنباله a و قدر نسبت عدد d باشد در این صورت جملات ابتدایی دنباله بصورت زیر است:
\(a,a + d,a + 2d,a + 3d,...,a + \left( {n - 1} \right)d\)
به این ترتیب جمله عمومی دنباله حسابی بصورت زیر حاصل می شود:
\({a_n} = {a_1} + \left( {n - 1} \right)d\)
مثال
در یک دنباله حسابی داریم \({a_{11}} = 48\) و \({a_5} = 24\) مطلوبست محاسبه \({a_{20}}\) .
\(\begin{array}{l}{a_n} = {a_1} + \left( {n - 1} \right)d\\{a_{11}} = {a_1} + 10d \to {a_1} + 10d = 48\\{a_5} = {a_1} + 4d \to {a_1} + 4d = 28\\d = \frac{{10}}{3},{a_1} = \frac{{44}}{3}\\{a_{20}} = \frac{{44}}{3} + \left( {19} \right)\frac{{10}}{3} \to {a_{20}} = 78\end{array}\)
برای پیدا کردن مجموع n جمله اول یک دنباله حسابی را به دست آوریم از فرمول زیر استفاده می کنیم:
\({S_n} = \frac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]\)
دنباله هندسی
دنباله هندسی، دنباله ای است که در آن هر جمله (به جز جمله اول) از ضرب جمله قبل از خودش در عددی ثابت به دست می آید. این عدد ثابت را قدرنسبت دنباله می نامیم. جمله اول دنباله هندسی \(a \ne 0\) است. قدر نسبت را با q نشان می دهیم. در حالت های خاص اگر \(q = 0\) یا \(q = 1\) باشد، دنباله های خاصی پدید می آیند.
اگر \(q = 0\) باشد دنباله به صورت \(a,0,0,0,...\) و اگر \(q = 1\) دنباله ثابت \(a,a,a,...\) حاصل می شوند.
برای یافتن جمله عمومی یک دنباله هندسی فرض می کنیم جمله اول آن a و قدرنسبت q باشد در این صورت ترتیب جملات بصورت زیر است:
\(a,aq,a{q^2},...,a{q^{n - 1}}\)
بنابراین جمله n ام یا جمله عمومی دنباله هندسی بصورت زیر حاصل می شود:
\({a_n} = {a_1}{q^{n - 1}}\)
در یک دنباله هندسی که جمله اول آن مثبت است چنانچه \(q\rangle 1\) باشد دنباله افزایشی است و اگر \(0\langle q\langle 1\) باشد دنباله کاهشی است. اگر \(q = - 1\) باشد دنباله متناوب است و اگر \(q\langle 0\) باشد، دنباله نوسانی است.
1 اگر تعداد زیر مجموعه های یک مجموعه \(k + 1\) عضوی 24 واحد کم تر از تعداد زیر مجموعه های یک مجموعه \(k + 3\) عضوی باشد، آنگاه k را بیابید.
\(\begin{array}{l}{2^{k + 1}} = {2^{k + 3}} - 24 \to {2^{k + 3}} - {2^{k + 1}} = 24 \to {2^k}\left( {8 - 2} \right) = 24\\{2^k} = 4 \to k = 2\end{array}\)
2 اگر جمله چهارم یک دنباله هندسی 1 و جمله ی هفتم آن 8 باشد، آنگاه جمله عمومی این دنباله را بیابید.
\(\begin{array}{l}{a_n} = {a_1}{q^{n - 1}}\\{a_1}{q^3} = 1\\{a_1}{q^6} = 8\\ \to \frac{{{a_1}{q^6}}}{{{a_1}{q^3}}} = \frac{8}{1} \to {q^3} = 8 \to q = 2\\{a_1}{q^3} = 1 \to {a_1}{2^3} = 1 \to {a_1} = \frac{1}{8}\\{a_n} = {a_1}{q^{n - 1}} = \left( {\frac{1}{8}} \right)\left( {{2^{n - 1}}} \right) = \frac{1}{{{2^3}}} \times {2^{n - 1}} \to {a_n} = {2^{n - 4}}\end{array}\)
3 اگر در یک دنباله ی حسابی جمله ی چهارم برابر \(-8\) باشد، مجموع جملات اول، سوم، پنجم و هفتم چیست؟
\(\begin{array}{l}{a_1} + 3d = - 8\\{a_1} + {a_1} + 2d + {a_1} + 4d + {a_1} + 6d = 4{a_1} + 12d = 4\left( {{a_1} + 3d} \right) = 4 \times \left( { - 8} \right) = - 32\end{array}\)
تهیه کننده: فرهاد صمدی



1736019749.png)















