درسنامه کامل هندسه دهم فصل 1 ترسیم های هندسی و استدلال
تعداد بازدید : 7.59Mخلاصه نکات هندسه دهم فصل 1 ترسیم های هندسی و استدلال - درسنامه شب امتحان هندسه دهم فصل 1 ترسیم های هندسی و استدلال - جزوه شب امتحان هندسه دهم نوبت اول فصل 1 ترسیم های هندسی و استدلال
ترسیم های هندسی
ترسیم های هندسی
مجموعه همه نقاطی که از یک نقطه ثابت مانند O به فاصله معلومی مانند R هستند، دایره نامیده می شود. O را مرکز و R را شعاع دایره می نامیم.
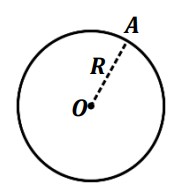
مثال
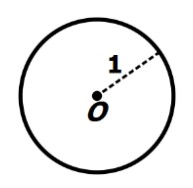
مجموعه نقاطی را مشخص کنید که فاصله آنها از یک نقطه برابر با 1 باشد.
یک نقطه ثابت مانند O را در نظر بگیرید. بینهایت نقطه در جهات مختلف O وجود دارند که فاصله آنها تا O برابر با 1 است. کافیست دهانه پرگار را به اندازه 1 باز کنیم و دایره ای به شعاع 1 و مرکز R رسم کنیم.
تعیین نقطه ای که از دو نقطه ثابت به فاصله های معلوم باشد
فرض کنیم A و B دو نقطه ثابت به فاصله a از یکدیگر باشند. برای یافتن نقطه ای که از A به فاصله ی \({d_1}\) و از B به فاصله ی \({d_2}\) باشد. دو دایره یکی به مرکز A و شعاع \({d_1}\) و دیگری به مرکز B و شعاع \({d_2}\) رسم می کنیم. نقطه یا نقاط تلاقی دو دایره جواب است. به شکل زیر توجه کنید:
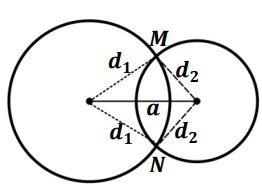
در شکل دو نقطه و از دو نقطه ثابت M و N به یک فاصله هستند.
اگر دو دایره مماس شوند مسئله یک جواب دارد.
اگر دو دایره یکدیگر را قطع نکنند، مسئله جواب ندارد.
مثال
دو نقطه ی A و B به فاصله 6 سانتی متر مفروض هستند. نقاطی را بیابید که از دو نقطه A و B به فاصله 6 سانتی متر باشند.
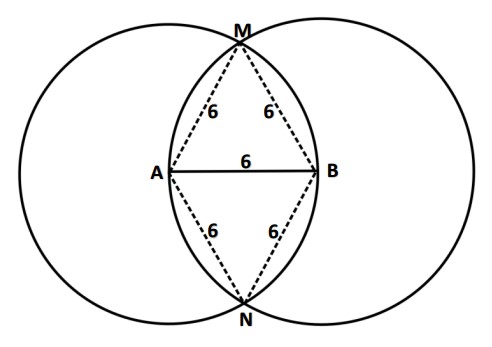
نقاط M و N جواب هستند.
رسم مثلثی که سه ضلع آن معلوم است
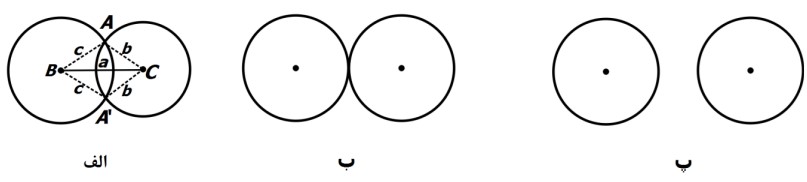
فرض کنیم سه ضلعی مثلثی a، b و c داده شده است. برای رسم مثلث، ابتدا یکی از سه ضلع داده شده مثلا بزرگ ترین ضلع را رسم می کنیم (\(BC = a\) )، سپس به مرکز B و شعاع c و به مرکز C و شعاع b دو دایره رسم می کنیم. در صورت تقاطع دو دایره، جای راس سوم مثلث یعنی نقطه A معلوم می شود.
الف) اگر دو دایره متقاطع باشند، مسئله دو جواب دارد. مثلث های \(ABC\) و \(A'BC\) که با یکدیگر به حالت (ض ض ض) هم نهشت اند.
ب) اگر دو دایره مماس باشند، در اینصورت مسئله جواب ندارد.
تهیه کننده: پریسا استواری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
زاویه
زاویه
دو نیم خط با ابتدای مشترک تشکیل یک زاویه می دهند. پس برای رسم یک زاویه کافیست با استفاده از خط کش دو نیم خط متقاطع رسم کنیم.
برخی خواص نیمساز یک زاویه
الف) اگر نقطه ای روی نیم ساز یک زاویه باشد، از دو ضلع آن زاویه به یک فاصله است. یعنی در شکل زیر داریم:
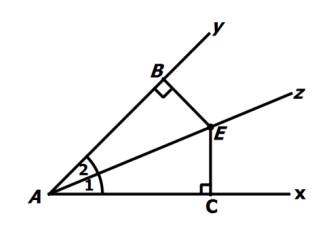
\(BE = CE\)
منظور از فاصله، کوتاه ترین فاصله است که همان فاصله عمودی می باشند.
ب) اگر نقطه ای به فاصله یکسان از دو ضلع یک زاویه باشد، آن نقطه روی نیمساز آن زاویه قرار دارد. یعنی در شکل زیر، با فرض \(BE = CE\) ، داریم \({\hat A_1} = {\hat A_2}\) .
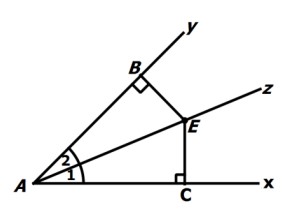
رسم نیمساز یک زاویه
الف) دهانه پرگار را کمی باز کنید و به مرکز A کمانی بزنید تا نیم خط \(AX\) و \(AY\) را در نقطه C و B قطع کند، داریم \(AB = AC\) .
ب) به مرکز C و شعاع BC و بار دیگر به مرکز B و شعاع BC دو کمان رسم می کنیم. نقطه تلاقی این دو کمان را E می نامیم. داریم \(CE = BE\) .
پ) AE نیم ساز زاویه XAY است. زیرا دو مثلث ABE و ACE به حالت (ض ض ض) هم نهشت اند. پس \({\hat A_1} = {\hat A_2}\) .
مثال
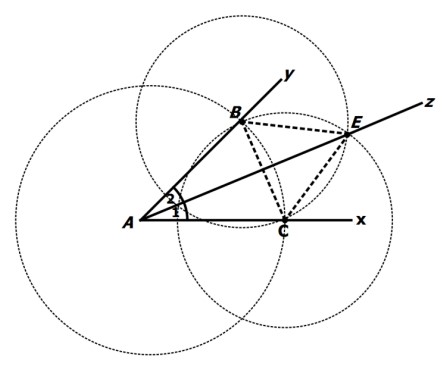
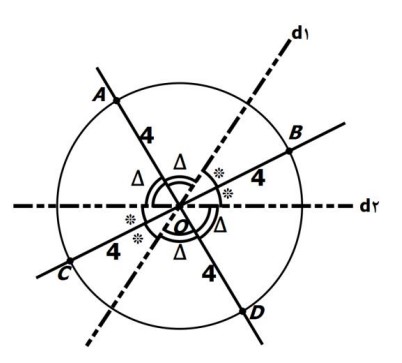
دو خط متقاطع \({d_1}\) و \({d_2}\) مفروضند. نقطه ای بیابید که از نقطه تقاطع دو خط به فاصله 4 سانتی متر باشد و از هر یک از دو خط \({d_1}\) و \({d_2}\) به یک فاصله باشد.
نقطه ای که از دو خط متقاطع \({d_1}\) و \({d_2}\) به یک فاصله قرار دارد روی نیمساز زوایای ایجاد شده بین دو خط است. از طرفی نقطه ای که از نقطه O (محل تلاقی دو خط) به فاصله 4 سانتی متر است روی دایره ای به مرکز O و شعاع 4 سانتی متر قرار دارد، پس محل تلاقی این دایره با نیمسازها جواب است، یعنی \(D,C,B,A\) .
تمام نقاط روی نیمساز یک زاویه، از دو ضلع زاویه به یک فاصله اند.
قضیه 1
نشان دهید که تمام نقاط روی نیمساز یک زاویه، از دو ضلع زاویه به یک فاصله اند.
اثبات
زاویه ی O و نقطه ی A روی نیم ساز O را در نظر بگیرید. می دانیم که فاصله ی یک نقطه از یک خط برابر است با طول پاره خط عمود بر آن؛ بنابراین از نقطه A به اضلاع زاویه ی O عمود می کنیم و نقاط تقاطع را E و F می نامیم. دو مثلث OAE و OAF را در نظر بگیرید. داریم:
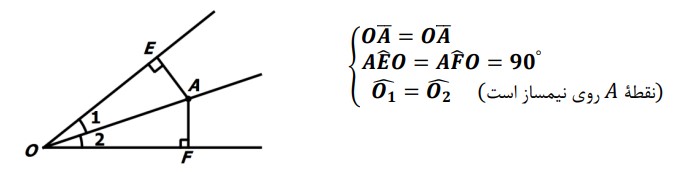
بنابراین دو مثلث OAE و OAF بنابر حالت وتر و یک زاویه حاده همنهشت هستند. یعنی
\(\Delta AEO \cong \Delta AFO\)
در نتیجه \(AE = AF\) ؛ یعنی فاصله تمام نقاط روی نیمساز یک زاویه از دو ضلع زاویه به یک اندازه اند.
اگر نقطه ای از دو ضلع یک زاویه به یک فاصله باشد آنگاه حتماً روی نیمساز زاویه قرار دارد.
قضیه 2
نشان دهید که اگر نقطه ای از دو ضلع یک زاویه به یک فاصله باشد آنگاه حتماً روی نیمساز زاویه قرار دارد.
اثبات
نقطه A را داخل زاویه O طوری در نظر بگیرید که فاصله اش تا دو ضلع زاویه مقداری یکسان باشد. A را به O وصل می کنیم. دو مثلث OAE و OAF را در نظر بگیرید. داریم:
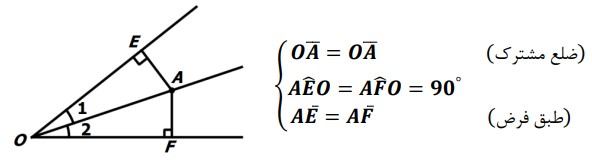
بنابراین دو مثلث OAE و OAF بنابر حالت وتر و یک ضلع همنهشت هستند؛ یعنی:
\(\Delta AEO \cong \Delta AFO\)
در نتیجه \({\hat O_1} = {\hat O_2}\) ؛ یعنی اگر نقطه ای از دو ضلع یک زاویه به یک فاصله باشد آنگاه حتماً روی نیمساز زاویه قرار دارد.
تهیه کننده: پریسا استواری
جزوات جامع پایه دهم
جزوه جامع هندسه دهم فصل 1 ترسیم های هندسی و استدلال
جزوه جامع هندسه دهم فصل 2 قضیۀ تالس، تشابه و کاربردهای آن
جزوه جامع هندسه دهم فصل 3 چند ضلعی ها
جزوه جامع هندسه دهم فصل 4 تجسم فضایی
عمود منصف
عمود منصف
خطی است که بر پاره خط عمود است و آن را نصف می کند.
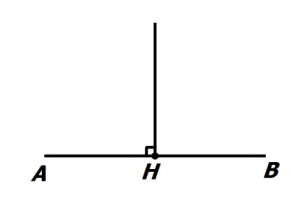
برخی خواص عمود منصف یک پاره خط
الف) اگر نقطه ای روی عمود منصف یک پاره خط باشد، از دو سر آن پاره خط به یک فاصله است. یعنی در شکل زیر داریم:
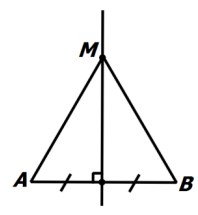
\(AM = BM\)
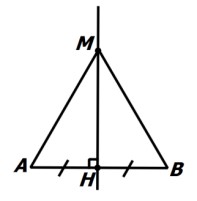
ب) اگر نقطه ای از دو سر یک پاره خط به یک فاصله باشد، روی عمودمنصف آن پاره خط قرار دارد. یعنی در شکل زیر، با فرض \(AM = BM\) ، داریم \(AH = BH\) و \(MH \bot AB\) .
تهیه کننده: پریسا استواری
رسم عمود منصف یک پاره خط
رسم عمود منصف یک پاره خط
پاره خط AB مفروض است.
دهانه پرگار را بیش از نصف طول AB باز می کنیم و یکبار کمانی به مرکز A و بار دیگر با همان اندازه از نقطه B کمان بزنید تا یکدیگر را در دو نقطه M و N قطع کنند. داریم:
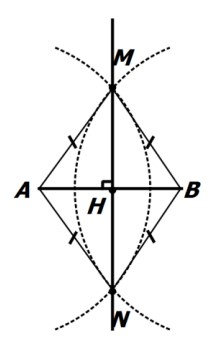
\(AM = BM,AN = BN\)
زیرا اندازه شعاع دایره ثابت است.
خط MN عمود منصف پاره خط AB است، زیرا M و N از دو سر پاره خط AB به یک فاصله اند و \(MN \bot AB\) .
اگر نقطه ای روی عمود منصف یک پاره خط باشد، فاصله اش از دوسر پاره خط به یک اندازه است.
قضیه 3
نشان دهید که اگر نقطه ای روی عمود منصف یک پاره خط باشد، فاصله اش از دوسر پاره خط به یک اندازه است.
اثبات
پاره خط AB و عمود منصف MH و نقطه P روی آن را در نظر بگیرید. نقطه P را به A و B وصل می کنیم. داریم:
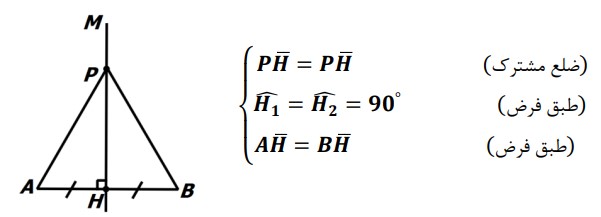
بنابراین دو مثلث PHA و PHB بنابر حالت دو ضلع و زاویه بین همنهشت هستند. یعنی:
\(\Delta PHA \cong \Delta PHB\)
در نتیجه \(AP = BP\) .
اگر نقطه ای فاصله اش تا دو سر یک پاره خط به یک اندازه باشد، آنگاه آن نقطه روی عمود منصف پاره خط است.
قضیه 4
نشان دهید که اگر نقطه ای فاصله اش تا دو سر یک پاره خط به یک اندازه باشد، آنگاه آن نقطه روی عمود منصف پاره خط است.
اثبات
پاره خط AB و نقطه P روی آن را در نظر بگیرید؛ به طوری که فاصله P تا دو سر پاره خط AB به یک اندازه باشد. یعنی:
\(AP = BP\)
از نقطه P به AB عمود می کنیم و پای عمود را H می نامیم. داریم:
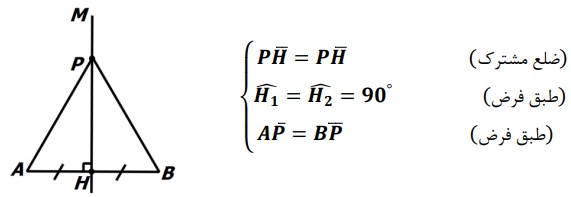
بنابراین دو مثلث PHA و PHB بنابر حالت وتر و یک ضلع همنهشت هستند. یعنی:
\(\Delta PHA \cong \Delta PHB\)
در نتیجه \(AH = BH\) ، پس P روی عمود منصف AB قرار دارد.
تهیه کننده: پریسا استواری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
رسم خط عمود بر یک خط از نقطه ای روی آن
رسم خط عمود بر یک خط از نقطه ای روی آن
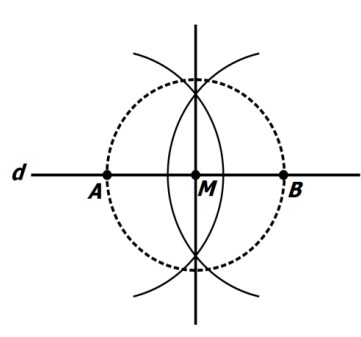
خط d و نقطه ی M را روی آن در نظر بگیرید.
دایره ای به مرکز M و شعاع دلخواه رسم کنید.
نقاط برخورد را A و B بنامید.
عمود منصف پاره خط AB را رسم کنید.
در این صورت خطی عمود بر خط d رسم کرده ایم که از نقطه M می گذرد.
رسم خط عمود بر یک خط از نقطه ای غیر واقع بر آن
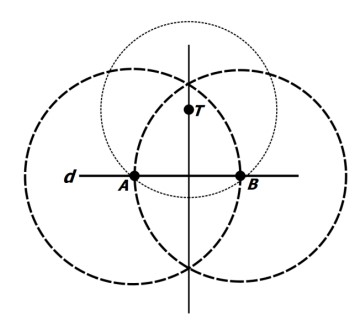
خط d و نقطه ی T را روی آن در نظر بگیرید.
دهانه ی پرگار را بیشتر از فاصله ی T تا خط d باز کرده و دایره ای به مرکز T رسم کنید.
نقاط برخورد را A و B بنامید.
عمود منصف پاره خط AB را رسم کنید.
نقطه T از نقاط A و B به یک فاصله است، بنابراین T روی عمود منصف پاره خط AB و در نتیجه روی خط عمود بر خط d قرار دارد.
رسم خط موازی با یک خط از یک نقطه غیر واقع بر آن
خط d و نقطه p خارج از آن را در نظر بگیرید:
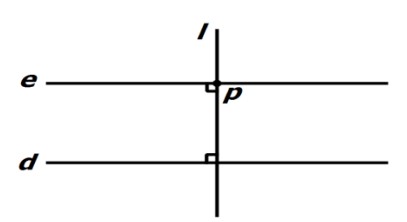
خط عمود بر d و گذرنده از نقطه p را رسم کنید، آن را L می نامیم.
خط عمود بر L و گذرنده از نقطه e را رسم کنید، آن را L می نامیم.
خط L را به عنوان خط مورب گذرنده از دو خط d و e در نظر می گیریم؛ زیرا تمام زوایای حاصل با هم مساوی و برابر \({90^0}\) هستند، بنابراین خط e با خط d موازی است.
تهیه کننده: پریسا استواری
جزوات جامع پایه دهم
جزوه جامع هندسه دهم فصل 1 ترسیم های هندسی و استدلال
جزوه جامع هندسه دهم فصل 2 قضیۀ تالس، تشابه و کاربردهای آن
جزوه جامع هندسه دهم فصل 3 چند ضلعی ها
جزوه جامع هندسه دهم فصل 4 تجسم فضایی
ترسیم لوزی
ترسیم لوزی
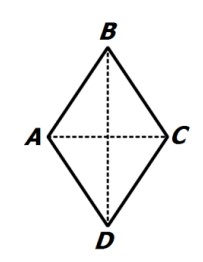
قبل از روش ترسیم، خواص لوزی را یادآوری می کنیم:
ضلع های روبرو موازی اند.
تمام اضلاع برابرند.
زوایای روبرو دو به دو برابرند.
قطر ها عمود منصف یکدیگرند.
زوایای مجاور مکمل اند.
دارای 2 محور تقارن است.
قطر ها نیمساز زاویه ها هستند.
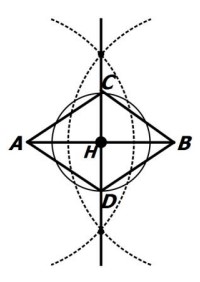
لوزی با قطرهایی به طول 6 و 4 رسم کنید.
پاره خط AB به طول 6 رسم می کنیم.
عمود منصف AB را رسم می کنیم. نقطه ی برخورد با AB را H می نامیم.
دهانه ی پرگار را به اندازه 2 باز کرده و دایره ای به مرکز H و شعاع 2 می زنیم.
نقاط برخورد با عمود منصف را C و D می نامیم، C و D را به A و B وصل می کنیم.
چون قطر ها بر هم عمود هستند و یکدیگر را نصف می کنند؛ بنابراین چهار ضلعی ABCD یک لوزی است.
تهیه کننده: پریسا استواری
یافتن مرکز دایره
یافتن مرکز دایره
قضیه 5
عمود منصف وتر یک دایره از مرکز آن می گذرد.
اثبات
دایره ای به مرکز O و وتر AB در آن در نظر بگیرید. از O به AB عمود می کنیم و نقطه برخورد را H می نامیم.
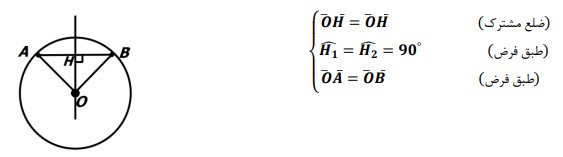
بنابراین دو مثلث OAH و OHB بنابر حالت وتر و یک ضلع همنهشت هستند. یعنی:
\(\Delta OHA \cong \Delta OHB\)
در نتیجه \(AH = BH\) ، در نتیجه عمود منصف وتر AB از O می گذرد.
پس برای یافتن مرکز یک دایره کافیست:
دو وتر از دایره را که با هم موازی نیستند رسم می کنیم.
عمود منصف های آنها را رسم می کنیم.
چون عمود منصف ها از مرکز دایره می گذرند، بنابراین محل برخورد عمود منصف های دو وتر غیرموازی در دایره، مرکز دایره است.
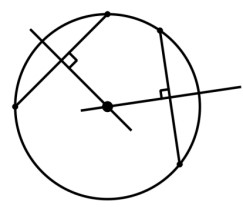
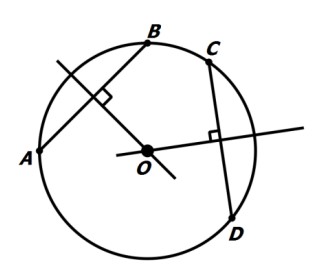
میدان یک شهر به صورت دایره است. می خواهیم مرکز آن را یافته و در آنجا مجسمه ای قرار می دهیم. به کمک وسایل ترسیم و ترسیم های مقدماتی، مرکز این دایره را بیابید.
می دانیم که مرکز دایره روی عمود منصف های وترهای آن قرار دارد. دو وتر دلخواه AB و CD را می کشیم و عمود منصف های آنها را رسم می کنیم، محل برخورد این عمود منصف ها مرکز دایره را نشان می دهد.
تهیه کننده: پریسا استواری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
استدلال
استدلال
در احکام و مسائل هندسی همواره به استدلالی نیاز است که درستی یا نادرستی هر یک را نشان می دهد.(اثبات کند) در اینگونه موارد، معمولا به دو صورت با مسأله برخورد می شود.
استدلال استقرایی
در این روش با چندین مشاهده، یک نتیجه گیری کلی انجام می دهیم. یعنی:
استدلال استقرایی رسیدن از جزء به کل است.
مثال
یک انسان دوره ماقبل تاریخ را در نظر بگیرید. او ممکن است بعد از کشف آتش، این تجربیات را داشته باشد:
با حرارت دادن آب، ببینید پس از مدتی آب به بخار تبدیل می شود.
با حرارت دادن یک تکه یخ، آن هم به بخار تبدیل شده است.
و به علت دانش و اطلاعات ناقص، نتیجه گرفته باشد که:
هر شیء با حرارت دیدن، بعد از مدتی به بخار تبدیل می شود.
می دانیم که این نتیجه برای تمام اشیاء صحیح نیست و در نتیجه استدلال استقرایی ممکن است نتایج نادرست حاصل کند.
استدلال استنتاجی
برخورد صحیح با یک حکم این است:
بر اساس نتیجه گیری منطقی بر پایه واقعیت هایی است که درستی آنها را پذیرفته ایم و به آن (استدلال استنتاجی) می گویند. بنابراین استدلال استنتاجی رسیدن از کل به جزء است.
مثال نقض
اگر یک حکم نادرست باشد، کافی است یک مثال بیاوریم که نادرست بودن آن را نشان دهد. به چنین مثالی (مثال نقض) گفته می شود.
1 نشان دهید مجموع زوایای داخلی هر چهار ضلعی محدب \({360^0}\) است.
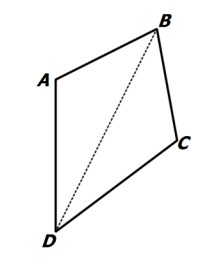
میدانیم مجموع زوایای داخلی هر مثلث \({180^0}\) است. یک چهارضلعی دلخواه مانند ABCD در نظر می گیریم و دو رأس مقابل آن را به هم وصل می کنیم. مجموع زوایای داخلی چهارضلعی ABCD با مجموع زاویه های داخلی دو مثلث ABD و BCD برابر است.
بنابراین مجموع زاویه های داخلی چهارضلعی ABCD برابر است با \({360^0}\) .
2 برای موارد زیر مثال نقض آورده و آنها را رد کنید.
الف) اگر \({x^2}\rangle 4\) باشد، در این صورت \(x\rangle 2\) است.
عدد \(x = - 3\) را در نظر بگیرید. مشاهده می کنید که \({\left( { - 3} \right)^2} = 9\rangle 4\) صحیح بوده ولی \( - 3\) بزرگتر از 2 نیست و بنابراین حکم نادرست است.
ب) نقطه همرسی ارتفاع های مثلث همیشه درون آن قرار می گیرد.
کافی است مثلثی با یک زاویه ی باز را به عنوان مثال نقض در نظر بگیرید. زیرا نقطه همرسی ارتفاع ها خارج مثلث قرار می گیرد.
تهیه کننده: پریسا استواری
جزوات جامع پایه دهم
جزوه جامع هندسه دهم فصل 1 ترسیم های هندسی و استدلال
جزوه جامع هندسه دهم فصل 2 قضیۀ تالس، تشابه و کاربردهای آن
جزوه جامع هندسه دهم فصل 3 چند ضلعی ها
جزوه جامع هندسه دهم فصل 4 تجسم فضایی
خطوط همرس
خطوط همرس
چند خط که همگی در یک نقطه مانند A مشترک باشند را همرس گویند. نقطه A را نقطه همرسی این خط ها می نامیم.
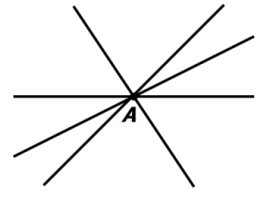
نقطه ی همرسی سه نیمساز زوایای داخلی، نقطه ای چون O درون مثلث است با این خاصیت که:
فاصله O تا سه ضلع مثلث باهم برابر است:
\(OH = OK = OL\)
اگر دهانه ی پرگار را به اندازه ی OH باز کرده و به مرکز O دایره ای رسم کنیم، این دایره از نقاط H، K و L عبور خواهد کرد.
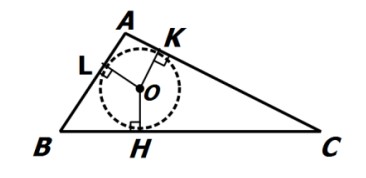
این دایره از داخل مثلث بر هر سه ضلع آن مماس است.
نقطه ی همرسی سه عمودمنصف اضلاع مثلث، نقطه ای چون O درون مثلث است.
اگر دهانه ی پرگار را به اندازه ی OA باز کرده و به مرکز O دایره ای رسم کنیم، این دایره از هر سه رأس مثلث عبور خواهد کرد:
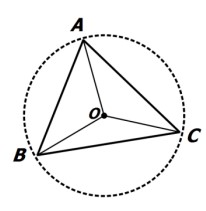
بر خلاف نقطه همرسی نیمسازهای مثلث که همیشه درون مثلث قراردارد، نقطه همرسی ارتفاع ها و عمود منصف های اضلاع ممکن است بیرون مثلث قرار گیرند.
نشان دهید نیمسازهای زوایای داخلی هر مثلث همرس اند.
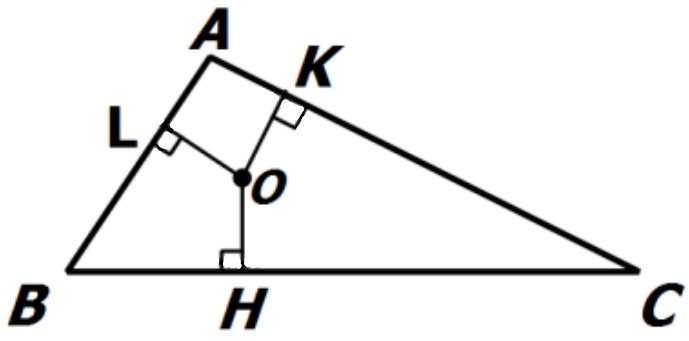
مثلث دلخواه ABC را در نظر گرفته، نیمسازهای زوایای \(\hat A\) و \(\hat B\) را رسم کرده و نقطه تقاطع آنها را O می نامیم.
همچنین با رسم عمودهایی از O بر اضلاع، فاصله O تا سه ضلع به صورت OH، OK و OL مشخص می شوند.
چون O نیم ساز زاویه \(\hat A\) است، طبق خاصیت نیمساز داریم:
\(OK = OL\)
چون O نیم ساز زاویه \(\hat B\) است، طبق خاصیت نیمساز داریم:
\(OH = OL\)
با مقایسه دو تساوی فوق نتیجه می گیریم که \(OK = OH\) ؛ یعنی فاصله O تا دو ضلع زاویه \(\hat C\) نیز باهم برابر است و در نتیجه:
نقطه O روی نیم ساز \(\hat C\) نیز قرار داشته و سه نیمساز در نقطه O همرس هستند.
تهیه کننده: پریسا استواری
قضیه و گزاره
قضیه و گزاره
گزاره
در ریاضیات، به هر ادعا یا خبر که یا (دقیقاً درست) و یا (دقیقاً نادرست) است، یک گزاره گویند.
اگر گزاره فقط شامل یک خبر باشد، به آن یک گزاره ی ساده گوئیم.
مانند: 7 چهارمین عدد اول است، یک گزاره ساده است.
اگر گزاره شامل دو یا چند خبر باشد، به آن گزاره ی (مرکب) گویند.
مانند: عدد 7 چهارمین عدد اول و عدد \(\sqrt 2 \) گنگ است، یک گزاره ی مرکب است.
در برخورد با یک گزاره، باید یکی از دو حالت زیر در نظر گرفته شود:
الف) اگر گزاره درست باشد، باید آن را با استدلال استنتاجی ثابت کنیم که به این استدلال، (برهان) هم گفته می شود.
مانند: همرس بودن ارتفاع ها یا نیمساز های زوایای داخلی مثلث.
در بین احکام درست، برخی از آنها جایگاه خاصی دارند. در هندسه، گزاره هایی که کاربردهای زیادی داشته و برای آنها برهان درستی آورده ایم، (قضیه) نامیده می شوند. بنابراین قضیه گزاره مهمی است که همواره درست است.
ب) هرگاه گزاره نادرست باشد، باید برای آنها مثال نقض ارائه دهیم.
تهیه کننده: پریسا استواری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
قضیه و گزاره شرطی
قضیه و گزاره شرطی
می توان یک گزاره را به صورت زیر بیان کرد که در اینصورت به آن (گزاره شرطی) گویند.
اگر فرض، آنگاه حکم
اگر یک قضیه را به صورت شرطی بیان کنیم، به آن (قضیه شرطی) گفته می شود.
مثال
قضیه فیثاغورث را به صورت یک گزاره شرطی بنویسید.
اگر مثلث ABC قائم الزاویه باشد و ضلع های AB و AC اضلاع قائمه آن باشند، آنگاه \(B{C^2} = A{B^2} + A{C^2}\)
قضیه 6
اگر در مثلثی دو ضلع نابرابر باشند، زاویه رو به رو به ضلع بزرگتر، بزرگتر است از زاویه رو به رو به ضلع کوچکتر.
اثبات
با توجه به شکل، حکم داده شده به صورت شرطی چنین است:
اگر در مثلث ABC، \(AC\rangle AB\) باشد، آنگاه \(\hat B\rangle \hat C\) است.
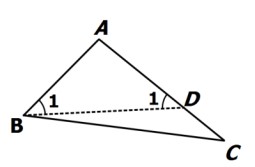
چون \(AC\rangle AB\) است، می توان نقطه D را روی ضلع AC طوری انتخاب کرد که \(AB = AD\) باشد.
بنابر انتخاب نقطه D، مثلث ABD متساوی الساقین بوده و در نتیجه \({\hat B_1} = {\hat D_1}\) است. از طرفی زاویه ی \({\hat B_1}\) جزئی از زاویه اصلی \(\hat B\) بوده و در نتیجه \(\hat B\rangle {\hat B_1}\) است. لذا:
\(\begin{array}{l}\hat B\rangle {{\hat B}_1}\\{{\hat B}_1} = {{\hat D}_1}\\ \to \hat B\rangle {{\hat D}_1}\end{array}\)
از طرف دیگر، زاویه ی \({\hat D_1}\) برای مثلث DBC یک زاویه خارجی بوده و از زاویه ی غیر مجاور خود، یعنی \(\hat C\) بزرگتر است. بنابراین:
\(\begin{array}{l}\hat B\rangle {{\hat D}_1}\\{{\hat D}_1}\rangle \hat C\\ \to \hat B\rangle \hat C\end{array}\)
تهیه کننده: پریسا استواری
جزوات جامع پایه دهم
جزوه جامع هندسه دهم فصل 1 ترسیم های هندسی و استدلال
جزوه جامع هندسه دهم فصل 2 قضیۀ تالس، تشابه و کاربردهای آن
جزوه جامع هندسه دهم فصل 3 چند ضلعی ها
جزوه جامع هندسه دهم فصل 4 تجسم فضایی
نقیض گزاره
نقیض گزاره
هر گاه در یک گزاره، خبر (حکم) آن را کاملا بر عکس کنیم، نقیض آن بدست می آید.
می توانید برای نقیض کردن گزاره، عبارت چنین نیست که را به ابتدای آن اضافه کنید.
مثال
نقیض گزاره های زیر را بنویسید.
الف امروز هوا گرم است.
چنین نیست که امروز هوا گرم است. (امروز هوا گرم است)
ب a از b بزرگتر است.
چنین نیست که a از b بزرگتر باشد.
برهان خلف
گاهی ارائه استدلال استنتاجی به صورت عادی مشکل یا غیرممکن است. در چنین صورتی، معمولا روش اثبات غیر مستقیم به صورت زیر، کمک بسیار زیادی می کند.
برای استفاده از این روش، طبق گام های زیر عمل می کنیم:
حکم مورد نظر را نادرست در نظر می گیریم؛ یعنی فرض می کنیم نقیض آن درست باشد. به این فرض جدید، (فرض خلف) هم می گویند.
با توجه به فرض مرحله ی قبل و آوردن دلیل مناسب، به یک تناقض با فرض آن قضیه یا مسأله می رسیم.
تیجه می گیریم؛ حکم آن مسئله نمی تواند نادرست باشد و از ابتدا صحیح بوده است.
از یک نقطه غیر واقع بر خط نمی توان بیش از یک عمود بر آن خط رسم کرد.
فرض: نقطه ای مانند A غیر واقع بر خطی مانند d وجود دارد.
حکم: از نقطه A نمی توان بیش از یک عمود بر خط d رسم کرد.
استدلال: با برهان خلف (برهان غیر مستقیم) فرض می کنیم حکم غلط باشد. یعنی فرض می کنیم از نقطه A د عمود بر خط d رسم کرده ایم که مانند شکل، خط d را در نقاط B و C قطع کرده اند. در این صورت مجموع زوایای داخلی مثلث ABC بزرگتر از \({180^0}\) خواهد شد و این غیر ممکن است. پس امکان رسم دو عمود از یک نقطه غیر واقع بر یک خط وجود ندارند. یعنی حکم نمی تواند غلط باشد.
تهیه کننده: پریسا استواری
عکس قضیه شرطی
عکس قضیه شرطی
برای نوشتن عکس یک قضیه شرطی، جای فرض و حکم را عوض می کنیم.
توجه کنید:
عکس یک قضیه شرطی ممکن است یک قضیه نباشد، یعنی ممکن است حکمی نادرست شود.
مثال
الف حکم زیر را به صورت شرطی نوشته و تعیین کنید درست است یا نادرست؟
در مثلث قائم الزاویه، وتر بزرگترین ضلع است.
بیان شرطی حکم با استفاده از شکل چنین است:
اگر مثلث ABC قائم الزاویه باشد \(\hat A = {90^0}\) ، آنگاه وتر BC از دو ضلع AB و AC بزرگ تر است.
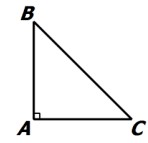
ب عکس حکم فوق را نوشته و مشخص کنید درست است یا نادرست؟
اگر در مثلث ABC ضلع BC از AB و AC بزرگتر باشد، آنگاه مثلث ABC قائم الزاویه است.
این گزاره نادرست است و می توانیم برای آن مثال نقض بیاوریم:
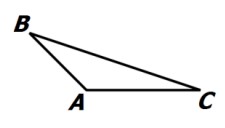
قضیه دو شرطی
هرگاه عکس یک قضیه شرطی همواره درست باشد، آن قضیه را می توان به صورت دو شرطی بیان کرد.
فرض اگر و فقط اگر حکم
1 قضیه فیثاغورث را به صورت یک قضیه دو شرطی بنویسید.
مثلث ABC قائم الزاویه است، اگر و فقط اگر \(B{C^2} = A{B^2} + A{C^2}\) .
2 عکس قضیه زیر را بنویسید.
اگر در یک چهار ضلعی متوازی الاضلاع باشد، آنگاه قطرهایش یکدیگر را نصف می کنند.
اگر در یک چهارضلعی قطرها یکدیگر را نصف کنند، آنگاه آن چهارضلعی متوازی الاضلاع است.
تهیه کننده: پریسا استواری
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم



1736019749.png)















