جواب تمرین صفحه 45 درس 2 ریاضی یازدهم تجربی (هندسه)
تعداد بازدید : 86.59Mپاسخ تمرین صفحه 45 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 45 درس هندسه
-تمرین صفحه 45 درس 2
-شما در حال مشاهده جواب تمرین صفحه 45 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در هر قسمت تشابه مثلث ها را ثابت کنید و مقادیر x و y را مشخص نمایید.
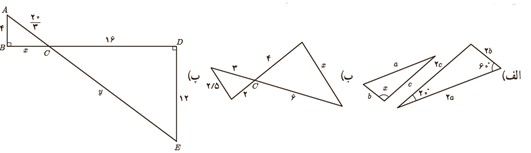
الف
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\\\\ \Rightarrow \frac{{2a}}{a} = \frac{{2b}}{b} = \frac{{2c}}{c} = 2\\\\ \Rightarrow A\mathop B\limits^\Delta C\sim A'\mathop {B'}\limits^\Delta C'\\\\ \Rightarrow x = \hat A' = \hat A\\\\ \Rightarrow x = {60^\circ } + {20^\circ } = {80^\circ }\end{array}\)
ب
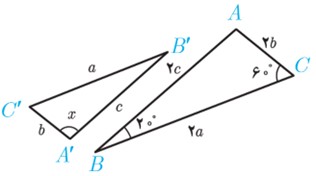
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{AC}}{{DC}} = 2\\\end{array}\\{A\hat CB = D\hat CE}\end{array}} \right. \Rightarrow A\mathop C\limits^\Delta B\sim D\mathop C\limits^\Delta E\\\\ \Rightarrow \frac{{BC}}{{EC}} = \frac{{AB}}{{DE}}\\\\ \Rightarrow \frac{x}{{2/5}} = \frac{6}{3} = 2\\\\ \Rightarrow x = 7\end{array}\)
پ
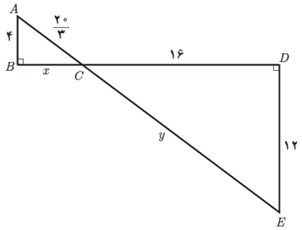
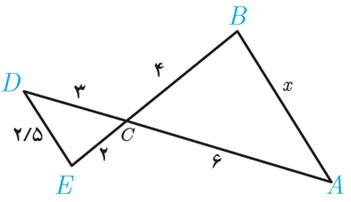
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\hat B = \hat D = {90^\circ }\\\end{array}\\{A\hat CB = D\hat CE}\end{array}} \right. \Rightarrow A\mathop C\limits^\Delta B\sim D\mathop C\limits^\Delta E\)
\(\begin{array}{l}\\ \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{CE}} = \frac{{BC}}{{CD}}\\\\ \Rightarrow \frac{4}{{12}} = \frac{{\frac{{20}}{3}}}{y} = \frac{x}{{16}}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = \frac{{16}}{3}\\\end{array}\\{y = 20}\end{array}} \right.\end{array}\)
2 در مثلث قائم الزاویهٔ روبه رو در هر حالت، اندازه پاره خط خواسته شده را به دست آورید.
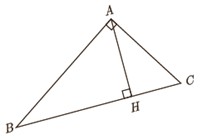
الف \(AC = ?\,,\,AB = ?\,,\,AH = ?\,,\,BH = 9\,,\,BC = 10\)
ب \(AB = ?\,,\,AH = ?\,,\,BC = ?\,,\,CH = 2\,,\,AC = 5\)
پ \(AH = ?\,,\,BC = ?\,,\,AC = 6\,,\,AB = 8\)
ت \(AC = ?\,,\,BC = ?\,,\,BH = ?\,,\,AH = 6\,,\,AB = 12\)
الف
\(\begin{array}{l}A{B^2} = BH \times BC = 9 \times 10 = 90\\\\ \Rightarrow AB = 3\sqrt {10} \\\\A{C^2} = B{C^2} - A{B^2} = 100 - 90 = 10\\\\ \Rightarrow AC = \sqrt {10} \\\\AB \times AC = AH \times BC\\\\ \Rightarrow 3\sqrt {10} \times \sqrt {10} = AH \times 10\\\\ \Rightarrow AH = 3\end{array}\)
ب
\(\begin{array}{l}A{C^2} = CH \times BC\\\\ \Rightarrow 25 = 2 \times BC\\\\ \Rightarrow BC = \frac{{25}}{2}\\\\A{B^2} = B{C^2} - A{C^2} = \frac{{625}}{4} - 25 = \frac{{525}}{4}\\\\ \Rightarrow AB = \frac{{5\sqrt {21} }}{2}\\\\AB \times AC = AH \times BC\\\\ \Rightarrow \frac{{5\sqrt {21} }}{2} \times 5 = AH \times \frac{{25}}{2}\\\\ \Rightarrow AH = \sqrt {21} \end{array}\)
پ
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = 64 + 36 = 100\\\\ \Rightarrow BC = 10\\\\AB \times AC = AH \times BC\\\\ \Rightarrow 8 \times 6 = AH \times 10\\\\ \Rightarrow AH = \frac{{48}}{{10}}\end{array}\)
ت
\(\begin{array}{l}B{H^2} = A{B^2} - A{H^2} = 144 - 36 = 108\\\\ \Rightarrow BH = 6\sqrt 3 \\\\A{B^2} = BH \times BC\\\\ \Rightarrow 144 = 6\sqrt 3 \times BC\\\\ \Rightarrow BC = 8\sqrt 3 \\\\A{C^2} = B{C^2} - A{B^2} = 192 - 144 = 48\\\\ \Rightarrow AC = 4\sqrt 3 \end{array}\)
3 شکل مقابل مستطیلی به طول 12 است. اگر از نقطهٔ A عمودی بر قطر BD رسم کنیم و پای این عمود را H بنامیم، طول BH برابر 11 است. اندازهٔ عمود رسم شده، طول قطر مستطیل و اندازهٔ عرض مستطیل را محاسبه کنید.
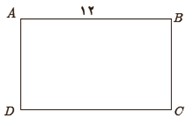
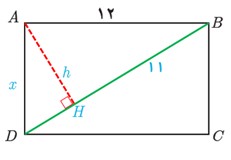
\(\begin{array}{l}A{H^2} = A{B^2} - B{H^2} = 144 - 121 = 23\\\\ \Rightarrow AH = h = \sqrt {23} \\\\A{B^2} = BH \times BD\\\\ \Rightarrow 144 = 11 \times BD\\\\ \Rightarrow BD = \frac{{144}}{{11}}\\\\AD \times AB = AH \times BD\\\\ \Rightarrow x = \frac{{\sqrt {23} \times \frac{{144}}{{11}}}}{{12}}\\\\ \Rightarrow x = \frac{{12}}{{11}}\sqrt {23} \end{array}\)
4 بر دیوار یک کمپ نظامی نورافکنی به ارتفاع 60 متر (مانند شکل) قرار گرفته است. فردی که در طرف دیگر رودخانه است، می خواهد فاصلهٔ خود را تا پایهٔ نورافکن محاسبه کند. برای این کار چوبی به طول یک متر را روی زمین قرار می دهد و مشاهده می کند که طول سایهٔ چوب برابر 5 متر است. فاصلهٔ این مرد تا پای نورافکن چقدر است؟
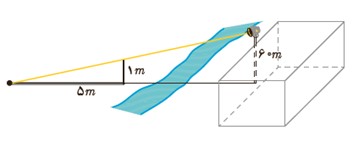
\(\left\{ {\begin{array}{*{20}{l}}{\hat A = \hat A\quad \quad \quad }\\{\hat C = \hat E = {{90}^\circ }}\end{array}} \right. \Rightarrow A\mathop B\limits^\Delta C\sim A\mathop D\limits^\Delta E\)
\(\begin{array}{l}\\ \Rightarrow \frac{{AC}}{{AE}} = \frac{{BC}}{{DE}} \Rightarrow \frac{5}{{AE}} = \frac{1}{{60}}\\\\ \Rightarrow AE = 300\\\\ \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{CE}} = \frac{{BC}}{{CD}}\\\\ \Rightarrow \frac{4}{{12}} = \frac{{\frac{{20}}{3}}}{y} = \frac{x}{{16}}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = \frac{{16}}{3}\\\end{array}\\{y = 20}\end{array}} \right.\end{array}\)
5 در شکل مقابل دو مثلث قائم الزاویه مشاهده می کنید. نسبت محیط ها و مساحت های آنها را به دست آورید.
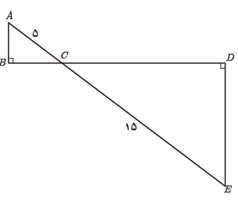
\(\left\{ {\begin{array}{*{20}{l}}{\hat B = \hat D = {{90}^\circ }}\\{A\hat CB = E\hat CD}\end{array}} \right.\,\,\,\,\, \Rightarrow A\mathop B\limits^\Delta C\sim C\mathop D\limits^\Delta E\)
\(\begin{array}{l}\\ \Rightarrow \frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} = \frac{{CE}}{{AC}} = \frac{{15}}{5} = 3\\\\\frac{{{P_{CDE}}}}{{{P_{ABC}}}} = \frac{{DC + DE + CE}}{{BC + AB + AC}} = \frac{{CE}}{{AC}}\\\\ \Rightarrow \frac{{{P_{CDE}}}}{{{P_{ABC}}}} = 3\\\\\frac{{{S_{CDE}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}DC \times DE}}{{\frac{1}{2}BC \times AB}} = \frac{{DC}}{{BC}} \times \frac{{DE}}{{AB}}\\\\ \Rightarrow \frac{{{S_{CDE}}}}{{{S_{ABC}}}} = 3 \times 3\\\\ \Rightarrow \frac{{{S_{CDE}}}}{{{S_{ABC}}}} = 9\end{array}\)
6 دو مثلث متشابه \(ABC\) و \(A'B'C'\) را با نسبت تشابه K در نظر بگیرید؛ به گونه ای که \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = K\) باشد. حال ارتفاع های \(AH\) و \(A'B'\) را در دو مثلث رسم کنید.
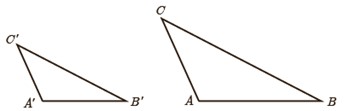
الف ثابت کنید مثلث های AHB و 'A'H'B متشابه اند.
ب نسبت \(\frac{{AH}}{{A'H'}}\) را به دست آورید.
پ نسبت مساحت های \(\frac{{{S_{ABC}}}}{{{S_{A'B'C'}}}}\) را محاسبه کنید.
ت نسبت محیط های دو مثلث ABC و 'A'B'C را به دست آورید.
الف
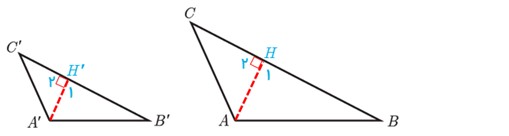
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\hat B = \hat B'\\\quad \quad \quad \end{array}\\{{{\hat H}_1} = {{\hat H'}_1} = {{90}^\circ }}\end{array}} \right. \Rightarrow A\mathop B\limits^\Delta H\sim A'\mathop {B'}\limits^\Delta H'\\\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AH}}{{A'H'}} = \frac{{CH}}{{C'H'}} = k\end{array}\)
ب
\(\frac{{AH}}{{A'H'}} = k\)
پ
\(\begin{array}{l}\frac{{{S_{ABC}}}}{{{S_{A'B'C'}}}} = \frac{{\frac{1}{2}AH \times BC}}{{\frac{1}{2}A'H' \times B'C'}} = \\\\\frac{{AH}}{{A'H'}} \times \frac{{BC}}{{B'C'}} = k \times k\\\\ \Rightarrow \frac{{{S_{ABC}}}}{{{S_{A'B'C'}}}} = {k^2}\end{array}\)
ت
\(\begin{array}{l}\frac{{{P_{ABC}}}}{{{P_{A'B'C'}}}} = \frac{{BC + AB + AC}}{{B'C' + A'B' + A'C'}} = \frac{{AC}}{{A'C'}} = k\\\\ \Rightarrow \frac{{{P_{ABC}}}}{{{P_{A'B'C'}}}} = k\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















