1736019749.png)
جواب کاردرکلاس صفحه 43 درس 2 ریاضی یازدهم تجربی (هندسه)
تعداد بازدید : 78.86Mپاسخ کاردرکلاس صفحه 43 ریاضی یازدهم تجربی
-گام به گام کاردرکلاس صفحه 43 درس هندسه
-کاردرکلاس صفحه 43 درس 2
-شما در حال مشاهده جواب کاردرکلاس صفحه 43 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 درشکل مقابل BC||DE.
اندازۀ پاره خط های DE و CA را به دست آورید.
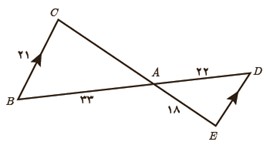
خطوط BC و ED موازی هستند و خطوط مورّب آن ها، BD و CE می باشند:
\(\begin{array}{l}\left\{ \begin{array}{l}BC\parallel ED\,\not |\,BD \Rightarrow \hat B = \hat D\\\\BC\parallel ED\,\not |\,CE \Rightarrow \hat C = \hat E\end{array} \right.\\\\ \Rightarrow A\mathop B\limits^\Delta C \sim A\mathop D\limits^\Delta E\\\\ \Rightarrow \frac{{AC}}{{AE}} = \frac{{AB}}{{AD}} = \frac{{BC}}{{DE}}\\\\ \Rightarrow \frac{{AC}}{{18}} = \frac{{33}}{{22}} = \frac{{21}}{{DE}}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\frac{{AC}}{{18}} = \frac{{33}}{{22}} \Rightarrow AC = 27\\\end{array}\\{\frac{{21}}{{DE}} = \frac{{33}}{{22}} \Rightarrow DE = 14}\end{array}} \right.\end{array}\)
2 اگر نقاط P و N و M مطابق شکل وسط های اضلاع مثلث ABC باشند، ثابت کنید. مثلث های ABC و MNP متشابه اند.
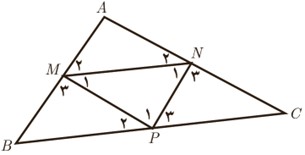
حل:
الف MN||BC و NP||AB و MP||AC چرا؟
ب بنابراین \({\widehat M_1} = {\widehat P_2} = \widehat C\) و \({\widehat N_1} = {\widehat P_3} = \widehat B\) (چرا؟)
از (ب) دربارهٔ مثلث های مورد نظر چه نتیجه ای می توان گرفت؟
الف
قبلا ثابت کردیم که هرگاه پاره خطی وسط دو ضلع مثلث را به هم وصل کند، با ضلع سوم موازی و نصف آن است.
ب
بنابر قضیه خطوط موازی داریم:
\(\left\{ \begin{array}{l}MN\parallel BC\,\not |\,NP \Rightarrow {{\hat N}_1} = {{\hat P}_3}\\\\MN\parallel BC\\\\MN\parallel NP\end{array} \right.\)
با این ویژگی ها، چهارضلعی MNPB متوازی الاضلاع می باشد؛ در نتیجه:
\(\begin{array}{l}{{\hat N}_1} = \hat B \Rightarrow {{\hat N}_1} = \hat B = {{\hat P}_3}\\\\\left\{ \begin{array}{l}MN\parallel BC\,\not |\,MP \Rightarrow {{\hat M}_1} = {{\hat P}_2}\\\\MN\parallel PC\\\\MN\parallel NC\end{array} \right.\end{array}\)
با این ویژگی ها، چهارضلعی MNCP نیز متوازی الاضلاع می باشد؛ در نتیجه:
\({\hat M_1} = \hat C \Rightarrow {\hat M_1} = \hat C = {\hat P_2}\)
ج
\(\left. {\begin{array}{*{20}{l}}{{{\hat N}_1} = \hat B}\\{}\\{{{\hat M}_1} = \hat C}\end{array}} \right\} \Rightarrow A\mathop B\limits^\Delta C\sim M\mathop N\limits^\Delta P\)
3 اگر سه مثلث ABC و \(A'B'C'\) و \(A''B''C''\) به گونه ای باشند که \(A\mathop B\limits^\Delta C \sim A'\mathop B\limits^\Delta 'C'\) و \(A'\mathop B\limits^\Delta 'C'\sim A''\mathop B\limits^\Delta ''C''\) دربارۀ دو مثلث ABC و \(A''B''C''\) چه می توان گفت؟ چرا؟
اگر \(A\mathop B\limits^\Delta C\sim A'\mathop B\limits^\Delta 'C'\) پس بنا به تعریف تشابه دو مثلث زوایای نظیر با هم برابرند:
\(\left\{ \begin{array}{l}\hat A = \hat A'\\\\\hat B = \hat B'\\\\\hat C = \hat C'\end{array} \right.\,\,\,\,\,\,\,\,\,\,(1)\)
اگر \(A'\mathop B\limits^\Delta 'C'\sim A''\mathop B\limits^\Delta ''C''\) پس بنا به تعریف تشابه دو مثلث زوایای نظیر با هم برابرند:
\(\left\{ \begin{array}{l}\hat A' = \hat A''\\\\\hat B' = \hat B''\\\\\hat C' = \hat C''\end{array} \right.\,\,\,\,\,\,\,\,\,\,(2)\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
