جواب تمرین صفحه 135 درس 6 ریاضی یازدهم تجربی (حد و پیوستگی)
تعداد بازدید : 84.77Mپاسخ تمرین صفحه 135 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 135 درس حد و پیوستگی
-تمرین صفحه 135 درس 6
-شما در حال مشاهده جواب تمرین صفحه 135 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با استفاده از قوانین حد و نمودارهای f و g حدهای زیر را (در صورت وجود) به دست آورید.
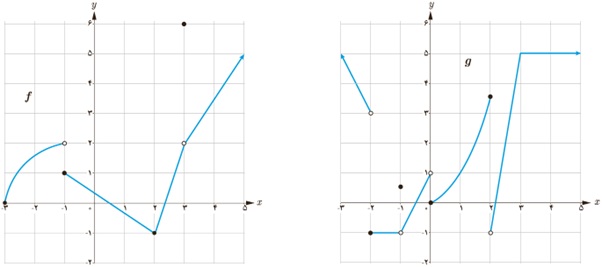
الف \(\mathop {\lim }\limits_{x \to 3} \;f\left( x \right)\)
ب \(\mathop {\lim }\limits_{x \to - 1} \;f\left( x \right)\)
پ \(\mathop {\lim }\limits_{x \to 3} \;g\left( x \right)\)
ت \(\mathop {\lim }\limits_{x \to 3} \;\left( {f\left( x \right) + g\left( x \right)} \right)\)
ث \(\mathop {\lim }\limits_{x \to - 1} \;\left( {f\left( x \right) + g\left( x \right)} \right)\)
ج \(\mathop {\lim }\limits_{x \to 2} \;\left( {2f\left( x \right) + 5g\left( x \right)} \right)\)
چ \(\mathop {\lim }\limits_{x \to 0} \;{\left( {f\left( x \right)} \right)^4}\)
ح \(\mathop {\lim }\limits_{x \to 0} \;{\left( {g\left( x \right)} \right)^2}\)
خ \(\mathop {\lim }\limits_{x \to 2} \;\frac{{f\left( x \right)}}{{g\left( x \right)}}\)
د \(\mathop {\lim }\limits_{x \to 5} \left( {f\left( x \right)\,.\,g\left( x \right)} \right)\)
الف \(\mathop {\lim }\limits_{x \to 3} \;f\left( x \right) = 2\)
ب \(\mathop {\lim }\limits_{x \to - 1} \;f\left( x \right) = \not \exists \) وجود ندارد
پ \(\mathop {\lim }\limits_{x \to 3} \;g\left( x \right) = {\rm{ }}5\)
ت \(\mathop {\lim }\limits_{x \to 3} \;\left( {f\left( x \right) + g\left( x \right)} \right) = {\rm{ }}\left( {2{\rm{ }} + {\rm{ }}5} \right){\rm{ }} = {\rm{ }}7\)
ث \(\mathop {\lim }\limits_{x \to - 1} \;\left( {f\left( x \right) + g\left( x \right)} \right) = \not \exists \) وجود ندارد
ج \(\mathop {\lim }\limits_{x \to 2} \;\left( {2f\left( x \right) + 5g\left( x \right)} \right) = \not \exists \) وجود ندارد
چ \(\mathop {\lim }\limits_{x \to 0} \;{\left( {f\left( x \right)} \right)^4} = {(\frac{1}{3})^4} = \frac{1}{{81}}\)
ح \(\mathop {\lim }\limits_{x \to 0} \;{\left( {g\left( x \right)} \right)^2} = \not \exists \) وجود ندارد
خ \(\mathop {\lim }\limits_{x \to 2} \;\frac{{f\left( x \right)}}{{g\left( x \right)}} = \not \exists \) وجود ندارد
د \(\mathop {\lim }\limits_{x \to 5} \left( {f\left( x \right)\,.\,g\left( x \right)} \right) = {\rm{ }}(5 \times 5){\rm{ }} = {\rm{ }}25\)
2 دو تابع متفاوت مثال بزنید که در یک نقطه دارای حدهای برابر باشند.
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}f\left( x \right) = \sqrt x \\\end{array}\\{g\left( x \right) = \left| x \right|}\end{array}} \right.\\\\\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \sqrt 1 = 1\\\\\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \left| 1 \right| = 1\end{array} \right.\\\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} g\left( x \right)\end{array}\)
3 حدهای زیر را در صورت وجود محاسبه کنید.
الف \(\mathop {\lim }\limits_{x \to 7} \;\left( { - 3} \right)\)
ب \(\mathop {\lim }\limits_{x \to 0} \;\left( { - 2x - 7} \right)\)
پ \(\mathop {\lim }\limits_{x \to - 1} \;\left( {3{x^2} - 4x + 5} \right)\)
ت \(\mathop {\lim }\limits_{x \to 3} \;\frac{{{x^2} - 3x}}{{{x^2} - 9}}\)
ث \(\mathop {\lim }\limits_{x \to 0} \;\frac{x}{{2{x^2} - x}}\)
ج \(\mathop {\lim }\limits_{x \to - 2} \;\frac{{{x^3} + 8}}{{x + 2}}\)
چ \(\mathop {\lim }\limits_{x \to - 2} \;\left[ x \right]\)
ح \(\mathop {\lim }\limits_{x \to {0^ + }} \;\sqrt x \)
خ \(\mathop {\lim }\limits_{x \to 2} \;\sqrt {x + 7} \)
د \(\mathop {\lim }\limits_{x \to {0^ - }} \;\sqrt x \)
ذ \(\mathop {\lim }\limits_{x \to 2} \;\sqrt {x + 5} \)
ر \(\mathop {\lim }\limits_{x \to 1} \;\sqrt {x - 2} \)
ز \(\mathop {\lim }\limits_{x \to {3^ + }} \;\frac{{x - 2}}{{\left[ x \right] + 1}}\)
ژ \(\mathop {\lim }\limits_{x \to - \frac{\pi }{3}} \;\cos x\)
س \(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \;\left( {\sin x + \cos x} \right)\)
ش \(\mathop {\lim }\limits_{x \to - {2^ + }} \;\frac{x}{{\left[ x \right]}}\)
ص \(\mathop {\lim }\limits_{x \to 2} \;\frac{{{x^2} + x - 6}}{{{x^2} - 6x + 8}}\)
ض \(\mathop {\lim }\limits_{x \to 0} \;\left( {x + \left[ x \right]} \right)\)
الف \(\mathop {\lim }\limits_{x \to 7} \;\left( { - 3} \right) = - 3\)
ب \(\mathop {\lim }\limits_{x \to 0} \;\left( { - 2x - 7} \right) = - 2\left( 0 \right) - 7 = - 7\)
پ \(\mathop {\lim }\limits_{x \to - 1} \;\left( {3{x^2} - 4x + 5} \right) = \)
\(3{\left( { - 1} \right)^2} - 4\left( { - 1} \right) + 5 = 12\)
ت \(\mathop {\lim }\limits_{x \to 3} \;\frac{{{x^2} - 3x}}{{{x^2} - 9}} = \mathop {\lim }\limits_{x \to 3} \,\,\frac{{x\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} = \)
\(\mathop {\lim }\limits_{x \to 3} \,\,\frac{x}{{\left( {x + 3} \right)}} = \frac{3}{{3 + 3}} = \frac{1}{2}\)
ث \(\mathop {\lim }\limits_{x \to 0} \;\frac{x}{{2{x^2} - x}} = \mathop {\lim }\limits_{x \to 0} \;\frac{x}{{x\left( {2x - 1} \right)}} = \)
\(\mathop {\lim }\limits_{x \to 0} \;\frac{1}{{2x - 1}} = \frac{1}{{2\left( 0 \right) - 1}} = - 1\)
ج \(\mathop {\lim }\limits_{x \to - 2} \;\frac{{{x^3} + 8}}{{x + 2}} = \)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 2} \;\frac{{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)}}{{\left( {x + 2} \right)}} = \\\\\mathop {\lim }\limits_{x \to - 2} \;\left( {{x^2} - 2x + 4} \right) = \\\\{\left( { - 2} \right)^2} - 2\left( { - 2} \right) + 4 = 12\end{array}\)
چ \(\mathop {\lim }\limits_{x \to - 2} \;\left[ x \right] = \not \exists \)وجود ندارد
ح \(\mathop {\lim }\limits_{x \to {0^ + }} \;\sqrt x = \sqrt {{0^ + }} = 0\)
خ \(\mathop {\lim }\limits_{x \to 2} \;\sqrt {x + 7} = \sqrt {2 + 7} = \sqrt 9 = 3\)
د \(\mathop {\lim }\limits_{x \to {0^ - }} \;\sqrt x = \sqrt {{0^ - }} = \not \exists \) وجود ندارد
ذ \(\mathop {\lim }\limits_{x \to 2} \;\sqrt {x + 5} = \sqrt {2 + 5} = \sqrt 7 \)
ر \(\mathop {\lim }\limits_{x \to 1} \;\sqrt {x - 2} = \sqrt {1 - 2} = \sqrt { - 1} = \not \exists \) وجود ندارد
ز \(\mathop {\lim }\limits_{x \to {3^ + }} \;\frac{{x - 2}}{{\left[ x \right] + 1}} = \frac{{{3^ + } - 2}}{{\left[ {{3^ + }} \right] + 1}} = \frac{{{1^ + }}}{{3 + 1}} = \frac{1}{4}\)
ژ \(\mathop {\lim }\limits_{x \to - \frac{\pi }{3}} \;\cos x = \cos ( - \frac{\pi }{3}) = \cos \frac{\pi }{3} = \frac{1}{2}\)
س \(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \;\left( {\sin x + \cos x} \right) = \)
\(\sin \frac{\pi }{4} + \cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2} = \sqrt 2 \)
ش \(\mathop {\lim }\limits_{x \to - {2^ + }} \;\frac{x}{{\left[ x \right]}} = \frac{{ - {2^ + }}}{{\left[ { - {2^ + }} \right]}} = \frac{{ - 2}}{{ - 2}} = 1\)
ص \(\mathop {\lim }\limits_{x \to 2} \;\frac{{{x^2} + x - 6}}{{{x^2} - 6x + 8}} = \)
\(\begin{array}{l} = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\left( {1 - \sin x} \right)\left( {1 + \sin x} \right)}}{{\left( {1 - \sin x} \right)}} = \\\\\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \left( {1 + \sin x} \right) = 1 + \sin \frac{\pi }{2} = \\\\1 + 1 = 2\end{array}\)
ض \(\mathop {\lim }\limits_{x \to 0} \;\left( {x + \left[ x \right]} \right) = \not \exists \) وجود ندارد
4 اگر \(\mathop {\lim }\limits_{x \to 2} \;f\left( x \right) = 3\) و \(\mathop {\lim }\limits_{x \to 2} \;g\left( x \right) = 0\) و \(\mathop {\lim }\limits_{x \to 2} \;h\left( x \right) = - 1\) حدهای زیر را در صورت وجود بیابید.
الف \(\mathop {\lim }\limits_{x \to 2} \;\left( {f\left( x \right) + h\left( x \right)} \right)\)
ب \(\mathop {\lim }\limits_{x \to 2} \;{\left( {h\left( x \right)} \right)^5}\)
پ \(\mathop {\lim }\limits_{x \to 2} \;\frac{{f\left( x \right)}}{{g\left( x \right)}}\)
ت \(\mathop {\lim }\limits_{x \to 2} \;\frac{{g\left( x \right)}}{{f\left( x \right)}}\)
ث \(\mathop {\lim }\limits_{x \to 2} \;\frac{{3f\left( x \right)}}{{g\left( x \right) - 5h\left( x \right)}}\)
ج \(\mathop {\lim }\limits_{x \to 2} \;\frac{1}{{h\left( x \right)}}\)
الف \(\mathop {\lim }\limits_{x \to 2} \;\left( {f\left( x \right) + h\left( x \right)} \right) = \)
\(\mathop {\lim }\limits_{x \to 2} f\left( x \right) + \mathop {\lim }\limits_{x \to 2} h\left( x \right) = 3 + \left( { - 1} \right) = 2\)
ب \(\mathop {\lim }\limits_{x \to 2} \;{\left( {h\left( x \right)} \right)^5} = {\left( { - 1} \right)^5} = - 1\)
پ \(\mathop {\lim }\limits_{x \to 2} \;\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 2} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 2} g\left( x \right)}} = \frac{3}{0} = \not \exists \) وجود ندارد
ت \(\mathop {\lim }\limits_{x \to 2} \;\frac{{g\left( x \right)}}{{f\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 2} g\left( x \right)}}{{\mathop {\lim }\limits_{x \to 2} f\left( x \right)}} = \frac{0}{3} = 0\)
ث \(\mathop {\lim }\limits_{x \to 2} \;\frac{{3f\left( x \right)}}{{g\left( x \right) - 5h\left( x \right)}} = \)
\(\frac{{3\mathop {\lim }\limits_{x \to 2} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 2} g\left( x \right) - 5\mathop {\lim }\limits_{x \to 2} h\left( x \right)}} = \frac{{3\left( 3 \right)}}{{\left( 0 \right) - 5\left( { - 1} \right)}} = \frac{9}{5}\)
ج \(\mathop {\lim }\limits_{x \to 2} \;\frac{1}{{h\left( x \right)}} = \frac{1}{{\mathop {\lim }\limits_{x \to 2} h\left( x \right)}} = \frac{1}{{ - 1}} = - 1\)
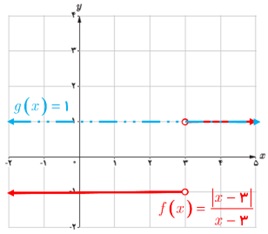
5 نمودار دو تابع \(f\left( x \right) = \frac{{\left| {x - 3} \right|}}{{x - 3}}\) و g(x) = 1 را رسم کنید. آیا \(\mathop {\lim }\limits_{x \to 3} \;f\left( x \right)\) موجود است؟ چرا؟ \(\mathop {\lim }\limits_{x \to 3} \;g\left( x \right)\) چطور؟ در چه نقاطی حد دو تابع با هم برابرند؟
\(\begin{array}{l}f\left( x \right) = \frac{{\left| {x - 3} \right|}}{{x - 3}} = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}1\;\;\:\:\:{\mkern 1mu} ,\;\;\:x > 3\\\end{array}\\{ - 1\;\;\:,\;\;\:x < 3}\end{array}} \right.\\\\g\left( x \right) = 1\\\\\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = 1\\\end{array}\\{\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = - 1}\end{array}} \right.\\\\ \Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right)\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = \not \exists \) وجود ندارد
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 3} \,g(x) = 1\\\\{x_0} > 3 \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} \,f(x) = \mathop {\lim }\limits_{x \to {x_0}} \,g(x)\\\\ \Rightarrow {x_0} \in (3\,,\,\infty )\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















