جواب تمرین صفحه 81 درس 4 حسابان دوازدهم (مشتق)
تعداد بازدید : 84.81Mپاسخ تمرین صفحه 81 حسابان دوازدهم
-گام به گام تمرین صفحه 81 درس مشتق
-تمرین صفحه 81 درس 4
-شما در حال مشاهده جواب تمرین صفحه 81 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 اگر \(f\left( x \right) = 3{x^2} - 2x + 1\) ، f’(2) را به دست آورید و معادله خط مماس بر منحنی f را در نقطه ای به طول 2 واقع بر آن بنویسید.
\(\begin{array}{l}f'(2) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) - f(2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{3{x^2} + 2x + 1 - 9}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{3{x^2} + 2x - 8}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)(3x + 4)}}{{x - 2}}\\\quad \quad \;{\kern 1pt} = \mathop {\lim }\limits_{x \to 2} (3x + 4) = 10\\ \Rightarrow y - 9 = 10(x - 2)\\ \Rightarrow y - 9 = 10x - 20\quad \Rightarrow \quad y = 10x - 11\end{array}\)
معادله خط مماس: \(y = 10x - 11\)
2 نقاط داده شده روی منحنی زیر را با شیب های ارائه شده در جدول نظیر کنید.
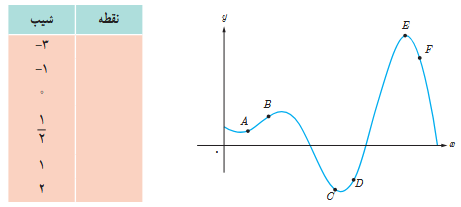
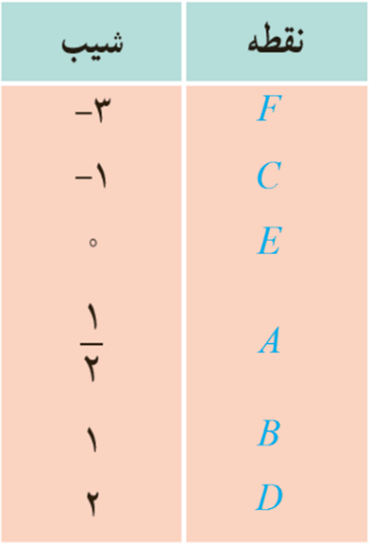
3 برای نمودار y=f(x) در شکل زیر شیب های داده شده از «الف» تا «ج» را از کوچک ترین به بزرگ ترین مرتب کنید.
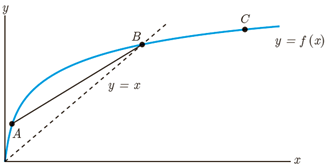
الف شیب نمودار در نقطه A
ب شیب نمودار در نقطه B
پ شیب نمودار در نقطه C
ت شیب خط AB
ث شیب خط y=2
ج شیب خط y=x
شیب های داده شده از «الف» تا «ج« را به ترتیب m2 ، m1 ، ... و m6 در نظر بگیرید.
الف
\({m_1}\)
ب
\({m_2}\)
پ
\({m_3}\)
ت
\({m_4}\)
ث
\({m_5} = 0\)
ج
\({m_6} = 1\)
\({m_5} < {m_2} < {m_3} < {m_4} < {m_6} < {m_1}\)
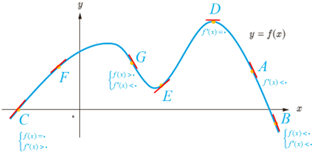
4 با در نظر گرفتن نمودار f در شکل، نقاط به طول های d، c، b، a و e را با مشتق های داده شده در جدول نظیر کنید.

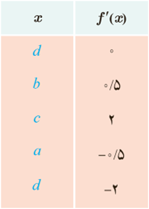
5 نقاطی مانند F، E، D، C، B، A و G را روی نمودار y=f(x) مشخص کنید به طوری که:
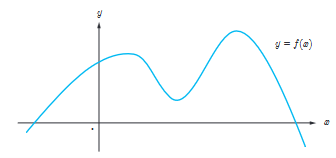
الف A ، نقطه ای روی نمودار است که شیب خط مماس بر نمودار در آن منفی است.
ب B نقطه ای روی نمودار تابع است که مقدار تابع و مقدار مشتق در آن منفی است.
پ C نقطه ای روی نمودار است که مقدار تابع در آنجا صفر است ولی مقدار مشتق در آن مثبت است.
ت D نقطه ای روی منحنی است که مشتق در آنجا صفر است.
ث نقاط E و F نقاط متفاوتی روی منحنی هستند که مشتق یکسان دارند.
ج G نقطه ای روی منحنی است که مقدار تابع در آنجا مثبت ولی مقدار مشتق منفی است.
6- اگر \(f'\left( { - 1} \right)\;,\;f\left( x \right) = {x^2} - 2\) را به دست آورید.
\(\begin{array}{l}f( - 1) = {( - 1)^3} - 2 = - 3\\ \Rightarrow f'( - 1) = \mathop {\lim }\limits_{x \to \; - 1} \frac{{f(x) - f( - 1)}}{{x + 1}} = \mathop {\lim }\limits_{x \to \; - 1} \frac{{{x^3} - 2 + 3}}{{x + 1}} = \mathop {\lim }\limits_{x \to \; - 1} \frac{{{x^3} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to \; - 1} \frac{{(x + 1)({x^2} - x + 1)}}{{x + 1}}\\\begin{array}{*{20}{c}}{}&{}&{}\end{array}\;\;\;{\kern 1pt} {\kern 1pt} = \mathop {\lim }\limits_{x \to \; - 1} ({x^2} - x + 1) = 3\end{array}\)
7 نقاط E، D، C، B، A و F را روی منحنی روبه رو در نظر می گیریم. در مورد شیب منحنی در این نقاط کدام گزاره درست و کدام یک نادرست است؟
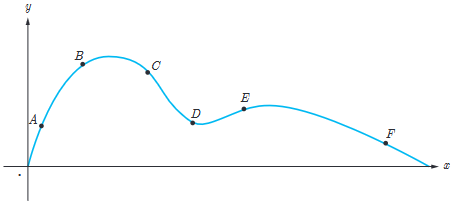
الف شیب منحنی در همه این نقاط مثبت است.
ب \({m_A} < {m_B}\) (شیب خط مماس بر منحنی در نقطه A را با mA نمایش داده ایم)
پ \({m_E} < {m_B} < {m_A}\)
ت شیب منحنی در نقاط F، D و C منفی است.
ث \({m_F} < {m_D} < {m_C}\)
ج \({m_C} < {m_D} < {m_F} < {m_E} < {m_B} < {m_A}\)
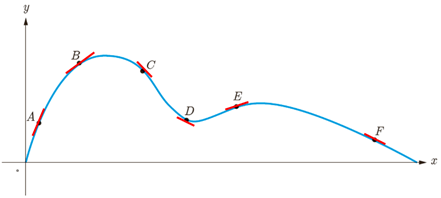
الف)
نادرست؛ مثلاً در نقطه شیب منفی است.
ب)
نادرست.
پ)
درست.
ت)
درست.
ث)
نادرست؛
ج)
نادرست.
الف
نادرست؛ مثلاً در نقطه F شیب منفی است.
ب
نادرست.
پ
درست.
ت
درست.
ث
نادرست؛ \({m_C} < {m_D} < {m_F}\)
ج
نادرست.
8 برای تابع f در شکل زیر داریم: f’(4)=1/5 و f(4)=25 با توجه به شکل مختصات نقاط B، A و C را بیابید.
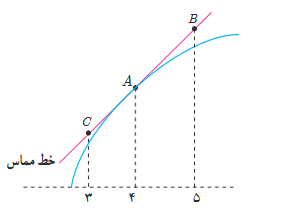
نقطه A که بر روی نمودار قرار دارد؛ پس مختصات آن معلوم است : \(A\left| {\begin{array}{*{20}{c}}4\\{25}\end{array}} \right.\)
حال نقاط B و C بر روی خطی قرار دارند که در نقطه A بر نمودار مماس هستند؛ پس بایستی ابتدا معادله خط مماس بر نمودار در نقطه A را بدست می آوریم و از آنجا مختصات باقی نقاط را محاسبه می کنیم:
\(\begin{array}{l}m = f'(4) = 1/5\\y - {y_A} = m(x - {x_A}) \Rightarrow y - 25 = 1/5(x - 4) \Rightarrow y = 1/5x + 19\\ \Rightarrow \left\{ \begin{array}{l}{x_B} = 5 \Rightarrow {y_B} = 26/5 \Rightarrow \quad B\left| {\begin{array}{*{20}{c}}5\\{26/5}\end{array}} \right.\\{x_C} = 3 \Rightarrow {y_C} = 23/5 \Rightarrow \quad C\left| {\begin{array}{*{20}{c}}3\\{23/5}\end{array}} \right.\end{array} \right.\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















