جواب تمرین صفحه 99 درس 4 حسابان دوازدهم (مشتق)
تعداد بازدید : 84.81Mپاسخ تمرین صفحه 99 حسابان دوازدهم
-گام به گام تمرین صفحه 99 درس مشتق
-تمرین صفحه 99 درس 4
-شما در حال مشاهده جواب تمرین صفحه 99 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 دو تابع مختلف مانند f و g مثال بزنید که هر دو در x=2 پیوسته باشند ولی در این نقطه مشتق پذیر نباشند.
\(f(x) = \left| {x - 2} \right|\quad ,\quad g(x) = \left\{ \begin{array}{l}{x^2}\quad \quad ,x < 2\\x + 2\quad ,x \ge 2\end{array} \right.\)
2 با محاسبه مشتق راست و مشتق چپ توابع داده شده در نقطه A، نشان دهید که این توابع در نقطه A مشتق پذیر نیستند.

الف
\(\left\{ \begin{array}{l}{f_ + }^\prime (0) = 2(0) = 0\\{f_ - }^\prime (0) = - 1\end{array} \right.\)
وجود ندارد \({f^\prime }(0)\;:\)
ب
\(\left\{ \begin{array}{l}{f_ + }^\prime (1) = \frac{{ - 1}}{{{{(1)}^2}}} = - 1\\{f_ - }^\prime (1) = 0\end{array} \right.\)
وجود ندارد \({f^\prime }(1)\;:\)
پ
\(\left\{ \begin{array}{l}{f_ + }^\prime (4) = \frac{1}{2}\\{f_ - }^\prime (4) = \frac{1}{{2\sqrt 4 }} = \frac{1}{4}\end{array} \right.\)
وجود ندارد \({f^\prime }(2)\;:\)
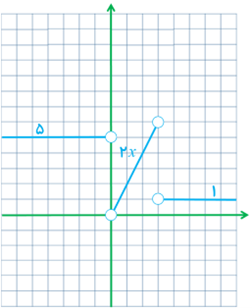
3 تابع \(f\left( x \right) = \left\{ \begin{array}{l}5x - 4\;\;\;\;\;\;\;\;x < 0\\{x^2}\;\;\;\;\;\;\;\;\;\;0 \le x \le 3\\x + 6\;\;\;\;\;\;\;\;\;\;x > 3\end{array} \right.\) داده شده است.
الف نمودار تابع f را رسم کنید.
ب با توجه به نمودار تابع f بگویید که چرا f’(0) و f’(3) وجود ندارند؟
پ ضابطه تابع مشتق را بنویسید.
ت نمودار تابع \(f’\) را رسم کنید.
الف

ب
\({f^\prime }(0)\) وجود ندارد چون تابع در \(x = 0\) ناپیوسته است.
\({f^\prime }(3)\) وجود ندارد \({f_ + }^\prime (3) = 1\quad ,{f_ - }^\prime (3) = 6\quad \to \)
پ
\(f'(x) = \left\{ \begin{array}{l}5\quad \quad x < 0\\2x\quad \;\,{\kern 1pt} 0 < x < 3\\1\quad \quad x > 3\end{array} \right.\)
ت
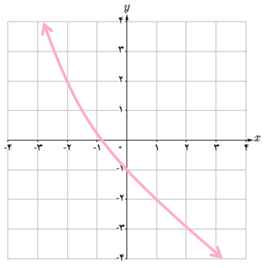
4 نمودار تابعی را رسم کنید که مشتق آن
الف در یک نقطه برابر صفر شود.
ب در x=2 برابر 3 شود
پ در تمام نقاط مثبت باشد.
ت در تمام نقاط یکسان باشد.
ث در تمام نقاط منفی باشد.
الف
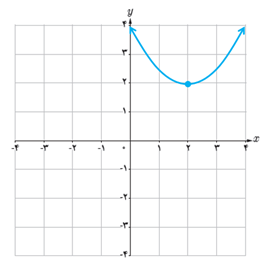
ب
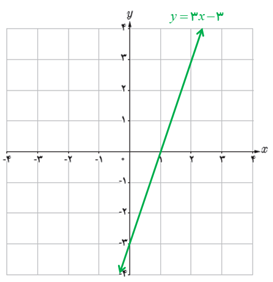
پ

ت
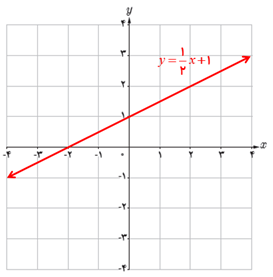
ث
5
الف با استفاده از نمودار تابع \(f\left( x \right) = {x^2} + 2x + 3\) (شکل مقابل) مقادیر زیر را به ترتیب صعودی مرتب کنید.
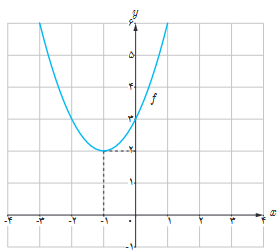
f'(3) و f’(0) و f’(-1) و f’(2)
ب صحت ادعای خود در (الف) را با محاسبه مشتق تابع\(f\left( x \right) = {x^2} + 2x + 3\) بررسی کنید.
پ تابع مشتق را رسم کنید.
الف
\(0 = f'( - 1) < f'(0) < f'(2) < f'(3)\)
ب
\(f'(x) = 2x + 2 \Rightarrow \left\{ \begin{array}{l}f'( - 1) = 0\\f'(0) = 2\\f'(2) = 6\\f'(3) = 8\end{array} \right.\)
پ
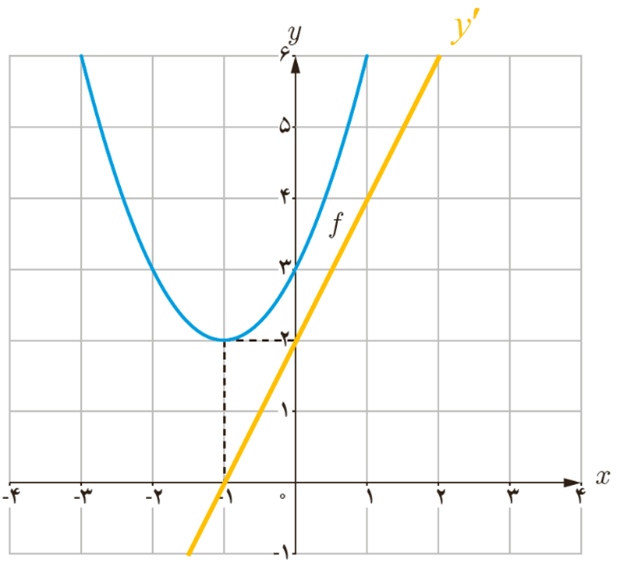
6 مشتق پذیری تابع\(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + 3\;\;\;\;\;x \ge 1\\2x\;\;\;\;\;\;\;\;\;x < 1\end{array} \right.\) را در نقطه x=1 بررسی کنید.
تابع در نقطه \(x = 1\) ناپیوسته است؛ پس در این نقطه مشتق پذیر نیست \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f(x) = 1\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = 2\end{array} \right. \to \)
7 سه تابع مختلف مثال بزنید که مشتق آنها با هم برابر باشند.
\(\left\{ \begin{array}{l}f(x) = 3x\\g(x) = 3x - 10\\h(x) = 3x + 5\end{array} \right.\)
8 اگر \(f(x) = |x2-4|\) به کمک تعریف مشتق، مشتق پذیری f را در نقاط به طول های 2 و 2- بررسی کنید.
\(\left\{ \begin{array}{l}f(x) = \left\{ \begin{array}{l}{x^2} - 4\quad \quad \quad ,x < - 2\\ - ({x^2} - 4)\quad \;\,{\kern 1pt} {\kern 1pt} {\kern 1pt} , - 2 \le x \le 2\\{x^2} - 4\quad \quad \quad ,x > 2\end{array} \right.\\f'(x) = \left\{ \begin{array}{l}2x\quad \quad \quad ,x < - 2\\ - 2x\quad \;\,{\kern 1pt} \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} , - 2 < x < 2\\2x\quad \quad \quad ,x > 2\end{array} \right.\end{array} \right.\quad \Rightarrow \quad \left\{ \begin{array}{l}\left\{ \begin{array}{l}{f_ + }^\prime (2) = 4\\{f_ - }^\prime (2) = - 4\end{array} \right. \Rightarrow {f_ + }^\prime (2) \ne {f_ - }^\prime (2) \Rightarrow \cancel{\exists }f'(2)\\\left\{ \begin{array}{l}{f_ + }^\prime ( - 2) = 4\\{f_ - }^\prime ( - 2) = - 4\end{array} \right. \Rightarrow {f_ + }^\prime ( - 2) \ne {f_ - }^\prime ( - 2) \Rightarrow \cancel{\exists }f'( - 2)\end{array} \right.\)
9 مشتق تابع \(f\left( x \right) = \sqrt[3]{{{x^2}}}\) را به دست آورده و مشخص کنید در چه نقطه ای مماس قائم دارد؟
\(\begin{array}{l}f(x) = \sqrt[3]{{{x^2}}} = {x^{\frac{2}{3}}} \Rightarrow f'(x) = \frac{2}{3}{x^{\frac{2}{3} - 1}} = \frac{2}{3}{x^{\frac{{ - 1}}{3}}} = \frac{2}{{3\sqrt[3]{x}}}\\ \Rightarrow \left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to \;{0^ - }} f'(x) = \mathop {\lim }\limits_{x \to \;{0^ - }} \frac{2}{{3\sqrt[3]{x}}} = \frac{2}{{{0^ - }}} = - \infty \\\mathop {\lim }\limits_{x \to \;{0^ + }} f'(x) = \mathop {\lim }\limits_{x \to \;{0^ + }} \frac{2}{{3\sqrt[3]{x}}} = \frac{2}{{{0^ + }}} = + \infty \end{array} \right. \Rightarrow x = 0\end{array}\)
تابع در نقطه\(x = 0\) پیوسته است و ومماس قائم دارد.
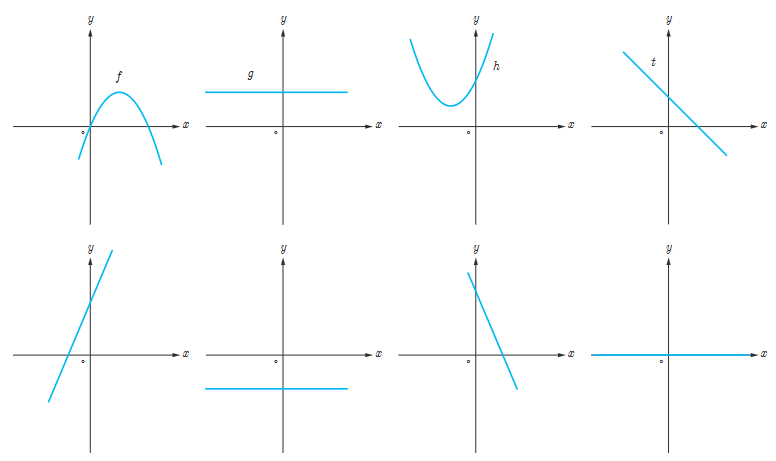
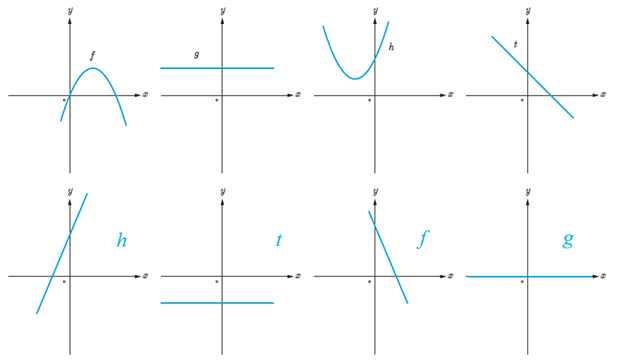
10 نمودار توابع f و g و h و t را به نمودار مشتق آنها، نظیر کنید.
11 نمودار توابع f و g را در شکل مقابل درنظر بگیرید.
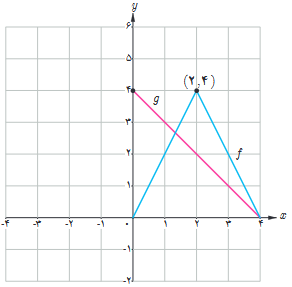
الف اگر h(x)=f(x).g(x) مطلوب است h’(2) ، h’(1) و h’(3)
ب اگر \(k\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) مطلوب است k’(2) ، k’(1) و k’(3)
الف
\(\begin{array}{l}\left\{ \begin{array}{l}f(1) = 2\\f'(1) = 2\\g(1) = 3\\g'(1) = - 1\end{array} \right. \Rightarrow h'(1) = f'(1) \cdot g(1) + f(1) \cdot g'(1) = 2 \times 3 + 2 \times ( - 1) = 4\\\left\{ \begin{array}{l}f(2) = 4\\f'(2) = \xcancel{{}}\\g(2) = 2\\g'(2) = - 1\end{array} \right. \Rightarrow h'(2) = f'(2) \cdot g(2) + f(2) \cdot g'(2) = \xcancel{{}} \Rightarrow \xcancel{\exists }h'(2)\\\left\{ \begin{array}{l}f(3) = 2\\f'(3) = - 2\\g(3) = 1\\g'(3) = - 1\end{array} \right. \Rightarrow h'(3) = f'(3) \cdot g(3) + f(3) \cdot g'(3) = ( - 2) \times 1 + 2 \times ( - 1) = - 4\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}f(1) = 2\\f'(1) = 2\\g(1) = 3\\g'(1) = - 1\end{array} \right. \Rightarrow k'(1) = \frac{{f'(1) \cdot g(1) - f(1) \cdot g'(1)}}{{{g^2}(1)}} = \frac{{2 \times 3 - 2 \times ( - 1)}}{{{3^2}}} = \frac{8}{9}\\\left\{ \begin{array}{l}f(2) = 4\\f'(2) = \xcancel{{}}\\g(2) = 2\\g'(2) = - 1\end{array} \right. \Rightarrow k'(2) = \frac{{f'(2) \cdot g(2) - f(2) \cdot g'(2)}}{{{g^2}(2)}} = \xcancel{{}} \Rightarrow \xcancel{\exists }k'(2)\\\left\{ \begin{array}{l}f(3) = 2\\f'(3) = - 2\\g(3) = 1\\g'(3) = - 1\end{array} \right. \Rightarrow k'(3) = \frac{{f'(3) \cdot g(3) - f(3) \cdot g'(3)}}{{{g^2}(3)}} = \frac{{( - 2) \times 1 - 2 \times ( - 1)}}{{{1^2}}} = 0\end{array}\)
12 اگر f’(1)=3 و g’(1)=5 مطلوب است، \((f+g)’(1)\) و \((3f+2g)’(1)\)
\(\begin{array}{l}(f + g)'(1) = f'(1) + g'(1) = 3 + 5 = 8\\\\(3f + 2g)'(1) = 3f'(1) + 2g'(1) = 3 \times 3 + 2 \times 5 = 19\end{array}\)
13 اگر \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}\;\;\;\;x \le 0\\x\;\;\;\;\;x > 0\end{array} \right.\) نشان دهید \(f{'_ + }(0)\) و \(f{'_ - }(0)\) موجودند ولی f’(0) موجود نیست.
\(f(x) = \left\{ \begin{array}{l}{x^2}\quad \quad x \le 0\\x\quad \quad \,\;x > 0\end{array} \right. \Rightarrow f'(x) = \left\{ \begin{array}{l}2x\quad \quad x < 0\\1\quad \quad \,\;\;x > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{f_ - }^\prime (0) = 2 \times 0 = 0\\{f_ + }^\prime (0) = 1\end{array} \right. \Rightarrow {f_ - }^\prime (0) \ne {f_ + }^\prime (0) \Rightarrow \cancel{\exists }{f^\prime }(0)\)
14 مشتق توابع داده شده را به دست آورید.
\(f\left( x \right) = \left( {3{x^2} - 4} \right){\left( {2x - 5} \right)^2}\) الف
\(f\left( x \right) = \left( {\sqrt {3x + 2} } \right)\left( {{x^3} + 1} \right)\) ب
\(f\left( x \right) = \frac{{{x^2} - 3x + 1}}{{ - 3x + 2}}\) پ
\(f\left( x \right) = \frac{{9x - 2}}{{\sqrt x }}\) ت
الف
\(f\left( x \right) = \left( {3{x^2} - 4} \right){\left( {2x - 5} \right)^2} \Rightarrow f'(x) = 6x{(2x - 5)^3} + 3(2){(2x - 5)^2}(3{x^2} - 4)\)
ب
\(f\left( x \right) = \left( {\sqrt {3x + 2} } \right)\left( {{x^3} + 1} \right) \Rightarrow f'(x) = \frac{{(2x - 3)( - 3x + 2) - ({x^2} - 3x + 1)( - 3)}}{{{{( - 3x + 2)}^2}}}\)
پ
\(f\left( x \right) = \frac{{{x^2} - 3x + 1}}{{ - 3x + 2}} \Rightarrow f'(x) = \frac{3}{{2\sqrt {3x + 2} }}({x^3} + 1) + 3{x^2}\sqrt {3x + 2} \)
ت
\(f\left( x \right) = \frac{{9x - 2}}{{\sqrt x }} \Rightarrow f'(x) = \frac{{9\sqrt x - \left( {9x - 2} \right)\frac{1}{{2\sqrt x }}}}{x}\)
15 مشتق توابع مثلثاتی زیر را به دست آورید.
\(f\left( x \right) = {\sin ^3}x + {\cos ^2}x\) الف
\(f\left( x \right) = {\tan ^2}x - 2\cos x\) ب
\(f\left( x \right) = \frac{{1 - \sin x}}{{1 + \sin x}}\) پ
\(f\left( x \right) = \sin x\;\cos 2x\) ت
الف
\(f\left( x \right) = {\sin ^3}x + {\cos ^2}x \Rightarrow f'(x) = 3\cos x{\sin ^2}x - 2\sin x\cos x\)
ب
\(f\left( x \right) = {\tan ^2}x - 2\cos x \Rightarrow f'(x) = \frac{{ - \cos x(1 + \sin x) - (1 - \sin x)cosx}}{{{{(1 + \sin x)}^2}}} = \frac{{ - 2\cos x}}{{{{(1 + \sin x)}^2}}}\)
پ
\(f\left( x \right) = \frac{{1 - \sin x}}{{1 + \sin x}} \Rightarrow f'(x) = 2(1 + {\tan ^2}x)\tan x + 2\sin x\)
ت
\(f\left( x \right) = \sin x\;\cos 2x \Rightarrow f'(x) = \cos x\cos 2x - 2\sin x\sin 2x\)
16 اگر \(f\left( x \right) = {\sin ^2}x - \cos 2x\) مقادیر زیر را حساب کنید.
\(f''\left( {\frac{\pi }{6}} \right)\) الف
\(f''\left( {\frac{\pi }{2}} \right) - f'\left( {\frac{\pi }{2}} \right)\) ب
\(\begin{array}{l}f'(x) = 2\cos x\sin x + 2\sin 2x = \sin 2x + 2\sin 2x = 3\sin 2x\\\\f''(x) = 6\cos 2x\end{array}\)
الف
\(f''\left( {\frac{\pi }{6}} \right) = 6\cos (2 \times \frac{\pi }{6}) = 6\cos (\frac{\pi }{3}) = 6 \times \frac{1}{2} = 3\)
ب
\(f''\left( {\frac{\pi }{2}} \right) - f'\left( {\frac{\pi }{2}} \right) = 6\cos (2 \times \frac{\pi }{2}) - 3sin(2 \times \frac{\pi }{2}) = 6\cos (\pi ) - 3sin(\pi ) = - 6\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















