جواب تمرین صفحه 151 درس 7 ریاضی یازدهم تجربی (آمار و احتمال)
تعداد بازدید : 84.76Mپاسخ تمرین صفحه 151 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 151 درس آمار و احتمال
-تمرین صفحه 151 درس 7
-شما در حال مشاهده جواب تمرین صفحه 151 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در پرتاب یک تاس فرض کنید پیشامد A ظاهر شدن عدد زوج، پیشامد B ظاهر شدن عددی مضرب 3 و پیشامد C ظاهر شدن عددی بزرگ تر از 2 باشد. مستقل یا غیرمستقل بودن هر دو پیشامد را بررسی کنید.
ابتدا احتمال رخ دادن هر پیشامد را محاسبه می کنیم:
\(\begin{array}{l}A = \left\{ {2\:,\:4\:,\:6} \right\} \Rightarrow P\left( A \right) = \frac{3}{6} = \frac{1}{2}\\\\B = \left\{ {3\:,\:6} \right\} \Rightarrow P\left( B \right) = \frac{2}{6} = \frac{1}{3}\\\\C = \left\{ {3\:,\:4\:,\:5\:,\:6} \right\} \Rightarrow P\left( C \right) = \frac{4}{6} = \frac{2}{3}\end{array}\)
احتمال ظاهر شدن عدد زوج به شرط ظاهر شدن مضرب 3:
\(\begin{array}{l}A \cap B = \left\{ 6 \right\} \Rightarrow P\left( {A \cap B} \right) = \frac{1}{6}\\\\ \Rightarrow P\left( {\left. A \right|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{{\frac{1}{6}}}{{\frac{1}{3}}} = \frac{1}{2}\\\\ \Rightarrow P\left( {\left. A \right|B} \right) = P\left( A \right)\end{array}\)
پیشامد A مستقل از پیشامد B می باشد.
احتمال ظاهر شدن عدد زوج به شرط ظاهر شدن عددی بزرگ تر از 2:
\(\begin{array}{l}A \cap C = \left\{ {4\:,\:6} \right\} \Rightarrow P\left( {A \cap C} \right) = \frac{1}{3}\\\\ \Rightarrow P\left( {\left. A \right|C} \right) = \frac{{P\left( {A \cap C} \right)}}{{P\left( C \right)}} = \frac{{\frac{1}{3}}}{{\frac{2}{3}}} = \frac{1}{2}\\\\ \Rightarrow P\left( {\left. A \right|C} \right) = P\left( A \right)\end{array}\)
پیشامد A مستقل از پیشامد C می باشد
2 یک سکه را سه بار پرتاب می کنیم. احتمال رو آمدن سکه در پرتاب سوم را به دست آورید، به شرط اینکه در دو پرتاب اول و دوم، پشت ظاهر شده باشد.
پشت : p
ظاهر شدن رو : r
\(\begin{array}{l}S{\rm{ }} = \left\{ {\left( {r,r,r} \right),\left( {r,r,p} \right),\left( {r,p,r} \right),} \right.\\\\\left( {r,p,p} \right),\left( {p,r,r} \right),\left( {p,r,p} \right),\\\\\left. {\left( {p,p,r} \right),\left( {p,p,p} \right)} \right\}\end{array}\)
احتمال رو شدن سکه در پرتاب سوم:
\(\begin{array}{l}A = \left\{ {\left( {r\:,\:r\:,\:r} \right)\:,\:\left( {r\:,\:p\:,\:r} \right)\:,\:} \right.\\\\\left. {\left( {p\:,\:r\:,\:r} \right)\:,\:\left( {p\:,\:p\:,\:r} \right)} \right\}\\\\ \Rightarrow P\left( A \right) = \frac{4}{8} = \frac{1}{2}\end{array}\)
احتمال پشت شدن سکه در پرتاب اول و دوم:
\(\begin{array}{l}B = \left\{ {\left( {p\:,\:p\:,\:r} \right)\:,\:\left( {p\:,\:p\:,\:p} \right)} \right\}\\\\ \Rightarrow P\left( B \right) = \frac{2}{8} = \frac{1}{4}\\\\ \Rightarrow P\left( {\left. A \right|B} \right) = \frac{1}{2}\end{array}\)
احتمال رو شدن سکه در پرتاب سوم به شرط پشت شدن سکه در پرتاب اول و دوم:
\(P\left( {\left. A \right|B} \right) = \frac{1}{2}\)
3 فرض کنید A و B دو پیشامد ناتهی و مستقل از یکدیگرند.
الف نشان دهید A' و B مستقل اند.
ب با توجه به (الف) نشان دهید A' و B' نیز مستقل اند.
الف چون پیشامدهای A و B مستقل اند، داریم:
\(P\left( {A \cap B} \right) = P\left( A \right) \times P\left( B \right)\)
می خواهیم ثابت کنیم :
\(P\left( {A' \cap B} \right) = P\left( {A'} \right) \times P\left( B \right)\)
داریم:
\(\begin{array}{l}P\left( {A'} \right) \times P\left( B \right) = \\\\\left( {1 - P\left( A \right)} \right) \times P\left( B \right) = \\\\P\left( B \right) - P\left( A \right) \times P\left( B \right) = \\\\P\left( B \right) - P\left( {A \cap B} \right) = \\\\P\left( {B - A} \right) = \\\\P\left( {B \cap A'} \right) = P\left( {A' \cap B} \right)\end{array}\)
ب می خواهیم ثابت کنیم :
\(P\left( {A' \cap B'} \right) = P\left( {A'} \right) \times P\left( {B'} \right)\)
داریم:
\(\begin{array}{l}P\left( {A'} \right) \times P\left( {B'} \right) = \\\\\left( {1 - P\left( A \right)} \right) \times \left( {1 - P\left( B \right)} \right) = \\\\1 - P\left( A \right) - P\left( B \right) + P\left( A \right) \times P\left( B \right) = \\\\1 - \left( {P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)} \right) = \\\\1 - P\left( {A \cup B} \right) = \\\\P\left( {{{\left( {A \cup B} \right)}^\prime }} \right) = P\left( {A' \cap B'} \right)\end{array}\)
4 احمد به احتمال 0/7 در تیم کوهنوردی مدرسه شان و به احتمال 0/8 در تیم ملی فوتبال نوجوانان انتخاب می شود. احتمال های زیر را محاسبه کنید.
الف در هر دو تیم مورد نظر انتخاب شود.
ب در هیچ کدام از دو تیم انتخاب نشود.
پ فقط در تیم ملی فوتبال انتخاب شود.
ت فقط در یکی از تیم ها انتخاب شود.
ث حداقل در یکی از تیم ها انتخاب شود.
A : انتخاب در تیم کوهنوردی
B : انتخاب در تیم ملی فوتبال نوجوانان
الف باید  را بدست آوریم و چون پیشامدهای A و B مستقل از یکدیگرند، داریم:
را بدست آوریم و چون پیشامدهای A و B مستقل از یکدیگرند، داریم:
\(\begin{array}{l}P\left( {A \cap B} \right) = P\left( A \right) \times P\left( B \right) = \\\\0/7 \times 0/8 = 0/56\end{array}\)
ب باید  را بدست آوریم و چون پیشامدهای A’ و B’ مستقل از یکدیگرند، داریم:
را بدست آوریم و چون پیشامدهای A’ و B’ مستقل از یکدیگرند، داریم:
\(\begin{array}{l}P\left( {A'} \right) = 1 - P\left( A \right) = 1 - 0/7 = 0/3\\\\P\left( {B'} \right) = 1 - P\left( B \right) = 1 - 0/8 = 0/2\\\\P\left( {A' \cap B'} \right) = P\left( {A'} \right) \times P\left( {B'} \right) = \\\\0/3 \times 0/2 = 0/06\end{array}\)
پ باید 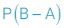 را بدست آوریم، پس داریم:
را بدست آوریم، پس داریم:
\(\begin{array}{l}P\left( {B - A} \right) = P\left( {B \cap A'} \right) = \\\\P\left( B \right) \times P\left( {A'} \right) = 0/8 \times 0/3 = \\\\0/24\end{array}\)
ت باید 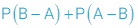 را بدست آوریم، پس داریم:
را بدست آوریم، پس داریم:
\(\begin{array}{l}P\left( {A - B} \right) = P\left( {A \cap B'} \right) = \\\\P\left( A \right) \times P\left( {B'} \right) = 0/7 \times 0/2 = \\\\0/14\\\\ \Rightarrow P\left( {B - A} \right) + P\left( {A - B} \right) = 0/38\end{array}\)
ث باید  را بدست آوریم، پس داریم:
را بدست آوریم، پس داریم:
\(\begin{array}{l}P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right) = \\\\0/7 + 0/8 - 0/56 = 0/94\end{array}\)
5 احتمال اینکه رؤیا در درس ریاضی قبول شود، دو برابر احتمال آن است که دوستش در این درس قبول شود. اگر احتمال اینکه حداقل یکی از آنها در درس ریاضی قبول شوند، برابر 0/625 باشد، رؤیا با چه احتمالی در این درس قبول خواهد شد؟
A : پیشامد قبول شدن رؤیا در درس ریاضی
B : پیشامد قبول شدن دوستش در درس ریاضی
\(\begin{array}{l}P\left( {A \cup B} \right) = 0/625\\\\P\left( A \right) = 2\,P\left( B \right)\\\\P\left( A \right) = ?\end{array}\)
چون دو پیشامد از هم مستقل هستند، داریم:
\(\begin{array}{l}P\left( {A \cap B} \right) = P\left( A \right) \times P\left( B \right)\\\\P\left( A \right) = 2\,P\left( B \right)\\\\ \Rightarrow P\left( B \right) = \frac{1}{2}P\left( A \right)\\\\ \Rightarrow P\left( {A \cap B} \right) = \frac{1}{2}{\left( {P\left( A \right)} \right)^2}\\\\P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\\\\P\left( A \right) = x \Rightarrow 0 \le x \le 1\,\,\,(I)\\\\ \Rightarrow 0/625 = x + \frac{1}{2}x - \frac{1}{2}{x^2}\\\\ \Rightarrow {x^2} - 3x + 1/25 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = 2/5}\\{{x_2} = 0/5}\end{array}} \right.\,\,\,(II)\\\\(I)\,,\,(II) \Rightarrow x = 0/5\\\\ \Rightarrow P\left( A \right) = 0/5\end{array}\)
6 دو تاس با هم پرتاب شده اند. احتمال آنکه هر دو عدد رو شده زوج باشند، به شرط اینکه بدانیم مجموع اعداد رو شده برابر 8 است را به دست آورید.
A : هر دو عدد رو شده زوج باشد
B : مجموع هر دو عدد رو شده 8 باشد
\(\begin{array}{l}B = \left\{ {\left( {2\:,\:6} \right)\:,\:\left( {6\:,\:2} \right)\:,\:\left( {5\:,\:3} \right)\:,} \right.\\\\\left. {\left( {3\:,\:5} \right)\:,\:\left( {4\:,\:4} \right)} \right\}\\\\ \Rightarrow n\left( B \right) = 5\\\\A \cap B = \left\{ {\left( {2\:,\:6} \right)\:,\:\left( {6\:,\:2} \right)\:,\:\left( {4\:,\:4} \right)} \right\}\\\\ \Rightarrow n\left( {A \cap B} \right) = 3\\\\ \Rightarrow P\left( {\left. A \right|B} \right) = \frac{{n\left( {A \cap B} \right)}}{{n\left( B \right)}} = \frac{3}{5}\end{array}\)
7 ترکیبی از 4 ماده شیمیایی داریم که دو تا از آنها مواد A و B هستند. احتمال واکنش نشان دادن ماده A ، 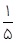 و احتمال واکنش نشان دادن ماده B ،
و احتمال واکنش نشان دادن ماده B ، 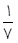 است. اگر ماده A واکنش نشان دهد، احتمال واکنش نشان دادن ماده B ،
است. اگر ماده A واکنش نشان دهد، احتمال واکنش نشان دادن ماده B ، 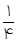 خواهد شد. با چه احتمالی حداقل یکی از مواد A یا B واکنش نشان خواهد داد؟
خواهد شد. با چه احتمالی حداقل یکی از مواد A یا B واکنش نشان خواهد داد؟
\(\begin{array}{l}\left. \begin{array}{l}P\left( A \right) = \frac{1}{5}\\\\P\left( B \right) = \frac{1}{7}\\\\P\left( {\left. B \right|A} \right) = \frac{1}{4}\end{array} \right\} \Rightarrow P\left( {A \cup B} \right) = ?\\\\P\left( {\left. B \right|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}}\\\\ \Rightarrow \frac{1}{4} = \frac{{P\left( {A \cap B} \right)}}{{\frac{1}{5}}}\\\\ \Rightarrow P\left( {A \cap B} \right) = \frac{1}{{20}}\\\\P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right) = \\\\\frac{1}{5} + \frac{1}{7} - \frac{1}{{20}} = \frac{{41}}{{140}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















