جواب مرور راهبرد ها صفحه 10 درس 1 ریاضی هفتم (راهبردهای حل مسئله)
تعداد بازدید : 86.39Mپاسخ مرور راهبرد ها صفحه 10 ریاضی هفتم
-گام به گام مرور راهبرد ها صفحه 10 درس راهبردهای حل مسئله
-مرور راهبرد ها صفحه 10 درس 1
-شما در حال مشاهده جواب مرور راهبرد ها صفحه 10 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1- \(\frac{1}{3}\) دانش آموزان کلاسی بسکتبال و \(\frac{1}{5}\) دانش آموزان آن کلاس، فوتبال بازی می کنند. سایر دانش آموزان که تعدادشان 14 نفر است، بازی آنها را تماشا می کنند. این کلاس چند دانش آموز دارد؟
ابتدا کسری از کلاس را که در حال ورزش کردن هستند را بدست می آوریم؛ سپس آن را از مقدار 1 کم کرده تا آن کسر از بچه هایی که در حال تماشا کردن بازی ها را هستند بدست می آوریم. از آن جا تعداد دانش آموزان کلاس را بدست می آوریم؛ بنابراین:
\(\frac{1}{3} + \frac{1}{5} = \frac{{5 + 3}}{{15}} = \frac{8}{{15}}\)
\(\frac{8}{{15}}\) بچه ها در حال ورزش کردن هستند.
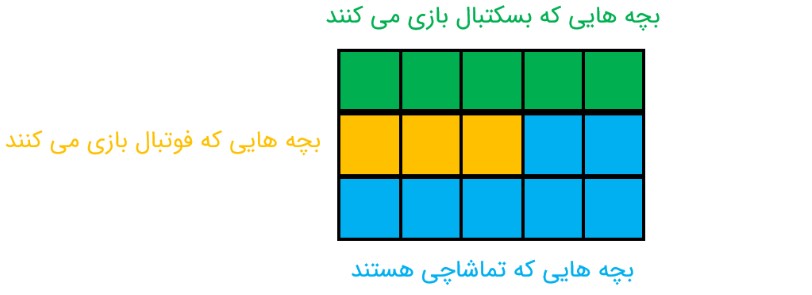
با توجه به رنگ ها مشخص می شود که \(\frac{7}{{15}}\) از بچه ها مشغول تماشای بازی هستند که تعداد آن ها برابر با 14 نفر است؛ پس از آن جهت که هفت خانه مربوط به تماشاچی ها برابر با 14 نفر است، پس مشخص می شود که هر خانه نماینده 2 نفر است؛ بنابراین تعداد دانش آموزان این کلاس 30 نفر می باشند:
30 = 15 × 2
2- مساحت مربعی به ضلع 100 سانتی متر، 1متر مربع است. اگر از ضلع مربع 10 درصد کم کنیم، مساحت مربع چند درصد کم می شود؟
از راهبرد زیر مسئله استفاده می کنیم:
الف) ابتدا 10 درصد 100 سانتی متر را محاسبه می کنیم که برابر 10 سانتی متر می شود:
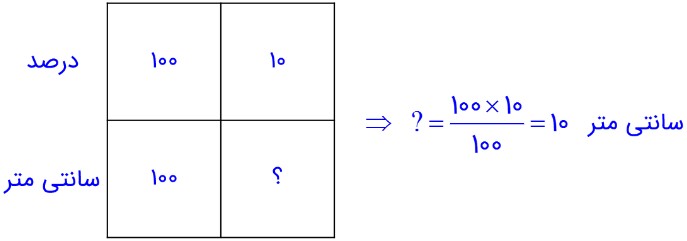
ب) طول ضلع مربع جدید را حساب می کنیم:
سانتی متر 90 = 10 – 100
پ) مساحت هر دو مربع قدیم و جدید را بر اساس سانتی متر محاسبه می کنیم:
سانتی متر مربع 10000 = 100 × 100 مربع قدیم
سانتی متر مربع 8100 = 90 × 90 مربع قدیم
ت) نسبت مساحت مربع جدید به مساحت مربع قدیم را حساب می کنیم:
\(\frac{{8100}}{{10000}} = \frac{{81}}{{100}} = \% 81\)
ث) اختلاف مساحت ها را به صورت درصد می نویسیم:
%100 - %81 = %19
بنابراین مساحت مربع جدید 19% از مربع قدیم کمتر است.
3- کشاورزی زمین خود را به نسبت های زیر بذر پاشی کرده است:
گندم: %45 جو: %37/5 ذرت: % 17/5
اگر مساحت زمین او 15 هکتار باشد، مساحت زیر کشت هر بذر را حساب کنید.
از راهبرد زیر مسئله کمک می گیریم:
الف) مساحت زیر کشت گندم را محاسبه می کنیم:
\(\frac{{45}}{{100}} = \frac{?}{{15}} \Rightarrow ? = \frac{{45 \times 15}}{{100}} = \frac{{675}}{{100}} = 6/75\)
این کشاورز 6/75 هکتار از زمین خود را گندم کاشته است.
ب) مساحت زیر کشت جو را محاسبه می کنیم:
\(\frac{{37/5}}{{100}} = \frac{?}{{15}} \Rightarrow ? = \frac{{37/5 \times 15}}{{100}} \simeq \frac{{562}}{{100}} = 5/62\)
این کشاورز 5/62 هکتار از زمین خود را جو کاشته است.
پ) سپس مساحت زیر کشت دو قسمت گندم و جو را با هم جمع می کنیم:
6/75+5/62=12/37
ت) مساحت کل زمین را از جمع مساحت قسمت های گندم و جو کم می کنیم تا مساحت قسمت زیر کشت ذرت به دست بیاید:
15 – 12/37 = 2/63
این کشاورز تقریبا 2/63 هکتار از زمین خود را ذرت کاشته است.
4- حاصل عبارت رو به رو را پیدا کنید.
\(1\frac{1}{2} \times 1\frac{1}{3} \times 1\frac{1}{4} \times \cdots \times 1\frac{1}{{100}} = \)
از راهبرد حل ساده تر و الگویابی استفاده می کنیم:
\(1\frac{1}{2} \times 1\frac{1}{3} \times 1\frac{1}{4} \times \cdots \times 1\frac{1}{{100}} = \frac{3}{2} \times \frac{4}{3} \times \frac{5}{4} \times \cdots \times \frac{{101}}{{100}} = \frac{{101}}{2}\)
5- در یک کارگاه تولیدی، 4960 جفت کفش تولید شده که \(\frac{3}{8}\) آنها پسرانه و بقیه دخترانه است.اگر قیمت هر جفت کفش پسرانه 350000 تومان و قیمت هر جفت کفش دخترانه 420000 تومان باشد، درآمد این کارگاه چقدر است؟
از راهبرد زیر مسئله استفاده می کنیم:
الف) ابتدا تعداد کفش های پسرانه را به دست می آوریم:
\(\frac{3}{8} \times \frac{{4960}}{1} = \frac{{14880}}{8} = 1860\)جفت
ب) تعداد کفش های دخترانه را به دست می آوریم:
جفت 3100 = 1860 – 4960
پ) درآمد حاصل از فروش کفش های پسرانه و دخترانه را به دست می آوریم:
درآمد فروش کفش های پسرانه:
\(1860 \times 350,000 = 651,000,000\)تومان
درآمد فروش کفش های دخترانه:
\(3100 \times 420,000 = 1,302,000,000\)تومان
درآمد حاصل برابر خواهد بود با:
\(1,302,000,000 + 650,000,000 = 1,952,000,000\)تومان
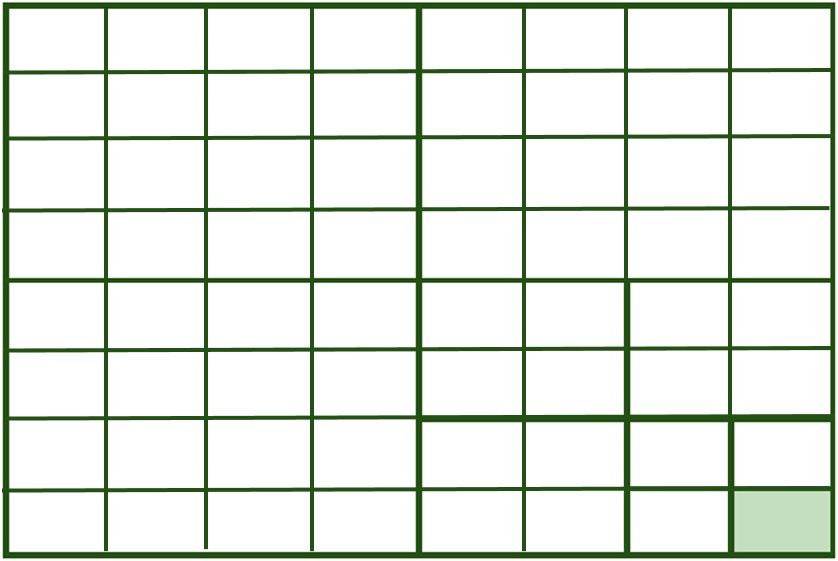
6- سارا یک بازی روی صفحهٔ شطرنجی انجام می دهد.مهرهٔ او روی خانهٔ \(\left[ \begin{array}{l}2\\3\end{array} \right]\) است. او ابتدا مهره اش را 3 خانه به سمت راست، سپس 4 خانه به سمت بالا و در انتها 2 خانه به سمت چپ می برد.در حال حاضر مهرهٔ سارا روی کدام خانه قرار دارد؟
از راهبرد رسم شکل استفاده می کنیم:
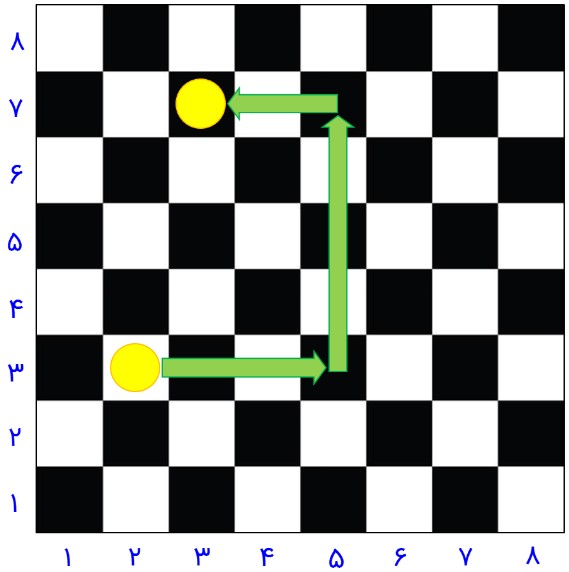
با توجه به پیکان های رسم شده، مشخص است که مهره سارا در حال حاضر بر روی خانه \(\left[ \begin{array}{l}3\\7\end{array} \right]\) قرار دارد.
7- چه کسری از شکل زیر رنگی است؟ توضیح دهید.
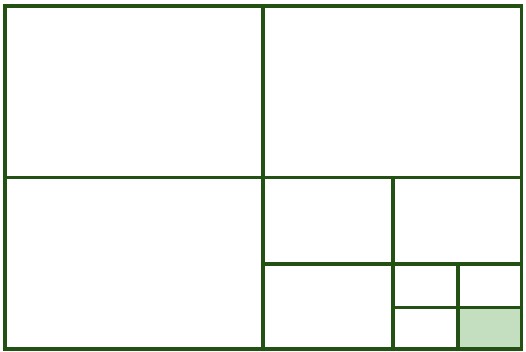
اگر تقسیم شکل را ادامه دهیم، شکل به 64 خانه تقسیم می شود؛ بنابراین \(\frac{1}{{64}}\) شکل رنگی است.
8- اگر دیوارهای یک استخر با طرح زیر، کاشی کاری شده باشد، چه کسری از دیوار، کاشی آبی دارد؟
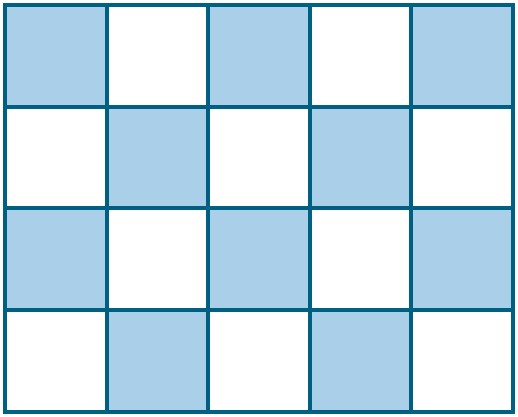
با شمارش کل کاشی ها و نسبت کاشی های آبی به کل کاشی ها، متوجه می شویم که 20 کاشی داریم که 10 تا از آن ها آبی هستند. اگر این نسبت در تمام دیوار رعایت شود، رابطه زیر را خواهیم داشت:
\(\frac{{10}}{{20}} = \frac{1}{2}\)
در نتیجه \(\frac{1}{2}\) دیوار، کاشی آبی دارد.
9- در چند حالت، حاصل ضرب 2 عدد طبیعی، 36 می شود؟ در کدام حالت، حاصل جمع، کمترین مقدار است؟
از راهبرد الگوسازی و حذف حالت های نامطلوب استفاده می کنیم:
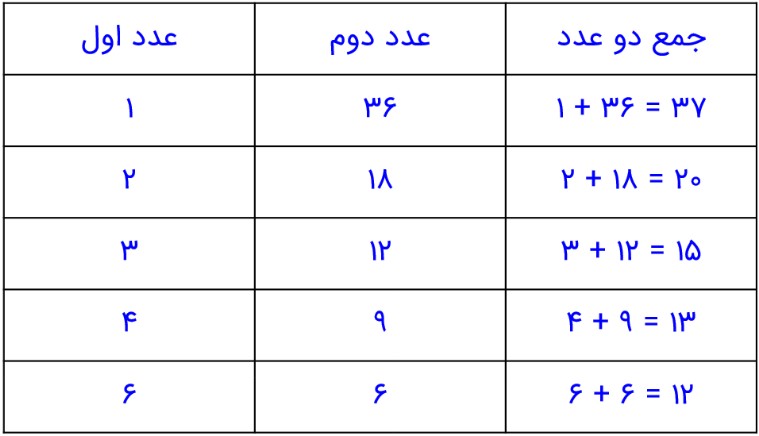
می بینیم که کمترین مجموع، 12 می باشد.
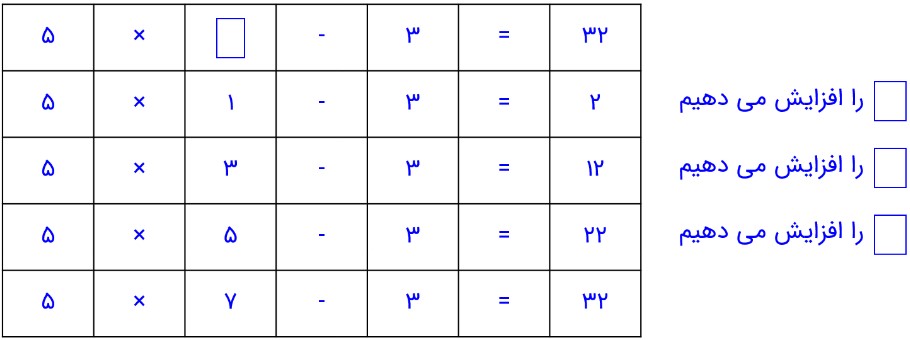
10- عددی را 5 برابر و 3 واحد از آن کم کردیم؛ حاصل، 32 شد. عدد موردنظر چند است؟
از راهبرد حدس و آزمایش استفاده می کنیم:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















