جواب کاردرکلاس صفحه 2 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)

1 به طور شهودی می توان دید که از هر دو نقطهٔ متمایز، تنها یک خط عبور می کند؛ بنابراین:

الف با داشتن مختصات .... نقطه از یک خط باید بتوان معادلهٔ آن را به دست آورد.

ب با داشتن معادلهٔ یک خط می توان با مشخص کردن .... نقطه از خط، نمودار آن را در دستگاه مختصات رسم کرد.

2 نمودار خطوط با معادلات زیر را در دستگاه مختصات مشخص شده، رسم کنید: 

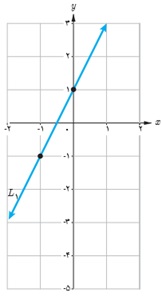
الف \({L_1}\;:\;y = 2x + 1\)

ب \({L_2}\;:\;y = 2x - 3\)

پ \({L_3}\;:\;y = 1\)

ت \({L_4}\;:\;x = - 2\)

ث \({L_5}\;:\;x + 2y = 2\)

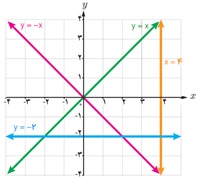
3 معادلهٔ هریک از خط های نمایش داده شده روی شکل را بنویسید.

4 الف می دانیم که شیب یک خط برابر است با نسبت جابه جایی عمودی به جابه جایی ....؛ به عبارت دیگر شیب خط گذرا از دو نقطهٔ غیر هم طول A و B برابر است با:

\({m_{AB}} = \frac{{\;..........\;}}{{{x_B} - {x_A}}}\) 

ب شرط موازی بودن دو خط آن است که دارای ...... برابر باشند.

5 الف از پایهٔ نهم به خاطر داریم که هرگاه خط L محور yها را در نقطه ای با عرض h قطع کند، آن گاه h، .................. خط L نامیده می شود.

ب در سؤال 2، شیب و عرض از مبدأ هریک از پنج خط ذکر شده را بنویسید. در این سؤال کدام دو خط با هم موازی اند؟

6 الف خط با شیب m و عرض از مبدأ h معادله ای به صورت y = …….. دارد.

ب می خواهیم معادلهٔ خط L، گذرا از دو نقطهٔ A(0,7) و B(3,1) را بنویسیم. برای این کار، ابتدا شیب خط را محاسبه می کنیم:

 شیب خط: \(m = \frac{{{y_B} - {y_A}}}{{{x_B} - {x_A}}} = \frac{{1 - 7}}{{3 - 0}} = - 2\)

خط : y = -2x + h

B(3,1) روی خط L واقع است:

1 = -2(3) + h  "  h=7

البته اگر به مختصات نقطهٔ A(0,7) از خط L دقت کنیم، بدون محاسبه متوجه می شویم که عرض از مبدأ این خط h = 7 است. پس:

معادلۀ خط L :

Y = -2x + 7

ب معادلهٔ خط گذرنده از نقطهٔ P(2,-1) را بنویسید؛ به طوری که با خط y = 3x – 4 موازی باشد.