1736019749.png)
جواب کاردرکلاس صفحه 15 درس 1 ریاضی یازدهم تجربی (هندسۀ تحلیلی و جبر)
تعداد بازدید : 78.82Mپاسخ کاردرکلاس صفحه 15 ریاضی یازدهم تجربی
-گام به گام کاردرکلاس صفحه 15 درس هندسۀ تحلیلی و جبر
-کاردرکلاس صفحه 15 درس 1
-شما در حال مشاهده جواب کاردرکلاس صفحه 15 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 تعیین کنید کدام یک از سهمی های زیر ماکزیمم و کدام یک مینیمم دارند. سپس مقدار ماکزیمم یا مینیمم هر یک را مشخص کنید.
الف \(g\left( x \right) = - {\left( {x + 1} \right)^2} + 3\)
ب \(h\left( x \right) = {x^2} - 4x + 9\)
الف \(\begin{array}{l}g\left( x \right) = - {\left( {x + 1} \right)^2} + 3 = \\\\ - \;{x^2} - 2x + 2\\\\ \Rightarrow a = - 1 < 0\end{array}\)
تابع دارای مینیمم است
\( \Rightarrow \left\{ \begin{array}{l}{x_S} = - \frac{b}{{2a}} = - \frac{{ - 2}}{{2\left( { - 1} \right)}} = - 1\\ \Rightarrow {y_S} = g\left( { - 1} \right) = - {\left( { - 1 + 1} \right)^2} + 3 = 3\end{array} \right. \Rightarrow S\left( { - 1\;,\;3} \right)\)
ب \(h\left( x \right) = {x^2} - 4x + 9 \Rightarrow a = 1 > 0\)
تابع دارای ماکزیمم است
\( \Rightarrow \left\{ \begin{array}{l}{x_S} = - \frac{b}{{2a}} = - \frac{{ - \;4}}{{2\left( 1 \right)}} = 2\\ \Rightarrow {y_S} = h\left( { - 2} \right) = {\left( 2 \right)^2} - 4\left( 2 \right) + 9 = 5\end{array} \right. \Rightarrow S\left( {2\;,\;5} \right)\)
2 قرار است در کنار یک رودخانه، محوطه ای مستطیل شکل ایجاد کنیم. برای این کار لازم است سه ضلِع محوطه نرده کشی شود. اگر تنها هزینهٔ نصب 100 متر نرده را در اختیار داشته باشیم، ابعاد مستطیل را طوری تعیین کنید که مساحت آن بیشترین مقدارِ ممکن گردد.
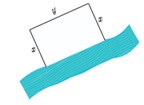
\(\begin{array}{l}y + 2x = 100 \Rightarrow y = 100 - 2x\\S\left( x \right) = y \cdot x = \left( {100 - 2x} \right)x = - \;2{x^2} + 100x \Rightarrow {x_S} = - \frac{b}{{2a}} = - \frac{{100}}{{ - \;4}} = 25 \Rightarrow {y_S} = 50\\ \Rightarrow {S_{\max }} = S\left( {{x_S}} \right) = - \;2{\left( {25} \right)^2} + 100\left( {25} \right) = 1250\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
