1736019749.png)
جواب کاردرکلاس صفحه 39 درس 2 ریاضی یازدهم تجربی (هندسه)
تعداد بازدید : 78.86Mپاسخ کاردرکلاس صفحه 39 ریاضی یازدهم تجربی
-گام به گام کاردرکلاس صفحه 39 درس هندسه
-کاردرکلاس صفحه 39 درس 2
-شما در حال مشاهده جواب کاردرکلاس صفحه 39 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
با توجه به قضیهٔ فیثاغورس اگر زاویهٔ A از مثلثی مانند ABC، قائمه باشد، آنگاه \({a^2} = {b^2} + {c^2}\).
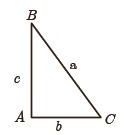
الف عکس این قضیه را بنویسید.
ب با انجام مراحل زیر نتیجه بگیرید که عکس قضیهٔ فیثاغورس نیز درست است.
الف
اگر در مثلث ABC، \({a^2} = {b^2} + {c^2}\) آنگاه مثلث در رأس A قائمه است.
1 فرض کنیم مثلث ABC داده شده است و رابطهٔ \({a^2} = {b^2} + {c^2}\) بین اندازهٔ اضلاع آن برقرار است.
2 پاره خط های \(A'B'\) و \(A'C'\) را مطابق شکل مقابل به گونه ای درنظر بگیرید که \(A'=90°\) و \(A'C'=AC\) و \(A'B'=AB\) است.
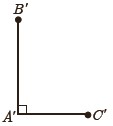
3 با استفاده از قضیهٔ فیثاغورس در مثلث 'A'B'C، اندازه پاره خط 'B'C را به دست آورید و ثابت کنید B'C'=BC.
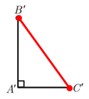
\(\begin{array}{l}B'{{C'}^2} = A'{{C'}^2} + A'{{B'}^2}\\\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \mathop \Rightarrow \limits_{A'C' = b}^{A'B' = c} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B'{{C'}^2} = {b^2} + {c^2}\\\\{a^2} = {b^2} + {c^2}\\\\ \Rightarrow B'{{C'}^2} = {a^2} \Rightarrow B'C' = a\\\\ \Rightarrow B'C' = BC\end{array}\)
4 توضیح دهید چرا \(A\mathop B\limits^\Delta C \cong A'\mathop B\limits^\Delta 'C'\) و نتیجه بگیرید A=90°.
\(\begin{array}{l}\left. {\begin{array}{*{20}{l}}{A'B' = AB}\\{}\\{A'C' = AC}\\{}\\{B'C' = BC}\end{array}} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C'\\\\ \Rightarrow \hat A = \hat A' = {90^\circ }\end{array}\)
ج قضیه فیثاغورس و عکس آن را به صورت یک قضیهٔ دو شرطی بیان کنید.
فرض کنیم ABC یک مثلث باشد:
\({a^2} = {b^2} + {c^2} \Leftrightarrow \hat A = {90^\circ }\)
مثلثی قائم الزاویه است اگر و تنها اگر مربع یک ضلع برابر با مجموع مربع های دو ضلع دیگر باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
