آیا تمام سوالات کاردرکلاس صفحه 66 ریاضی یازدهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به کاردرکلاس صفحه 66 ریاضی یازدهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

گام به گام کاردرکلاس صفحه 66 درس 3 ریاضی یازدهم (تابع)

تعداد بازدید : 54.06M

پاسخ کاردرکلاس صفحه 66 ریاضی یازدهم

گام به گام کاردرکلاس صفحه 66 درس تابع

کاردرکلاس صفحه 66 درس 3

1 توابع f و g را در نظر بگیرید.

\(\begin{array}{l}f = \left\{ {(0\,,\,0)\,,\,(5\,,\,0)\,,\,( - 3\,,\,4)} \right\}\\\\g = \left\{ {(0\,,\,2)\,,\,(1\,,\,\frac{3}{5})\,,\,( - 3\,,\,\frac{2}{7})\,,\,(5\,,\, - 4)} \right\}\end{array}\)

دامنه و ضابطه توابع f+g ، f-g ، f.g ، \(\frac{f}{g}\) و \(\frac{g}{f}\) را به دست آورید.

\(\begin{array}{l}\left\{ \begin{array}{l}{D_f} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\}\\\\{D_g} = \left\{ { - 3\,,\,\,0,\,\,1\,\,,\,\,5} \right\}\end{array} \right.\\\\{D_{f + g}} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\} \Rightarrow f + g = \left\{ {( - 3\,,\,4\frac{2}{7})\,,\,(0\,,\,2)\,,\,(5\,,\, - 4)} \right\}\\\\{D_{f - g}} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\} \Rightarrow f - g = \left\{ {( - 3\,,\,3\frac{5}{7})\,,\,(0\,,\, - 2)\,,\,(5\,,\,4)} \right\}\\\\{D_{f.g}} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\} \Rightarrow f.g = \left\{ {( - 3\,,\,\frac{8}{7})\,,\,(0\,,\,0)\,,\,(5\,,\,0)} \right\}\\\\{D_{\frac{f}{g}}} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\} \Rightarrow \frac{f}{g} = \left\{ {( - 3\,,\,14)\,,\,(0\,,\,0)\,,\,(5\,,\,0)} \right\}\\\\{D_{\frac{g}{f}}} = \left\{ { - 3} \right\} \Rightarrow \frac{g}{f} = \left\{ {( - 3\,,\,\frac{1}{{14}})} \right\}\end{array}\)

توضیح تکمیلی (برای بهتر درک کردن جواب این مسئله):

اول از همه بریم فرمول دامنه مربوط به جمع، تفریق، ضرب و تقسیم دو تابع f و g را بررسی کنیم. اگر دامنه تابع f را با \({D_f}\) و دامنه تابع g را با \({D_g}\) نشون بدهیم، دامنه های توابع جمع، تفریق، ضرب و تقسیم دو تابع f و g به صورت زیر بدست می آیند:

دامنه جمع دو تابع f و g:

\(\begin{array}{l}(f + g)(x) = f(x) + g(x)\\\\{D_{f + g}} = {D_f} \cap {D_g}\end{array}\)

بنابراین ابتدا دامنه جمع دو تابع f و g بدست میاریم و سپس تابع جمع دو تابع را!

دامنه تفریق دو تابع f و g:

\(\begin{array}{l}(f - g)(x) = f(x) - g(x)\\\\{D_{f - g}} = {D_f} \cap {D_g}\end{array}\)

بنابراین ابتدا دامنه تفریق دو تابع f و g بدست میاریم و سپس تابع تفریق دو تابع را!

\(\begin{array}{l}{D_{f - g}} = {D_f} \cap {D_g} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\}\\\\(f - g) = \left\{ {( - 3\,,\,4 - \frac{2}{7})\,,\,(0\,,\,0 - 2)\,,\,(5\,,\,0 - ( - 4))} \right\} = \\\\\left\{ {( - 3\,,\,3\frac{5}{7})\,,\,(0\,,\, - 2)\,,\,(5\,,\,4)} \right\}\end{array}\)

دامنه ضرب دو تابع f و g:

\(\begin{array}{l}(f.g)(x) = f(x) \times g(x)\\\\{D_{f.g}} = {D_f} \cap {D_g}\end{array}\)

بنابراین ابتدا دامنه ضرب دو تابع f و g بدست میاریم و سپس تابع ضرب دو تابع را!

\(\begin{array}{l}{D_{f.g}} = {D_f} \cap {D_g} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\}\\\\(f.g) = \left\{ {( - 3\,,\,4 \times \frac{2}{7})\,,\,(0\,,\,0 \times 2)\,,\,(5\,,\,0 \times ( - 4))} \right\} = \\\\\left\{ {( - 3\,,\,\frac{8}{7})\,,\,(0\,,\,0)\,,\,(5\,,\,0)} \right\}\end{array}\)

دامنه تقسیم دو تابع f و g

\(\begin{array}{l}(\frac{f}{g})(x) = \frac{{f(x)}}{{g(x)}}\\\\{D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {x|g(x) = 0} \right\}\end{array}\)

البته چون هر دو تقسیم رو گفته است، پس بگذارید تا آن دامنه تقسیم دیگری را هم بنویسیم:

\(\begin{array}{l}(\frac{g}{f})(x) = \frac{{g(x)}}{{f(x)}}\\\\{D_{\frac{g}{f}}} = {D_f} \cap {D_g} - \left\{ {x|f(x) = 0} \right\}\end{array}\)

اینجا رو باید توضیحاتش رو زیاد کنیم. چرا؟

بخاطر اینکه یک فرقی بین دامنه تقسیم با دامنه جمع، تفریق و ضرب وجود دارد. فرقش چیست؟

تفاوتش در این است که باید آن دسته از اعضای دامنه که تابع موجود در مخرج کسر را صفر می کند را نیز حذفشان کنیم. ابتدا مسئله را برای تابع \(\frac{f}{g}\) بدست می آوریم:

\(\begin{array}{l}{D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {x|g(x) = 0} \right\} = \\\\\left\{ { - 3\,,\,\,0\,,\,\,5} \right\} - \left\{ {} \right\} = \left\{ { - 3\,,\,\,0\,,\,\,5} \right\}\\\\\frac{f}{g} = \left\{ {( - 3\,,\,\frac{4}{{\frac{2}{7}}})\,,\,(0\,,\,\frac{0}{2})\,,\,(5\,,\,\frac{0}{{ - 4}})} \right\} = \\\\\left\{ {( - 3\,,\,14)\,,\,(0\,,\,0)\,,\,(5\,,\,0)} \right\}\end{array}\)

اگر دقت کنید و به تابع g نگاه بیاندازید، متوجه می شوید که در دامنه ی مشترک بین دو تابع، هیچ عضوی از دامنه تابع g وجود ندارد که مقدار تابع را برابر صفر کند.

اکنون سراغ بدست آوردن دامنه تابع \(\frac{g}{f}\) می کنیم.

\(\begin{array}{l}{D_{\frac{g}{f}}} = {D_f} \cap {D_g} - \left\{ {x|f(x) = 0} \right\} = \\\\\left\{ { - 3\,,\,\,0\,,\,\,5} \right\} - \left\{ {0\,,\,\,5} \right\} = \left\{ { - 3} \right\}\end{array}\)

همین طور که مشاهده می کنید، به ازای دو تا از اعضای تابع f، مقدار این تابع برابر صفر می شود. پس از دامنه ی مشترک بین دو تابع، این دو عضو را باید حذف کنیم. پس از حذف این دو عضو، تنها یک عضو برای دامنه تابع \(\frac{g}{f}\) باقی می ماند. حال سراغ بدست آوردن تابع می کنیم:

\(\frac{g}{f} = \left\{ {( - 3\,,\,\frac{{\frac{2}{7}}}{4})} \right\} = \left\{ {( - 3\,,\,\frac{1}{{14}})} \right\}\)

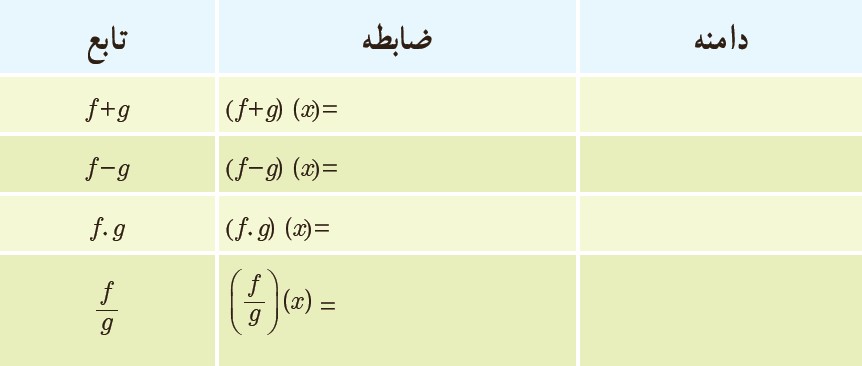
2 برای دو تابع با ضابطه های \(f(x) = {x^2} + 3x + 1\) و \(g(x) = x - 3\) جدول داده شده را کامل کنید.

توضیح تکمیلی (برای بهتر درک کردن جواب این مسئله):

برای توابع جمع، تفریق، ضرب و تقسیم که دو تابع f و g را کافی است که با هم جمع، تفریق، ضرب و تقسیم کنیم. تنها جایی که بایستی مورد بررسی قرار گیرد، دامنه های این توابع هست.

ابتدا سراغ جمع دو تابع می رویم:

\(\left\{ \begin{array}{l}f(x) = {x^2} + 3x + 1 \Rightarrow {D_f} = \mathbb{R}\\\\g(x) = x - 3 \Rightarrow {D_g} = \mathbb{R}\end{array} \right.\)

ساختار توابع f و g چند جمله ای هست و می دانیم که دامنه این نوع توابع همواره \(\mathbb{R}\) خواهد بود. بنابراین داریم:

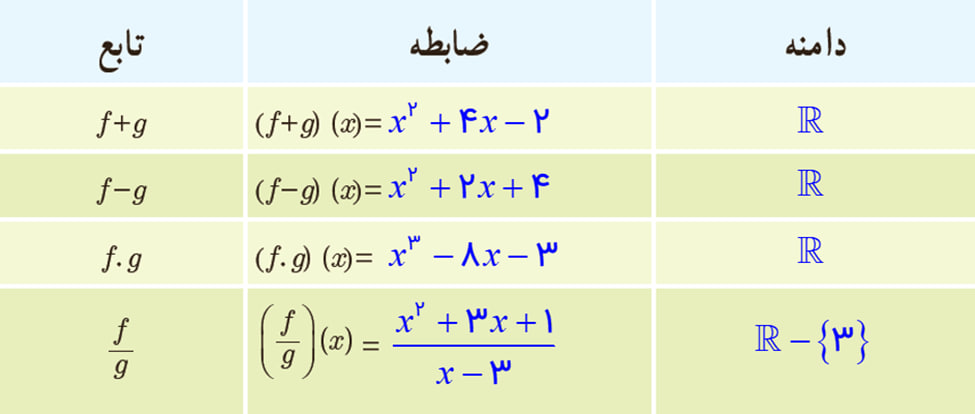
\(\begin{array}{l}(f + g)(x) = f(x) + g(x) = ({x^2} + 3x + 1) + (x - 3) = \\\\{x^2} + 4x - 2\end{array}\)

برای دامنه های توابع جمع، تفریق و ضرب دو تابع هم طبق فرمولی که در سوال 1 نوشتیم، دامنه جمع دو تابع را بدست می آوریم:

\({D_{f + g}} = {D_f} \cap {D_g} = \mathbb{R} \cap \mathbb{R} = \mathbb{R}\)

به همان صورتی که برای جمع دو تابع، مسئله را حل کردیم، سراغ تفریق دو تابع می رویم:

\(\begin{array}{l}(f - g)(x) = f(x) - g(x) = ({x^2} + 3x + 1) - (x - 3) = \\\\{x^2} + 2x + 4\\\\{D_{f - g}} = {D_f} \cap {D_g} = \mathbb{R} \cap \mathbb{R} = \mathbb{R}\end{array}\)

همین روش را برای ضرب دو تابع پیش می رویم:

\(\begin{array}{l}(f.g)(x) = f(x) \times g(x) = ({x^2} + 3x + 1) \times (x - 3) = \\\\{x^3} - 8x - 3\\\\{D_{f.g}} = {D_f} \cap {D_g} = \mathbb{R} \cap \mathbb{R} = \mathbb{R}\end{array}\)

برای تابع تقسیم دو تابع \(\frac{f}{g}\) هم که هر دو تابع را کافی است که بر هم تقسیم کنیم. فقط همان طور که در توضیحات سوال 1 گفتیم، بعد از اشتراک گیری، بایستی آن دسته از x هایی که تابع g را صفر می کنند از جواب بدست آمده از اشتراک گیری دامنه ها را حذف کنیم:

\(\begin{array}{l}(\frac{f}{g})(x) = \frac{{f(x)}}{{g(x)}} = \frac{{{x^2} + 3x + 1}}{{x - 3}}\\\\{D_{\frac{f}{g}}} = {D_f} \cap {D_g} - \left\{ {x|g(x) = 0} \right\} = \mathbb{R} \cap \mathbb{R} - \left\{ {x|x - 3 = 0} \right\} = \\\\\mathbb{R} - \left\{ {x|x = 3} \right\} = \mathbb{R} - \left\{ 3 \right\}\end{array}\)

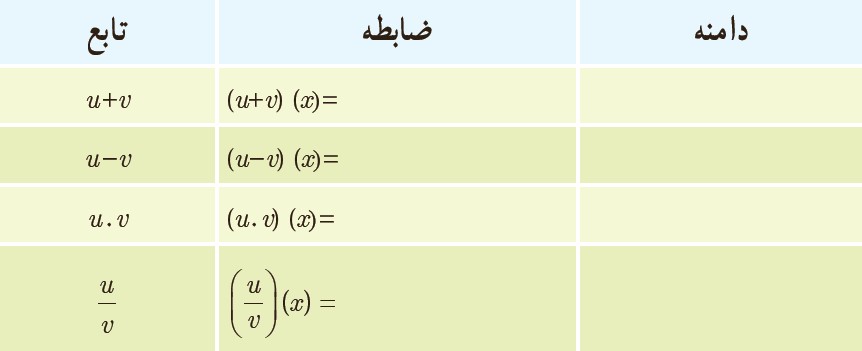
3- برای دو تابع با ضابطه های \(u(x) = \sqrt x + 1\) و \(v(x) = x - 1\) جدول داده شده را کامل کنید.

توضیح تکمیلی (برای بهتر درک کردن جواب این مسئله):

برای توابع جمع، تفریق، ضرب و تقسیم که دو تابع u و v دقیقا مانند همان روشی که در توضیح تکمیلی سوال 2 صحبت کردیم، عمل می کنیم.

دامنه جمع دو تابع f و g:

\(\begin{array}{l}(f + g)(x) = f(x) + g(x)\\\\{D_{f + g}} = {D_f} \cap {D_g}\end{array}\)

ابتدا سراغ جمع دو تابع می رویم:

\(\left\{ \begin{array}{l}u(x) = \sqrt x + 1 \Rightarrow {D_u} = \left[ {0\,,\,\infty } \right)\\\\v(x) = x - 1 \Rightarrow {D_v} = \mathbb{R}\end{array} \right.\)

ساختار تابع v چند جمله ای هست، بنابراین دامنه این تابع برابر \(\mathbb{R}\) خواهد بود. اما تابع u به این علت که یک عبارت \(\sqrt x \) در آن موجود است، دامنه ی آن باید به صورتی باشد که داخل رادیکال همواره بزرگتر مساوی با صفر باشد. بنابراین دامنه این تابع \(\left[ {0\,,\,\infty } \right)\) خواهد بود. داریم:

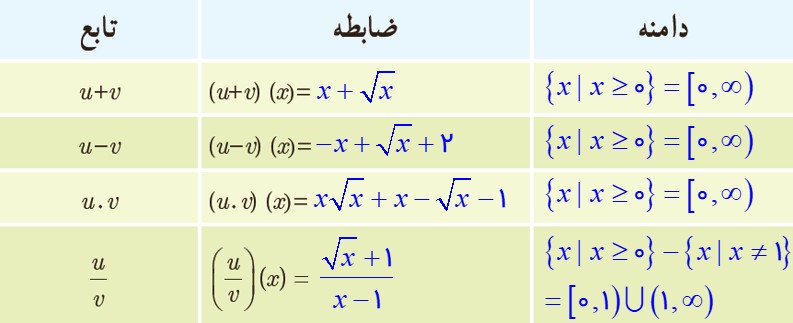
\((u + v)(x) = u(x) + v(x) = (\sqrt x + 1) + (x - 1) = x + \sqrt x \)

\({D_{u + v}} = {D_u} \cap {D_v} = \left[ {0\,,\,\infty } \right) \cap \mathbb{R} = \left[ {0\,,\,\infty } \right)\)

به همان صورتی که برای جمع دو تابع، مسئله را حل کردیم، سراغ تفریق دو تابع می رویم:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\begin{array}{l}(f - g)(x) = f(x) - g(x) = ({x^2} + 3x + 1) - (x - 3) = \\\\{x^2} + 2x + 4\\\\{D_{u - v}} = {D_u} \cap {D_v} = \left[ {0\,,\,\infty } \right) \cap \mathbb{R} = \left[ {0\,,\,\infty } \right)\end{array}\)

همین روش را برای ضرب دو تابع پیش می رویم:

\(\begin{array}{l}(u.v)(x) = u(x) \times v(x) = (\sqrt x + 1) \times (x - 1) = \\\\x\sqrt x + x - \sqrt x - 1\\\\{D_{u.v}} = {D_u} \cap {D_v} = \left[ {0\,,\,\infty } \right) \cap \mathbb{R} = \left[ {0\,,\,\infty } \right)\end{array}\)

برای تابع تقسیم دو تابع \(\frac{u}{v}\) هم که هر دو تابع را کافی است که بر هم تقسیم کنیم. فقط همان طور که در توضیحات سوال 1 گفتیم، بعد از اشتراک گیری، بایستی آن دسته از x هایی که تابع g را صفر می کنند از جواب بدست آمده از اشتراک گیری دامنه ها را حذف کنیم:

\(\begin{array}{l}(\frac{u}{v})(x) = \frac{{u(x)}}{{v(x)}} = \frac{{\sqrt x + 1}}{{x - 1}}\\\\{D_{\frac{u}{v}}} = {D_u} \cap {D_v} - \left\{ {x|v(x) = 0} \right\} = \left[ {0\,,\,\infty } \right) \cap \mathbb{R} - \left\{ {x|x - 1 = 0} \right\} = \\\\\left[ {0\,,\,\infty } \right) - \left\{ {x|x = 1} \right\} = \left[ {0\,,\,\infty } \right) - \left\{ 1 \right\} = \left[ {0\,,\,1} \right) \cup \left( {1\,,\,\infty } \right)\end{array}\)