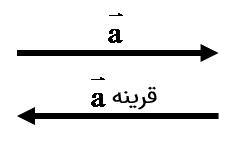
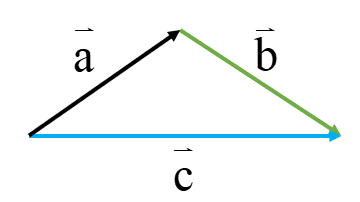
به زودی
این بخش به زودی راه اندازی می شود
به زودی
این بخش به زودی راه اندازی می شود
به وبسایت مای درس خوش آمدید
auto_awesome
grid_view
menu
dashboard
person



1736019749.png)












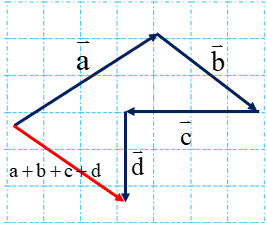
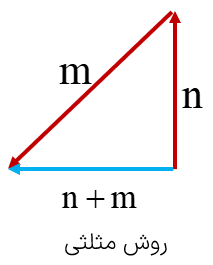
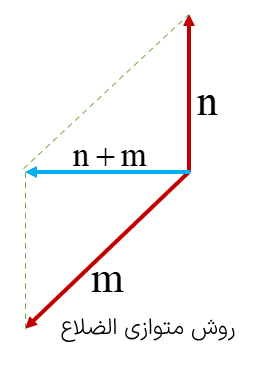
![[شاه کلید مای درس] | جمع بردارها](https://dl.my-dars.com/upload/image/21703947291.png)