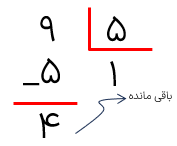
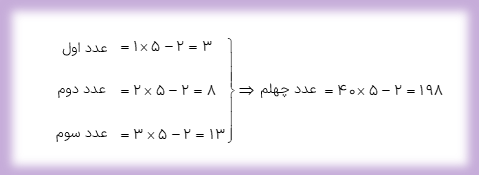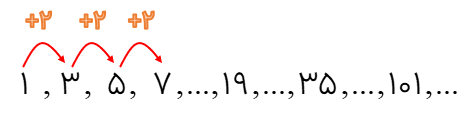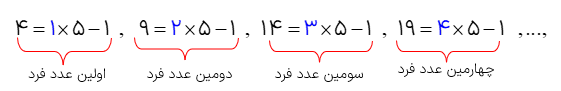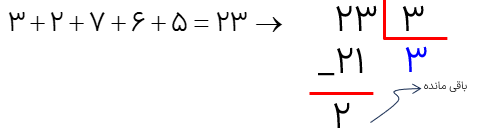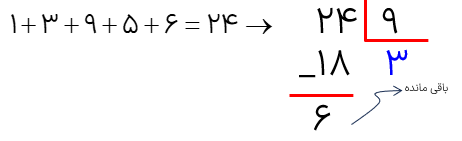درسنامه کامل ریاضی ششم فصل 1 عدد و الگوهای عددی
تعداد بازدید : 7.59Mخلاصه نکات ریاضی ششم فصل 1 عدد و الگوهای عددی - درسنامه شب امتحان ریاضی ششم فصل 1 عدد و الگوهای عددی - جزوه شب امتحان ریاضی ششم نوبت اول فصل 1 عدد و الگوهای عددی
الگوهای عددی
الگوهای عددی
در شکل مقابل ۱۲ ستاره هست آنها را به دسته های دوتایی تقسیم میکنیم همان طور که مشاهده می کنید، تمام ستاره ها در دسته های دوتایی قرار گرفته اند و هیچ ستاره ای باقی نمانده است.
عدد ۱۲، عدد زوج است زیرا اگر ۱۲ تا قلم یا ۱۲ تا دفتر یا ۱۲ تا ستاره داشته باشیم می توانیم آن ها را به دسته های دوتایی تقسیم کنیم، بدون اینکه قلم یا دفتر یا ستارهای خارج از دسته های دوتایی داشته باشیم.
مثال
می دانیم که هر انسان دو دست است. جدول زیر رابطه ی بین تعداد انسان ها و تعداد دست های آن ها را نشان می دهد:
طبق رابطه ای که در جدول بالا وجود دارد می توانیم بنویسیم:
تعداد انسان ها × ۲ = تعداد دست ها
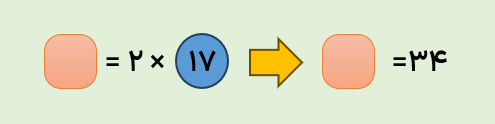
اگر تعداد انسان ها را با دایره و تعداد دست ها را با مربع نشان دهیم، رابطه ی بالا به صورت زیر در می آید.
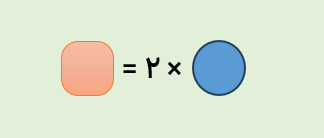
الف انسان روی هم چند دست دارند؟
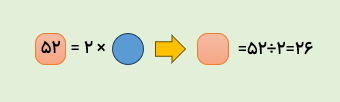
ب52 دست برای چند انسان است؟
به عدد های ... و ۵ و ۴ و ۳ و ۲ و ۱ عددهای طبیعی می گویند.
به عددهای ... و ۱۲ و ۱۰ و ۸ و ۶ و ۴ و ۲ عددهای زوج یا مضرب های عدد ۲ می گویند.
مضرب ۲ یعنی عددی که بر ۲ بخش پذیر است.
از ضرب عددهای طبیعی در عدد ۲ عددهای زوج حاصل می شود.
در عددهایی که بیش از یک رقم ،دارند اگر رقم سمت راست ، عدد ۲,۰، ۴، ۶ یا ۸ ،باشد، به آن عددها، عددهای زوج می گوییم مانند ۷۳۳۴ - ۲۱۸ - ۳۷۵۶
مثال
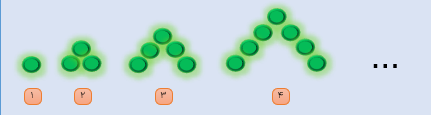
با توجه به الگویی که در شکل زیر هست جدول زیر را کامل کرده ایم.
الف شکل شماره ی ۲۳ دارای چند دایره است؟
23×2-1=45
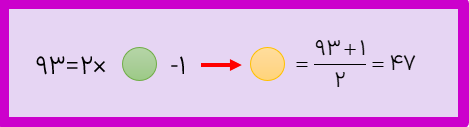
ب شماره ی شکلی که دارای ۹۳ دایره است، چند است؟
1 اگر شماره ی شکل را با مربع و تعداد دایره ها را با دایره نمایش دهیم رابطه ی بین تعداد دایره ها و شماره ی شکل به صورت زیر است.
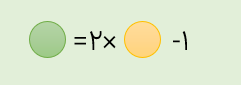
2 به عددهای ... و ۱۱ و ۹ و ۷ و ۵ و ۳ و ۱ عددهای فرد می گوییم. هر عدد طبیعی که زوج نباشد فرد است.
به جدول زیر دقت کنید.

همان طور که می بینید عددهای سطر پایین مضرب های ۳ هستند؛ یعنی عددهایی که بر ۳ بخش پذیرند از ضرب عددهای طبیعی در ۳ مضرب های ۳ حاصل می شوند.
1 عددهای ... و ۲۵ و ۲۰ و ۱۵ و ۱۰ و ۵ را مضرب های ۵ می گویند. مضرب های ۵ بر ۵ بخش پذیر هستند.
2 کوچک ترین مضرب هر عدد، خود آن عدد است.
مثال
به الگوی زیر که با چوب کبریت ساخته شده، دقت کنید.
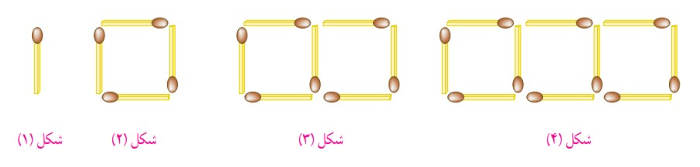
الگوی عددی مقابل تعداد چوب کبریت های شکل بالا را نشان می دهد.
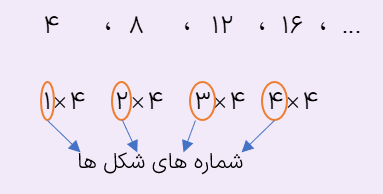
این الگوی عددی مضرب های ۴ را نشان میدهد چون تعداد چوب کبریت های هر شکل ۴ برابر عدد شماره ی آن شکل است، پس بین آن ها تناسب برقرار است.
الف در شکل هفتم چند چوب کبریت وجود دارد؟

به ضرب های مقابل دقت کنید.
۱×۱۲ = ۱2
۲×۶ = ۱۲
۳×۴ =۱۲
با توجه به تساوی های بالا می فهمیم که ۱۲ مضرب عددهای ۱، ۲، ۳، ۴، ۶ و ۱۲ است.
مثال
عدد ۱۸ مضرب چه عددهایی می تواند باشد؟
عدد ۱۸ مضرب عددهای ۱، ۲، ۳، ۶، ۹ و ۱۸ است.
۱ × ۱۸ = ۱۸
۲×۹ = ۱۸
۳×۶ = ۱۸
سه عدد بعدی الگوی عددی زیر را بنویسید و سپس عدد چهلم این الگو را بیابید.
... و ۱۸ و ۱۳ و ۸ و ۳
... و ۳۳ و ۲۸ و ۲۳ و ۱۸ و ۱۳ و ۸ و ۳
چون با اضافه کردن ۵ واحد به هر یک از عددهای الگو عدد بعدی به دست می آید بنابراین اعداد الگو با مضرب های ۵ ارتباط دارند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
الگو یابی
الگویابی
در سال های قبل با مفهوم الگویابی آشنا شده اید و آموختید که الگویابی یکی از ابزارهایی است که می توانیم از آن برای حل یک مسئله استفاده کنیم.
مثال
وسیله ی مقابل ریکشا نام دارد از این وسیله در کشور هند برای جابه جایی مسافران داخل شهر استفاده می شود. همان طور که ملاحظه میکنید این وسیله دارای سه چرخ است. با تشکیل جدول زیر می توانیم رابطه ی بین تعداد ریکشاها و همچنین تعداد چرخ ها را بیابیم.
با دقت در جدول زیر نتیجه میگیریم که هیچ گاه تعداد چرخ ها از ۵ یا ۷ یا ۸ چرخ نمی شود و همواره تعداد چرخ ها باید بر ۳ بخش پذیر باشد.

در مثال بالا به عددهای ۳ و ۶ و ۹ و ... مضرب های عدد ۳ گفته می شود.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
مضرب
مضرب
از ضرب هر عدد طبیعی در عددهای ۱ و ۲ و ۳ و ... مضرب های آن عدد ساخته میشود. بنابراین مضرب های هر عددی همواره بر آن عدد بخش پذیر هستند.
مضرب های7 :\(7 \times 1\,\,,\,7 \times 2\,,\,7 \times 3\,,\,7 \times 4,... \to 7,14,21,28,...\)
مضرب های4 :\(4 \times 1\,,\,4 \times 2\,,\,4 \times 3\,,\,4 \times 4\,,\,...\,,\, \to 4,8,12,16,...\)
.\(20 \times \,1\,,\,20 \times 2\,,\,20 \times 3\,,\,20 \times 4\,,\,...\,,\, \to 20,40,60,80,...\) :مضرب های ۲۰
1 کوچک ترین مضرب هر عددی برابر خود آن عدد و بزرگ ترین مضرب آن عدد، نامعلوم است.
2 عددهای زوج همان مضرب های ۲ هستند.
... و ۸ و ۶ و ۴ و ۲ : عددهای زوج
اعداد زوج و فرد
به الگوی عددی زیر توجه کنید:
به این اعداد عددهای فرد میگوییم با دقت در این عددها ملاحظه می کنید که اگر به هر یک از این عددها ۲ واحد اضافه کنیم عدد بعدی آن به دست می آید؛ یعنی فاصله ی هر عدد با عدد قبل و یا بعد از خودش مساوی ۲ واحد است لذا برای پیدا کردن رابطهی هر عدد فرد و شماره ی آن عدد میتوانیم از مضرب های ۲ کمک بگیریم:
مثال
با توجه به الگوی ،زیر، به سؤالات پاسخ دهید.
الف شکل پنجم چه عددی را نشان میدهد؟
این شکل،ها الگوی عددی روبه رو را نشان می دهند:
.... و ۱۹ و ۱۴ و ۹ و ۴
به هر شکل ۵ مربع اضافه شده تا شکل بعدی آن به دست آمده است. به این ترتیب در شکل پنجم، ۲۴ = ۵ + ۱۹ مربع وجود دارد در این سؤال با توجه به اینکه فاصله ی بین هر عدد با عدد بعد از خودش ۵ واحد است برای پیدا کردن رابطه ی بین هر عدد و شماره ی آن عدد میتوانیم از مضرب های ۵ کمک بگیریم.
ب برای ساختن شکل بیستم به چند عدد توپ نیازمندیم؟
با توجه به رابطه ی بالا برای ساختن شکل بیستم:
۹۹ = ۱- ( ۵ × ۲۰ ) = تعداد توپ ها در شکل بیستم
ج آیا شکلی دقیقا با ۳۰ عدد توپ ساخته می شود؟
با توجه به اینکه عددهای ۴ ,۹ ,۱۴ ,۱۹ و ... همواره یک واحد از مضرب های ۵ کم تر هستند و ۳۰ دقیقا مضرب ۵ است. دقیقا با ۳۰ عدد توپ نمی توان هیچ شکلی با توجه به این الگو ساخت.
1 مجموع دو عدد زوج همواره عددی زوج است.
2 مجموع دو عدد فرد همواره عددی زوج است.
3 مجموع هر عدد زوج با هر عدد فرد همواره عددی فرد است.
عدد نویسی
عدد نویسی
پیش از این با جدول ارزش مکانی آشنا شده اید برای خواندن عدد ۲۰۱۶۱۳۹۴ این عدد را در جدول ارزش مکانی قرار می دهیم.
ارزش مکانی رقم ۲ دهگان میلیون است که در این عدد هشت رقمی بیشترین ارزش مکانی را دارد.
ارزش مکانی رقم ۶ دهگان هزار است.
ارزش مکانی رقم ۳، صدگان است.
هر چه قدر به سمت راست جدول ارزش مکانی حرکت کنیم ارزش مکانی رقم ها کم تر می شود.
عدد ۲۰۱۶۱۳۹۴ خوانده میشود: بیست میلیون و صد و شصت هزار و سیصد و نود و چهار.
مثال
عدد ۹۸۷۶۵۳۴۲۱۰ را به حرف بنویسید.
ابتدا عدد را از سمت راست سه رقم سه رقم دسته بندی میکنیم و سپس با توجه به طبقه ی آن ها، عدد را می خوانیم.
9 ۸۷۶ ۵۳۴ ۲۱۰
نه میلیارد و هشتصد و هفتاد و شش میلیون و پانصد و چهل و سه هزار و دویست و ده.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
گسترده نویسی اعداد
گسترده نویسی اعداد
مثال
گسترده ی عدد 395 را بنویسید.
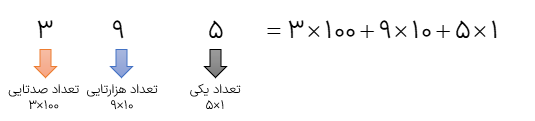
مثال
گسترده ی عدد ۴۹/۱۵۶ را بنویسید.
\(49/156 = 4 \times 10 + 9 \times 1 + 1 \times 0/1 + 6 \times 0/001\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
مقایسه ی عددهای صحیح
مقایسه ی عددهای صحیح
برای مقایسه ی دو عدد، ابتدا به تعداد رقم های آنها توجه میکنیم هر عددی که تعداد رقم هایش بیشتر باشد، بزرگ تر است.
۱۰۰۰۰>۹۸۷۶
در صورت مساوی بودن تعداد رقم ها از اولین رقم سمت چپ رقمی که بیشترین ارزش مکانی را دارد مقایسه را شروع میکنیم و به سمت راست حرکت میکنیم تا به رقمهای دارای ارزش مکانی مساوی و مقدارهای متفاوت برسیم.
مثال
دو عدد ۹۵۰۷۴۹۳ و ۹۵۰۷۵۹۸ را با هم مقایسه کنید.
۹۵۰۷۵۹۸ > ۹۵۰۷۴۹۳
مثال
1 بزرگ ترین عدد چهار رقمی را بنویسید.
۹۹۹۹
2 بزرگ ترین عدد چهار رقمی بدون تکرار رقم ها را بنویسید.
۹۸۷۶ (به ترتیب قرار گرفتن رقم ها دقت کنید)
3 کوچک ترین عدد پنج رقمی را بنویسید.
۱۰۰۰۰
4 کوچکترین عدد پنج رقمی بدون تکرار رقم ها را بنویسید.
۱۰۲۳۴ ( به ترتیب قرار گرفتن رقم ها دقت کنید)
5 با رقم های ۰ و ۱ و ۲ کوچکترین عدد هفت رقمی زوج را بنویسید.
۱۰۰۰۰۰۲
توجه کنید که اگر رقم ۲ غیر از مرتبه ی یکان در هر مرتبه ای قرار می گرفت، دیگر عدد کوچک ترین نمی شد.
جدول ارزش مکانی
جدول ارزش مکانی
در سال های گذشته با نوشتن اعداد به رقم و حروف جایگذاری رقمهای یک عدد در جدول ارزش مکانی وهمچنین خواندن آنها و سپس گسترده نویسی عددها آشنا شدید که در اینجا به یادآوری آن ها می پردازیم.
در این جدول بالاترین ردیف نشان دهنده ی طبقه ی اعداد است. همچنین منظور از حرف ی همان یکان و حرف د همان دهگان و حرف ص همان صدگان می باشد.
در یک جدول ارزش مکانی ممکن است نام طبقه ی یکی ها نوشته نشود.
برای خواندن یک عدد از روی جدول ارزش مکانی کافی است که از بزرگترین طبقه شروع کنیم و عدد مربوط به هر طبقه را نوشته و پس از آن نام طبقه را به همراه یک و بنویسیم در ضمن نام طبقه ی یکی، نوشته نمی شود. به این ترتیب عدد موجود در جدول بالا را به صورت زیر می خوانیم:
بیست و هفت میلیارد و چهار میلیون و شصت و سه هزارو دو «و» سی و چهار هزارم
در عدد بالا بزرگ ترین رقم یکان میلیارد می باشد.
با ارزش ترین رقم هر عدد اولین رقم در سمت چپ آن و کم ارزش ترین رقم هر عدد، اولین عدد سمت راست آن عدد می باشد.
۲۷۰۰۴۰۶۳۰۰۲/۰۳۴
کم ارزش ترین رقم (اولین رقم سمت راست) =4
با ارزش ترین رقم (اولین رقم سمت چپ=2
برای تعیین طبقه یا مرتبه ی یک رقم در یک عدد بهتر است که آن عدد را در یک جدول ارزش مکانی قرار دهیم. البته می توانیم بدون جدول هم این کار را انجام دهیم به این ترتیب که از سمت راست و از یکان عدد سه رقم جدا کنیم و بین قسمت های جدا شده علامت و قرار دهیم تا عدد مربوطه به هر طبقه مشخص شود.
مثال
عدد ۸۳۵۰۰۱۷۳۴۶/۵۲۸۱ را با حروف بنویسید. سپس مرتبه ی هر یک از ارقام ۷، ۴ و ۲ را مشخص کنید.
ابتدا از یکان عدد ( یعنی ۶) به سمت چپ سه رقم سه رقم جدا می کنیم:
\(8350017346/5281 \to 8\,,\,350\,,\,017\,,\,346/5\,,\,281\)
پس عدد فوق را به صورت زیر می نویسیم و می خوانیم:
هشت میلیارد و سیصد و پنجاه میلیون و هفده هزار و سیصد و چهل و شش و پنج هزار و دویست و هشتاد و یک هزارم
رقم ۷ در مرتبه ی یکان طبقه ی ،هزار رقم ۴ در مرتبه ی دهگان طبقه ی یکی و رقم ۲ در مرتبه ی صدم طبقه ی اعشاری قرار دارد.
در نوشتن یک عدد با یک تعداد رقم داده شده رقم صفر نمیتواند با ارزش ترین مکان یعنی اولین رقم سمت چپ عدد قرار بگیرد چون صفر پشت عدد، خوانده نمی شود.
جدول ارزش مکانی مربوط به نمایش یک عدد را میتوانیم به صورت زیر هم نمایش دهیم و با استفاده از این جدول هر عددی را به صورت گسترده ی آن هم بنویسیم به این ترتیب که عدد مورد نظر را در جدول جایگذاری نموده و به ترتیب رقم های آن را با توجه به مرتبهی آنها با هم جمع کنیم دقت داشته باشید که اگر رقم مربوط به یکی از مرتبه،ها صفر ،باشد آن را در گسترده ی عدد نمی نویسیم.
مثال
عدد ۴۳۵۰۷۰۱۸/۰۴۹ را به صورت گسترده بنویسید.
ابتدا عدد را در جدول ارزش مکانی جایگذاری میکنیم و به ترتیب هر رقم را در مرتبه ی آن ضرب نموده و در آخر همگی آن ها با هم جمع می کنیم.
\( \Rightarrow 40000000 + 3000000 + 500000 + 70000 + 10 + 8 + 0/04 + 0/009\) گسترده ی عدد
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
نمایش تقریبی اعداد روی محور
نمایش تقریبی اعداد روی محور
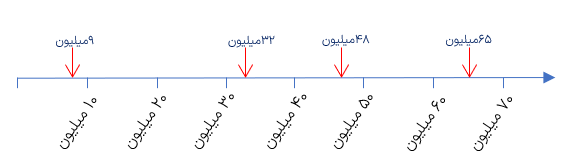
در سال های قبل با نمایش تقریبی اعداد با تقریبهای دهگان صدگان هزارگان و ... آشنا شدید. در این درس می خواهیم شما را با نمایش تقریبی با تقریب های خیلی بزرگ مانند ده میلیون و بزرگ تر از آن آشنا کنیم. به مثال های زیر دقت کنید.
از آن جا که در محور بالا تقریب با رقم دهگان میلیون مورد نظر است برای نمایش عددی مانند ۴۷۸۶۳۷۰۲ بهتر است ابتدا آن را به صورت تقریبی ۴۸۰۰۰۰۰۰ یا همان ۴۸ میلیون بنویسیم سپس محل تقریبی این عدد را با یک فلش روی محور نمایش دهیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
بخش پذیری
بخش پذیری
اگر بخواهیم ۱۴ سیب را بین دو نفر تقسیم کنیم، به هر کدام ۷ سیب میرسد و سیبی باقی نمی ماند. بنابراین میگوییم عدد ۱۴ بر ۲ بخش پذیر است.
اگر ۲۶ شکلات را بین دو نفر تقسیم کنیم به هر یک ۱۳ شکلات میرسد و شکلاتی باقی نمی ماند، بنابراین می گوییم ۲۶ بر ۲ بخش پذیر است.
1 عددی بر ۲ بخش پذیر است که رقم یکان آن 2,0 ، ۴، ۶ یا ۸ باشد.
2 اگر ۱۵ مداد را بین ۵ نفر تقسیم کنیم بر هر کدام ۳ مداد میرسد و مدادی باقی نمی ماند، بنابراین می گوییم ۱۵ بر ۵ بخش پذیر است.
3 اگر ۳۵۰ دفتر را بین ۵ نفر تقسیم کنیم به هر یک ۷۰ دفتر میرسد و دفتری باقی نمی ماند، بنابراین می گوییم عدد ۳۵۰ بر ۵ بخش پذیر است.
4 عددی بر ۵ بخش پذیر است که رقم یکان آن صفر یا ۵ باشد.
5 هر عددی که بر ۲ بخش پذیر باشد، مضرب ۲ است.
6 هر عددی که بر ۵ بخش پذیر باشد، مضرب ۵ است.
7 اگر عددی هم بر ۲ و هم بر ۵ بخش پذیر باشد آن عدد بر ۱۰ بخش پذیر است.
8 رقم یکان اعدادی که هم بر ۲ و هم بر ۵ بخش ،پذیرند یا رقم یکان اعدادی که بر ۱۰ بخش پذیرند، صفر است.
مثال
اعداد مقابل بر ۲ و ۵ بخش پذیرند.
100و 2680 و7530
باقی مانده ی تقسیم یک عدد بر ۲ یا صفر است یا ۱ اگر عدد زوج باشد باقی مانده صفر و اگر عدد فرد باشد، باقی مانده ۱ می شود.
مثال
باقی مانده ی تقسیم اعداد مقابل بر ۲ مساوی ۱ است.
۲۴۶۸۹ و ۹۷۳ و ۱۳۹۵
برای تعیین باقی مانده ی تقسیم یک عدد بر ۵، فقط کافی است که باقی مانده ی تقسیم رقم یکان آن را بر ۵ حساب کنیم.
مثال
باقی مانده ی تقسیم عدد ۱۳۵۹ را بر ۵ حساب کنید
باقی مانده ی تقسیم رقم یکان عدد، یعنی ۹ را بر ۵ حساب می کنیم.
1 عددی بر ۳ بخش پذیر است که جمع رقم هایش بر ۳ بخش پذیر باشد. برای مثال عددهای مقابل بر ۳ بخش پذیرند.
۱۲۳۰ و ۳۰۰۰۰ و ۲۷۹ و ۱۰۰۲
2 عددی بر ۹ بخش پذیر است که مجموع رقم هایش بر ۹ بخش پذیر باشد. برای مثال عددهای مقابل بر ۹ بخش پذیرند.
۱۰۰۹۸ و ۳۱۶۸۷۲ و ۷۰۲۹ و ۱۰۸
برای محاسبه ی باقی مانده ی تقسیم یک عدد بر ۳ ابتدا حاصل جمع رقم های عدد را حساب می کنیم و سپس باقی مانده ی تقسیم این حاصل جمع بر ۳ را به دست می آوریم.
مثال
باقی مانده ی تقسیم عدد ۳۲۷۶۵ را بر3 حساب کنید.
برای محاسبه ی باقی مانده ی تقسیم یک عدد بر ۹ ابتدا حاصل جمع رقمهای عدد را حساب می کنیم و سپس باقی مانده ی تقسیم حاصل جمع را بر ۹ به دست می آوریم.
مثال
باقی مانده ی تقسیم عدد ۱۳۹۵۶ را بر ۹ حساب کنید.
باقی مانده ی تقسیم هر عدد بر ۱۰ برابر است با رقم یکان عدد.
مثال
باقی مانده ی تقسیم عدد ۹۵۳۷ بر ۱۰ برابر است با ۷ و باقی مانده ی تقسیم عدد ۲۰۱۶ بر ۱۰، برابر6 است
1 عددی که هم بر ۲ و هم بر ۳ بخش پذیر باشد بر ۶ نیز بخش پذیر است. برای مثال عددهای مقابل بر ۶ بخش پذیرنده:
2010,108,1536
2 عدد که هم بر ۳ و هم بر ۵ بخش پذیر باشد بر ۱۵ نیز بخش پذیر است. مثال عددهای مقابل بر ۱۵ بخش پذیرند:
۲۱۱۳۵ و ۶۸۱۹۰ و ۲۱۰۰ و ۱۰۵
بخش پذیری بر دو
بخش پذیری بر دو
با توجه به این که هر یک از دسته های ده تایی صدتایی هزارتایی و ... را میتوان همواره به دو قسمت مساوی تقسیم کرد برای بررسی بخش پذیری هر عدد بر ۲ کافی است که یکان آن عدد بر ۲ بخش پذیر باشد؛ یعنی رقم های دهگان صدگان هزارگان و مرتبه های بالاتر تأثیری در بخش پذیری اعداد بر ۲ ندارند. نکته عددی بر ۲ بخش پذیر است که رقم یکان آن ۲۰۰، ۴، ۶ و یا ۸ باشد به عبارت دیگر، تمامی عددهای زوج بر ۲ بخش پذیر هستند.
مثال
کدام یک از عددهای مقابل بر ۲ بخش پذیر هستند؟
۲۴۶۸۰۳ و ۲۴۸۹۵۲ و ۷۲۳۴۸۱۰ و ۲۹۴۵۱ و ۳۵۷۸ و ۳۴۷
یکان عددهای ۳۵۷۸ ، ۷۲۳۴۸۱۰ و ۲۴۸۹۵۲ زوج هستند. پس این اعداد به ۲ بخش پذیرند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
بخش پذیری بر سه
بخش پذیری بر سه
در تقسیم هر بسته ی ده تایی صدتایی هزارتایی و ... بر ، همواره باقی مانده برابر یک است. بنابراین برای تعیین باقی مانده ی تقسیم عددی مانند ۴۵۳ بر ۳ با توجه به این که در این عدد ۴ دسته ی صدتایی، ۵ دسته ی ده تایی و ۳ تا یکی وجود دارد، کافی است که جمع ارقام آن را حساب کرده و بخش پذیری عدد حاصل را بر ۳ بررسی کنیم در صورتی که جمع رقمهای عدد مورد نظر بر ۳ بخش پذیر باشد آن عدد بر ۳ بخش پذیر خواهد شد.
عددی بر ۳ بخش پذیر است که جمع رقم هایش بر ۳ بخش پذیر باشد.
مثال
کدام یک از عددهای زیر بر ۳ بخش پذیر هستند؟
۲۵۸ و ۶۸۹ و ۱۴۳
کافی است که جمع رقم های هر یک از عددها را حساب کنیم عددی بر ۳ بخش پذیر است که جمع رقم های آن بر ۳ بخش پذیر باشد.
8 بر3 بخش پذیر نیست ، پس 143 بر 3 بخش پذیر نیست!
\(143 \Rightarrow 1 + 4 + 3 = 8\)
۲۳ بر ۳ بخش پذیر نیست پس ۶۸۹ بر ۳ بخش پذیر نیست!
\(689 \Rightarrow 6 + 8 + 9 = 23\)
۱۵ بر ۳ بخش پذیر است پس ۲۵۸ بر ۳ بخش پذیر میباشد.
\(258 \Rightarrow 2 + 5 + 8 = 15\)
اگر در بین ارقام ،عددی رقم صفر هم وجود داشته باشد در جمع رقم های آن عدد، نیازی به نوشتن صفر نیست چون مجموع هر عددی با صفر برابر صفر است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
بخش پذیری بر پنج و شش
بخش پذیری بر ۵
با توجه به این که هر یک از دسته های ده ،تایی صدتایی هزارتایی و ... را میتوانیم به ۵ قسمت مساوی تقسیم کنیم برای بررسی بخش پذیری هر عدد بر ۵ کافی است که یکان آن عدد صفر یا ۵ باشد و رقم های دهگان صدگان هزارگان و مرتبه های بالاتر تأثیری در بخش پذیری اعداد بر ۵ ندارند.
عددی بر ۵ بخش پذیر است که رقم یکان آن عدد ۰ یا ۵ باشد.
مثال
در بین اعداد ،زیر کدام یک بر ۵ بخش پذیر هستند؟
۱۹۲۸۳۷۴۶۵و ۳۴۹۷۶۰ و ۵۰۵۰۲ و ۹۸۰ و ۸۸۸۵ و ۵۵۵۸
رقم يكان عددهای ۸۸۸۵، ۹۸۰ ، ۳۴۹۸۶۰ و ۱۹۲۸۳۷۴۶۵ صفر یا ۵ است لذا این عددها بر ۵ بخش پذیرند.
بخش پذیری بر ۶
اعدادی مانند ۱۲، ۱۸، ۲۴ و ... که مضرب های ۶ هستند بر ۶ بخش پذیرند همان طور که ملاحظه می کنید، تمامی این عددها زوج هستند، از طرفی مجموع این عددها نیز بر ۳ بخش پذیرند، در نتیجه تمامی این عددها هم بر ۲ و هم بر ۳ بخش پذیرند.
اعدادی بر ۶ بخش پذیرند که هم بر ۲ و هم بر ۳ بخش پذیر باشند.
مثال
کدام یک از عددهای زیر بر ۶ بخش پذیر هستند؟
۳۰۴۰۵۰ و ۸۰۰۰۲۰ و ۴۵۸۹ و ۷۰۲۰ و ۴۵۰ و ۲۳۶
عدد ۲۳۶ بر ۲ بخش پذیر است اما بر ۳ بخش پذیر نیست ، پس این عدد بر ۶ بخش پذیر نمی باشد.
عدد ۴۵۰ هم بر ۲ و هم بر ۳ بخش پذیر است ، پس این عدد بر ۶ هم بخش پذیر است.
عدد ۷۰۲۰ هم بر ۲ و هم بر ۳ بخش پذیر است ، پس این عدد بر ۶ هم بخش پذیر است.
عدد ۴۵۸۹ عددی فرد است پس بر ۲ بخش پذیر نیست. در نتیجه این عدد نمیتواند بر ۶ بخش پذیر باشد.
عدد ۸۰۰۰۲۰ بر ۳ بخش پذیر نیست ، در نتیجه این عدد نمیتواند بر ۶ بخش پذیر باشد.
عدد ۳۰۴۰۵۰ هم بر ۲ و هم بر ۳ بخش پذیر است در نتیجه این عدد بر ۶ هم بخش پذیر می باشد.
بخش پذیری بر ۹
بخش پذیری بر ۹
در تقسیم هر بسته ی ده تایی صدتایی هزارتایی و ... بر عدد ،۹ همیشه باقی مانده مساوی یک می شود، بنابراین برای تعیین بخش پذیری عددی مانند ۲۰۷ بر ۹ با توجه به این که این عدد دارای دو دسته ی صدتایی و ۷ تا یکی است باید جمع رقمهای این عدد را حساب و بخش پذیری عدد حاصل را بر ۹ بررسی کنیم. نکته عددی بر ۹ بخش پذیر است که جمع رقم هایش بر ۹ بخش پذیر باشد.
مثال
کدام یک از عددهای زیر بر ۹ بخش پذیر است؟
۳۵۴۰۶ و ۲۷۴۹ و ۴۳۲
با توجه به قاعده ی بخش پذیری بر ۹ ابتدا جمع رقمهای هر یک از عددها را حساب می کنیم
\(432 \Rightarrow 4 + 3 + 2 = 9\)
بر ۹ بخش پذیر است در نتیجه ۴۳۲ بر ۹ بخش پذیر است.
\(2749 \Rightarrow 2 + 7 + 4 + 9 = 22\)
۲۲ بر ۹ بخش پذیر نیست. در نتیجه ۲۷۴۹ بر ۹ بخش پذیر نیست.
\(35406 \Rightarrow 3 + 5 + 4 + 6 = 18\)
۱۸ بر ۹ بخش پذیر است. در نتیجه ۳۵۴۰۶ بر ۹ بخش پذیر است.
هر عددی که بر ۹ بخش پذیر باشد حتما بر ۳ هم بخش پذیر است. اما بعضی از عددهایی که بر ۳ بخش پذیرند، بر ۹ بخش پذیر نیستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
بخش پذیری بر ده و پانزده
بخش پذیری بر ۱۰
هر یک از عددهای ۹۳۷۰، ۳۵۸۴۰ و ۱۲۹۳۸۰ که رقم یکان آنها صفر است هم بر ۲ و هم بر ۵ بخش پذیرند. پس این عددها بر ۵×۲ یعنی ۱۰ نیز بخش پذیرند.
1 عددی بر ۱۰ بخش پذیر است که رقم یکان آن صفر باشد.
2 اعدادی که هم بر هم بر ۵ بخش پذیرند، بر ۱۰ هم بخش پذیرند.
بخش پذیری بر ۱۵
اعدادی مانند ۱۵، ۳۰، ۴۵ ۶۰ و ... که مضرب های ۱۵ هستند بر این عدد بخش پذیرند. همان طور که ملاحظه کنید تمامی این عددها هم بر ۳ و هم بر ۵ بخش پذیر هستند.
اعدادی بر ۱۵ بخش پذیرند که هم بر ۳ و هم بر ۵ بخش پذیر باشد.
مثال
کدام یک از عددهای زیر بر ۱۵ بخش پذیرند؟
۴۳۲۵۷۶۰ و ۷۰۲۰۸۰ و ۸۹۴۶ و ۵۶۲۵ و ۲۳۴۰
عدد ۲۳۴۰ هم بر ۵ و هم بر ۳ بخش پذیر است ، در نتیجه این عدد بر ۱۵ هم بخش پذیر می باشد.
عدد ۵۶۲۵ هم بر و هم بر ۳ بخش پذیر است ، در نتیجه این عدد بر ۱۵ هم بخش پذیر می باشد.
عدد ۸۹۴۶ بر ۵ بخش پذیر نیست ، پس این عدد نمیتواند بر ۱۵ بخش پذیر باشد.
عدد ۷۰۲۰۸۰ بر ۳ بخش پذیر نیست ، پس این عدد نمیتواند بر ۱۵ بخش پذیر باشد.
عدد ۴۳۲۵۷۶۰ هم بر ۳ و هم بر ۵ بخش پذیر است ، پس این عدد بر ۱۵ هم بخش پذیر می باشد.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
معرفی اعداد صحیح
معرفی اعداد صحیح
گاهی اوقات شما با جملاتی مانند دمای هوای تهران ۴ درجه بالای صفر است یا دمای هوای اردبیل ۴ درجه زیر صفر است و همچنین ارتفاع تهران از سطح دریا ۱۱۹۰ متر بالاتر است یا ارتفاع دریای بحرالمیت از سطح دریا ۴۲۲ متر پایین تر است مواجه شده اید چه تفاوتی بین دمای بالاتر از صفر یا پایین تر از صفر وجود دارد؟
همان طور که می دانید، مفهوم ۴ درجه بالای صفر با مفهوم ۴ درجه زیر صفر متفاوت است. لذا برای نمایش تفاوت این دو عدد و همچنین ساده و مختصر کردن آنها از علامت های + یا - استفاده کنیم و طبق قرارداد می باید اعدادی که دمای بالاتر از صفر یا ارتفاع بالاتر از سطح دریا را نشان میدهند با علامت + (مثبت)، و اعدادی که دمای پایین تر از صفر و یا ارتفاع پایین تر از سطح دریا را نشان میدهند با علامت – (منفی) نمایش دهیم.
۴- = ۴ درجه زیر صفر
۴+ = ۴ درجه بالای صفر
7متر پایین تر از سطح دریا=-7
۷+ = ۷ متر بالاتر از سطح دریا
دقت داشته باشید که ارتفاع سطح دریا را مساوی صفر در نظر می گیریم.
برای تعیین علامت عددها نیاز داریم که محل مبدأ واحد اندازه گیری و جهت مثبت و منفی را قرارداد کنیم و بر اساس آن عددها را علامت دار کنیم در مثال ارتفاع از سطح دریا سطح دریا را مبدأ در نظر گرفته و ارتفاع آن را مساوی صفر در نظر می گیریم همچنین در مثال دمای هوای نیز خود صفر را به عنوان مبدأ در نظر می گیریم.
عدد صحیح
عددهای ... و ۴ و ۳ و ۲ و ۱ و ۰ و ۱ و ۲- و و ... را عددهای صحیح می نامیم.
اعداد صحیح به سه دسته ی مهم تقسیم می شوند:
۱ اعداد صحیح مثبت که شامل عددهای ۱ و ۲ و ۳+و 4+ و ... می باشند.
۲ عدد صفر که نه مثبت است و نه منفی.
3اعداد صحیح منفی که شامل عددهای 1- و 2- و3- و ۴- و ... می باشند.
محور اعداد صحیح
در ریاضی برای یکی شدن قراردادها و همچنین نمایش عددها روی محور اعداد سمت راست صفر را روی محور مثبت و سمت چپ صفر را منفی در نظر می گیریم.
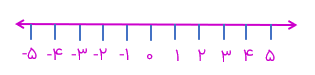
محور اعداد زیر را در نظر بگیرید. نقطه ی مبدأ این محور را با عدد صفر نشان میدهیم. عددهای سمت راست صفر را عددهای صحیح مثبت و عددهای سمت چپ صفر را عددهای صحیح منفی می
نامیم.
1 بزرگ ترین عدد صحیح ،منفی عدد -۱ و کوچک ترین عدد صحیح منفی وجود ندارد.
2 کوچک ترین عدد صحیح ،مثبت عدد ۱ و بزرگترین عدد صحیح مثبت وجود ندارد.)مشخص نیست).
3 علامت هر عدد را در سمت چپ آن قرار میدهیم؛ مانند عدد +7یا ۵- .
7+ را می خوانیم مثبت ۷ و ۵ - را می خوانیم منفی ۵ .
4 در نمایش عددهای مثبت میتوانیم علامت مثبت را ننویسیم، یعنی ۵ = ۵+است.
مقایسه ی عددهای صحیح
بر روی محور اعداد صحیح هر چه به سمت راست یعنی به سمت مثبتها پیش برویم عددها : بزرگ تر می شوند و هر چه به سمت چپ (یعنی به سمت منفی(ها پیش برویم عددها کوچک تر میشوند. بنابراین عدد ۳- از عدد ۵- بزرگ تر است. (۵<۳-) و یا عدد ۱+ از عدد ۱۰۰۰- بزرگ تر است (۱+< ۱۰۰۰-).
پس عددهای صحیح سه دسته هستند: عددهای صحیح مثبت که از صفر بزرگ تر هستند، عددهای صحیح منفی که از صفر کوچک تر هستند و عدد صفر که نه مثبت است و نه منفی.
اعداد صحیح مثبت > صفر > اعداد صحیح منفی
روی محور هر چه در جهت مثبت پیش برویم عددهای بزرگ تر میشوند و هر چه به سمت چپ یعنی در جهت منفی پیش برویم عددها کوچک تر می شوند؛ یعنی:
۱+ 0 <و ۰ > ۴ -و ۲-< ۵۳-
قرینه ی اعداد صحیح
در سال گذشته با مفهوم قرینه نسبت به یک نقطه آشنا شدید در محور زیر اگر بخواهیم قرینه ی عدد ۳+ را نسبت به مبدأ که همان نقطه ی صفر است مشخص کنیم عدد ۳- به دست می آید.
همان طور که ملاحظه می کنید برای قرینه کردن هر عددی نسبت به صفر (مبدأ)، کافی است که علامت آن را تغییر دهیم یعنی علامت مثبت را به منفی و علامت منفی را به مثبت تبدیل کنیم.
اگر عددی علامت نداشته باشد علامت آن مثبت در نظر گرفته میشود یا میتوانیم برای عددهای مثبت، علامت آنها را قرار ندهیم؛ یعنی ۱۷+ = ۱۷ و ۶ = ۶+
فاصله ی عدد ۲+ تا صفر با فاصله ی عدد 2-تا صفر برابر است؛ به همین دلیل عدد 2- را قرینه ی عدد ۲ می گوییم و به همین ترتیب قرینه ی عدد ۱۱ عدد -۱۱ و قرینه ی عدد ۹۳-، عدد ۹۳ است.
1 قرینه ی صفر، خود صفر است.
2 علامت قرینه در ریاضی( _ ) است.
مثال
قرینه 4+ و 9+ را بدست اورید.
4-=(4+)-=قرینه ی4+
-9=قرینه ی+9
هر عددی را که قرینه کنیم علامت آن تغییر می کند.
قرینه ی قرینه ی هر عدد برابر است با خود عدد:
قرینه ی قرینه 5-=\(( - ( - ( - 5))) = - 5\)
قرینه ی قرینه 3+=\( - ( - ( + 3)) = + 3\)



1736019749.png)