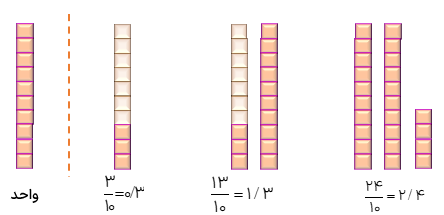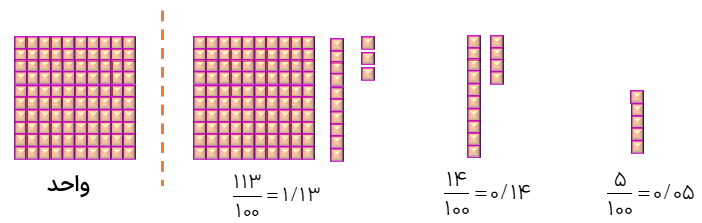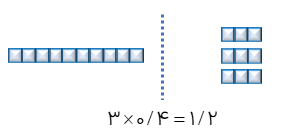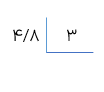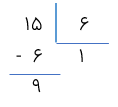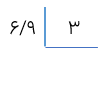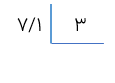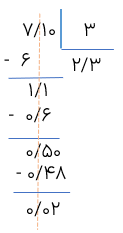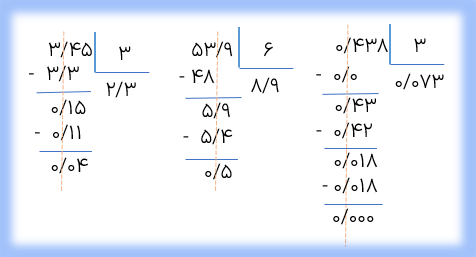درسنامه کامل ریاضی ششم فصل 3 اعداد اعشاری
تعداد بازدید : 7.59Mخلاصه نکات ریاضی ششم فصل 3 اعداد اعشاری - درسنامه شب امتحان ریاضی ششم فصل 3 اعداد اعشاری - جزوه شب امتحان ریاضی ششم نوبت اول فصل 3 اعداد اعشاری
اعداد اعشاری
عدد اعشاری
یادآوری
به کسرهایی که مخرج آنها ۱۰ یا ۱۰۰ یا ۱۰۰۰ و ... باشند کسرهای اعشاری میگویند. کسرهای اعشاری را می توان به صورت عدد اعشاری نوشت.
مثال
کسر اعشاری \(\frac{{273}}{{100}}\) را به صورت عدد اعشاری بنویسید.
\(\frac{{273}}{{100}} = 2/73\)
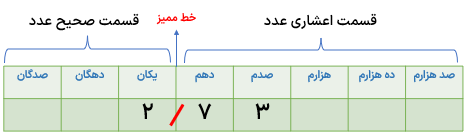
هر عدد اعشاری از دو جزء یا دو قسمت تشکیل شده است جزء صحیح یا قسمت صحیح عدد و جزء اعشاری یا قسمت اعشاری عدد.
برای مثال در عدد ۲/۷۳ داریم:
اگر این عدد را در جدول ارزش مکانی قرار دهیم، به صورت زیر است:
مثال
عدد ۳/۴ را به وسیله ی شکل نمایش دهید.
در این عدد واحد به ۱۰ قسمت مساوی تقسیم شده، یعنی \(1 = \frac{{10}}{{10}}\) واحد.
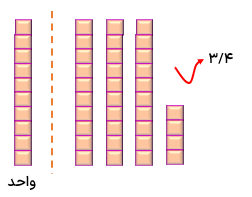
\(3/4 = 3 + 0/4 = 3 + 0/1 + 0/1 + 0/1 + 0/1\)
در سال های قبل با اعداد اعشاری آشنا شدید و دیدید که این اعداد کاربردهای زیادی در زندگی روزمره ی ما و در زمینه های مختلف دارند به طور مثال برای بیان رکوردهای ورزشی از عددهای اعشاری استفاده می شود. همچنین از این اعداد در بیان ، ارتفاع ، وزن نمره ی درسی و ... استفاده می کنیم.
هر عدد اعشاری دارای دو قسمت است:
۱ قسمت صحیح این قسمت در سمت چپ خط اعشار ممیز) قرار میگیرد مانند: ۷۰۴/۰۲۸ یا ۱۳/۶۹
۲ قسمت اعشاری: این قسمت در سمت راست خط اعشار ممیز) قرار میگیرد مانند: ۷۰۴/۰۲۸ یا ۱۳/۶۹
به کسرهایی که مخرج آنها ۱۰، ۱۰۰، ۱۰۰۰ یا ... باشد کسر اعشاری می گویند مانند: \(\frac{{125}}{{1000}}\,\,,\,\,\,\frac{{125}}{{100}}\,\,,\,\,\,\frac{{125}}{{10}}\) کسرهای اعشاری را میتوان به صورت عددهای اعشاری در جدول ارزش مکانی نوشت به این ترتیب کسرهای اعشاری بالا را می توانیم به صورت ۱۳/۵ ۱/۳۵ و ۰/۱۳۵ هم بنویسیم و آنها را به صورت زیر بخوانیم:
۱۳/۵ : سیزده و پنج صدم یا سیزده و نیم
۱/۳۵: یک وسی و پنج صدم
۰/۱۳۵ :صد و سی و پنج هزارم
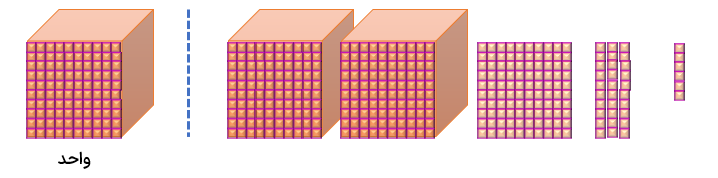
هر عدد اعشاری را میتوان هم با شکل و هم روی محور نمایش داد به شکلهای زیر و عدد اعشاری نمایش داده شده توسط آنها دقت کنید.
مثال
عدد ۲/۱۳۵ را هم با شکل و هم در جدول ارزش مکانی نمایش دهید.
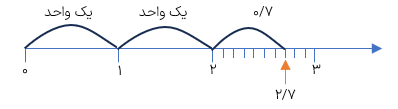
مثال
عدد ۲/۷ را روی محور نمایش دهید.
برای نمایش یک عدد اعشاری مانند ۲/۷ روی محور باید مراحل زیر را انجام دهیم:
۱ محور اعداد را رسم کرده و واحدها را روی آن مشخص کنیم.
۲ به اندازه ی قسمت صحیح عدد اعشاری مورد نظر یعنی ۲ واحد از صفر شروع به شمردن واحدها می
کنیم.
3 با توجه به قسمت اعشاری عدد مورد نظر (که در این جا ۰/۷ است) روی محور بین ۲ و ۳ را به ۱۰ قسمت مساوی تقسیم میکنیم به این ترتیب هر قسمت ۰/۱ میشود پس ۷ تا ۰/۱ شمرده و به جلو می رویم تا نقطه ی نمایش عدد ۲/۷ مشخص شود.
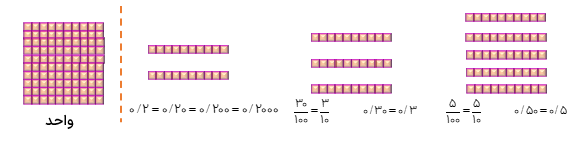
صفر در قسمت اعشاری
به شکل های زیر و تساوی های نوشته شده دقت کنید.
تساوی های بالا نشان میدهند که اگر بعد از آخرین رقم اعشاری هر عددی به تعداد دلخواه صفر قرار دهیم، آن عدد هیچ تغییری نمی.کند از این خاصیت در جمع تفریق و تقسیم عددهای اعشاری استفاده می کنیم. نکته اگر در بین رقم های اعشاری ،عددی صفر قرار دهیم آن عدد تغییر میکند به طور مثال هیچ یک از عددهای ۳/۷۵، ۳/۰۷۵ و ۳/۷۰۵ با یک دیگر برابر نیستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
نوشتن اعداد اعشاری
نوشتن عددهای اعشاری از رقم به حروف
برای خواندن عددهای اعشاری ابتدا قسمت صحیح عدد را مانند عددهای طبیعی معمولی می خوانیم، سپس قسمت اعشاری را نیز مانند عدد صحیح میخوانیم اما با توجه به تعداد رقم های اعشار آن در انتهای عبارت کلمه ی دهم یا صدم یا هزارم و ... را قرار میدهیم برای مثال اگر عدد دارای دو رقم اعشار ،باشد، پس از خواندن قسمت صدم و اگر عدد دارای سه رقم اعشاری باشد پس از خواندن قسمت اعشاری کلمه ی هزارم را به کار می بریم.
مثال
عدد 493/059 را بخوانید. (به حروف بنویسید.)
چهارصد و نود و سه و پنجاه و نه هزارم (چون عدد دارای سه رقم اعشار است).
به روش خواندن این دو عدد دقت کنید.
پنجاه و نه صدم\(0/59 \Rightarrow \)
پنجاه عدد صحیح و نه صدم\(50/09 \Rightarrow \)
اگر عدد قسمت ب را بخواهیم به روش گفته شده بخوانیم ممکن است دچار اشتباه شویم و هر یک از عددهای قسمت الف یا ب را بنویسیم برای جلوگیری از این اشتباه اگر در این گونه موارد عدد صحیح صفر نبود، بعد از خواندن عدد قسمت صحیح، عبارت عدد صحیح را می نویسیم.
مثال
هشتاد و شش هزارم\(0/086 \Rightarrow \)
هشتاد عدد صحیح و شش هزارم\(80/006 \Rightarrow \)
بیست و پنج صدم\(0/25 \Rightarrow \)
بیست عدد صحیح و پنج صدم\(20/05 \Rightarrow \)
نوشتن اعداد اعشاری از حروف به رقم
در این حالت بهتر است از جدول ارزش مکانی استفاده کنیم و هر رقم را در مرتبه ی خودش قرار دهیم.
مثال
عدد صد و سی و چهار و هفتاد و شش صدم را به رقم بنویسید.

نوشتن عددهای اعشاری به صورت کسر
ابتدا كل رقم های عدد را بدون ممیز در صورت کسر قرار میدهیم و سپس در مخرج کسر، عدد ۱ را قرار می دهیم و در سمت راست عدد ۱ به تعداد رقم های اعشار، صفر قرار می دهیم.
مثل عدد ۵۲/۱۹۵ به این صورت میشود:
\(\frac{{52195}}{{1000}}\)
نوشتن کسرها به صورت عددهای اعشاری
الف: اگر مخرج کسر ۱۰ یا ۱۰۰ یا ۱۰۰۰ یا ... باشد، ابتدا عدد صورت کسر را می نویسیم و سپس به تعداد صفرهای مخرج از سمت راست، ممیز می زنیم.
مثال
عدد\(\frac{{4273}}{{1000}}\) را به صورت اعشاری بنویسید.
\(\frac{{4273}}{{1000}} = 4/273\)
اگر مخرج کسر10 یا 100 یا 1000 و00 نبود برای تبدیل کسر به اعشاری ابتدا باید باضرب صورت و مخرج در عدد مناسب مخرج کسر را به ۱۰ یا ۱۰۰ یا ۱۰۰۰ و ۰۰ تبدیل کنیم و سپس کسر اعشاری را به صورت عدد اعشاری بنویسیم برای راحتی کار بهتر است که ضرب های مقابل را به خاطر بسپارید.
2×5=10
4×25=100
8×125=1000
مثال
کسرهای زیر را به عدد اعشاری تبدیل کنید.
\(\begin{array}{l}\frac{3}{5} \Rightarrow \frac{{3 \times 2}}{{5 \times 2}} = \frac{6}{{10}} = 0/6\\\\\frac{{43}}{{25}} \Rightarrow \frac{{43 \times 4}}{{25 \times 4}} = \frac{{172}}{{100}} = 1/72\\\\\frac{{12}}{{125}} \Rightarrow \frac{{12 \times 8}}{{125 \times 8}} = \frac{{96}}{{1000}} = 0/096\end{array}\)
گاهی اوقات ممکن است که نتوانیم مخرج را با ضرب عددها به ۱۰ یا ۱۰۰ یا ۱۰۰۰ تبدیل کنیم و در این صورت یا باید ابتدا در صورت امکان کسر را ساده کنیم و یا اگر این کار ممکن نباشد با تقسیم صورت کسر بر مخرج، آن را به عدد اعشاری تبدیل کنیم.
مثال
عدد \(\frac{{21}}{{12}}\) را به صورت عدد اعشاری بنویسید.
\(\frac{{21 \div 3}}{{12 \div 3}} = \frac{7}{4} = 1\frac{3}{4} \to 1\frac{{3 \times 25}}{{4 \times 25}} = 1\frac{{75}}{{100}} = 1/75\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
مقایسه ی عددهای اعشاری
مقایسه ی عددهای اعشاری
برای مقایسه ی اعداد اعشاری ابتدا قسمت صحیح آنها را مقایسه میکنیم هر عددی که قسمت صحیح آن بزرگ تر باشد، آن عدد بزرگ تر است. اگر قسمتهای صحیح دو عدد مساوی باشند، به ترتیب دهم، صدم و هزارم و ... آن ها را مقایسه میکنیم دهم هر عددی که بزرگ تر بود آن عدد بزرگ تر است و اگر دهم ها نیز مساوی باشند، صدم هر عددی که بزرگ تر باشد آن عدد بزرگ تر است و ....
مثال
\(\begin{array}{l}5/783\,\,\,\,\, > \,\,\,\,\,\,2/9999\\\\0/9876\,\,\,\,\,< \,\,\,\,\,\,1/7\end{array}\)
مثال
عددهای اعشاری زیر را مقایسه می کنیم.
\(9/01\,\,\left\lfloor {\,\,} \right\rfloor \,\,8/9873 \to 9/01 > 8/9873\)
چون عدد صحیح ۹ بزرگ تر از عدد صحیح ۸ است پس عدد ۹/۰۱ از عدد ۸/۹۸۷۳ بزرگ تر است.
\(19/3874\,\,\left\lceil {\,\,} \right\rceil \,\,19/3859 \to 19/3874 > 19/3859\)
چون قسمت های صحیح و رقم های دهم و صدم دو عدد مساوی است بنابراین رقم هزارم آن ها را مقایسه می کنیم.
اگر رقم دهم یک عدد اعشاری کوچک تر از یک از ۴ بیشتر باشد آن عدد از نصف کم تر نیست ( یا مساوی نصف است و یا از نصف بیشتر است) مانند:
بزرگ تر از نصف هستند\(0/6\,\,\,,\,\,\,0/8000002\,\,,\,\,\,0/73 \Rightarrow \)
نصف = ۰/۵۰۰
در صورتی که قسمت صحیح دو عدد برابر بود دهم ها را با هم مقایسه میکنیم عددی بزرگ تر است که دهم آن بزرگ تر باشد.
در صورت تساوی دهم ها باید صدمها را مقایسه کنیم و این عمل را تا جایی ادامه دهیم که عدد بزرگ تر معلوم شود.
\(5/7\,\,\,\, > \,\,\,\,5/37\,\,\,\,\,\,\,\,\,\,\,\,\,13/235\,\,\,\, < \,\,\,\,13/25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7/029\,\,\,\, > \,\,\,\,7/0258\)
مثال
۱۰ کارت با رقم های ۰ تا ۹ و یک کارت با نماد ممیز داریم:
الف اگر عدد ۵۱ را در سمت چپ ممیز بسازیم با ۵ کارت دیگر در قسمت اعشاری (سمت راست ممیز) نزدیک ترین عدد ممکن به ۵۱ را بسازید.

ب اگر عدد ۵۱ را در سمت چپ ممیز بسازیم با ۵ کارت دیگر در قسمت اعشاری (سمت راست ممیز) نزدیک ترین عدد ممکن به ۵۲ را بسازید.
مثال
گسترده عدد اعشاری به چه صورت نمایش داده می شود؟
الف \(52/03 \)
\(52/03 = 50 + 2 + 0/03\)
ب\(412/019 \)
\(412/019 = 400 + 10 + 2 + 0/1 + 0/009\)
جمع و تفریق عددهای اعشاری
جمع و تفریق عددهای اعشاری
در جمع و تفریق عددهای اعشاری باید دقت کنیم که ممیزها خیلی دقیق زیر هم قرار گیرند. به این ترتیب رقم های هم مرتبه نیز زیر هم قرار میگیرند؛ یعنی یکان ها زیر ،هم دهم ها زیر هم صدم ها زیر هم و ...
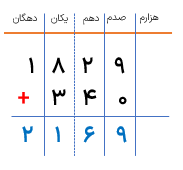
مثال
حاصل جمع و تفریق های زیر را حساب کنید.
18/29+3/4
ابتدا عددها را در جدول ارزش مکانی قرار میدهیم تا رقم های هم مرتبه زیر هم قرار گیرند.
7/1-2/76
در سال قبل با روش های مختلف محاسب هی جمع و تفریق عددهای اعشاری از قبیل رسم شکل، رسم محور، تبدیل به کسر گسترده نویسی و روش جدول ارزش مکانی یا همان زیر هم نویسی آشنا شدید و ملاحظه کردید که روش زیر هم نویسی سریع ترین و ساده ترین روش محاسبه بود در این روش با توجه به ارزش مکانی عددها، باید ممیزها زیر هم و عددهای هم مرتبه ی هم زیر هم نوشته شوند؛ یعنی یکان ها را زیر هم دهم ها را زیر همدیگر و ... بنویسیم سپس از کم ترین مرتبه جمع یا تفریق مورد نظر را انجام دهیم و هر کجا که به ممیز رسیدیم، در جواب هم ممیز را بنویسیم دقت داشته باشید که اگر عددی ممیز نداشته باشد، باید در سمت راست آن ممیز قرار دهیم.
مثال
حاصل جمع ها و تفریق های زیر را بدست آورید.
الف\(5/43 + 17/6\)
\(\begin{array}{l}\,\,\,\,\,\,\,5/43\\ + \,\,\,\,\,17/60\\ - - - - - - - - \\\,\,\,\,\,\,\,\,23/03\end{array}\)
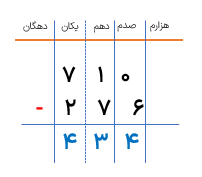
ب\(18 - 5/43\)
\(\begin{array}{l}\,\,\,\,\,\,18/00\\ - \,\,\,\,\,5/43\\ - - - - - - - \\\,\,\,\,\,\,12/57\end{array}\)
ج\(724/5 + 72/45\)
\(\begin{array}{l}\,\,\,\,\,724/50\\ + \,\,\,\,\,72/45\\ - - - - - - - - \\\,\,\,\,\,796/95\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
تبدیل کسر و عدد اعشاری به یکدیگر
تبدیل کسر اعشاری به عدد اعشاری
برای تبدیل کسرهایی مانند \(\frac{{75}}{{10}}\) و\(\frac{3}{{100}}\) و\(\frac{{243}}{{1000}}\) و... که مخرج آن ها ۱۰، ۱۰۰، ۱۰۰۰ و .. می باشد به عدد اعشاری، ابتدا صورت کسر را مینویسیم و به تعداد صفرهای مخرج از سمت راست عدد رقم های اعشاری را جدا کرده و ممیز می زنیم.
\(\frac{{75}}{{10}} = 7/5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{3}{{100}} = 0/03\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{243}}{{1000}} = 0/243\)
در تبدیل کسرهایی مانند ، و که مخرج آن ها ۱۰، ۱۰۰، ۱۰۰۰ و ... نیست) به عدد اعشاری، باید با توجه به تساوی کسرها صورت و مخرج کسر را در عددی ضرب کنیم تا مخرج کسر حاصل یکی از عددهای ۱۰،۱۰۰, 000ا و ... شود و کسر اعشاری به دست آید.
\(\frac{3}{5} = \frac{6}{{10}} = 0/6\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{7}{4} = \frac{{175}}{{100}} = 1/75\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{17}}{{125}} = \frac{{136}}{{1000}} = 0/136\)
تبدیل عدد اعشاری به کسر اعشاری
ابتدا عدد را بدون ممیز در صورت کسر می نویسیم و در مخرج کسر به تعداد رقم های اعشاری عدد، جلوی عدد یک، صفر می گذاریم.
\(37/452 = \frac{{37452}}{{1000}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,892/75 = \frac{{89275}}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,879/6 = \frac{{8796}}{{10}}\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
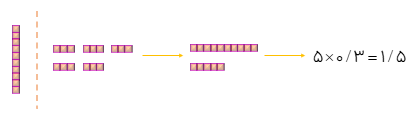
ضرب عددهای اعشاری
ضرب عددهای اعشاری
برای ضرب عددهای اعشاری در حالت کلی ابتدا عددها را بدون در نظر گرفتن ممیز مانند دو عدد صحیح در هم ضرب می کنیم و سپس مجموع تعداد ارقام اعشاری دو عدد را حساب کرده و به همان تعداد از سمت راست در حاصل ضرب اعشار میزنیم.
مثال
حاصل ضرب مقابل را حساب کنید.
۲/۴ × ۱/۵۱
ابتدا حاصل ۱۵۱ × ۲۴ را حساب می کنیم:
۲۴ × ۱۵۱ = ۳۶۲۴
چون دو عدد روی هم سه رقم اعشار دارند بنابراین در حاصل ضرب از سمت راست، سه رقم اعشار می زنیم:
2/4×1/51=3/624
ضرب عددهای اعشاری به وسیله ی تبدیل اعداد اعشاری به کسر
مثال
حاصل ضرب مقابل را حساب کنید.
3/8×2/74
\(3/8 \times 2/74 = \frac{{38}}{{10}} \times \frac{{274}}{{100}} = \frac{{10412}}{{1000}} = 10/412\)
ضرب عددهای اعشاری به وسیله ی شکل
مثال
حاصل ضرب مقابل را به وسیله ی شکل حساب کنید.
5×0/3
مثال
با توجه به واحد حاصل ضرب های زیر را به وسیله ی شکل حساب کنید.
الف0/4×0/7
ب1/5×0/3
۴۵ تا مربع کوچک رنگ شده که هر کدام نشانه ی ۰/۰۱ است.
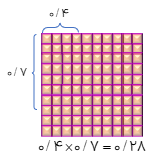
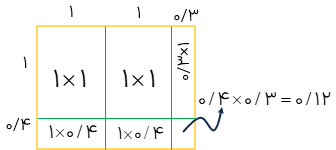
ضرب عددهای اعشاری به کمک مساحت (روش مساحتی)
مثال
حاصل ضرب مقابل را حساب کنید.
1/8×2/3
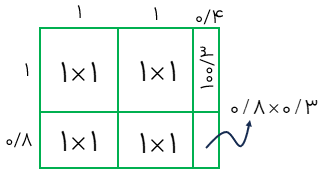
\(\begin{array}{l}1/8 \times 2/3 = (1 \times 1) + (1 \times 1) + (1 \times 0/8) + (1 \times 0/3) + (0/8 \times 0/3)\\ = 1 + 1 + 0/8 + 0/8 + 0/3 + 0/24 = 4/14\end{array}\)
در سال قبل با روش های مختلف محاسبه ی ضرب عددهای اعشاری آشنا شدید در این بخش به یادآوری آن ها می پردازیم.
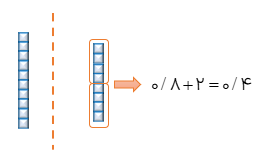
روش اول
برای محاسبه ی حاصل ضرب یک عدد صحیح در یک عدد اعشاری (مانند ۰/۴ × ۳) می توانیم از شکل زیر استفاده کنیم و با شمارش خانه ها مقدار حاصل ضرب را که ۱/۲ می باشد، حساب کنیم.
۳×۰/۴ = ۱/۲
روش دوم (تبدیل به کسر)
در این روش ابتدا اعداد اعشاری را به صورت کسری می نویسیم، سپس حاصل ضرب کسرها را ابتدا بدون ساده کردن آنها به دست می آوریم و در آخر جواب را به صورت اعشاری می نویسیم.
مثال
به مثال های زیر دقت کنید.
الف\(5/3 \times 0/25 = \frac{{53}}{{10}} \times \frac{{25}}{{100}} \times \frac{{1325}}{{1000}} = 1/325\)
ب\(0/2 \times 7/5 \times 12/3 = \frac{2}{{10}} \times \frac{{75}}{{10}} \times \frac{{123}}{{10}} = \frac{{18450}}{{1000}} = 18/450 = 18/45\)
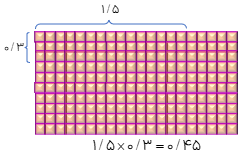
روش سوم (مساحتی)
در این روش برای محاسبه ی حاصل ضرب عددهایی مانند ۲/۳ و ۱/۴، ابتدا یک مستطیل رسم می کنیم طوری که طول مستطیل با عدد بزرگ تر و عرض آن با عدد کوچک تر برابر مستطیل را مانند شکل زیر تقسیم بندی و مساحت تمامی قسمت ها را با هم جمع می باشد. سپس کنیم به این ترتیب حاصل ضرب دو عدد به دست می آید.
مثال
\(\begin{array}{l}2/3 \times 1/4 = (2 \times 1) + (2 \times 0/4) \times 0/3 +0/12\\ = 2 + 0/8 + 0/3 + 0/12 = 3/22\end{array}\)
روش چهارم (فرآیندی):
در این روش ابتدا عددها را بدون در نظر گرفتن ممیزها در یک دیگر ضرب می کنیم سپس به تعداد رقم های اعشاری کل ،عددها در جواب به دست آمده از سمت راست اعشار می زنیم.
الف5/3×0/25=1/325
ابتدا حاصل ضرب ۲۵ × ۵۳ را حساب میکنیم که برابر ۱۳۲۵ می،شود چون ۵/۳ دارای یک رقم اعشاری و ۰/۲۵ هم دارای دو رقم اعشاری است برای جواب ضرب یعنی ۱۳۲۵ از سمت راست سه رقم شمرده و ممیز را می زنیم.
ب\(0/2 \times 7/5 \times 12/3 = 2 \times 75 \times 123 = 18450 \Rightarrow 0/2 \times 7/5 \times 12/3 = 18/450\)
۱ برای ضرب هر عدد اعشاری در عددهای ۱۰، ۱۰۰، ۱۰۰۰ و ... . ابتدا خود عدد را می نویسیم، سپس ممیز را به تعداد صفرها به سمت راست (جلو) انتقال میدهیم یعنی اگر عدد را در ۱۰ ضرب کردیم، باید ممیز را یک رقم به جلو منتقل کنیم و اگر در ۱۰۰ ضرب کردیم باید ممیز را دو رقم به سمت جلو منتقل کنیم و .....
54/327×10=543/27
54/327×100=5432/7
54/327×1000=54327
54/327×10000=543270
۲ اگر هر عدد اعشاری را در ۰/۱۰ ضرب کنیم ممیز آن یک رقم به سمت چپ (عقب) منتقل می شود و اگر در ۰/۰۱ ضرب کنیم، ممیز آن عدد دو رقم به سمت چپ منتقل می شود و ....
54/327×0/1=5/4327
54/327×0/01=0/54327
54/327×0/001=0/054327
54/327×0/0001=0/0054327
تقسیم عددهای اعشاری
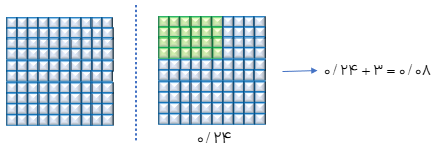
تقسیم عددهای اعشاری به وسیله ی شکل
مثال
حاصل تقسیم مقابل را به وسیله ی شکل حساب کنید.
0/8÷2
مثال
حاصل تقسیم مقابل را به وسیله ی شکل حساب کنید.
0/24÷3
تقسیم اعشاری
برای انجام تقسیم اعشاری بر یک عدد صحیح مانند 1/2÷4 میتوانیم از روش های زیر استفاده کنیم:
روش اول (رسم شکل)
در این روش شکل مربوط به عدد اعشاری را رسم کرده، سپس آن را به قسمت های خواسته شده تقسیم بندی می کنیم.
روش دوم (تبدیل به کسر)
در این روش ابتدا عددهای اعشاری را به صورت کسری می نویسیم، سپس حاصل تقسیم کسرها را به دست می آوریم و در آخر در صورت ،نیاز جواب را به صورت اعشاری می نویسیم.
مثال
\(\begin{array}{l}1)\,\,1/2 \div 4 = \frac{{12}}{{10}} \div 4 = \frac{{12}}{{10}} \times \frac{1}{4} = \frac{3}{{10}} = 0/3\\\\2)\,\,2/97 \div 99 = \frac{{297}}{{100}} \div 99 = \frac{{297}}{{100}} \times \frac{1}{{99}} = \frac{3}{{100}} = 0/03\\\\3)\,\,0/441 \div 7 = \frac{{4441}}{{1000}} \div 7 = \frac{{441}}{{1000}} \times \frac{1}{7} = \frac{{63}}{{1000}} = 0/063\end{array}\)
روش سوم
در این روش تقسیم را مانند یک تقسیم معمولی انجام میدهیم و هرگاه در مقسوم به ممیز رسیدیم در خارج قسمت نیز ممیز میزنیم دقت داشته باشید که در این گونه تقسیم ها، همواره تعداد ارقام اعشاری خارج قسمت و باقی مانده با تعداد ارقام اعشاری مقسوم برابر است.
برای تقسیم هر عدد اعشاری بر عددهای ۱۰، ۱۰۰، ۱۰۰۰ و . .... ابتدا خود عدد را می نویسیم، سپس ممیز را به تعداد صفرها به سمت چپ (عقب) انتقال میدهیم یعنی اگر عدد را بر ۱۰ تقسیم کنیم، باید ممیز را یک رقم به عقب منتقل کنیم و اگر عدد را بر ۱۰۰ تقسیم کنیم باید ممیز را دو رقم به عقب منتقل کنیم و ...
\(\begin{array}{l}794/63 ÷ 10 = 79/463\\794/63 ÷ 100 = 7/9463\\794/63 ÷ 1000 = 0/79463\\794/63 ÷ 10000 = 0/079463\end{array}\)
مثال
حاصل تقسیم مقابل را به کمک شکل حساب کنید.
یادآوری تقسیم
برای اطمینان از درستی عمل تقسیم دو روش برای امتحان آن وجود دارد که به آن ها رابطه های تقسیم میگویند. توجه کنید که حتما باید هر رابطه را برای یک تقسیم بنویسیم و هر دو رابطه درست باشند.
رابطه 1: (خارج قسمت ×مقسوم علیه)+باقی مانده=مقسوم
رابطه 2: باقی مانده<مقسوم علیه
مثال
آیا تقسیم مقابل درست انجام شده است؟
رابطه های تقسیم را می نویسیم:
رابطه ی اول نشان میدهد که تقسیم درست انجام شده است
رابطه 1: 1×6+9=15 رابطه درست است
رابطه 2: غلط است زیرا باقی مانده کوچک تر از مقسوم علیه نیست 9>1
چون باقی مانده از مقسوم علیه کوچک تر نیست پس رابطه ی دوم غلط و در نتیجه تقسیم غلط انجام شده است.
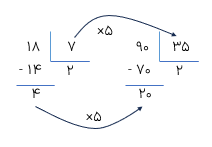
اگر مقسوم و مقسوم علیه تقسیمی را در یک عدد عدد غیر صفر ضرب کنیم خارج قسمت تغییر نمی کند، اما باقی مانده در همان عدد ضرب می شود.
مثال
در تقسیم زیر مقسوم و مقسوم علیه را ۵ برابر کرده ،ایم خارج قسمت تغییر نمیکند، اما باقی مانده ۵ برابر می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
تقسیم عدد اعشاری بر عدد طبیعی
تقسیم عدد اعشاری بر عدد طبیعی
در این حالت باید دقت کنیم که خارج قسمت تقسیم را باید تا چند رقم اعشار انجام دهیم. اگر تعداد رقم های اعشاری خواسته شده ی خارج قسمت بیشتر از تعداد رقم های اعشاری مقسوم ،باشد با قرار دادن صفر در سمت راست رقم های اعشاری ،مقسوم تعداد رقم های اعشاری مقسوم را با تعداد رقم های اعشاری خارج قسمت برابر می کنیم.
مثال
تقسیم مقابل را تا یک رقم اعشار در خارج قسمت انجام دهید.
چون مقسوم دارای یک رقم اعشار است و می خواهیم تقسیم را نیز تا یک رقم اعشار در خارج قسمت انجام دهیم پس نیازی به قراردادن صفر در مقسوم نیست برای دقت در انجام عمل تقسیم و جلوگیری از اشتباه های احتمالی، خط ممیز را رسم می کنیم. خط ممیز نشان دهنده ی ممیز عددها در تمام مراحل تقسیم و از جمله رقم های اعشاری باقی مانده است.
مثال
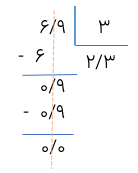
تقسیم مقابل را تا دو رقم اعشار در خارج قسمت انجام دهید و باقی مانده را نیز مشخص کنید.
چون باید تقسیم تا دو رقم اعشار در خارج قسمت انجام شود و مقسوم دارای یک رقم اعشار است. پس یک صفر در سمت راست رقم یک قرار تا مقسوم هم دارای دو رقم اعشار شود.
1 هنگامی که رقم ۱ را پایین می آوریم چون رقم ۱، رقم بعد از ممیز در مقسوم است، به همین دلیل در خارج قسمت ممیز می زنیم و تقسیم را ادامه می دهیم.
2 تعداد رقم های اعشاری باقی مانده با تعداد رقم های اعشاری مقسوم، باید برابر باشد.
تقسیم به کمک رسم شکل
برای تقسیم عددی اعشاری مانند ۴/۴۷ بر ۳ به صورت زیر عمل می کنیم:
ابتدا با توجه به این که کوچک ترین مرتبه ی این عدد صدم میباشد پس هر واحد را به صد قسمت مساوی تقسیم می کنیم و شکل مربوط به این عدد اعشای را رسم میکنیم.
حالا سه تا از واحدهای کامل را انتخاب میکنیم و به هر دسته یک واحد میدهیم یکی از واحدهای کامل باقی ماند که باید آن را باز کنیم و به ده تا ۰/۱ تبدیل کنیم به این ترتیب ۱۴ تا ۰/۱ به وجود می آید. این ۱۴ تا ۰/۱ را به سه قسمت مساوی تقسیم میکنیم که دو تا ۰/۱ باقی می ماند.
حالا دو دسته ۰/۱ باقی مانده را نیز باز میکنیم به این ترتیب ۲۷ تا ۰/۰۱ باقی می ماند که باید آن را به سه قسمت مساوی تقسیم کنیم.
در اخر ملاحظه می کنید که اگر 4/74 را به سه قسمت مساوی تقسیم کنیم هر قسمت مساوی 1/4 خواهد شد.
تقسیم به روش محاسباتی
در این روش ابتدا خط ممیز را رسم میکنیم این خط نشان دهنده ی تمام ممیزهایی است که در انجام تقسیم در عددها قرار میگیرد سپس تقسیم را مانند تقسیم معمولی انجام میدهیم و هرگاه در مقسوم به ممیز رسیدیم، در خارج قسمت هم ممیز میزنیم. دقت داشته باشید که در این گونه تقسیم،ها همواره تعداد ارقام اعشاری خارج قسمت و باقی مانده با تعداد ارقام اعشاری مقسوم برابر است.
مثال
به تقسیم های زیر دقت کنید.
پیشروی در تقسیم
گاهی اوقات برای آن که جواب دقیق تری از تقسیم به دست آید می توانیم در سمت راست قسمت اعشاری مقسوم به تعداد مورد نیاز صفر قرار داده و تقسیم کردن را ادامه دهیم به این ترتیب خارج قسمت دقیق تری به دست می آید. در اصطلاح به این عمل پیشروی در تقسیم می گوییم.
مثال
به تقسیم های زیر دقت کنید.
مثال
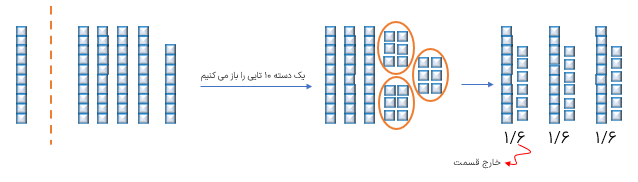
ضخامت کتابی ۲۵۰ صفحه ای ۱/۵ سانتی متر است. ضخامت هر برگ این کتاب چند سانتی متر است؟
دقت داشته باشید که ۲۵۰ صفحه یعنی ۱۲۵ برگ هر برگ دو صفحه است کافی است که عدد ۱/۵ را بر ۱۲۵ تقسیم کنیم و با پیشروی در تقسیم، به باقی ماندهی صفر برسیم که ضخامت هر ورق آن ۰/۰۱۲ سانتی متر می شود.
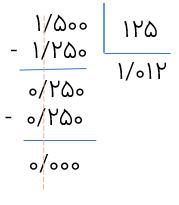
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
تقسیم یک عدد بر عدد اعشاری
تقسیم یک عدد بر عدد اعشاری
در این نوع تقسیم ها ابتدا باید مقسوم و مقسوم علیه را در یکی از اعداد ۱۰ یا ۱۰۰ یا ۱۰۰۰ ضرب کنیم (باتوجه به تعداد رقم های اعشاری مقسوم علیه) تا مقسوم علیه به عدد طبیعی تبدیل شود و سپس باید مانند تقسیم عدد اعشاری بر عدد ،طبیعی تقسیم را انجام دهیم فقط باید دقت کنیم که این تقسیم، تقسیم اصلی نیست تقسیم کمکی است. خارج قسمت تقسیم ،اصلی با خارج قسمت تقسیم کمکی برابر است، اما برای تعیین باقی مانده ی تقسیم ،اصلی باید باقی مانده ی تقسیم کمکی را بر همان عددی که مقسوم و مقسوم عیله در آن ضرب شده، تقسیم کنیم.
مثال
تقسیم مقابل را انجام دهید و باقی مانده را مشخص کنید.
1/4÷0/03
ابتدا مقسوم و مقسوم علیه را در عدد ۱۰۰ ضرب می کنیم تا مقسوم علیه به عدد صحیح تبدیل شود. (توجه کنید که با این کار باقی ماندهی تقسیم نیز ۱۰۰ برابر می شود.)
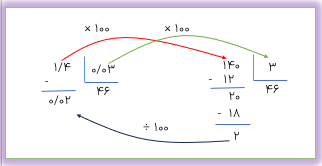
خارج قسمت تقسیم اصلی همیشه با خارج قسمت تقسیم کمکی برابر است برای تعیین تعداد رقم های اعشاری باقی مانده ی اصلی میتوان از روش ساده تری نیز استفاده کرد به این ترتیب که تعداد رقم های اعشاری باقی مانده ی تقسیم با مجموع تعداد رقم های اعشاری مقسوم علیه و خارج قسمت برابر است.
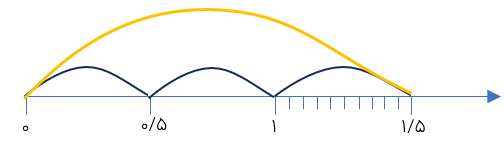
مثال
حاصل تقسیم مقابل را با محور حساب کنید.
1/5÷3
چون مقسوم علیه ۰/۵ است هر واحد را به دو قسمت تقسیم می کنیم.
مثال
حاصل تقسیم مقابل را با محور حساب کنید.
\(3 \div 0/25 \)
چون مقسوم علیه ۰/۲۵ است \((0/25 = \frac{1}{4})\) هر واحد را به چهار قسمت تقسیم می کنیم.
\(3 \div 0/25 = 12\)

همان طور که ملاحظه میکنید اگر مقسوم و مقسوم علیه تقسیمی را در عددی غیر از صفر ضرب کنیم، خارج قسمت تغییر نمیکند اما باقی مانده نیز در همان عدد ضرب می شود.
با توجه به خاصیت بالا میتوانیم تقسیم هایی را که مقسوم علیه اعشاری دارند به تقسیمی که مقسوم علیه طبیعی دارند، تبدیل کنیم کافی است که با توجه به تعداد ارقام اعشاری مقسوم علیه هم مقسوم و هم مقسوم علیه را در یکی از عددهای ۱۰، ۱۰۰، ۱۰۰۰ و ضرب کنیم
به این ترتیب، ممیز مقسوم علیه از بین میرود و به عدد صحیح تبدیل میشود و تقسیم به صورت تقسیم درس قبل تبدیل می شود و میتوانیم به سادگی حاصل تقسیم را به دست آوریم.
اگر مقسوم و مقسوم علیه را در ۱۰ ضرب کنیم باقی مانده هم ده برابر میشود و اگر در ۱۰۰ ضرب کنیم، باقی مانده هم صد برابر میشود لذا برای تعیین باقی مانده ی اصلی تقسیم باید باقی مانده ی به دست آمده را بر همان عددی که مقسوم و مقسوم علیه را در آن ضرب کردیم (یعنی ۱۰، ۱۰۰، ۱۰۰۰ و ..) تقسیم کنیم.
مثال
تقسیم مقابل را انجام دهید.
1/3÷0/07
چون کوچک ترین مرتبه ی مقسوم علیه یعنی ،۰/۰۷ صدم ،بود برای تبدیل ۰/۰۷ به عدد صحیح باید ضرب در صد شود.
مثال
حاصل تقسیم 0/07÷5 را تا یک رقم اعشار در خارج قسمت به دست آورید.
مثال
به کمک ماشین حساب خارج قسمت تقسیم ۰/۷۲ ÷۵/۳ را تا دو رقم اعشار به دست آورید و بدون محاسبه ی تقسیم باقی مانده ی آن را تعیین کنید.
با استفاده از ماشین حساب حاصل تقسیم ۵/۳ بر ۰/۷۲ تا دو رقم اعشار برابر ۷/۳۶ خواهد شد. حالا با استفاده از رابطه ی تقسیم زیر میتوانیم مقدار باقی مانده را به دست آوریم
(مقسوم علیه× خارج قسمت) – مقسوم= باقی مانده
باقی مانده+ (مقسوم علیه× خارج قسمت) = مقسوم
باقی مانده ی تقسیم=\(5/3 - (7/36 \times 0/72) = 5/3 - 5/2992 = 0/0008\)
انجام تقسیم با روش تبدیل به کسر
انجام تقسیم با روش تبدیل به کسر
اگر مقسوم علیه تقسیمی عدد اعشاری ،باشد میتوانیم عدد اعشاری را به صورت کسری بنویسیم و با انجام تقسیم کسرها، حاصل تقسیم را به دست آوریم.
مثال
تقسیم های زیر را به روش تبدیل به کسر انجام دهید.
الف\(0/34 \div 1/7\)
\(0/34 \div 1/7 = \frac{{34}}{{100}} \div \frac{{17}}{{10}} = \frac{{34}}{{100}} \times \frac{{10}}{{17}} = \frac{2}{{10}} = 0/2\)
\(4 \div 0/08\) ب
\(4 \div 0/08 = 4 \div \frac{8}{{100}} = \frac{3}{1} \times \frac{{100}}{8} = \frac{{100}}{2} = 50\)
اگر صورت و مخرج کسری را در عددی (غیر از صفر) ضرب کنیم کسر حاصل با کسر اولیه برابر است.
\(\frac{3}{5} = \frac{6}{{10}} = \frac{9}{{15}} = \frac{{12}}{{20}} = \frac{{15}}{{25}} = ....\)
مثال
الف\(\frac{{{{0/34}_{ \times 100}}}}{{{{1/7}_{ \times 100}}}} = \frac{{{{34}_{ \div 17}}}}{{{{170}_{ \div 17}}}} = \frac{2}{{10}}\)
ب\(\frac{{{4_{ \times 100}}}}{{{{0/08}_{ \times 100}}}} = \frac{{400}}{8} = 50\)
ج\(\frac{{{{7/2}_{ \times 100}}}}{{{{0/06}_{ \times 100}}}} = \frac{{720}}{6} = 120\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم



1736019749.png)