درسنامه کامل ریاضی ششم فصل 4 تقارن و مختصات
تعداد بازدید : 7.59Mخلاصه نکات ریاضی ششم فصل 4 تقارن و مختصات - درسنامه شب امتحان ریاضی ششم فصل 4 تقارن و مختصات - جزوه شب امتحان ریاضی ششم نوبت اول فصل 4 تقارن و مختصات
مرکز تقارن و تقارن مرکزی
تقارن مرکزی
1 تقارن یا قرینه یابی نسبت به یک نقطه را تقارن مرکزی می گویند.
2 در تقارن مرکزی شکل به اندازه ی نیم دور (۱۸۰ درجه) حول (دور) نقطه ی داده شده می چرخد.
مثال
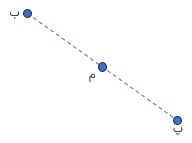
قرینه ی نقطه ی (ب) را نسبت به نقطه ی (م) به صورت زیر است:
با خط کش از نقطه ی «ب» به نقطه ی «م» وصل می کنیم و سپس پاره خط «م ب» را به اندازه ی خودش ادامه می دهیم تا نقطه ی «پ» به دست آید. نقطه ی «پ» قرینه ی نقطه ی «ب» نسبت به نقطه ی «م» است.
در صفحات شطرنجی بدون استفاده از خط کش نیز میتوان قرینه ی یک نقطه را نسبت به نقطه دیگر یافت.
مثال
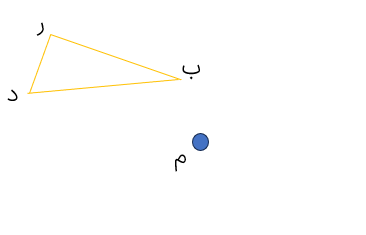
قرینه ی نقطه ی «ر» را نسبت به نقطه ی «م» بیابید.
نقطه ی «ز» قرینه ی نقطه ی «ر» نسبت به نقطه ی «م» است.
مثال
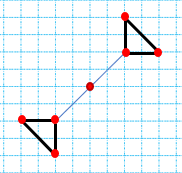
قرینه ی شکل مقابل را نسبت به نقطه ی «م» رسم کنید.
به وسیله ی خط کش قرینه ی هر یک از نقطه های «ز» و «ب» و «د» را نسبت به نقطه ی «م» پیدا کرده و آنها را به هم وصل می کنیم.
اگر نقطه ای مانند م» در داخل یک شکل وجود داشته باشد که قرینه ی هر نقطه روی محیط شکل، نسبت به نقطه ی «م» نقطه ای روی محیط باشد. گوییم نقطه ی «م» مرکز تقارن شکل است.
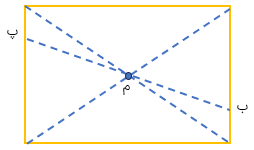
اگر مستطیل را ۱۸۰ درجه حول (دور) نقطه ی «م» بچرخانیم روی خودش منطبق می شود.
نقطه ی برخورد قطرهای مستطیل مرکز تقارن مستطیل است یعنی مستطیل تقارن مرکزی دارد.
در تقارن مرکزی اگر بخواهیم مرکز تقارن یک شکل و قرینه اش را بیابیم باید دو نقطه از شکل را مشخص کنیم و هر نقطه را توسط یک پاره خط به قرینه اش وصل کنیم نقطه ی برخورد دو پاره خط، مرکز تقارن است.
مثال
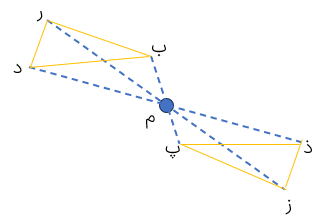
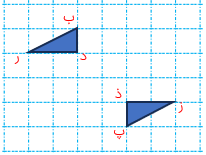
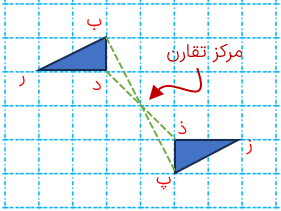
در شکل مقابل مثلث (ب د ر) را ۱۸۰ درجه دوران داده ایم مرکز تقارن را بیابید.
نقطه ی «ب» را به قرینه اش یعنی: نقطه ی «پ» و نقطه ی «د» را به قرینه اش یعنی نقطه «ذ» وصل می کنیم محل برخورد دو پاره خط مرکز تقارن است.
1 اگر شکلی دارای دو خط تقارن محور تقارن عمود برهم ،باشد نقطه ی برخورد دو خط تقارن مرکز تقارن شکل است.
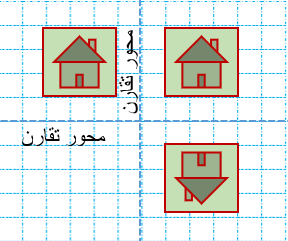
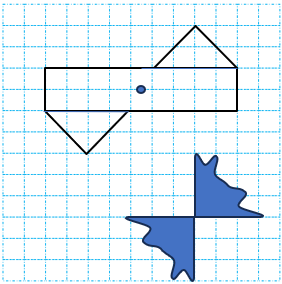
2 بعضی از شکلها خط تقارن محور تقارن ندارند اما مرکز تقارن دارند برای مثال شکل های زیر محور تقارن ندارند اما مرکز تقارن دارند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
یافتن قرینه نقاط مختصاتی
یافتن قرینه نقاط مختصاتی
در سال گذشته با تقارن مرکزی آشنا شدید و آموختید که اگر بخواهیم قرینه ی نقطه ای مانند «آ» را نسبت به نقطه ی «م» به دست آوریم ابتدا به وسیله ی خط کش این دو نقطه را به هم وصل می کنیم و در طرف دیگر به همان اندازه ادامه میدهیم تا به قرینه ی «آ» برسیم. اگر بخواهیم قرینه ی یک شکل را نسبت به یک نقطه رسم کنیم میتوانیم از روشهای زیر استفاده کنیم.
۱- استفاده از کاغذ شفاف
در این روش ابتدا کاغذ شفاف را روی شکل مورد نظر قرار داده و آن شکل را رسم می کنیم، سپس نوک مداد را روی نقطه ای که می خواهیم قرینه ی شکل را نسبت به آن رسم می گذاریم و کاغذ شفاف را ۱۸۰ درجه (نیم دور) حول آن نقطه می چرخانیم به این ترتیب قرینه ی شکل نسبت به نقطه رسم می شود.
2- جابه جایی نقاط شکل
برای رسم قرینه ی یک شکل نسبت به یک نقطه ابتدا قرینه ی رأس های آن شکل را نسبت به نقطه ی مورد نظر مشخص می کنیم نقاط به دست آمده را مانند شکل اصلی به یک دیگر وصل میکنیم برای مشخص کردن قرینه ی هر رأس کافی است که آن رأس را به وسیله خط کش به نقطه ی مورد نظر وصل کنیم و در طرف دیگر آن نقطه به همان اندازه امتداد دهیم.
3- استفاده از محور تقارن
ابتدا روی نقطه ی مورد نظر یک محور افقی و یک محور عمودی رسم میکنیم سپس قرینه ی شکل را ابتدا نسبت به محور عمودی رسم می کنیم تا شکل (۱) به دست آید و بعد قرینه ی شکل (۱) را نسبت به محور افقی رسم میکنیم تا شکل (۲) که همان قرینه ی شکل اصلی نسبت به نقطه ی «م» می باشد، به دست آید.
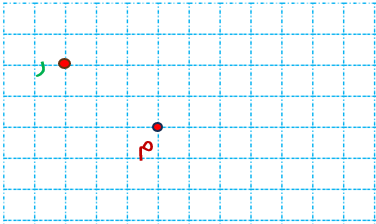
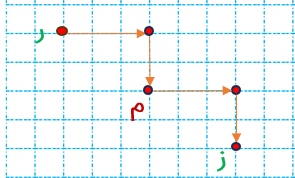
۴- انتقال نقاط روی صفحه ی شطرنجی:
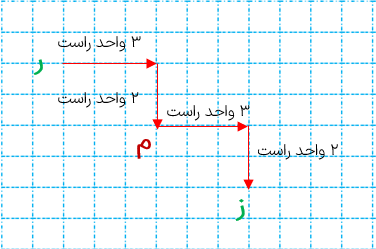
در این روش باید جابه جایی هر رأس را تا نقطه ی مورد نظر، ابتدا به صورت افقی و سپس عمودی بررسی کنیم سپس از آن نقطه مجدداً به همان جهت قبلی ابتدا افقی و سپس عمودی حرکت کنیم به این ترتیب قرینه ی هر رأس نسبت به نقطه ی مورد نظر مشخص می شود.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
مرکز تقارن و محور تقارن
مرکز تقارن
وقتی شکلی به اندازه ی ۱۸۰ درجه (نیم دور) حول نقطه ای بچرخد و روی خودش منطبق شود، می گوییم شکل مرکز تقارن دارد با توجه به شکلهای زیر که در آنها هر شکل را ۱۸۰ درجه حول نقطه ی مشخص شده دوران داده ایم. نتیجه می شود که مربع مستطیل و متوازی الاضلاع دارای مرکز تقارن هستند، اما مثلث و ذوزنقه مرکز تقارن ندارند.
در متوازی الاضلاع مربع مستطیل و لوزی محل برخورد قطرها همان مرکز تقارن است.
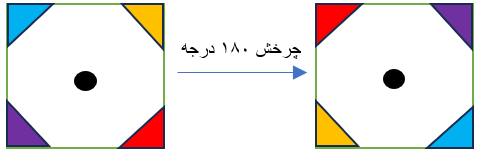
دقت داشته باشید اگر شکل زیر را ۱۸۰ درجه حول نقطه ی م بچرخانیم با توجه به این که رنگ های شکل اصلی جابه جا می شوند پس نقطه ی «م» نمی تواند مرکز تقارن شکل باشد.
چون رنگ های شکل های زیر برهم منطبق نمی شوند این شکل مرکز تقارن ندارد.
یادآوری محور تقارن
محور تقارن خطی است که شکل را به دو قسمت مساوی تقسیم می کند به طوری که اگر شکل را از روی آن خط تا کنیم، آن دو قسمت کاملاً بر هم منطبق شوند.
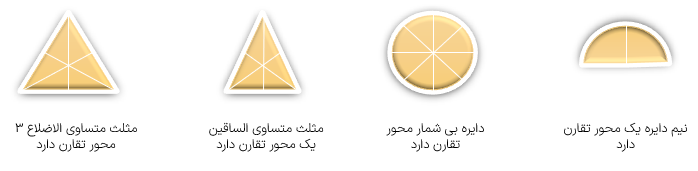
به خط تقارن هر شکل دقت کنید:
متوازی الاضلاع مثلث مختلف الاضلاع و تمامی ذوزنقه ها به غیر از ذوزنقه متساوی الساقین، محور تقارن ندارند.
دوران
دوران
در دوران (چرخش) غیر از ۱۸۰ درجه و ۳۶۰ درجه حتما باید جهت دوران مشخص شود که در جهت عقربه های ساعت است و یا در خلاف جهت عقربه های ساعت.
مثال
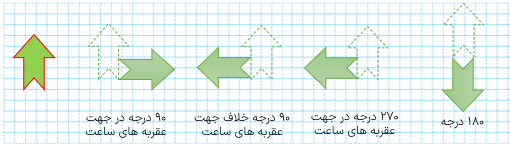
در صفحه ی شطرنجی ،زیر شکل «الف» را با دورانها مشخص شده ی زیر رسم کنید.
۱ ۹۰ درجه در جهت عقربه های ساعت
۲ ۹۰ درجه در جهت خلاف عقربه های ساعت
۳ ۲۷۰ درجه در جهت عقربه های ساعت
۴ ۱۸۰ درجه
1 دوران ۲۷۰ درجه در جهت عقربههای ،ساعت با دوران ۹۰ درجه در جهت خلاف عقربه های ساعت یکسان است.
2 اگر شکلی را حول یک نقطه به اندازه ی ۱۸۰ درجه یا کم تر بچرخانیم و شکل روی خودش قرار گیرد، می گوییم شکل دارای تقارن چرخشی است.
مثال
شکل مقابل تقارن چرخشی دارد، زیرا با دوران ۹۰ درجه حول نقطه ی «م» روی خودش قرار می گیرد.
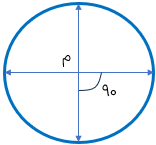
مثال
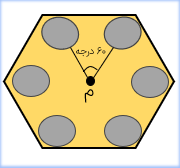
شکل مقابل نیز دارای تقارن چرخشی است زیرا با دوران ۶۰ درجه حول نقطه ی «م»، روی خودش قرار می گیرد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
تقارن چرخشی
تقارن چرخشی
وقتی شکلی را حول یک نقطه به اندازه ی ۱۸۰ درجه یا کم تر در جهت حرکت عقربه های ساعت بچرخانیم و شکل روی خودش منطبق شود میگوییم ،شکل تقارن چرخشی دارد به شکل های زیر دقت کنید.

چون این شکل بعد از ۹۰ درجه چرخش در جهت حرکت عقربه های ساعت دوباره روی خودش منطبق می شود، پس دوران چرخشی دارد.
چون این شکل بعد از ۱۸۰ درجه چرخش در جهت حرکت عقربههای ساعت دوباره روی خودش منطبق می شود پس دوران چرخشی دارد.
اگر شکل زیر را از ۱ تا ۱۸۰ درجه بچرخانیم هیچ گاه برخودش منطبق نمی شود لذا این شکل دوران چرخشی ندارد.
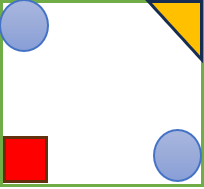
شکل زیر تقارن چرخشی دارد.
شکل زیر تقارن چرخشی ندارد.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
محورهای مختصات
محورهای مختصات
صفحهی مختصات از دو محور عمودی و افقی تشکیل شده است که به محور افقی، محور طول و به محور عمودی، محور عرض میگویند با توجه به تقسیم بندی روی این دو محور مکان هر نقطه روی صفحه را می توانیم تعیین کنیم که به آن مختصات نقطه می گویند.
مختصات نقطه را به صورت\(\left[ \begin{array}{l} \times \\ + \end{array} \right]\) نمایش می دهیم که عدد × را مؤلفه ی افقی (طول) نقطه و عدد + را مؤلفه ی عمودی (عرض) نقطه می گویند.
مؤلفه ی افقی در بالا و مؤلفه ی عمودی باید در پایین مختصات یک نقطه نوشته شود.
مثال
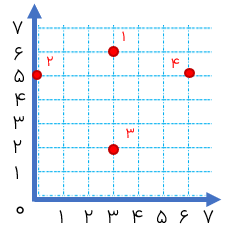
مختصات نقطه های زیر را با استفاده از صفحه ی مختصات مقابل بنویسید.
\(1 = \left[ \begin{array}{l}3\\6\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,2 = \left[ \begin{array}{l}0\\5\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3 = \left[ \begin{array}{l}3\\2\end{array} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4 = \left[ \begin{array}{l}6\\5\end{array} \right]\)
نقطه ی «م» که ابتدا مشترک دو محور ر است، دارای مختصات \(\left[ \begin{array}{l}0\\0\end{array} \right]\) است . و مختصات هر نقطه در صفحه مختصات، نسبت به این نقطه حساب می شود.
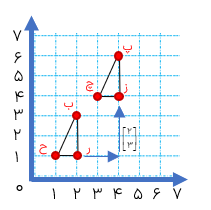
در صفحه ی مختصات مقابل، هر یک از رأس های مثلث (ب ر ح) را ۲ واحد به راست و ۳ واحد به بالا حرکت داده ایم تا مثلث(پ ز ج) به دست آید به این کار انتقال می گوییم.
ب=\(\left[ \begin{array}{l}2\\3\end{array} \right]\mathop \to \limits_{ + 3}^{ + 2} \left[ \begin{array}{l}4\\5\end{array} \right]\)
ح=\(\left[ \begin{array}{l}1\\1\end{array} \right]\mathop \to \limits_{ + 3}^{ + 2} \left[ \begin{array}{l}3\\4\end{array} \right]\)
ر=\(\left[ \begin{array}{l}2\\1\end{array} \right]\mathop \to \limits_{ + 3}^{ + 2} \left[ \begin{array}{l}4\\4\end{array} \right]\)
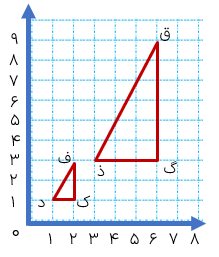
0صفحه ی ، مختصات زیر، مختصات سه رأس \( = \left[ \begin{array}{l}1\\1\end{array} \right]\) د , \( = \left[ \begin{array}{l}2\\1\end{array} \right]\) ک و \( = \left[ \begin{array}{l}2\\3\end{array} \right]\) ف از مثلث (د گ ف ) را سه برابر کرده ایم و به ترتیب رأس های از مثلث (ق ذ گ) به دست آمده است. چون مختصات سه برابر شده اند. پس محیط مثلث بدست امده سه برابر محیط مثلث اولی است و مساحت آن ۳ × ۳ یعنی ۹ برابر مساحت مثلث اول است.
ما معمولاً در زندگی روزمره از نقشه ها در پیدا کردن موقعیت ها و مکان هایی که شناخت کافی از آن ها نداریم، استفاده می کنیم هرنقطه روی نقشه با عددهایی مشخص میشود که در اصطلاح «مختصات» آن نقطه می گوییم.
مختصات نقطه
مختصات نقطه
مکان همه ی نقطه های موجود در یک صفحه را میتوانیم به کمک دو محور عمود برهم که در اصطلاح «محور مختصات» گفته می شود مشخص کنیم صفحه ی مختصات از دو محور عمود برهم که یکی از آن ها محور افقی (طول ها) و دیگری محور عمودی (عرض ها) میباشد تشکیل شده است. هر دو در نقطه ی صفر (مبدأ) مشترک هستند به دو عددی که با آن مکان نقطه را در صفحه تعیین میکنیم، مختصات آن نقطه می گوییم.
به صفحه مختصات زیر توجه کنید:
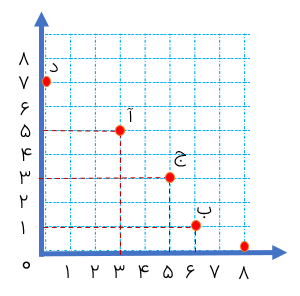
در صفحه ی مختصات زیر اگر از نقطه ی «آ» بر محورهای طول و عرض عمود کنیم، به این ترتیب طول نقطه ی «آ» برابر ۳ و عرض آن برابر ۵ می باشد. لذا نختصات این نقطه را به صورت \( = \left[ \begin{array}{l}3\\5\end{array} \right]\) آ می نویسیم و می خوانیم نقطه ی «آ» به طول3 و عرض ۵ همچنین مختصات نقاط دیگر هم برابر است با:
ج=\(\left[ \begin{array}{l}5\\3\end{array} \right]\)
ب=\(\left[ \begin{array}{l}6\\1\end{array} \right]\)
د=\(\left[ \begin{array}{l}0\\7\end{array} \right]\)
ه=\(\left[ \begin{array}{l}8\\0\end{array} \right]\)
همان طور که ملاحظه مي کنید، با توجه به نقاط آ و ج ، با جابه جا شدن طول و عرض هر نقطه جای نقطه در صفحه و در نتیجه مختصات آن تغییر می کند.
نقطه ی ه روی محور افقی یا همان محور طول ها قرار دارد. از طرفی عرض این نقطه برابر صفر است، پس هر نقطه که روی محور طول ها قرار داشته باشد، عرضش صفر است.
نقطه ی د روی محور عمودی یا همان محور عرض ها قرار دارد از طرفی طول این نقطه برابر صفر است پس هر نقطه که روی محور عرض ها قرار داشته باشد، طولش صفر است.
تعیین مختصات نقاط
برای تعیین مختصات هر نقطه توانیم از مبدأ مختصات شروع به حرکت افقی و سپس حرکت عمودی می کنیم تا به نقطه ی مورد نظر برسیم. سپس در قسمت بالای مختصات باید مقدار حرکت در جهت افقی و در قسمت پایین آن هم مقدار حرکت در جهت عمودی را بنویسیم.
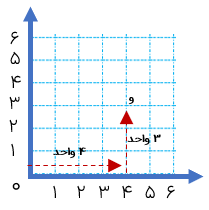
در صفحه ی مختصات مقابل اگر از مبدأ ۴ واحد به سمت راست و سپس واحد به سمت بالا حرکت کنیم به نقطه ی «و» می رسیم. پس:
مختصات نقطه ی «و» برابر\(\left[ \begin{array}{l}4\\3\end{array} \right]\) می باشد.
نمایش نقطه در صفحه ی مختصات
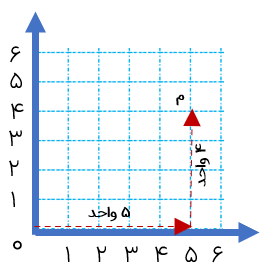
برای نمایش نقطه ای که مختصات آن معلوم است کافی است که از مبدأ مختصات ابتدا به اندازه ی عدد داده شده برای طول به صورت افقی و پس از آن به اندازه ی عدد داده شده برای عرض، به صورت عمودی حرکت کنیم تا به نقطه ی مورد نظر برسیم.
برای نمایش نقطه ی (\(\left[ \begin{array}{l}5\\4\end{array} \right]\) م) کافی است که از مبدأ ابتدا به اندازه ی ۵ واحد به صورت افقی و به سمت راست و پس از آن به اندازه ی ۴ واحد به صورت عمودی و به سمت بالا حرکت کنیم تا به نقطه ی «م» برسیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
رسم شکل های هندسی در صفحه مختصات
رسم شکل های هندسی در صفحه مختصات
اگر مختصات رأس های یک شکل هندسی معلوم ،باشد میتوانیم این رأس ها را در صفحه ی مختصات به طور دقیق مشخص نماییم، سپس آن نقاط را به وسیله ی خط کش به یک دیگر وصل می کنیم تا شکل مورد نظر رسم شود. حالا با شمردن تعداد مربع های داخل شکل یا استفاده از فرمول های محاسبه ی مساحت، می توانیم مساحت شکل مورد نظر را تعیین کنیم.
مثال
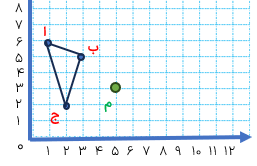
نقاط \( = \left[ \begin{array}{l}2\\1\end{array} \right]\) آ \( = \left[ \begin{array}{l}5\\1\end{array} \right]\) ب \( = \left[ \begin{array}{l}5\\4\end{array} \right]\) ج رأس های یک مثلث هستند. ابتدا مثلث را رسم کرده، سپس مساحت آن را حساب کنید.
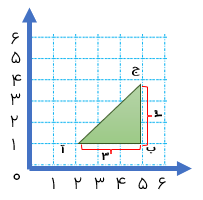
ابتدا نقاط بالا را به طور دقیق روی صفحه ی مختصات مشخص و آنها را به یک دیگر وصل میکنیم تا مثلث آب ج» به دست آید. همان طور که ملاحظه میکنید این مثلث قائم الزاویه است، پس مساحت آن برابر است با
۴/۵ = ۲ ÷ (۳×۳) = ۲ ÷ (قاعده × ارتفاع) = مساحت مثلث
بزرگ نمایی شکل ها در صفحه مختصات
به مختصات رأس های دو مستطیل «آ ب ج د» و «ا ز و ه» دقت کنید.
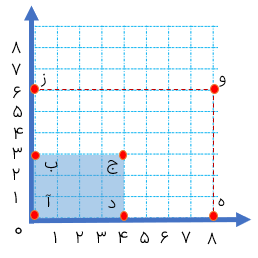
مستطیل «آ ز و ه» :
آ=\(\left[ \begin{array}{l}0\\0\end{array} \right]\) ب=\(\left[ \begin{array}{l}0\\3\end{array} \right]\) ج=\(\left[ \begin{array}{l}4\\3\end{array} \right]\) د=\(\left[ \begin{array}{l}4\\0\end{array} \right]\) آ=\(\left[ \begin{array}{l}0\\0\end{array} \right]\) ز=\(\left[ \begin{array}{l}0\\6\end{array} \right]\)
همان طور که ملاحظه کنید، ابعاد مستطیل بزرگ تر دو برابر ابعاد مستطیل کوچک تر است، اما مساحت آن ۴ برابر مساحت مستطیل کوچک تر می باشد.
۴۸ = ۶ × ۸ = مساحت مستطیل بزرگ
۱۲ = ۳ × ۴ = مساحت مستطیل کوچک تر
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
انتقال شکل در صفحه ی مختصات
انتقال شکل در صفحه ی مختصات
اگر در صفحه ی مختصات نقطه ای را جابه جا کنیم یک انتقال انجام داده ایم. به طور مثال اگر از نقطه ای مانند \(\left[ \begin{array}{l}1\\5\end{array} \right]\) = آ سه واحد به سمت راست و سپس دو واحد به سمت پایین حرکت کنیم به نقطه ی \(\left[ \begin{array}{l}4\\3\end{array} \right]\) = ب می رسیم به این ترتیب می گوییم که نقطه ی «آ» را به نقطه «ب» منتقل کرده ایم.
برای انتقال یک شکل در صفحه ی مختصات کافی است که ابتدا تمامی رأسها را به اندازه ی خواسته شده انتقال دهیم سپس نقاط به دست آمده را مانند شکل اولیه به یک دیگر وصل کنیم. به این ترتیب شکلی به دست می آید که با شکل اولیه مساوی است ولی در صفحه جابه جا شده است.
تقارن و مختصات
تقارن و مختصات
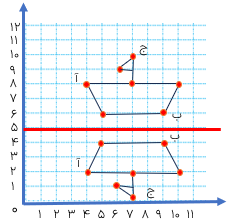
مثال قرینه ی نقطه\(\left[ \begin{array}{l}2\\7\end{array} \right]\) = ب نسبت به خط تقارن قرمز، نقطه ی \(\left[ \begin{array}{l}6\\7\end{array} \right]\) =ث است و قرینه ی نقطه ی «ب» نسبت به خط تقارن آبی، نقطه ی \(\left[ \begin{array}{l}2\\1\end{array} \right]\) = پ است.
دو نقطه ی «ب» و «ت» دارای مؤلفه های عمودی برابرند.
دو نقطه ی «ب» و «پ» دارای مؤلفه های افقی برابرند.
مؤلفه ی عمودی (عرض) هر نقطه و قرینه اش نسبت به یک خط عمودی با هم برابرند. مؤلفه ی افقی (طول) هر نقطه و قرینه اش نسبت به یک خط افقی با هم برابرند.
قرینه ی یک نقطه نسبت به خط تقارن عمودی
می دانیم که برای مشخص کردن قرینه ی یک نقطه نسبت به یک خط تقارن کافی است که از آن نقطه بر خط تقارن عمود کنیم و در طرف دیگر خط به همان اندازه پیش برویم در شکل مقابل نقطه ج=\(\left[ \begin{array}{l}6\\4\end{array} \right]\) قرینه ی نقطه ی ى آ=\(\left[ \begin{array}{l}2\\4\end{array} \right]\) نسبت به خط تقارن (ه و ) است همان طور که ملاحظه می کنید، عرض این دو نقطه با هم برابر است و خط تقارن دقیقا از نقاطی به طول ۴ (میانگین ۲ و ۶) عبور می کند.
قرینه ی یک نقطه نسبت به خط تقارن افقی
در محور مختصات زیر شکل۲(شکل پایین) قرینه ی شکل ۱ (شکل بالا) نسبت به خط تقارن افقی است.
همان طور که ملاحظه می کنید طول هر نقطه و قرینه ی آن نسبت به خط تقارن با هم برابر است.
آ= \(\left[ \begin{array}{l}4\\8\end{array} \right]\) و قرینه آ برابر=\(\left[ \begin{array}{l}4\\2\end{array} \right]\)
ب= \(\left[ \begin{array}{l}9\\6\end{array} \right]\) و قرینه ب برابر=\(\left[ \begin{array}{l}9\\4\end{array} \right]\)
ج= \(\left[ \begin{array}{l}7\\10\end{array} \right]\) و قرینه ج برابر=\(\left[ \begin{array}{l}7\\0\end{array} \right]\)
در دو نقطه که نسبت به یک خط تقارن افقی قرینه هستند طول ها ،برابر ولی عرضها متفاوت هستند.
قرینه ی یک نقطه نسبت به یک نقطه در صفحه مختصات
برای پیدا کردن قرینه ی یک نقطه نسبت به نقطه ی دیگر در صفحه ی مختصات می توانیم از روش های زیر استفاده کنیم
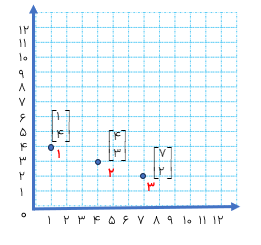
۱- جابه جایی:
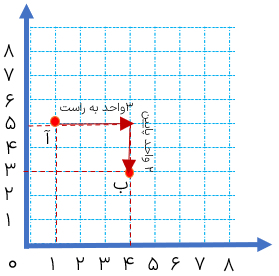
برای جابه جا شدن از نقطه ی \(1 = \left[ \begin{array}{l}1\\4\end{array} \right]\) به نقطه ی \(2 = \left[ \begin{array}{l}4\\3\end{array} \right]\) ، ابتدا باید به صورت افقی و به سمت راست ۳ واحد سپس به صورت عمودی و به سمت پایین یک واحد حرکت کنیم. حالا برای پیدا کردن قرینه ی «1»نسبت به نقطه ی «2» همین عمل را انجام می دهیم، یعنی از نقطه ی «2»ابتدا ۳ واحد افقی به سمت راست و سپس یک واحد عمودی به سمت پایین حرکت می کنیم تا به نقطه ی \(3 = \left[ \begin{array}{l}7\\2\end{array} \right]\) برسیم.
2- تقارن مرکزی:
از نقطه ی «1» به نقطه ی «2» وصل می کنیم و به همان اندازه در طرف دیگر نقطه ی «2» پیش می رویم: تا به نقطه ی «3» برسیم.
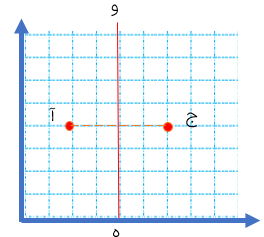
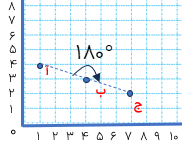
3- دوران ۱۸۰ درجه:
اگر نقطه ی «آ» را به اندازه ی ۱۸۰ درجه نسبت به نقطه ی م دوران دهیم (بچرخانیم)، به نقطه ی «ج» می رسیم.
برای رسم قرینه ی یک شکل نسبت به یک نقطه ابتدا باید قرینه ی تمامی رأس های شکل را با استفاده از یکی از روش های بالا (روش تقارن مرکزی ساده تر است) نسبت به نقطه ی داده شده مشخص کنیم. سپس نقاط مشخص شده را مانند شکل اصلی به یک دیگر وصل کنیم
مثال
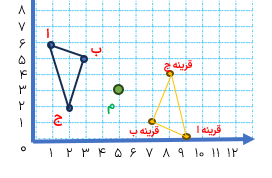
قرینه ی مثلث مقابل را نسبت به مرکز تقارن «م» رسم کنید سپس مختصات رأس های قرینه ی آن را بنویسید.
روش اول ابتدا با استفاده از تقارن ،مرکزی قرینه ی هر یک از نقاط «آ»، «ب» و «ج» را نسبت به نقطه ی «م» مشخص میکنیم سپس مختصات آن ها را می نویسیم.
ا=\(\left[ \begin{array}{l}1\\6\end{array} \right]\) و قرینه ا=\(\left[ \begin{array}{l}9\\0\end{array} \right]\)
ب=\(\left[ \begin{array}{l}3\\5\end{array} \right]\) و قرینه ب=\(\left[ \begin{array}{l}7\\1\end{array} \right]\)
ج=\(\left[ \begin{array}{l}2\\2\end{array} \right]\) و قرینه ج=\(\left[ \begin{array}{l}8\\4\end{array} \right]\)
حالا نقاط به دست آمده را در محور مختصات مشخص، و مثل شکل اصلی به یک دیگر وصل می کنیم تا شکل مانند شکل روش قبل شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم



1736019749.png)