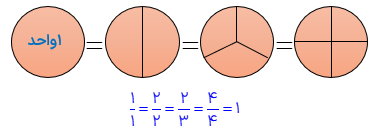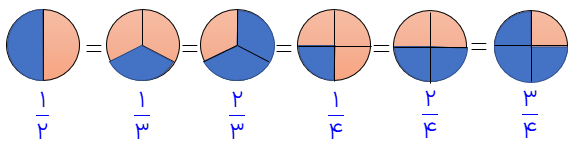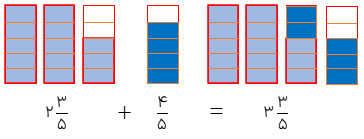درسنامه کامل ریاضی پنجم فصل 2 کسر
تعداد بازدید : 7.58Mخلاصه نکات ریاضی پنجم فصل 2 کسر - درسنامه شب امتحان ریاضی پنجم فصل 2 کسر - جزوه شب امتحان ریاضی پنجم نوبت اول فصل 2 کسر
مفهوم کسرها
مفهوم کسرها
وقتی یک شکل واحد را به قسمت های مساوی تقسیم کنیم و تعدادی از این قسمت ها را رنگ کنیم قسمت رنگ شده کسری از واحد را نشان می دهد. در نمایش ،کسرها مخرج کسر نشان دهنده تعداد كل قسمتهای مساوی شکل واحد میباشد و صورت کسر نیز نشان دهنده تعداد قسمت های رنگ شده می باشد.
مثال
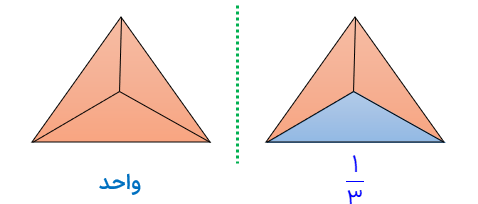
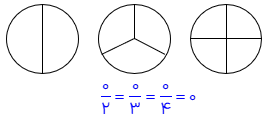
در مثال زیر شکل واحد یک مثلث است که به 3 قسمت مساوی تقسیم شده است. لذا مخرج کسر 3 می باشد ، تعداد خانه های رنگ ،شده یعنی صورت کسر نیز 1 می باشد.
مثال
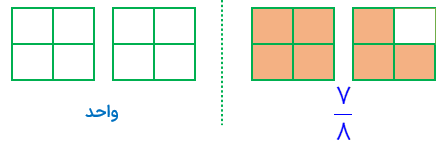
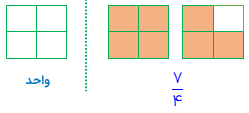
در مثال زیر دو تا مربع یک واحد را تشکیل می دهند که در سمت چپ خط چنین نشان داده شده است.
چون كل واحد (دو مربع) جمعا 8 قسمت مساوی ،دارند لذا مخرج کسر 8 می باشد. تعداد قسمت رنگی 7 قسمت است، لذا صورت کسر 7 می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
دسته بندی کسرها
دسته بندی کسرها
کسرها به دسته های زیر تقسیم میشوند:
الف) كسرهای برابر واحد:
کسری است که صورت و مخرج آن برابر واحد است. یعنی تمام قسمت های یک واحد کامل رنگ شده اند لذا یک واحد کامل بوده و برابر با 1 می باشد.
به این نکته توجه کنید که ما نمی توانیم شکلی رسم کنیم که آن را به صفر قسمت تقسیم کنیم تا عدد صفر در مخرج کسر قرار گیرد. لذا هیچگاه مخرج یک کسر صفر نخواهد بود.
ب) کسر کوچکتر از واحد:
در این نوع ،کسرها صورت از مخرج کوچکتر است. یعنی تعداد قسمت های رنگ شده از تعداد کل قسمت های شکل واحد کمتر است.
ج) کسر بزرگتر از واحد
کسر بزرگتر از ،واحد کسری است که صورت کسر از مخرج آن بزرگتر باشد برای رسم شکل مربوط به کسر بزرگتر از واحد یک یا چند شکل واحد کامل به همراه یک کسر کوچکتر از واحد رسم میشود. مثال زیر نمونه ای از کسر کوچکتر از واحد هستند.
د) کسر مساوی صفر
کسری که فقط صورت آن صفر باشد کسری مساوی صفر است. در رسم این نوع ،کسرها هیچ یک از قسمتهای کسر رنگ نمیشود و کل شکل بی رنگ باقی می ماند. زیرا تعداد واحدهای رنگ آمیزی صورت کسر صفر تعیین شده است.
مقدار رنگ شده در تمام شکل ها صفر است
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
نمایش کسر روی محور
نمایش کسر روی محور
برای نمایش کسر بر روی محور ابتدا می بایست هر واحد روی محور را به تعداد عدد مخرج كسر تقسیم کنیم سپس به تعداد صورت کسر از این واحدها شمارش میکنیم و از صفر محور به این نقطه وصل میکنیم
مثال
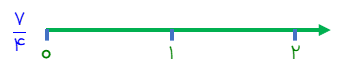
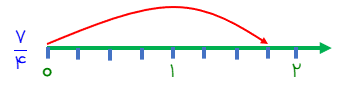
کسر زیر را روی محور نشان دهید.
مخرج كسر عدد 4 است پس باید بین واحدها را به چهار قسمت تقسیم .کنیم بعد به تعداد عدد صورت یعنی هفت شمارش کرده و از نقطه صفر به آن رسم میکنیم.
عدد مخلوط
عدد مخلوط
عدد مخلوط روش دیگری برای نمایش کسرهای بزرگتر از واحد است.
وقتی کسری بزرگتر از واحد بود باید تا آنجا که ممکن است واحدهای کامل را از آن بیرون بکشیم و به صورت عدد صحیح در کنار آنچه باقی مانده و کسر کوچکتر از واحد است قرار دهیم در این صورت عدد مخلوط را به دست آورده ایم. برای این کار باید صورت کسر را به مخرج تقسیم کنیم. بعد خارج قسمت تقسیم را به عنوان عدد صحیح در نظر میگیریم و باقیمانده تقسیم را به عنوان صورت بخش کسری نوشته و مقسوم عليه تقسيم را نیز به عنوان مخرج بخش کسری می نویسیم .
مثال
کسر زیر را با تقسیم کردن به عدد مخلوط تبدیل کنید. سپس با رسم شکل و محور آن را نمایش دهید.
\(\frac{{23}}{7}\)
\(\frac{{23}}{7} \Rightarrow 3\frac{2}{7}\)
تبدیل عدد مخلوط به کسر بزرگتر از واحد
برای تبدیل یک عدد مخلوط به کسر بزرگتر از واحد می بایست قسمت صحیح عدد سمت چپ کسر را در مخرج ضرب کرده و جواب هر چه به دست آمد با صورت کسر جمع کنیم و به عنوان صورت کسر جدید قرار میدهیم. مخرج کسر نیز بدون تغییر باقی می ماند.
مثال
عدد مخلوط زیر را به کسر تبدیل کنید
\(6\frac{2}{7}\)
\(\begin{array}{l}6\frac{2}{7} = \frac{{44}}{7}\\\\(7 \times 6 + 2 = 44)\end{array}\)
در اعداد مخلوط بين عدد صحیح و قسمت کسری علامتی قرار ندارد ولی در واقعیت بین آنها علامت جمع وجود دارد ولی نوشته نمی شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
مقایسه عدد مخلوط
مقایسه عدد مخلوط
برای مقایسه دو عدد ،مخلوط از روشهای زیر استفاده میکنیم.
الف) قسمت های صحیح دو عدد را با هم مقایسه می کنیم:
هر کدام عدد صحیح بزرگتری داشت آن عدد مخلوط، بزرگتر است.
عدد مخلوط باید استاندارد باشد یعنی کسری عدد مخلوط باید خودش کوچکتر از واحد باشد و در غیر اینصورت می بایست قسمت کسری خوبه عدد مخلوط دیگری تبدیل شده و با عدد صحیح اولیه جمع شود آنگاه مقایسه صورت پذیرد.
مثال
دو عدد مخلوط زیر را مقایسه کنید.( به نکته بالا دقت کنید)
\(3\frac{4}{5}\left\lfloor {} \right\rfloor 2\frac{7}{2}\)
\(\begin{array}{l}3\frac{4}{5}\left\lfloor < \right\rfloor 2\frac{7}{2}\\\\\frac{7}{2} = 3\frac{1}{2}\\\\3\frac{4}{5}\left\lfloor < \right\rfloor 2 + 3\frac{7}{2}\end{array}\)
بخش کسری بزرگتر از واحد است. باید خودش به عدد مخلوط تبدیل شود.
ب) مقایسه دو عدد مخلوط دارای اعداد صحیح برابر:
هر گاه در مقایسه دو عدد مخلوط قسمت عدد صحیح هر دو با همدیگر برابر بود، سراغ قسمت کسری رفته و آنها را مقایسه میکنیم و هر کدام قسمت کسری بزرگتری ،داشت آن عدد مخلوط بزرگتر است. در مقایسه کسرها یکی از حالات زیر مشاهده میشود:
حالت اول:
در اعداد مخلوط با عدد صحیح برابر اگر مخرج دو کسر برابر ،باشد کسری بزرگتر است که صورت بزرگتری داشته باشد.
مثال
\(\begin{array}{l}\,\,\,\,\,\,\,2 < 4\\\\3\frac{2}{5}\,\,\left\lfloor < \right\rfloor \,\,3\frac{4}{5}\end{array}\)
حالت دوم:
در اعداد مخلوط با عدد صحیح برابر اگر صورت دو کسر برابر ،باشد کسری بزرگتر است که مخرج کوچکتری داشته باشد.
مثال
\(\begin{array}{l}3\frac{4}{7}\left\lfloor < \right\rfloor 3\frac{4}{5}\\\\\,\,\,\,\,\,\,\,7 > 5\end{array}\)
حالت سوم :
در اعداد مخلوط با عدد صحیح برابر اگر مخرج دو کسر برابر باشد و صورت دو کسر نیز برابر باشد آن دو کسر با هم برابرند.
مثال
\(3\frac{4}{5}\left\lfloor = \right\rfloor 3\frac{4}{5}\)
حالت چهارم :
در اعداد مخلوط با عدد صحیح برابر اگر مخرج دو کسر برابر نباشد و صورت نیز برابر نباشد با نوشتن کسرهای مساوی با هر کدام صورت ها یا مخرج ها را برابر کرده و سپس با یکی از 3 حالت بالا آنها را با هم مقایسه می کنیم.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
جمع و تفریق عددهای مخلوط
جمع و تفریق عددهای مخلوط
در جمع و تفریق اعداد مهمترین کار یکسان نمودن مخرج کسرها می باشد. در زیر نمونه هایی از روشهای جمع و تفریق اعداد مخلوط را مشاهده میکنید
استفاده از شکل
برای جمع دو عدد مخلوط به روش رسم شکل ابتدا اگر مخرج یکسان ، نداشتند، آنها را هم مخرج کرده و بعد شکل مربوطه را رسم کرده و عملیات جمع یا تفریق را انجام میدهیم.
در جمع برای هر کسر یک شکل رسم میکنیم و بعد شکلها را کنار هم گذاشته و جمع می کنیم. دقت کنید گاهی از جمع دوتا ،کسر کسری بزرگتر از واحد درست میشه که میتوان واحد کامل را از داخل آن بیرون کشید و با عدد صحیح جمع
کرد. در تفریق کسر مربوط به عدد مخلوط اول را رسم کرده و به اندازه کسر یا عدد مخلوط دوم از آن خط می زنیم اگر بخش کسری کسر دوم کوچکتر از بخش کسری کسر اول بود میبایست از بخش عدد صحیح کسر اول نیز خط بزنیم
مثال
\(2\frac{2}{3} + \frac{5}{6} \Rightarrow 2\frac{4}{6} + \frac{5}{6}\)
با رسم محور
در این روش ابتدا کسرها را هم مخرج می کنیم بعد اندازه بین واحدها را به اندازه مخرج به قسمت های مساوی تقسیم میکنیم.
عدد مخلوط اول را با فلشی که شروع آن از صفر میباشد روی محور نمایش میدهیم و عدد مخلوط دوم را از انتهای فلش دوم رسم میکنیم اگر جمع بود به سمت راست و اگر تفریق بود به سمت چپ رسم میکنیم جهت راحتی کار میتوان عدد مخلوط دوم را به کسر بزرگتر از واحد تبدیل کرد و بعد فلش آن را رسم کرد.
مثال
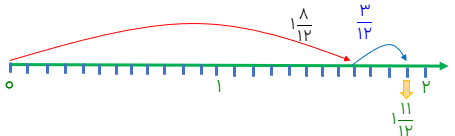
\(1\frac{2}{3} + \frac{1}{4} \Rightarrow 1\frac{8}{{12}} + \frac{3}{{12}}\)
محاسبه ریاضی
ابتدا اعداد صحیح را با هم جمع میکنیم و بعد کسرها را اگر مخرج برابر نداشتند، هم مخرج نموده و با هم جمع میکنیم. در انتها اگر بخش کسری جواب بزرگتر از واحد بود، آن را به عدد مخلوط تبدیل کرده و با عدد صحيح جمع میکنیم.
مثال
جمع دو عدد مخلوط زیر ،را با روش محاسبه ریاضی به دست آورید.
\(1\frac{2}{3} + 2\frac{1}{4}\)
\(1\frac{2}{3} + 2\frac{1}{4} \Rightarrow 1\frac{8}{{12}} + 2\frac{3}{{12}} = 3\frac{{11}}{{12}}\)
انجام عملیات تفریق
ابتدا كسرها را اگر دارای مخرج برابر نیستند هم مخرج می.کنیم بعد مقایسه می کنیم آیا بخش کسری عدد مخلوط اول از بخش کسری عدد مخلوط دوم بزرگتر هست که قابل تفریق باشد یا خیر؟
اگر بخش کسری عدد مخلوط اول از بخش کسری عدد مخلوط دوم بزرگتر بود اعداد صحیح دوم را از عدد صحیح اولی کم میکنیم و بعد کسر دوم را نیز از کسر اول کم میکنیم.
مثال
تفریق عدد مخلوط زیر را انجام دهید.
\(4\frac{3}{4} - 1\frac{2}{3}\)
\(4\frac{3}{4} - 1\frac{2}{3} = 4\frac{9}{{12}} - 1\frac{8}{{12}} = 3\frac{1}{{12}}\)
اگر در جمع یا تفریق اعداد مخلوط یکی از اعداد نداشت و تنها دارای قسمت کسری صحيح بود به این معنی است که عدد صحیح آن صفر می باشد.
اگر در تفریق اعداد مخلوط قسمت کسری عدد مخلوط اولی از قسمت کسری عدد مخلوط دوم کوچکتر باشد امکان تفریق عدد بزرگ از یک عدد کوچک وجود ندارد بنابراین به کمک قسمت عدد صحیح عدد مخلوط نیز نیاز داریم لذا به یکی از دو روش زیر اقدام میکنیم:
روش اول:
در روش اول هر دو عدد مخلوط را به کسر بزرگتر از واحد تبدیل میکنیم تا عدد صحیح به کمک بخش کسری آمده و کسر اول به کمک یک واحد عدد صحیح بزرگتر شده و امکان تفریق وجود داشته باشد و سپس تفریق را انجام می دهیم. در نهایت اگر جواب تفریق کسر بزرگتر از واحد ه بود آن را مجددا به عدد مخلوط تبدیل میکنیم
مثال
تفریق دو عدد مخلوط زیر را به دست آورید.
\(4\frac{1}{3} - 2\frac{2}{3}\)
\(4\frac{1}{3} - 2\frac{2}{3} = \frac{{13}}{3} - \frac{8}{3} = \frac{5}{3} = 1\frac{2}{3}\)
روش دوم:
در روش دوم یک واحد از عدد صحیح مربوط به عدد مخلوط اول کم کرده و به کسر آن اضافه میکنیم حالا قسمت کسری آن به کمک این یک واحد بزرگتر شده و امکان تفريق وجود دارد، لذا عملیات تفریق را انجام میدهیم.
مثال
تفریق دو عدد مخلوط زیر را به دست آورید.
\(4\frac{1}{3} - 2\frac{2}{3}\)
کسر اول از کسر دوم کوچکتر است و تفریق نمی شود.
\(\begin{array}{l}4\frac{1}{3} - 2\frac{2}{3} = 3 + 1\frac{1}{3} - 2\frac{2}{3}\\ = 3 + \frac{4}{3} - 2\frac{2}{3}\\ = 3\frac{4}{3} - 2\frac{2}{3}\\ = (3 - 2) + (\frac{4}{3} - \frac{2}{3})\\ = 1 + \frac{2}{3}\end{array}\)
ضرب عدد در کسر
ضرب عدد در کسر
برای به دست آوردن حاصل ضرب یک عدد در یک کسر سه روش زیر وجود دارد:
استفاده از شکل
در این روش ابتدا باید شکل واحد را انتخاب کنیم تا بدانید یک واحد کامل به چند قسمت تقسیم شده .است زیرا شکل به هر چند قسمت مساوی که تقسیم شود این تعداد قسمتها نشان دهنده مخرج کسر است.
بعد از اینکه شکل واحد و تعداد قسمتها مشخص شد به تعداد عدد داده شده که قرار است در کسر ضرب ،شود با رنگهای مختلف کسر مورد نظر را نشان می دهیم.
مثال
حاصل ضرب زیر را با رسم شکل به دست آورید.
\(2 \times \frac{1}{3}\)
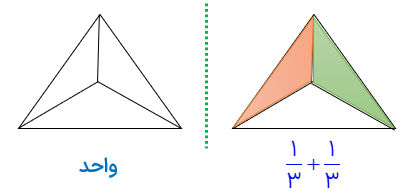
با توجه به شکل ،واحد مخرج کسر 3 بوده و تا انتهای محاسبات تغییر نمی کند صورت کسر 1 است و عددی که ضرب شده 2 است. پس 2 نوع رنگ لازم داریم که از هر رنگ تعداد 1 خانه باید رنگ شود. (اگر لازم بود می توانستم تعداد مثلث ها را بیشتر کنیم تا بتوانیم به تعداد مورد نیاز خانه رنگ کنیم).
واحد به ۳ قسمت مساوی تقسیم شده، پس مخرج ۳ می باشد.
\(\frac{1}{3} + \frac{1}{3} = 2 \times \frac{1}{3} = \frac{2}{3}\)
با رسم محور:
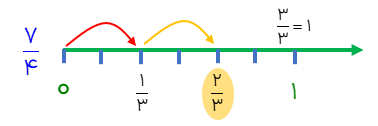
در این روش ابتدا به اندازه کسر داده شده از صفر محور یک فلش می کشیم و بعد این فلش را تعداد عددی که در کسر ضرب شده است تکرار می کنیم
مثال
حاصل ضرب زیر را با رسم محور به دست آورید .
\(2 \times \frac{1}{3}\)
\(2 \times \frac{1}{3} = \frac{2}{3}\)
محاسبه ریاضی:
در این روش عدد ضرب شده در کسر را فقط در صورت کسر ضرب میکنیم و مخرج بدون تغییر ماند. باقی می ماند.
مثال
حاصل ضرب زیر را با محاسبه ریاضی به دست آورید.
\(7 \times \frac{3}{4}\)
عدد 7 فقط در صورت کسر یعنی 3 ضرب می شود و مخرج کسر بدون تغییر باقی می ماند.
\(7 \times \frac{3}{4} = \frac{{7 \times 3}}{4} = \frac{{21}}{4}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
ضرب کسر در کسر
ضرب کسر در کسر
برای به دست آوردن حاصل ضرب دو ،کسر یکی از سه روش زیر را به کار می بریم.
استفاده از شکل:
در این روش طبق مراحل زیر اقدام میکنیم شکل واحد را انتخاب می کنیم:
1 شكل واحد را انتخاب می کنیم.
2 شكل واحد را به تعداد مخرج کسر دوم تقسیم بندی می کنیم .
3 به اندازه صورت کسر ،دوم، از قسمتهای شکل رنگ می کنیم.
4 حالا سراغ کسر دوم می رویم.
5 قسمت رنگ شده کسر را در نظر میگیریم و به قسمت رنگ نشده کار نداریم.
6 این قسمت رنگ شده کسر را به اندازه مخرج كسر اول جداگانه تقسیم بندی می کنیم.
7 حالا از این تقسیم بندی جدید که انجام داده ایم به اندازه صورت کسر اول با رنگی دیگر رنگ آمیزی می کنیم
8 حالا کسر جواب را می نویسیم که در آن قسمت رنگ شدهی ،جدید صورت کسر بوده وتعداد كل تقسیم بندی شکل چه رنگ شده و چه رنگ نشده مخرج کسر می باشد.
مثال
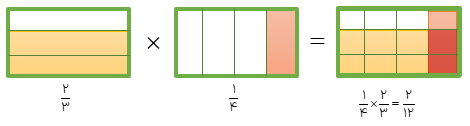
حاصل ضرب دو کسر زیر را با استفاده از رسم شكل به دست آورید.
\(\frac{1}{4} \times \frac{2}{3}\)
با رسم محور:
در این روش به اندازه کسر دوم از صفر محور یک فلش رسم می کنیم.
حالا قسمتی که جدا کرده ایم و با فلش نشان داده ایم را به اندازه مخرج کسر اول تقسیم بندی کرده و به اندازه صورت کسر اول از آن انتخاب می کنیم و بعد یک فلش دیگر (با شروع از نقطه صفر محور) رسم می کنیم.
محل فلش دوم جواب ضرب می باشد.
مثال
حاصل دو کسر زیر را با رسم نمودار به دست آورید.
\(\frac{1}{2} \times \frac{3}{5}\)
ابتدا کسر دوم را با فلش نمایش میدهیم و محدوده بالا را به اندازه مخرج کسر اول به دو قسمت تقسیم کرده و به اندازه صورت آن را انتخاب میکنیم
محل فلش دوم (زرد رنگ) جواب است
محاسبه ریاضی:
در ضرب دو کسر در ،همدیگر صورت کسر اول در صورت کسر دوم ضرب میشود و مخرج کسر اول نیز در مخرج کسر دوم ضرب می شود.
در ضرب کسرها اصلا نیازی به هم مخرج کردن کسرها نیست.
مثال
حاصل ضرب زیر را از طریق محاسبه ریاضی به دست آورید.
\(\frac{1}{2} \times \frac{3}{5}\)
\(\frac{1}{2} \times \frac{3}{5} = \frac{{1 \times 3}}{{2 \times 5}} = \frac{3}{{15}}\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
ضرب عددهای مخلوط
ضرب عددهای مخلوط
عددهای مخلوط را میتوان به دو روش در هم ضرب کرد:
استفاده از شکل:
در این ،روش برای ضرب دو عدد مخلوط مستطیلی رسم می کنیم و عدد کوچکتر را به عنوان عرض مستطیل و عدد بزرگ تر را به عنوان طول مستطیل در نظر می گیریم.
در مرحله بعد قسمت های صحیح و کسری اعداد مخلوط طول و عرض را با پاره خط جدا می کنیم با این کار مستطیل بزرگ به چند مستطیل کوچکتر تقسیم میشود و با به دست آوردن مساحت این مستطیلها و جمع آنها با همدیگر مساحت مستطیل بزرگتر و در نتیجه ضرب دو عدد مخلوط به دست می آید.
روش حل ضرب اعداد مخلوط با رسم شکل را می توانیم بدون اینکه خود شکل را رسم کنیم ولی از فرمول رسم استفاده کنیم نیز حل کنیم برای حل باید مراحل زیر را انجام دهیم
الف عدد صحیح مربوط به عدد مخلوط اول را در عدد صحیح مربوط به عدد مخلوط دوم ضرب می کنیم
ب عدد صحیح مربوط به عدد مخلوط اول را در کسر مربوط به عدد مخلوط دوم ضرب می کنیم.
ج عدد کسری مربوط به عدد مخلوط اول را در عدد صحیح مربوط به عدد مخلوط دوم ضرب می کنیم
د عدد کسری مربوط به عدد مخلوط اول را در کسر مربوط به عدد مخلوط دوم ضرب می کنیم
در مرحله آخر جوابهای "الف" ، "ب" ، "ج" ، "د" را با هم جمع می کنیم.
محاسبه ریاضی:
در این روش ابتدا هر دو عدد مخلوط را به کسر بزرگتر از واحد تبدیل کرده و سپس عددهای مخلوط را در هم ضرب می کنیم. در نهایت جواب را مجددا به عدد مخلوط تبدیل می کنیم
مثال
حاصل همان مثال قبلی را با روش محاسبه ریاضی به دست آورید
\(1\frac{1}{2} \times 2\frac{1}{3}\)
\(1\frac{1}{2} \times 2\frac{1}{3} = \frac{3}{2} \times \frac{7}{3} = \frac{{21}}{6} = 3\frac{3}{6} = 3\frac{1}{2}\)
ساده کردن در ضرب کسرها
ساده کردن در ضرب کسرها
در ضرب کسرها عملیات ساده کردن به دو روش قابل انجام است.
الف ابتدا کسرها را ساده کنیم و بعد عملیات ضرب را انجام دهیم .
ب عملیات ضرب کسرها را انجام دهیم و بعد جواب به دست آمده را ساده کنیم.
مثال
حاصل ضرب های زیر را به دست آورده و در آخر جواب را ساده کنید
\(\frac{7}{4} \times \frac{2}{5}\)
\(\frac{7}{4} \times \frac{2}{5} = \frac{{7 \times 2}}{{4 \times 5}} = \frac{{14 \div 2}}{{20 \div 2}} = \frac{7}{{10}}\)
اگر در صورت و مخرج کسر فقط از عملیات ضرب استفاده شده ،باشد میتوانیم اعداد صورت و مخرج را بر عددی مشترک تقسیم کنیم و عدد قبلی را خط بزنیم و حاصل تقسیم را به جای آن قرار دهیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
تقسیم کسرها
تقسیم عدد بر عدد
برای تقسیم دو عدد بر همدیگر میتوانیم از روش های زیر استفاده کنیم.
الف) استفاده از شکل:
در این روش اگر اگر عدد اول صورت کسر کوچکتر از عدد دوم مخرج کسر بود، شکل واحدی را در نظر گرفته و به اندازه مخرج به قسمت های مساوی تقسیم نموده و به اندازه صورت کسر از این قسمتها رنگ میکنیم.
مثال
تقسیم دو عدد زیر را با رسم شکل نشان دهید.
\(3 \div 5 = \frac{3}{5}\)
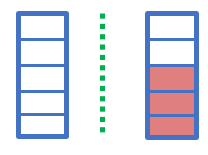
ولی اگر عدد اول صورت کسر بزرگتر از عدد دوم مخرج کسر بود آن را به عدد مخلوط تبدیل میکنیم و به تعداد عدد صحيح واحد کامل رسم میکنیم و به اندازه عدد کسری که کوچکتر از واحد است نیز شکلی مانند روشی که در بالا گفتیم رسم میکنیم.
ب)با رسم محور:
در این نوع نمایش روی محور اگر عدد اولی صورت کسر از عدد دوم مخرج کسر کوچکتر بود، یعنی کسر کوچکتر از واحد بود، بین سفر تا یک را به اندازه مخرج کسر به اندازه های مساوی تقسیم کرده و بعد به اندازه صورت از این قسمتها انتخاب میکنیم ولی اگر کسر بزرگتر از واحد بود باید ابتدا آن را به عدد مخلوط تبدیل کرده و بعد روی محور نمایش دهیم. که در این صورت باید به اندازه عدد صحیح از روی محور انتخاب کرده و فاصله بین عدد صحیح و عدد بعدی را اندازه مخرج کسر تقسیم بندی کرده و بعد به اندازه صورت از آن انتخاب کنیم.
ج)محاسبه ریاضی :
برای تقسیم دو عدد بر یکدیگر می بایست عدد اول را در صورت کسر نوشته و عدد دوم را در مخرج بنویسیم. اگر قابل ساده کردن بود ساده میکنیم و اگر بزرگتر از واحد بود به عدد مخلوط تبدیل می کنیم.
تقسیم کسر بر عدد
برای تقسیم کسر بر عدد به روشهای زیر عمل می کنیم.
الف) استفاده از شکل:
ابتدا شکل را به اندازه کسر اول رسم کرده و بعد دوباره همان شکل را به اندازه عدد مجددا تقسیم بندی میکنیم بخش رنگی مشخص شده در یکی از قسمتها جواب تقسیم است.
مثال
حاصل تقسیم کسر بر عدد زیر را با رسم شکل نشان دهید.
\(\frac{2}{5} \div 3\)

ب) با رسم محور :
در این روش ابتدا کسر را با فلش نمایش می دهیم. سپس قسمت مشخص شده با فلش را به تعداد عدد دوم به قسمتهای مساوی تقسیم می کنیم یکی از قسمتهای جدید جواب تقسیم می باشد.
ج)محاسبه ریاضی:
در این روش کسر اول را می نویسیم و بعد علامت تقسیم را به ضرب تقسیم کرده و به عدد دوم مخرج 1 میدهیم و جای صورت و مخرج را عوض می کنیم کسری می نویسیم که صورت آن 1 بوده و مخرجش این عدد میباشد حالا عمل ضرب را انجام میدهیم.
مثال
حاصل تقسیم کسر بر عدد زیر را با محاسبه ریاضی به دست آورید
\(\frac{1}{5} \div 3\)
\(\frac{1}{5} \div 3 = \frac{1}{5} \times \frac{1}{3} = \frac{1}{{15}}\)
تقسیم عدد بر کسر
الف) استفاده از شکل :
در این روش ابتدا به تعداد عدد داده شده، شکل واحد رسم میکنیم، بعد به اندازه مخرج کسر هر شکل را تقسیم بندی می کنیم تعداد قسمتهای بدست آمده در شکل جواب نهایی تقسیم می باشد.
مثال
حاصل تقسیم عدد بر کسر زیر را با استفاده از رسم شکل محاسبه کنید.
\(3 \div \frac{1}{5}\)
عدد ما ۳ است، پس ۳ واحد رسم میکنیم و مخرج کسر ۵ است پس هر واحد را به ۵ قسمت تقسیم میکنیم.
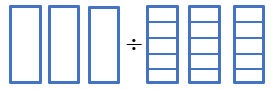
تعداد کل قسمت ها 15 شده است. جواب = 15
ب) با رسم محور :
در این روش به تعداد عدد داده شده باید روی محور واحد در نظر بگیریم و بعد این واحدها را به اندازه ی مخرج کسر تقسیم میکنیم تعداد قسمتهای کوچک به دست آمده جواب تقسیم می باشد.
مثال
حاصل تقسیم بر کسر زیر را با استفاده از رسم محور به دست آورید.
\(3 \div \frac{1}{5}\)
عدد ما ۳ است. روی محور ۳ واحد در نظر میگیریم.مخرج کسر ۵ است. هر واحد به ۵ قسمت تقسیم میشود
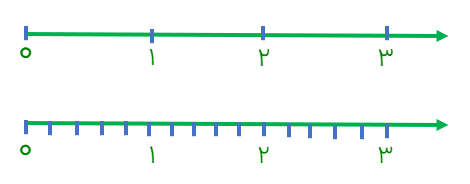
تعداد کل قسمتهای جدید ۱۵ تا میباشد = جواب15
ج) محاسبه ریاضی :
در این روش عدد را مینویسیم. بعد علامت تقسیم را به ضرب تبدیل می کنیم در انتها جای صورت و مخرج کسر را با هم عوض میکنیم و عمل ضرب را انجام میدهیم.
مثال
حاصل تقسیم عدد بر کسر زیر را با استفاده از محاسبه ریاضی به دست آورید.
\(3 \div \frac{1}{5}\)
\(3 \div \frac{1}{5} = 3 \times \frac{5}{1} = \frac{{15}}{1} = 15\)
نکات مهم زیر را به خاطر بسپارید
نیم یعنی:\(\frac{1}{2}\) ثلث یعنی:\(\frac{1}{3}\)
ربع یعنی:\(\frac{1}{4}\)
خمس یعنی:\(\frac{1}{5}\)



1736019749.png)