جواب تمرین صفحه 131 درس 6 ریاضی دهم (شمارش، بدون شمردن)
تعداد بازدید : 86.39Mپاسخ تمرین صفحه 131 ریاضی دهم
-گام به گام تمرین صفحه 131 درس شمارش، بدون شمردن
-تمرین صفحه 131 درس 6
-شما در حال مشاهده جواب تمرین صفحه 131 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در یک لیگ فوتبال 18 تیم قرار دارند. در پایان این لیگ تیم های اول تا سوم به چند حالت مختلف می توانند مشخص شوند؟

\(P\left( {18\:,\:3} \right) = \frac{{18!}}{{\left( {18 - 3} \right)!}} = \frac{{18!}}{{15!}} = 18\: \times \:17\: \times \:16 = 4896\)
2 از بین تعدادی کتاب مختلف می خواهیم سه کتاب را انتخاب کنیم و در قفسه ای بچینیم. اگر تعداد حالت های مختلف برای این کار 210 تا باشد، تعداد کتاب ها چند تاست؟
\(\begin{array}{*{20}{l}}{P\left( {n\:,\:3} \right) = \frac{{n!}}{{\left( {n - 3} \right)!}} = n\: \times \:\left( {n - 1} \right)\: \times \:\left( {n - 2} \right) = 210 \Rightarrow n = 7}\end{array}\)
3 کدام یک از موارد زیر درست و کدام نادرست است؟
6! = 3! + 3!
6! = 6 × 5!
8! = 4! × 2!
2 × 3! = 6!
(3!)2 = 9!
\(4!\; = \frac{{8!}}{{2!}}\)
6! = 3! + 3! نادرست:
6! = 6 × 5! درست:
8! = 4! × 2! نادرست:
2 × 3! = 6! نادرست:
(3!)2 = 9! نادرست:
\(4!\; = \frac{{8!}}{{2!}}\) نادرست
4 در یک نوع ماشین حساب کوچک که دارای 20 کلید است، برای انجام یک دستور خاص باید سه کلید مشخص با ترتیبی مشخص فشار داده شوند. اگر فردی نداند سه کلید مورد نظر کدام اند و بخواهد به طور تصادفی این کار را انجام دهد و فشردن هر سه کلید 2 ثانیه زمان بخواهد، این فرد حداکثر (در بدترین حالت) در چه زمانی می تواند دستور مورد نظر را اجرا کند؟
زمان مورد نیاز \( = 2\: \times \:P\left( {20\:,\:3} \right) = \)
\(\begin{array}{*{20}{l}}{2\: \times \:\frac{{20!}}{{\left( {20 - 3} \right)!}} = 2\: \times \:\frac{{20!}}{{17!}} = }\end{array}\)
\(2\: \times \:20\: \times \:19\: \times \:18 = 13680\) ثانیه
5 با حروف کلمهٔ «گل پیرا» و بدون تکرار حروف
الف چند کلمهٔ 6 حرفی می توان نوشت؟ چند تا از آنها با «گل» شروع می شود؟
ب چند کلمهٔ 4 حرفی می توان نوشت؟
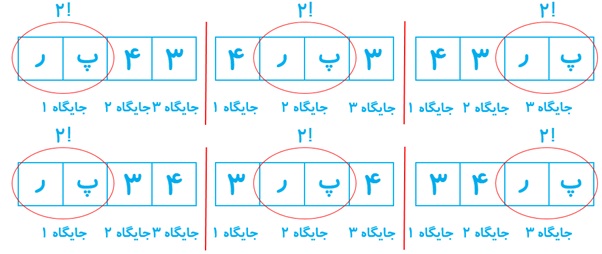
پ چند کلمهٔ ٦حرفی می توان نوشت که در آنها دو حرف «پ» و «ر» در کنار هم آمده باشند؟
ت چند کلمهٔ 4 حرفی می توان نوشت که در آنها دو حرف «پ» و «ر» در کنار هم آمده باشند؟
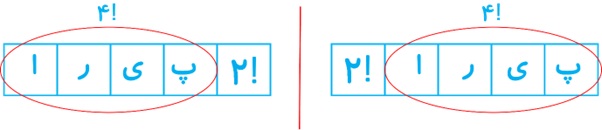
ث چند کلمهٔ 5 حرفی می توان نوشت که در آنها حروف کلمهٔ «پیرا» کنار هم آمده باشند؟
الف !6
هنگامی که 2 حرف از 6 حرف انتخاب شده است،پس 4 حرف باقی می ماند؛ بنابراین داریم: !4
ب \(\begin{array}{*{20}{l}}{P\left( {6\:,\:4} \right) = \frac{{6!}}{{\left( {6 - 4} \right)!}} = \frac{{6!}}{{2!}} = 6\: \times \:5 \times 4 \times 3 = 360}\end{array}\)
پ

ت
\(\begin{array}{l}2!\: \times \:P\left( {6 - 2\:,\:4 - 2} \right) \times 3!\\\\ = 2!\: \times \:P\left( {4\:,\:2} \right)\: \times 3!\\\\ = 2!\: \times \:\frac{{4!}}{{\left( {4 - 2} \right)!}}\: \times 3!\\\\ = 2!\: \times \:\frac{{4!}}{{2!}}\: \times 3! = 24\: \times \:6 = 144\end{array}\)
ث توضیح اینکه چون حرف های پ و ر می خواهند کنار هم باشند، پس 2 جایگشت برای آن ها داریم. در نتیجه دو جایگاه از 4 جایگاه اشغال می شود و از 6 حرف، 4 حرف باقی می ماند. همچنین در 2 جایگاه باقی مانده می تواند 2 حرف از 4 حرف باقی مانده قرار بگیرند، در نتیجه می شود (2 , 4)P . در آخر چون حروف کنار هم پ و ر را می توانیم یک واحد جداگانه فرض کنیم، پس فرض می کنیم که به جای 4 جایگاه، می خواهد 3 جایگاه توسط حروف اشغال شوند. در نتیجه تعداد قرار گیری جایگاه ها هم می شود !3. به عبارت دیگر:
\(\begin{array}{l}4!\, \times \,P\left( {6 - 4\,,\,5 - 4} \right) \times 2! = \\\\4!\, \times \,P\left( {2\,,\,1} \right)\, \times 2! = 4!\, \times \,\frac{{2!}}{{\left( {2 - 1} \right)!}}\, \times 2! = \\\\4!\, \times \,\frac{{2!}}{{1!}}\, \times 2! = 24\, \times \,2\, \times \,2 = 96\end{array}\)
ث توضیح آن مانند توضیح قسمت (ت) می باشد. به عبارت دیگر :
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















