جواب تمرین صفحه 105 درس 5 ریاضی دهم (تابع)
تعداد بازدید : 86.39Mپاسخ تمرین صفحه 105 ریاضی دهم
-گام به گام تمرین صفحه 105 درس تابع
-تمرین صفحه 105 درس 5
-شما در حال مشاهده جواب تمرین صفحه 105 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 کدام یک تابع است؟
دامنه و برد هر تابع را معلوم کنید.
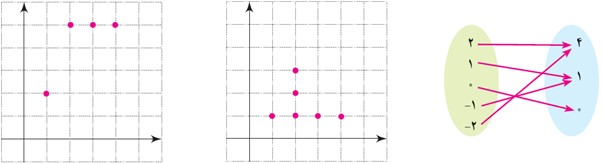
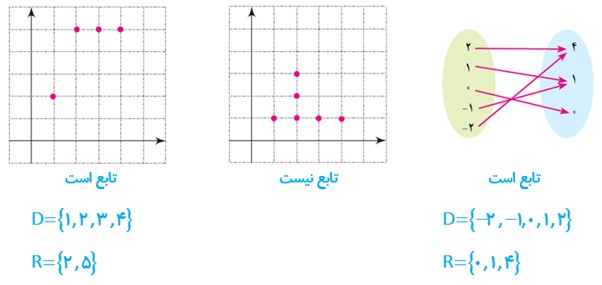
2 تابعی مثال بزنید که:
الف دامنهٔ آن تنها شامل دو عضو باشد.
ب برد آن تنها از یک عضو تشکیل شده باشد.
پ دامنهٔ آن تنها یک عضو داشته باشد.
ت دامنهٔ آن نامتناهی باشد، ولی برد آن تنها یک عضو داشته باشد.
ث دامنه و برد آن نامتناهی باشند.
الف
\({f_1} = \left\{ {\left( {1\:,\:1} \right)\:,\:\left( {2\:,\:2} \right)\:} \right\}\)
ب
\({f_2} = \left\{ {\left( {1\:,\:1} \right)\:,\:\left( {2\:,\:1} \right)\:,\:\left( {3\:,\:1} \right)\:,\:\left( {4\:,\:1} \right)\:} \right\}\)
پ
\({f_3} = \left\{ {\left( {1\:,\:1} \right)\:} \right\}\)
ت
\({f_4} = \left\{ {\left( {1\:,\:1} \right)\:,\:\left( {2\:,\:1} \right)\:,\:\left( {3\:,\:1} \right)\:,\:\left( {4\:,\:1} \right)\:,\:\left( {5\:,\:1} \right)\:,\: \cdots \:} \right\}\)
ث
\({f_5} = \left\{ {\left( {1\:,\:1} \right)\:,\:\left( {2\:,\:2} \right)\:,\:\left( {3\:,\:3} \right)\:,\:\left( {4\:,\:4} \right)\:,\:\left( {5\:,\:5} \right)\:,\: \cdots \:} \right\}\)
3 جاهای خالی در جدول را کامل کنید و نمودار توابعی را که در جدول، توصیف شده اند، رسم کنید.

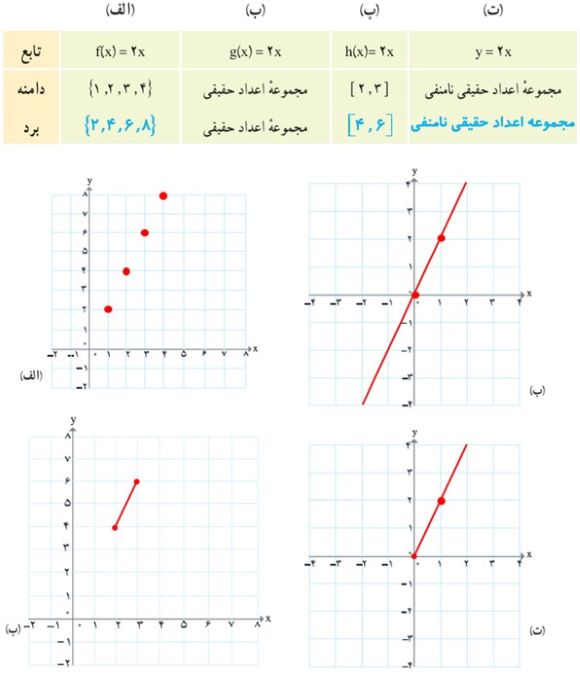
4 یک شمع 20 سانتی متر ارتفاع دارد و در هر ساعت 4 سانتی متر آن می سوزد. پس از چند ساعت شمع خاموش خواهد شد؟ جدولی تنظیم کنید و در ساعات مختلف ارتفاع شمع را محاسبه کنید.

نمودار این تابع را رسم کنید.
چرا این تابع، یک تابع خطی است؟
ساعت \(\frac{{20}}{4} = 5\)
پس از 5 ساعت تمام شمع می سوزد:

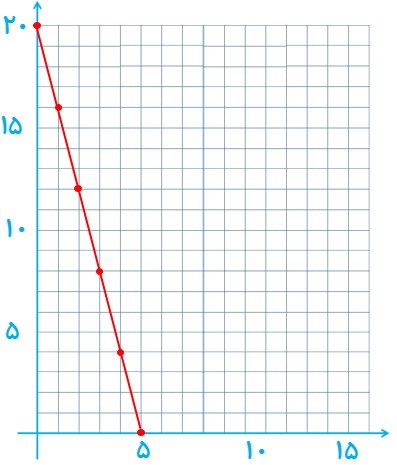
زیرا نمودار آن از یک خط راست می باشد و معادله این خط به صورت زیر است:
y = -4x + 20
5 آیا خط x = 2 را می توان به عنوان یک تابع در نظر گرفت؟ چرا؟ خط y = 5 را چطور؟ در حالت کلی چه موقع یک خط را می توان یک تابع نیز در نظر گرفت؟
خیر؛ زیرا خط 2=x با محور عرض ها موازی است لذا تمام نقاط آن مؤلفه های اول مساوی دارند، ولی 5=y تابع است، زیرا نمودار آن با محور طول ها موازی است و هیچ دو نقطه متمایز آن، مؤلفه های اول یکسان ندارند؛ در حالت کلی، اگر یک خط با محور عرض ها موازی نباشد تابع است.
6 نمایش جبری سه تابع خطی را بنویسید که دامنهٔ آن بازه [-3, 5] باشد. چه تعداد از این گونه توابع وجود دارند؟
\(\begin{array}{*{20}{l}}{y = - 4x + 20\;\;\:;\:x \in \left[ { - 3\:,\:5} \right]}\\{y = 1 - x\;\;\:\;\;\:\:\:{\mkern 1mu} ;\:x \in \left[ { - 3\:,\:5} \right]}\\{y = {x^2}\;\;\:\;\;\:\;\;\:\:\:;\:x \in \left[ { - 3\:,\:5} \right]}\end{array}\)
بی شمار تابع.
7 نمایش جبری تابع زیر را که نمودار آن ارائه شده است، به دست آورید.
از بین نمایش های مختلفی که برای این تابع می دانید، کدام یک مناسب تر است؟
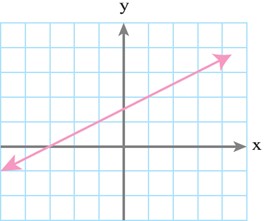
\(\begin{array}{*{20}{l}}{m = \frac{{2 - 0}}{{1 - \left( { - 3} \right)}} = \frac{1}{2}}\\{y - {y_0} = m\left( {x - {x_0}} \right) \Rightarrow y - 2 = \frac{1}{2}\left( {x - 1} \right)}\\{ \Rightarrow y = \frac{1}{2}x + \frac{3}{2}}\end{array}\)
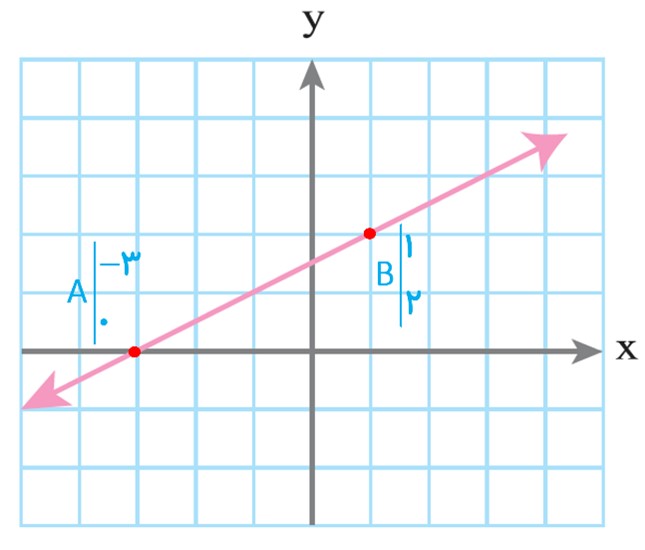
نمایش جبری مناسب تر است؛ زیرا که خلاصه تر است.
8 جدول زیر دمای سنگ ها در عمق های متفاوت زیر سطح زمین را نشان می دهد.

الف توضیح دهید که چرا این جدول یک تابع را به دست می دهد. نمودار آن را رسم کنید.
ب معادله ای برای این تابع به دست آورید.
پ دمای یک سنگ را که در عمق 10 کیلومتری زیرزمین است، بیابید.
الف
زیرا هیچ یک از مؤلفه های اول آن تکرار نشده است.
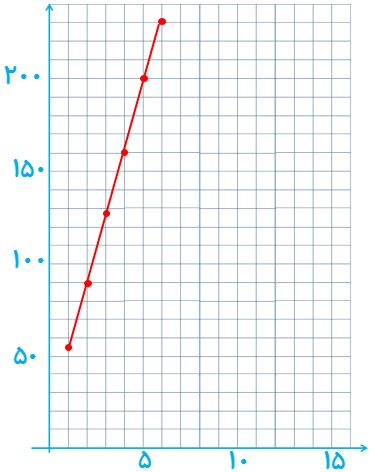
ب
\(\begin{array}{*{20}{l}}{A\left| {\begin{array}{*{20}{l}}1\\{55}\end{array}} \right.}\\{B\left| {\begin{array}{*{20}{l}}2\\{90}\end{array}} \right.}\\{m = \frac{{90 - 55}}{{2 - 1}} = 35}\\{y - {y_0} = m\left( {x - {x_0}} \right) \Rightarrow y - 55 = 35\left( {x - 1} \right)}\\{ \Rightarrow y = 35x + 20}\end{array}\)
پ
y = 35x + 20
\({x_1} = 10 \Rightarrow {y_1} = 370\) درجه سانتی گراد
9
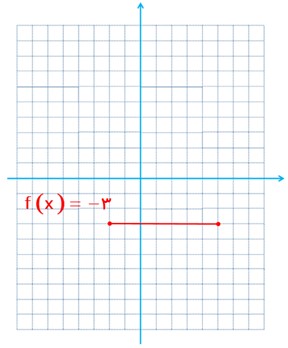
الف تابع f(x) = -3 را رسم کنید و مقادیر f(2) و f(100) و f(-5) و \(f\left( {\sqrt 5 } \right)\) و \(f\left( { - \frac{3}{4}} \right)\) را بدست آورید.
ب اگر دامنهٔ این تابع مجموعهٔ اعداد حقیقی باشد، نمودار تابع را رسم کنید.
پ نمودار این تابع را وقتی که دامنهٔ آن بازهٔ [-2, 5] باشد، نیز رسم کنید.
الف
\(\begin{array}{*{20}{l}}{f\left( x \right) = - 3}\\{ \Rightarrow f\left( 2 \right) = - 3\begin{array}{*{20}{c}}{}&{}\end{array}f\left( {100} \right) = - 3\begin{array}{*{20}{c}}{}&{}\end{array}f\left( { - 5} \right) = - 3\begin{array}{*{20}{c}}{}&{}\end{array}}\\{ \Rightarrow f\left( {\sqrt 5 } \right) = - 3\begin{array}{*{20}{c}}{}&{}\end{array}f\left( { - \frac{3}{4}} \right) = - 3}\end{array}\)
ب
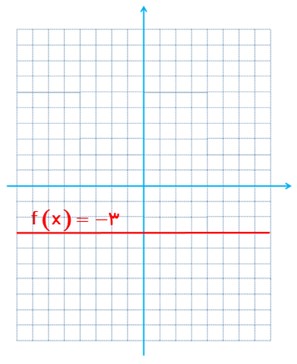
پ
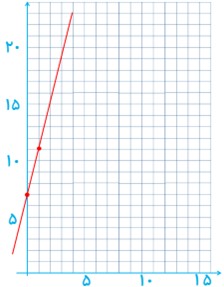
10 برای یک تابع خطی می دانیم که: f(2) = 11 و f(0) = 7 نمودار این تابع را رسم کنید و نمایش جبری آن را بنویسید.
\(\begin{array}{*{20}{l}}{f\left( x \right) = ax + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{f\left( 2 \right) = 11 = 2a + b}\\{f\left( 0 \right) = 7 = b}\end{array}} \right. \Rightarrow a = 2}\\{ \Rightarrow f\left( x \right) = 2x + 7}\end{array}\)
11 آیا جدول زیر یک تابع را نشان می دهد؟ چرا؟

بله؛ زیرا هیچ یک از مؤلفه های اول آن تکرار نشده است.
12 علی در هر دقیقه پیاده روی، مسافت 0/1 کیلومتر را طی می کند. اگر مسافتی را که علی در t دقیقه طی می کند، با f(t) نمایش دهیم، کدام عبارت نمایش جبری این تابع را به دست می دهد؟
الف f(t) = t – 0/1
ب f(t) = 0/1t
پ f(t) = t + 0/1
ت f(t) = 0/1 – t
گزینه (ب) یعنی f(t) = 0/1t نمایش جبری تابع است.
13 اگر درباره تابع g داشته باشیم: \(g:g\left( 0 \right) = 2,\;g\left( 1 \right) = 5,\;g\left( { - 2} \right) = \frac{1}{3},\;g\left( 4 \right) = 3\) را به صورت مجموعه ای از زوج های مرتب بنویسید و نمودار آن را رسم کنید.
\(g = \left\{ {\left( { - 2\:,\:\frac{1}{3}} \right)\:,\:\left( {0\:,\:2} \right)\:,\:\left( {1\:,\:5} \right)\:,\:\left( {4\:,\:3} \right)} \right\}\)

14 برای اندازه گیری دما از واحدهای «سانتی گراد C» و «فارنهایت F» استفاده می شود که با رابطهٔ \(F = \frac{9}{5}C + 32\) به یکدیگر وابسته اند
الف 20 - درجهٔ سانتی گراد، چند درجهٔ فارنهایت است؟
ب 104 درجهٔ فارنهایت چند سانتی گراد است؟
پ معادله ای بنویسید که سانتی گراد را برحسب فارنهایت به دست آورد.
ت آیا رابطهٔ بین این دو واحد، یک تابع خطی را معلوم می کند؟
الف
درجه فارنهایت \(C = - 20 \Rightarrow F = \frac{9}{5}\left( { - 20} \right) + 32 = - 4\)
ب
درجه سانتی گراد \(F = 104 \Rightarrow 104 = \frac{9}{5}\left( C \right) + 32 \Rightarrow C = 40\)
پ
\(F = \frac{9}{5}\left( C \right) + 32 \Rightarrow F - 32 = \frac{9}{5}\left( C \right) \Rightarrow C = \frac{5}{9}\left( {F - 32} \right)\)
ت
بله؛ هر دو تابع هستند.
15 طول یک مستطیل 3 واحد بیشتر از عرض آن است. رابطه ای ریاضی بنویسید که محیط این مستطیل را برحسب تابعی از عرض آن بیان کند.
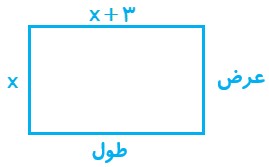
محبط مستطیل = 2 × (طول + عرض) = \(2 \times \left( {\left( {x + 3} \right) + x} \right) = 4x + 6\)
16 دو تابع مثال بزنید که دامنه و برد آنها یکی باشد، ولی هیچ زوج مرتب مشترکی نداشته باشند.
\(\begin{array}{*{20}{l}}{{D_f} = {D_g} = \left\{ {1\:,\:2\:,\:3} \right\}}\\{{R_f} = {R_g} = \left\{ { - 1\:,\: - 2\:,\: - 3} \right\}}\\{f = \left\{ {\left( {1\:,\: - 1} \right)\:,\:\left( {2\:,\: - 2} \right)\:,\:\left( {3\:,\: - 3} \right)} \right\}}\\{g = \left\{ {\left( {1\:,\: - 2} \right)\:,\:\left( {2\:,\: - 3} \right)\:,\:\left( {3\:,\: - 1} \right)} \right\}}\end{array}\)
17 نمودار تابعی را رسم کنید که دامنهٔ آن (0, 2] و برد آن [-2, 1] باشد. چه تعداد از این گونه توابع می توان رسم کرد؟
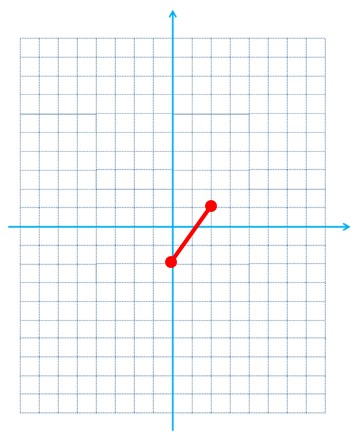
بیشمار تابع
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















