جواب تمرین صفحه 93 درس 4 ریاضی دهم (معادله ها و نامعادله ها)

الف

\(1 < 2x - 3 \le 3 \Rightarrow 4 < 2x \le 6 \Rightarrow 2 < x \le 3 \Rightarrow x \in \left( {\left. {2\,,\,3} \right]} \right.\)

ب

\(\begin{array}{*{20}{l}}\begin{array}{l}x + 1 \le 5 - x < 2x + 3\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x + 1 \le 5 - x \Rightarrow 2x \le 4 \Rightarrow x \le 2 \Rightarrow x \in \left( {\left. { - \infty \,,\,2} \right]} \right.\\\end{array}\\{5 - x < 2x + 3 \Rightarrow 2 < 3x \Rightarrow \frac{2}{3} < x \Rightarrow x \in \left( {\frac{2}{3}\,,\,\infty } \right)}\end{array}} \right.\end{array}\\{}\\{ \Rightarrow x \in \left( {\left. { - \infty \,,\,2} \right]} \right. \cap \left( {\frac{2}{3}\,,\,\infty } \right) \Rightarrow x \in \left( {\left. {\frac{2}{3}\,,\,2} \right]} \right.}\end{array}\)

پ

\(\begin{array}{l} - 2 < \frac{{5 - x}}{2} < 0\,\mathop {\, \Rightarrow }\limits^{ \times \left( { - 1} \right)} \,\,0 < \frac{{x - 5}}{2} < 2\\\\ \Rightarrow 0 < x - 5 < 4 \Rightarrow 5 < x < 9 \Rightarrow x \in \left( {5\,,\,9} \right)\end{array}\)

ت

\(A = \frac{{4 - 2x}}{{3x + 1}} \ge 0\,\,\, \Rightarrow \left\{ {\begin{array}{*{20}{l}}{4 - 2x = 0 \Rightarrow x = 2}\\{3x + 1 = 0 \Rightarrow x = - \frac{1}{3}}\end{array}} \right.\)

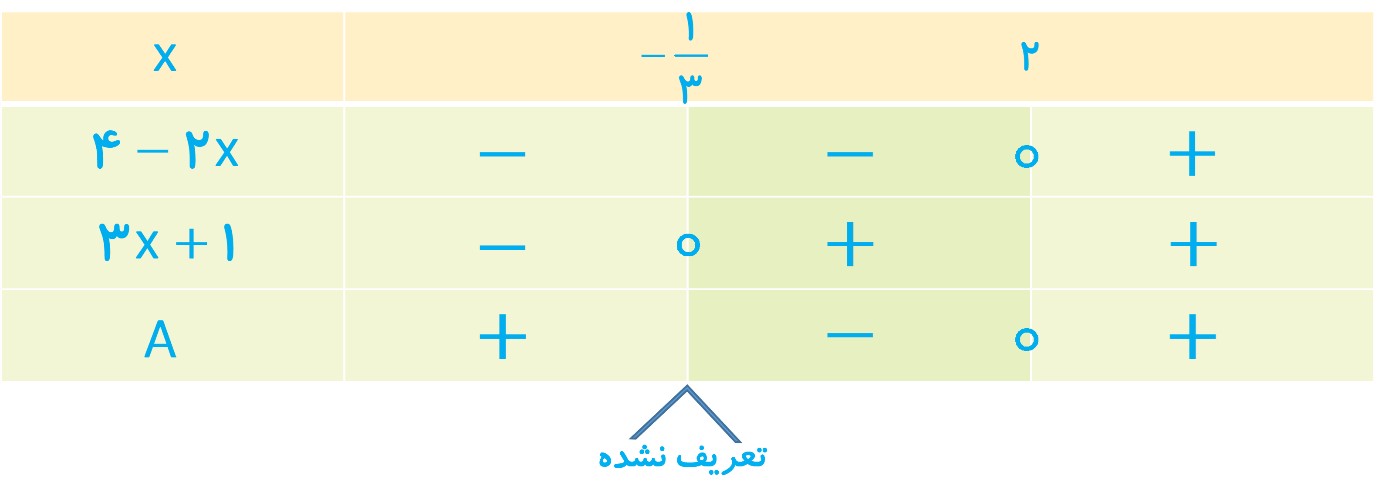
\(x \in ( - \infty \,,\, - \frac{1}{3}) \cup \left[ {\left. {2\,,\,\infty } \right)} \right.\)

ث

\(B = x\left( {{x^2} + 4} \right) < 0\,\, \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} + 4 = 0 \Rightarrow \Delta = {{\left( 0 \right)}^2} - 4\left( 1 \right)\left( 4 \right) = - 16 < 0}\end{array}} \right.\)

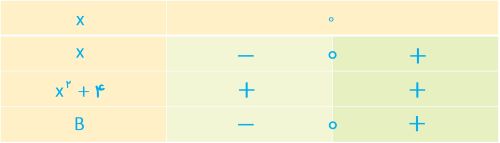
\(x \in \left( { - \infty {\kern 1pt} ,\,0} \right)\)

ج

\(\begin{array}{*{20}{l}}{C = \frac{{{x^3} - x}}{{{x^2} - 2x + 2}} = \frac{{x\left( {{x^2} - 1} \right)}}{{{x^2} - 2x + 2}} \le 0}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 1 = 0 \Rightarrow {x^2} = 1 \Rightarrow x = \pm 1}\\{{x^2} - 2x + 2 = 0 \Rightarrow \Delta = {{\left( { - 2} \right)}^2} - 4\left( 1 \right)\left( 2 \right) = - 4 < 0}\end{array}} \right.}\end{array}\)

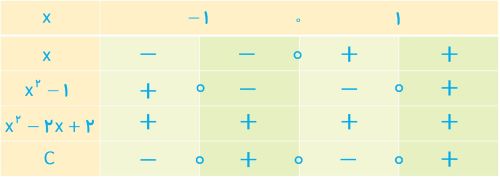
\(x \in \left( {\left. { - \infty {\kern 1pt} ,\, - 1} \right]} \right. \cup \left[ {0\,,\,1} \right]\)

چ

\(\begin{array}{l}\left| {7 - 2x} \right| < 1 \Rightarrow \left| {2x - 7} \right| < 1 \Rightarrow - 1 < 2x - 7 < 1\\\\ \Rightarrow 6 < 2x < 8 \Rightarrow 3 < x < 4 \Rightarrow x \in \left( {3\,,\,4} \right)\end{array}\)

ح

\(\begin{array}{*{20}{l}}\begin{array}{l}\left| {\frac{{x - 1}}{2} - 1} \right| \ge 3 \Rightarrow \left| {\frac{{x - 3}}{2}} \right| \ge 3 \Rightarrow \left| {x - 3} \right| \ge 6\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x - 3 > 6 \Rightarrow x > 9 \Rightarrow x \in \left( {9\,,\,\infty } \right)\\\end{array}\\{x - 3 < - 6 \Rightarrow x < - 3 \Rightarrow x \in \left( { - \infty \,,\, - 3} \right)}\end{array}} \right.\\\end{array}\\{x \in \left( { - \infty \,,\, - 3} \right) \cup \left( {9\,,\,\infty } \right)}\end{array}\)

\(\begin{array}{*{20}{l}}{A = {x^2} + 3x + k}\\{\forall x \in \mathbb{R}:A > 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1 > 0}\\{\Delta < 0}\end{array}} \right.}\\{\Delta < 0 \Rightarrow {b^2} - 4ac > 0 \Rightarrow {{\left( 3 \right)}^2} - 4\left( 1 \right)\left( k \right) < 0}\\{ \Rightarrow 9 - 4k < 0 \Rightarrow k > \frac{9}{4}}\end{array}\)

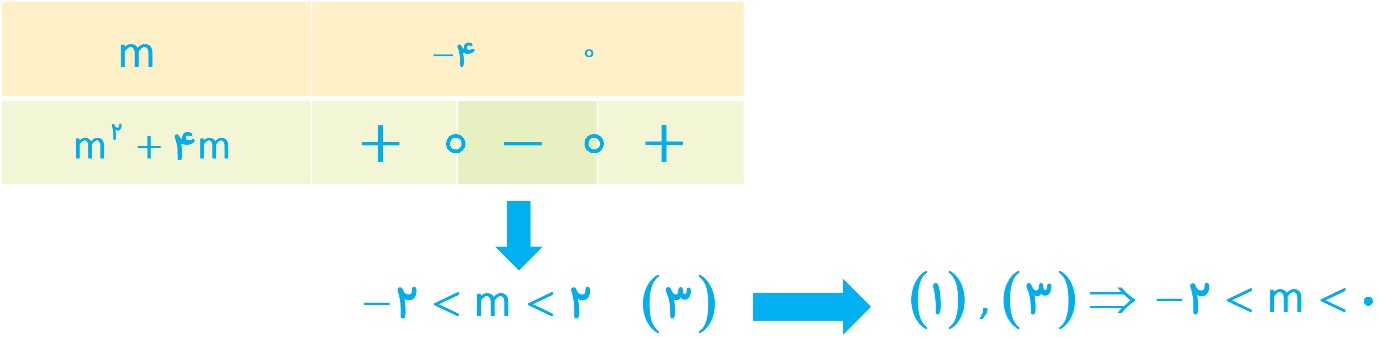
\(\begin{array}{l}y = m{x^2} - mx - 1\\\\\forall x \in \mathbb{R}:y < 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a < 0 \Rightarrow m < 0\;\;{\mkern 1mu} {\kern 1pt} \left( 1 \right)\\\end{array}\\{\Delta < 0 \Rightarrow {b^2} - 4ac < 0 \Rightarrow {m^2} + 4m < 0\;\;{\mkern 1mu} {\kern 1pt} \left( 2 \right)}\end{array}} \right.\\\\\left( 2 \right):\\\\{m^2} + 4m < 0 \Rightarrow {m^2} + 4m = 0\\\\ \Rightarrow m\left( {m + 4} \right) = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 0\\\end{array}\\{m = - 4}\end{array}} \right.\end{array}\)

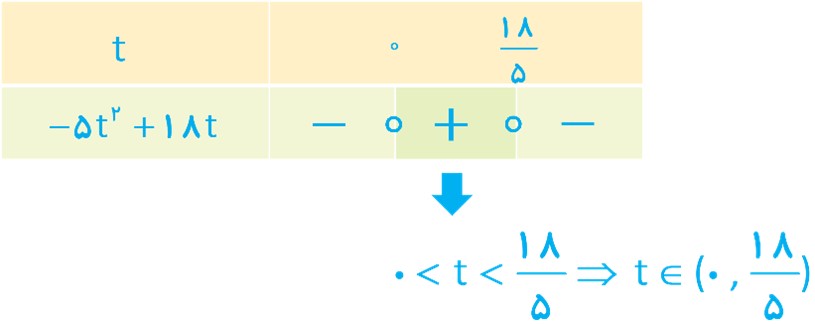
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{h = - 5{t^2} + 18t + 13}\\{h > 13 \Rightarrow t \in \left( {{t_1}\,,\,{t_2}} \right)}\end{array}} \right. \Rightarrow {t_1},{t_2} = ?}\\{ - 5{t^2} + 18t + 13 > 13 \Rightarrow - 5{t^2} + 18t > 0}\\{ \Rightarrow - 5{t^2} + 18t = 0 \Rightarrow t\left( { - 5t + 18} \right) = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{t_1} = 0}\\{ - 5t + 18 = 0 \Rightarrow {t_2} = \frac{{18}}{5}}\end{array}} \right.}\end{array}\)

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}y = \frac{{15}}{8}{x^2} - 30x + 200\\\end{array}\\{y > 110 \Rightarrow x \in ?}\end{array}} \right.\\\\\frac{{15}}{8}{x^2} - 30x + 200 > 110\\\\ \Rightarrow \frac{{15}}{8}{x^2} - 30x + 90 > 0\\\\\frac{{15}}{8}{x^2} - 30x + 90 = 0\\\\ \Rightarrow \Delta = {\left( { - 30} \right)^2} - 4(\frac{{15}}{2})\left( {90} \right) = 900 - 675 = 225 > 0\\\\x = \frac{{ - \left( { - 30} \right) \pm \sqrt {225} }}{{2(\frac{{15}}{8})}} = \frac{{30 \pm 15}}{{\frac{{15}}{4}}} = \\\\\frac{{120 \pm 60}}{{15}} = 8 \pm 4\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 12\\\end{array}\\{x = 4}\end{array}} \right.\end{array}\)