جواب کاردرکلاس صفحه 93 درس 4 ریاضی دهم (معادله ها و نامعادله ها)

الف

\(\begin{array}{l}\left| {\frac{x}{3} + 1} \right| < \frac{2}{3} \Rightarrow \left| {\frac{{x + 3}}{3}} \right| < \frac{2}{3}\\\\ \Rightarrow \left| {x + 3} \right| < 2\\\\ \Rightarrow - 2 < x + 3 < 2 \Rightarrow - 5 < x < - 1\\\\ \Rightarrow x \in \left( { - 5\,,\, - 1} \right)\end{array}\)

ب

\(\begin{array}{l}\left| {5 - 2x} \right| \ge 1 \Rightarrow \left| {2x - 5} \right| \ge 1\\\\ \Rightarrow - 1 \le 2x - 5 \le 1 \Rightarrow 4 \le 2x \le 6\\\\ \Rightarrow 2 \le x \le 3 \Rightarrow x \in \left[ {2\,,\,3} \right]\end{array}\)

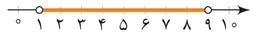
\(\begin{array}{*{20}{l}}{x \in \left( {a\,,\,b} \right) \Leftrightarrow \left| {x - r} \right| < d \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{a + b}}{2}}\\{d = \frac{{b - a}}{2}}\end{array}} \right.}\\{ \Rightarrow x \in \left( {1\,,\,9} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{9 + 1}}{2} = \frac{{10}}{2} = 5}\\{d = \frac{{9 - 1}}{2} = \frac{8}{2} = 4}\end{array}} \right. \Rightarrow \left| {x - 5} \right| < 4}\end{array}\)

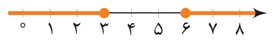
\(\begin{array}{*{20}{l}}{x \in \left( {\left. { - \infty \,,\,a} \right]} \right. \cup \left[ {\left. {b\,,\,\infty } \right)} \right. \Leftrightarrow \left| {x - r} \right| > d \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{a + b}}{2}}\\{d = \frac{{b - a}}{2}}\end{array}} \right.}\\{ \Rightarrow x \in \left( {\left. { - \infty \,,\,3} \right]} \right. \cup \left[ {\left. {6\,,\,\infty } \right)} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{6 + 3}}{2} = \frac{9}{2}}\\{d = \frac{{6 - 3}}{2} = \frac{3}{2}}\end{array}} \right. \Rightarrow \left| {x - \frac{9}{2}} \right| > \frac{3}{2}}\end{array}\)