آیا تمام سوالات فعالیت صفحه 54 ریاضی دهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به فعالیت صفحه 54 ریاضی دهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب فعالیت صفحه 54 درس 3 ریاضی دهم (توان های گویا و عبارت های جبری)

تعداد بازدید : 78.77M

پاسخ فعالیت صفحه 54 ریاضی دهم

گام به گام فعالیت صفحه 54 درس توان های گویا و عبارت های جبری

فعالیت صفحه 54 درس 3

شما در حال مشاهده جواب فعالیت صفحه 54 ریاضی دهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

الف مشابه آنچه که برای ریشه های دوم، سوم، چهارم و پنجم گفته شد، می توان برای ریشه های دیگر مثلاً ریشهٔ ششم نیز عمل کرد. جدول زیر را که مربوط به ریشه های مختلف عدد 64 است، کامل کنید.

ب ریشه های ششم عدد 64 اعداد \( - \sqrt[6]{{64}}\;\;,\;\;\sqrt[6]{{64}}\) یا همان ……… و …………… هستند؛ زیرا \({\left( {\;\;\;\;} \right)^6} = 64\;\;,\;\;{2^6} = 64\) دربارهٔ ریشه های هفتم و هشتم عدد 64 چه می توانید بگویید؟

پ به طور کلی اگر \(n \in N\) دربارهٔ ریشهٔ nاُم عدد 64 چه می توان گفت؟

ت در حالت کلی تر اگر a یک عدد مثبت باشد و \(n \in N\) ، دربارهٔ تعداد ریشه های nام a چه می توان گفت؟

الف

2 و 2-

\({\left( { - 2} \right)^6} = 64\;\;,\;\;{2^6} = 64\)

دارای یک ریشه هفتم و دو ریشه هشتم است.

اگر n فرد باشد، دارای یک ریشه و اگر n زوج باشد، دارای دو ریشه که با هم قرینه اند، است.

برای هر عدد مثبت a ، اگر n فرد باشد، دارای یک ریشه و اگر n زوج باشد، دارای دو ریشه که با هم قرینه اند، است.

الف جدول زیر را که دربارهٔ ریشه های مختلف عدد 64 - است، تکمیل کنید.

ب ریشه های زوج 64 - وجود ندارند؛ زیرا عددی وجود ندارد که به توان …… برسد و مساوی 64 - شود.

پ دربارهٔ ریشه های nام 64- \(\left( {n \in N} \right)\) بحث کنید.

ت اگر a یک عدد منفی و \(n \in N\) باشد، دربارهٔ ریشه nام a چه می توان گفت؟

الف

عدد زوج

اگر n فرد باشد، دارای یک ریشه و اگر n زوج باشد، ریشه نخواهد داشت.

برای هر عدد منفی a، اگر n فرد باشد، دارای یک ریشه و اگر n زوج باشد، ریشه نخواهد داشت.

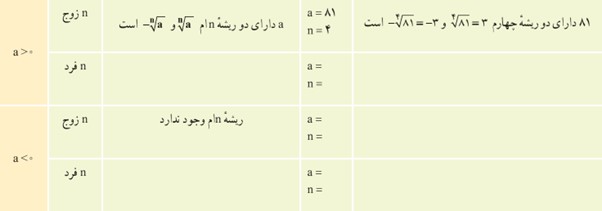
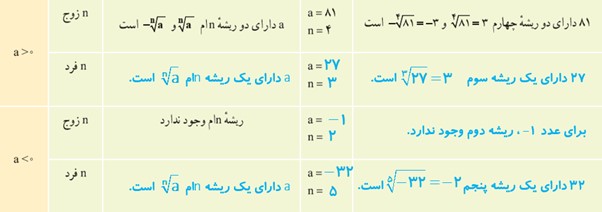
3 جدول زیر را کامل کنید.

4 در پایه نهم دیدید که:

برای هر دو عدد مثبت a و b : \(\sqrt a \times \sqrt b = \sqrt {ab} \)

برای هر دو عدد مثبت a و b : \(\sqrt[3]{a} \times \sqrt[3]{b} = \sqrt[3]{{ab}}\)

الف آیا رابطهٔ بالا دربارهٔ \(\sqrt[4]{a} \times \sqrt[4]{b}\) نیز برقرار می باشد؟ مثال بزنید.

ب با توجه به اینکه 4 یک عدد زوج است، باید a و b ............. باشند.

\(\begin{array}{l}\sqrt[4]{{16}} \times \sqrt[4]{{81}} = 2 \times 3 = .........\\\sqrt[4]{{16}} \times \sqrt[4]{{81}} = \sqrt[4]{{\,.............\,}} = 6\end{array}\)

پ دربارهٔ \(\sqrt[5]{a} \times \sqrt[5]{b} = \sqrt[5]{{ab}}\) چه می توان گفت؟

ت آیا a و b حتماً باید نامنفی باشند؟ مثالی از a و b نامنفی و مثالی از a و b منفی ارائه کنید و نشان دهید تساوی همواره برقرار است.

الف

بله ، برقرار است:

\(\begin{array}{*{20}{l}}{6 = \sqrt[4]{{1296}} = \sqrt[4]{{16 \times 81}} = }\\{}\\{\sqrt[4]{{16}} \times \sqrt[4]{{81}} = 2 \times 3 = 6}\end{array}\)

مثبت

\(\begin{array}{l}\sqrt[4]{{16}} \times \sqrt[4]{{81}} = 2 \times 3 = 6\\\\\sqrt[4]{{16}} \times \sqrt[4]{{81}} = \sqrt[4]{{16 \times 81}} = 6\end{array}\)

این تساوی نیز برقرار است.

خیر؛ a و b می تواند هر عدد مثبت و منفی باشند:

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = 32\\\end{array}\\{b = 243}\end{array}} \right.\\\\ \Rightarrow 6 = \sqrt[5]{{7776}} = \sqrt[5]{{32 \times 243}} = \\\\\sqrt[5]{{32}} \times \sqrt[5]{{243}} = 2 \times 3 = 6\\\\\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = - 32\\\end{array}\\{b = - 100000}\end{array}} \right.\\\\\begin{array}{*{20}{l}}{ \Rightarrow 20 = \sqrt[5]{{3200000}} = \sqrt[5]{{\left( { - 32} \right) \times \left( { - 100000} \right)}} = }\\{}\\{\sqrt[5]{{\left( { - 32} \right)}} \times \sqrt[5]{{\left( { - 100000} \right)}} = \left( { - 2} \right) \times \left( { - 10} \right) = 20}\end{array}\end{array}\)