جواب تمرین صفحه 45 درس 2 ریاضی دهم (مثلثات)

ربع دوم \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\cos \alpha < 0}\\{\sin {\mkern 1mu} {\mkern 1mu} \alpha > 0}\end{array}} \right.\)

\(\begin{array}{l} \Rightarrow \sin {\mkern 1mu} {\mkern 1mu} \alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - \frac{9}{{25}}} = \sqrt {\frac{{16}}{{25}}} = \frac{4}{5}\\\\\tan \alpha = \frac{{\sin {\mkern 1mu} {\mkern 1mu} \alpha }}{{\cos \alpha }} = - \frac{4}{3}\\\\\cot \alpha = \frac{{\cos \alpha }}{{\sin {\mkern 1mu} {\mkern 1mu} \alpha }} = - \frac{3}{4}\end{array}\)

ربع چهارم  \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\cos \alpha > 0}\\{\sin {\mkern 1mu} {\mkern 1mu} \alpha < 0}\end{array}} \right.\)

\(\begin{array}{l}1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow {\cos ^2}\alpha = \frac{1}{{1 + {{\tan }^2}\alpha }} = \frac{9}{{25}}\\\\ \Rightarrow \cos \alpha = \frac{3}{5}\\\\\sin \:\alpha = - \sqrt {1 - {{\cos }^2}\alpha } = - \sqrt {\frac{{16}}{{25}}} = - \frac{4}{5}\\\\\cot \alpha = \frac{1}{{\tan \alpha }} = - \frac{3}{4}\end{array}\)

\(90^\circ < 135^\circ < 180^\circ \Rightarrow \)

ربع دوم \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\cos 135^\circ > 0}\\{\sin {\mkern 1mu} {\mkern 1mu} 135^\circ < 0}\end{array}} \right.\)

\(\begin{array}{l}\cos 135^\circ = - \sqrt {1 - {{\sin }^2}135^\circ } = - \sqrt {1 - \frac{1}{2}} = - \frac{{\sqrt 2 }}{2}\\\\\tan 135^\circ = \frac{{\sin {\mkern 1mu} {\mkern 1mu} 135^\circ }}{{\cos 135^\circ }} = - 1\\\\\cot \alpha = \frac{{\cos 135^\circ }}{{\sin {\mkern 1mu} {\mkern 1mu} 135^\circ }} = - 1\end{array}\)

\(180^\circ < 240^\circ < 270^\circ \Rightarrow \)

ربع چهارم \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\cos 240^\circ < 0}\\{\sin {\mkern 1mu} {\mkern 1mu} 240^\circ < 0}\end{array}} \right.\)

\(\begin{array}{l}1 + {\tan ^2}240^\circ = \frac{1}{{{{\cos }^2}240^\circ }} \Rightarrow {\cos ^2}240^\circ = \frac{1}{{1 + {{\tan }^2}240^\circ }} = \frac{1}{4}\\\\ \Rightarrow \cos 240^\circ = - \frac{1}{2}\\\\\sin \:240^\circ = - \sqrt {1 - {{\cos }^2}240^\circ } = - \sqrt {1 - \frac{1}{4}} = - \frac{{\sqrt 3 }}{2}\\\\\cot 240^\circ = \frac{1}{{\tan 240^\circ }} = \frac{1}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\end{array}\)

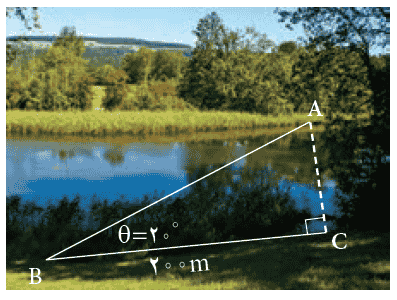
\(\begin{array}{l}\sin \:20^\circ \simeq 0/34\\\\ \Rightarrow \cos \:20^\circ = \sqrt {1 - {{\sin }^2}\:20^\circ } = \sqrt {1 - {{\left( {0/34} \right)}^2}} \simeq 0/94\\\\\tan \:20^\circ = \frac{{AC}}{{BC}} = \frac{{\sin \:20^\circ }}{{\cos \:20^\circ }} \simeq 0/36\\\\AC = BC \times \tan \:20^\circ = 200 \times 0/36 = 72\end{array}\)

الف \(\frac{1}{{\sin \theta }} \times \tan \theta = \frac{1}{{\cos \theta }}\)

طرف چپ :

\(\frac{1}{{\sin \theta }} \times \tan \theta = \frac{1}{{\sin \theta }} \times \frac{{\sin \theta }}{{\cos \theta }}\) 

\( = \frac{1}{{\cos \theta }}\) : طرف راست

ب \(\frac{{\cos \theta }}{{1 + \sin \theta }} = \frac{{1 - \sin \theta }}{{\cos \theta }}\)

طرف چپ :

\(\begin{array}{l}\frac{{\cos \theta }}{{1 + \sin \theta }} = \frac{{\cos \theta }}{{1 + \sin \theta }} \times \frac{{1 - \sin \theta }}{{1 - \sin \theta }}\\\\ = \frac{{\cos \theta \left( {1 - \sin \theta } \right)}}{{1 - {{\sin }^2}\theta }} = \frac{{\cos \theta \left( {1 - \sin \theta } \right)}}{{{{\cos }^2}\theta }}\end{array}\)

\( = \frac{{1 - \sin \theta }}{{\cos \theta }}\)  : طرف راست

پ \(\frac{{1 + \tan \alpha }}{{1 + \cot \alpha }} = \tan \alpha \)

طرف چپ :

\(\frac{{1 + \tan \alpha }}{{1 + \cot \alpha }} = \frac{{1 + \frac{{\sin \alpha }}{{\cos \alpha }}}}{{1 + \frac{{\cos \alpha }}{{\sin \alpha }}}} = \frac{{\frac{{\cos \alpha + \sin \alpha }}{{\cos \alpha }}}}{{\frac{{\sin \alpha + \cos \alpha }}{{sin\alpha }}}} = \frac{{sin\alpha }}{{\cos \alpha }}\) 

\( = \tan \alpha \) : طرف راست

ت \(1 - \frac{{{{\cos }^2}x}}{{1 + \sin x}} = \sin x\)

طرف چپ :

\(1 - \frac{{{{\cos }^2}\:x}}{{1 + \sin \:x}} = 1 - \frac{{1 - si{n^2}\:x}}{{1 + \sin \:x}} = 1 - \frac{{\left( {1 + sin\:x} \right)\left( {1 - sin\:x} \right)}}{{1 + \sin \:x}}\)

\( = 1 - \left( {1 - sin\:x} \right) = sin\:x\) : طرف راست

ث \(\frac{1}{{\cos x}} - \tan x = \frac{{\cos x}}{{1 + \sin x}}\)

طرف چپ :

\(\begin{array}{l}\frac{1}{{\cos \:x}} - \tan \:x = \frac{1}{{\cos \:x}} - \frac{{\sin \:x}}{{\cos \:x}} = \frac{{1 - \sin \:x}}{{\cos \:x}}\\\\ = \frac{{1 - \sin \:x}}{{\cos \:x}} \times \frac{{1 + \sin \:x}}{{1 + \sin \:x}} = \frac{{1 - {{\sin }^2}\:x}}{{\cos \:x\left( {1 + \sin \:x} \right)}}\end{array}\)

\({ = \frac{{{{\cos }^2}\:x}}{{\cos \:x\left( {1 + \sin \:x} \right)}} = \frac{{\cos \:x}}{{1 + \sin \:x}}}\)  : طرف راست