جواب تمرین صفحه 40 درس 2 ریاضی دهم (مثلثات)
تعداد بازدید : 86.39Mپاسخ تمرین صفحه 40 ریاضی دهم
-گام به گام تمرین صفحه 40 درس مثلثات
-تمرین صفحه 40 درس 2
-شما در حال مشاهده جواب تمرین صفحه 40 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
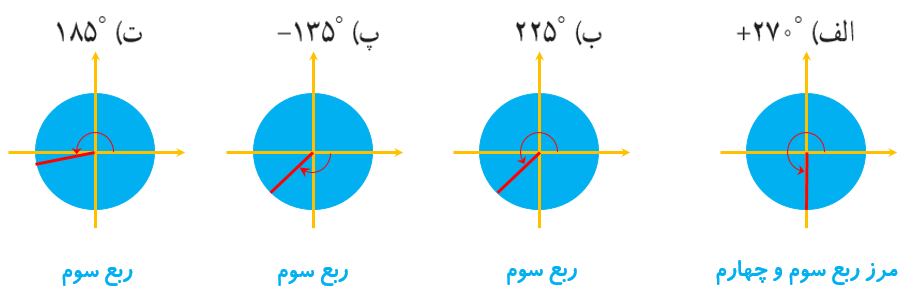
1 هر یک از زاویه های زیر را روی دایرهٔ مثلثاتی رسم کنید، سپس مشخص کنید در کدام یک از نواحی چهارگانه قرار می گیرد.
الف °270+
ب °225
پ °135-
ت °185
2 در هر یک از موارد زیر، نسبت مثلثاتی زاویه ای داده شده است. سایر نسبت های مثلثاتی را به دست آورید.
الف \(\cos \alpha = \frac{3}{7}\) (α در ربع چهارم)
ب \(\sin \beta = \frac{{ - 1}}{2}\) (\(\beta \) در ربع سوم)
الف
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{x > 0}\\{y < 0}\end{array}} \right. \Rightarrow x = \frac{3}{7} \Rightarrow {x^2} + {y^2} = 1\\\\ \Rightarrow {\left( {\frac{3}{7}} \right)^2} + {y^2} = 1 \Rightarrow {y^2} = 1 - \frac{9}{{49}} = \frac{{40}}{{49}}\\\\ \Rightarrow y = - {\mkern 1mu} \frac{{\sqrt {40} }}{7}\\\\\sin {\mkern 1mu} \alpha = - {\mkern 1mu} {\mkern 1mu} \frac{{\sqrt {40} }}{7}\\\\\tan {\mkern 1mu} \alpha = - {\mkern 1mu} {\mkern 1mu} \frac{{\sqrt {40} }}{3}\\\\\cot \alpha = - {\mkern 1mu} {\mkern 1mu} \frac{3}{{\sqrt {40} }}\end{array}\)
ب
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{x < 0}\\{y < 0}\end{array}} \right. \Rightarrow y = - {\mkern 1mu} {\mkern 1mu} \frac{1}{2} \Rightarrow {x^2} + {y^2} = 1\\\\ \Rightarrow {x^2} + {\left( { - {\mkern 1mu} {\mkern 1mu} \frac{1}{2}} \right)^2} = 1 \Rightarrow {x^2} = 1 - \frac{1}{4} = \frac{3}{4}\\\\ \Rightarrow x = - {\mkern 1mu} \frac{{\sqrt 3 }}{2}\\\\\cos {\mkern 1mu} \beta = - {\mkern 1mu} {\mkern 1mu} \frac{{\sqrt 3 }}{2}\\\\\tan {\mkern 1mu} \beta = \frac{1}{{\sqrt 3 }}\\\\\cot \beta = \frac{{\sqrt 3 }}{1} = \sqrt 3 \end{array}\)
3 اگر θtan و θsin هم علامت باشند، آنگاه θ در کدام ربع مثلثاتی قرار دارد؟
ممکن است در ربع اول و یا چهارم باشد؛ زیرا در این نواحی sin و tan هم علامت هستند.
4 حدود زاویهٔ θ را در هر یک از حالات زیر مشخص کنید.
الف \(\sin \theta > 0\,\,,\,\,\cos \theta > 0\)
ب \(\sin \theta < 0\,\,,\,\,\cos \theta > 0\)
الف
0° < θ < 90°
ب
270° < θ < 360°
5 اگر \(\sin \alpha \times \cos \alpha < 0\)، آنگاه α در کدام یک از نواحی چهارگانه می تواند قرار بگیرد؟ چرا؟
در ربع دوم و یا چهارم؛ زیرا:
\(\sin {\mkern 1mu} \alpha \times \cos \alpha < 0\)
\(\left. {\begin{array}{*{20}{l}}{\sin {\mkern 1mu} \alpha > 0}\\{\cos \alpha < 0}\end{array}} \right\} \Rightarrow \) ربع دوم:
\(\left. {\begin{array}{*{20}{l}}{\sin {\mkern 1mu} \alpha < 0}\\{\cos \alpha > 0}\end{array}} \right\} \Rightarrow \) ربع چهارم:
6 زاویه ای مثل α پیدا کنید به طوری که \(tan\alpha > cot\alpha \) اکنون زاویه ای مثل \(\beta \) پیدا کنید، به طوری که \({\rm{cot}}\beta {\rm{ > tan}}\beta {\rm{ }}\) از این تمرین چه نتیجه ای می گیرید؟
\(\begin{array}{l}\alpha = 60^\circ \Rightarrow \tan \:\alpha > \cot \:\alpha \\\\\beta = 30^\circ \Rightarrow \tan \:\beta < \cot \:\beta \end{array}\)
نتیجه می گیریم که اگر زاویه بین 0 تا 45 درجه باشد، cot از tan بیشتر است و اگر زاویه بین 45 تا 90 درجه باشد، tan از cot بیشتر است.
7 در تمرین ٦ به جای تانژانت و کتانژانت به ترتیب سینوس و کسینوس قرار دهید و در مورد آن بحث کنید.
\(\begin{array}{l}\alpha = 60^\circ \Rightarrow \sin \:\alpha > \cos \:\alpha \\\\\beta = 30^\circ \Rightarrow \sin \:\beta < \cos \:\beta \end{array}\)
نتیجه می گیریم که اگر زاویه بین 0 تا 45 درجه باشد، cos از sin بیشتر است و اگر زاویه بین 45 تا 90 درجه باشد، sin از cos بیشتر است.
8 معادلهٔ خطی را بنویسید که زاویهٔ آن با جهت مثبت محور xها °45 است و نقطهٔ (0,2) روی آن قرار دارد.
\(\begin{array}{l}y - {y_0} = m\left( {x - {x_0}} \right)\\\\\left. {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{y_0} = 2}\\{m = \tan {\mkern 1mu} 45^\circ = 1}\end{array}} \right\}\\\\ \Rightarrow y - 2 = 1\left( {x - 0} \right) \Rightarrow y = x + 2\end{array}\)
9 با توجه به شکل زیر، معادلهٔ خط l را به دست آورید.

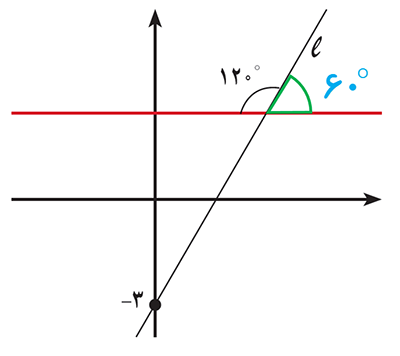
\(\begin{array}{l}y - {y_0} = m\left( {x - {x_0}} \right)\\\\\left. {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{y_0} = - 3}\\{m = \tan {\mkern 1mu} \:60^\circ = \sqrt 3 }\end{array}} \right\}\\\\ \Rightarrow y + 3 = \sqrt 3 \left( {x - {\mkern 1mu} {\mkern 1mu} 0} \right) \Rightarrow y = \sqrt 3 x - 3\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















