1736019749.png)
جواب فعالیت صفحه 33 درس 2 ریاضی دهم (مثلثات)
تعداد بازدید : 78.77Mپاسخ فعالیت صفحه 33 ریاضی دهم
-گام به گام فعالیت صفحه 33 درس مثلثات
-فعالیت صفحه 33 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 33 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 یک زاویهٔ °50 رسم کنید. با تشکیل یک مثلث قائم الزاویه و اندازه گیری طول های موردنظر با یک خط کش مدرج، نسبت های مثلثاتی زاویه °50 را به صورت تقریبی حساب کنید. سپس با ماشین حساب، مقادیر واقعی را به دست آورید و با مقادیر قبل مقایسه کنید.
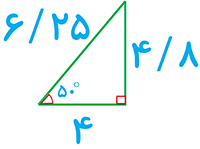
مقادیر تقریبی:
\(\begin{array}{l}\sin \left( {50^\circ } \right) = \frac{{4/8}}{{6/25}} = 0/768\\\\\cos \left( {50^\circ } \right) = \frac{4}{{6/25}} = 0/64\\\\\tan \left( {50^\circ } \right) = \frac{{4/8}}{4} = 1/2\\\\{\mkern 1mu} \cot \left( {50^\circ } \right) = \frac{4}{{4/8}} = 0/833\end{array}\)
مقادیر ماشین حساب :
\(\begin{array}{l}\sin \left( {50^\circ } \right) = 0/766\\\\\cos \left( {50^\circ } \right) = 0/643\\\\\tan \left( {50^\circ } \right) = 1/191\\\\\cot \left( {50^\circ } \right) = 0/839\end{array}\)
2 می خواهیم مساحت مثلث ABC در شکل زیر را پیدا کنیم. می دانیم:
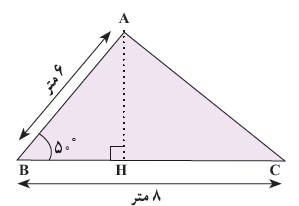
مساحت مثلث ABC = ارتفاع × قاعده × \(\frac{1}{2}\)
الف با توجه به اینکه sin50°=0/76 داریم:
\(\sin 50^\circ = \frac{{AH}}{{(vatar)}} = \frac{{AH}}{{}}\;\; \Rightarrow \;AH = ........\)
ب با توجه به قسمت (الف) داریم:
مساحت مثلث ABC =
\(\frac{1}{2}AH\; \times \;BC = \frac{1}{2}\; \times \;......\; \times \;......\; = \;......\;\)
الف
\(sin50^\circ = \frac{{AH}}{6}\:\: \Rightarrow \:AH = \:6 \times \sin \left( {50^\circ } \right) \simeq 4/6\)
ب مساحت مثلث ABC
\(\frac{1}{2}AH \times BC = \frac{1}{2} \times 6 \times 4/5 \simeq 13/5\)
3 در هر مثلث، با معلوم بودن مقادیر طول دو ضلع مثلث و اندازهٔ زاویهٔ بین آنها نشان دهید:
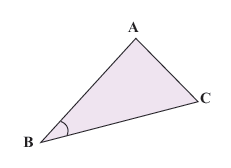
مساحت مثلث ABC =
\(\frac{1}{2} \times AB \times BC \times \sin B\)
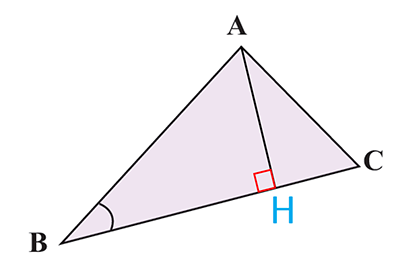
\(\begin{array}{*{20}{l}}{\left. {\begin{array}{*{20}{l}}{{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AH \times BC}\\\begin{array}{l}\\\sin {\mkern 1mu} B = \frac{{AH}}{{AB}} \Rightarrow AH = AB \times \sin {\mkern 1mu} B\end{array}\end{array}} \right\}}\\{}\\{ \Rightarrow {S_{A\mathop B\limits^\Delta C}} = \frac{1}{2} \times AB \times BC \times \sin {\mkern 1mu} B}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
