جواب کاردرکلاس صفحه 122 درس 6 ریاضی دهم (شمارش، بدون شمردن)
تعداد بازدید : 86.39Mپاسخ کاردرکلاس صفحه 122 ریاضی دهم
-گام به گام کاردرکلاس صفحه 122 درس شمارش، بدون شمردن
-کاردرکلاس صفحه 122 درس 6
-شما در حال مشاهده جواب کاردرکلاس صفحه 122 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
الف با سه رقم 5 و 3 و 2 چند عدد سه رقمی می توان نوشت؟ به طور مثال 235 و 352 و 335 سه نمونه از این اعدادند. برای این کار می توان نوشتن عدد سه رقمی را به صورت پرکردن سه جایگاه مقابل با ارقام مذکور درنظر گرفت.

پس این کار سه مرحله دارد و هر سه مرحلهٔ آن باید انجام شود، برای به دست آوردن جواب، تعداد راه های پرکردن هر جایگاه باید مشخص شود و با استفاده از اصل ضرب درهم ضرب شود.
هر جایگاه را به سه حالت می توان پر کرد؛ لذا 27 عدد وجود دارد.

با نمودار درختی در سال های پیش آشنا شده اید. از این نمودار نیز می توان برای به دست آوردن تعداد اعداد موردنظر و نیز نوعی از نمایش آنها استفاده کرد.به نمودار درختی کشیده شده در حاشیهٔ صفحه دقت و آن را تکمیل کنید.

ب با همان سه رقم چند عدد سه رقمی می توان ساخت که رقم تکراری نداشته باشد؟
1 برای پرکردن جایگاه اول از سمت چپ )صدگان( چند حالت امکان دارد؟

2 حال فرض کنیم یکی از اعداد را در اولین جایگاه گذاشته ایم. برای پرکردن جایگاه دوم چند حالت امکان دارد؟

3 برای پرکردن جایگاه سوم چند حالت وجود دارد؟
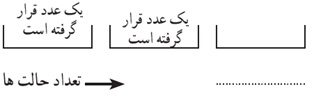
لذا …… = …… × …… × …… عدد سه رقمی توسط 2 و 3 و 5 با ارقام غیرتکراری وجود دارد.
پ با همان سه عدد چند عدد سه رقمی زوج می توان نوشت؟
1 جایگاه سمت راست به چند روش می تواند پر شود، به گونه ای که عدد ساخته شده زوج باشد؟

2 دو جایگاه ؟دیگر هر یک به چند روش می توانند، پر شوند؟
لذا تعداد اعداد در این حالت برابر است با …… = …… × …… × ……
ت با همان سه عدد چند عدد سه رقمی زوج با ارقام غیرتکراری می توان نوشت؟
1 جایگاه سمت راست به چند روش می تواند پر شود به گونه ای که عدد ساخته شده زوج باشد

2 پس از پرکردن جایگاه سمت راست، جایگاه سمت چپ، به چند طریق می تواند پر شود؟
3 حال جایگاه وسط به چند طریق می تواند پرشود؟
4 لذا تعداد اعداد مورد نظر در این حالت برابر است با …… = …… × …… × ……
الف
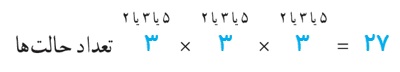

ب
1

2

3 لذا 27 = 3 × 3 × 3 عدد سه رقمی توسط 2 و 3 و 5 با ارقام غیرتکراری وجود دارد.

پ
1 در این جایگاه فقط عدد 2 می تواند قرار بگیرد.
2 در جایگاه های دیگر هر کدام از این 3 عدد می تواند قرار بگیرند، پس هر کدام دارای 3 حالت است.
لذا تعداد اعداد در این حالت برابر است با 6 = 1 × 2 × 3
ت
1

2 در جایگاه سمت چپ فقط یکی از اعداد 3 یا 5 می توانند باشند، پس 2 حالت داریم.
3 با قرار گرفتن یکی از اعداد 3 یا 5 در جایگاه سمت چپ، فقط یک عدد برای جایگاه وسط باقی
می ماند، لذا در این جایگاه فقط 1 حالت داریم.
4 لذا تعداد اعداد مورد نظر در این حالت برابر است با 2 = 1 × 1 × 1
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















