جواب تمرین صفحه 63 درس 3 ریاضی یازدهم تجربی (تابع)
تعداد بازدید : 86.59Mپاسخ تمرین صفحه 63 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 63 درس تابع
-تمرین صفحه 63 درس 3
-شما در حال مشاهده جواب تمرین صفحه 63 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 وارون تابع \(f = \left\{ {\left( {2,3} \right)\;,\;\left( { - 2,1} \right)\;,\;\left( { - 1,2} \right)} \right\}\) را به دست آورید.
\(f = \left\{ {\left( {2\;,\;3} \right)\;,\;\left( { - 2\;,\;1} \right)\;,\;\left( { - 1\;,\;2} \right)} \right\} \Rightarrow {f^{ - 1}} = \left\{ {\left( {3\;,\;2} \right)\;,\;\left( {1\;,\; - 2} \right)\;,\;\left( {2\;,\; - 1} \right)} \right\}\)
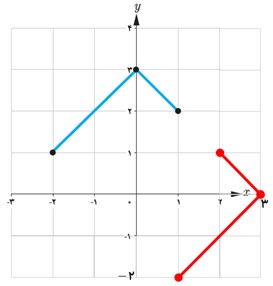
2 نمودار وارون تابع داده شده در شکل مقابل را رسم کنید.

3 ضابطهٔ وارون هر یک از توابع با ضابطه های زیر را بیابید.
الف \(f\left( x \right) = 5x - 2\)
ب \(f\left( x \right) = \frac{3}{5}x + 4\)
پ \(f\left( x \right) = \frac{{ - 7x + 3}}{5}\)
الف
\(\begin{array}{l}f\left( x \right) = 5x - 2 \Rightarrow y = 5x - 2\\\\ \Rightarrow 5x = y + 2 \Rightarrow x = \frac{1}{5}y + \frac{2}{5}\\\\ \Rightarrow {f^{ - 1}}\left( y \right) = \frac{1}{5}y + \frac{2}{5}\\\\ \Rightarrow {f^{ - 1}}\left( x \right) = \frac{1}{5}x + \frac{2}{5}\end{array}\)
ب
\(\begin{array}{l}f\left( x \right) = \frac{3}{5}x + 4 \Rightarrow y = \frac{3}{5}x + 4\\\\ \Rightarrow \frac{3}{5}x = y - 4 \Rightarrow x = \frac{5}{3}y - \frac{{20}}{3}\\\\ \Rightarrow {f^{ - 1}}\left( y \right) = \frac{5}{3}y - \frac{{20}}{3}\\\\ \Rightarrow {f^{ - 1}}\left( x \right) = \frac{5}{3}x - \frac{{20}}{3}\end{array}\)
پ
\(\begin{array}{l}f\left( x \right) = \frac{{ - 7x + 3}}{5} \Rightarrow y = \frac{{ - 7x + 3}}{5}\\\\ \Rightarrow - 7x + 3 = 5y \Rightarrow - 7x = 5y - 3\\\\ \Rightarrow x = - \frac{5}{7}y + \frac{3}{7}\\\\ \Rightarrow {f^{ - 1}}\left( y \right) = - \frac{5}{7}y + \frac{3}{7}\\\\ \Rightarrow {f^{ - 1}}\left( x \right) = - \frac{5}{7}x + \frac{3}{7}\end{array}\)
4 می خواهیم با حذف تعدادی از نقاط نمودار مقابل، آن را به یک تابع یک به یک تبدیل کنیم. حداکثر چند نقطه می تواند باقی بماند؟
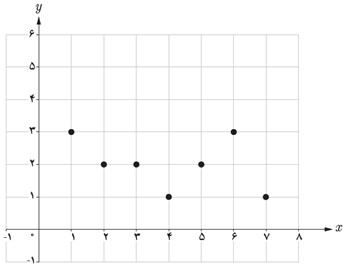
حداکثر سه نقطه می تواند باقی بماند؛ زیرا می دانیم که اگر در نمودار تابع یک به یک اگر خطی موازی محور طول ها رسم کنیم، نمودار را تنها در یک نقطه قطع خواهد کرد. در نتیجه:

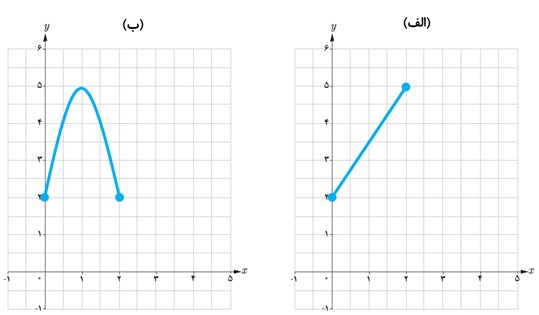
5 نمودار تابعی با دامنهٔ [0,2] و برد [2,5] را رسم کنید:
الف به شرطی که این تابع یک به یک باشد.
ب به شرطی که این تابع یک به یک نباشد.
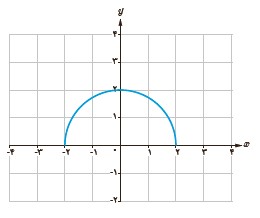
6 با حذف بخشی از نمودار نیم دایرهٔ داده شده، نمودار یک تابع یک به یک را مشخص کنید.

مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















