آیا تمام سوالات تمرین صفحه 77 حسابان یازدهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به تمرین صفحه 77 حسابان یازدهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب تمرین صفحه 77 درس 3 حسابان یازدهم (توابع نمایی و لگاریتمی)

تعداد بازدید : 78.86M

پاسخ تمرین صفحه 77 حسابان یازدهم

گام به گام تمرین صفحه 77 درس توابع نمایی و لگاریتمی

تمرین صفحه 77 درس 3

شما در حال مشاهده جواب تمرین صفحه 77 حسابان یازدهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

1 تحت شرایط ایده آل، جرم یک تودهٔ معین از باکتری ها در هر ساعت دو برابر می شود. فرض کنید در ابتدا 100 میلی گرم باکتری وجود دارد.

الف جرم توده پس از t ساعت را به صورت یک تابع نمایی بنویسید.

ب جرم توده را پس از 20 ساعت برآورد کنید.

الف

\(m\left( t \right) = 100{\left( 2 \right)^t}\)

\(t = 20 \Rightarrow m\left( {20} \right) = 100{\left( 2 \right)^{20}}\)

2 نمودار توابع \(y = {2^x} - 1\;\;,\;y = {2^x} + 1\;\;,\;\;y = {2^x}\) در شکل روبه رو آمده اند. ضابطه هر تابع را روی آن مشخص کنید. با مقایسه نمودارهای توابع \(y = {a^x} - 2\;\;,\;\;y = {a^x} + 2\;\;,\;\;y = {a^x}\) با یکدیگر چه نتیجه ای می گیرید؟ (a>1)

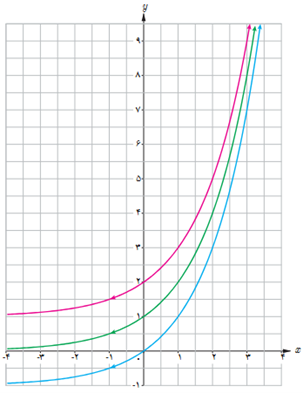
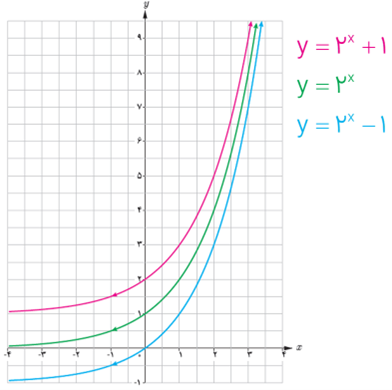
ابتدا نمودار \(y = {a^x}\) را رسم می کنیم و سپس 2 واحد آن را در جهت بالا انتقال می دهیم و در این صورت نمودار \(y = {a^x} + 2\) بدست می آید و اگر نمودار \(y = {a^x}\) را 2 واحد به سمت پایین انتقال دهیم، نمودار\(y = {a^x} - 2\) رسم می شود.

3 داروها در بدن با ادرار دفع می شوند. فرض کنید 10 میلی گرم از یک نوع دارو در بدن شخصی قرار دارد و مقدار آن پس از t ساعت از رابطه \(A\left( t \right) = 10{\left( {0/8} \right)^t}\) به دست می آید.

الف مقدار دارو پس از 8 ساعت چقدر است؟

ب چه درصدی از دارو در هر ساعت از بین می رود؟

الف

\(A\left( 8 \right) = 10{\left( {0/8} \right)^8} \simeq 1/7\)

\(\begin{array}{l}\left| {\frac{{A\left( {t + 1} \right) - A\left( t \right)}}{{A\left( t \right)}}} \right| \times 100 = \left| {\frac{{10{{\left( {0/8} \right)}^{t + 1}} - 10{{\left( {0/8} \right)}^t}}}{{10{{\left( {0/8} \right)}^t}}}} \right| \times 100\\\\ = \left| {\frac{{0/8 - 1}}{1}} \right| \times 100 = 20\% \end{array}\)

الف سه عدد بین اعداد\({3^{2/5}}\) و \({3^{\sqrt {10} }}\) پیدا کنید.

ب نامعادلهٔ توانی \({4^{2a - 1}} > \frac{1}{{1024}}\) را حل کنید.

پ اگر y، x و z سه عدد حقیقی باشند، به طوری که \({a^x} > {a^y} > {a^z}\) ، آن گاه چه رابطه ای بین x و y و z برقرار است؟ (a>1)

الف

\(\sqrt {10} \simeq 3/1\quad \Rightarrow \quad {3^{2/5}}\;,\;{3^{2/6}}\;,\;{3^{2/8}}\;,\;{3^3}\;,\;{3^{\sqrt {10} }}\)

\({4^{2x - 1}} > \frac{1}{{1024}} = \frac{1}{{4{}^5}} = {4^{ - 5}} \Rightarrow 2x - 1 > - 5 \Rightarrow x > - 2\)

\(x > y > z\)

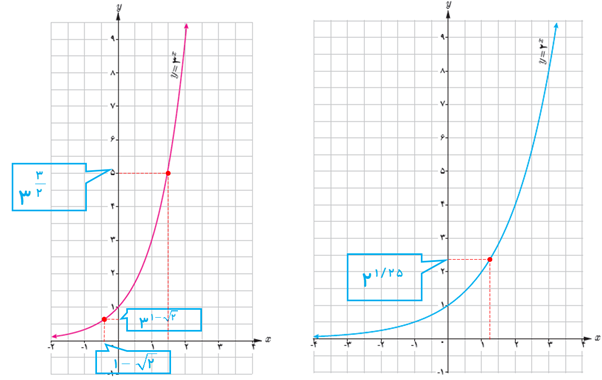
5 ابتدا مقدار تقریبی هر عدد را به کمک نمودار پیدا کنید. سپس به کمک ماشین حساب، درستی پاسخ خود را بررسی کنید.

الف \({3^{1 - \sqrt 2 }}\)

ب \({2^{1/25}}\)

پ \({3^{\frac{3}{2}}}\)

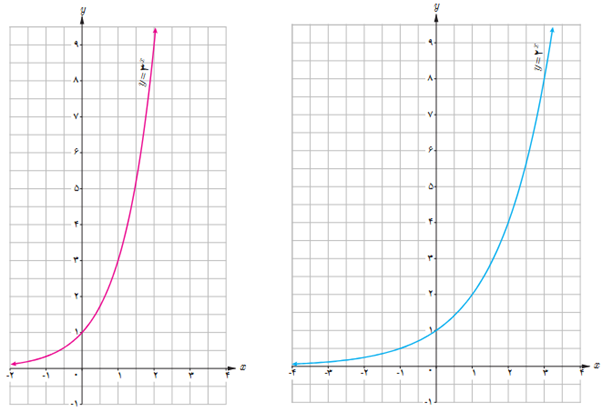
الف

\({3^{1 - \sqrt 2 }} \simeq 0/63\)

\({2^{1/25}} \simeq 2/37\)

\({3^{\frac{3}{2}}} \simeq 5/2\)

6 الف در شکل زیر خط \(y = \frac{{13}}{2}\) نمودار\(y = {2^x}\) راقطع کرده است. طول نقطه برخورد بین کدام دو عدد صحیح قرار دارد؟چرا؟

ب خط \(y = \sqrt 7 \) را رسم کنید. طول نقطه برخورد این خط و نمودار \(y = {2^x}\) بین کدام دو عدد صحیح قرار دارد؟

الف

بین دو عدد 2 و 3 ؛ زیرا : \({2^2} < \frac{{13}}{2} < {2^3}\)

بین دو عدد 1 و 2.

7 در تصفیهٔ آب، داخل فیلترها، لایهٔ تمیز کننده ای قرار دارد که حدود 30 درصد از ناخالصی ها را حذف می کند و در نتیجه 70 درصد از ناخالصی ها باقی می ماند. اگر داخل این فیلترها، دو لایه قرار دهیم، آنگاه \(0/7×0/7=0/49\) یا 49 درصد از ناخالصی ها باقی می ماند.

الف درصد ناخالصی های موجود در آب از کدام رابطه به دست می آید؟

ب با قرار دادن چند لایه در فیلتر می توان بیش از 96 درصد از ناخالصی های آب را از بین برد؟

الف

\(0/7 \to 0/7 \times 100 = 70\% \) :یک لایه

\({\left( {0/7} \right)^2} \to 0/49 \times 100 = 49\% \) :دو لایه

\({\left( {0/7} \right)^n} \to {\left( {\frac{7}{{100}}} \right)^n} \times 100 = \frac{{{7^n}}}{{{{100}^{n - 1}}}}\% \) :n لایه

\(\begin{array}{l}100\% - 96\% = 4\% \\\frac{{{7^n}}}{{{{10}^{n - 2}}}}\% < 4\% \Rightarrow \frac{{\frac{{{7^n}}}{{{{10}^{n - 2}}}}}}{{100}} = 0/04\\ \Rightarrow {\left( {0/7} \right)^n} < 0/04 \simeq {\left( {0/7} \right)^9} \Rightarrow n > 9 \Rightarrow n = 10\end{array}\)