آیا تمام سوالات فعالیت صفحه 73 حسابان یازدهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به فعالیت صفحه 73 حسابان یازدهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب فعالیت صفحه 73 درس 3 حسابان یازدهم (توابع نمایی و لگاریتمی)

تعداد بازدید : 78.86M

پاسخ فعالیت صفحه 73 حسابان یازدهم

گام به گام فعالیت صفحه 73 درس توابع نمایی و لگاریتمی

فعالیت صفحه 73 درس 3

شما در حال مشاهده جواب فعالیت صفحه 73 حسابان یازدهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

در نمودار فعالیت قبل، طول نقاط مشخص شده اعداد صحیح نامنفی هستند. می توان نقاطی از آن نمودار، با طول اعداد گویا را نیز به دست آورد.

الف جاهای خالی جدول را با قرار دادن اعداد مناسب پر کنید.

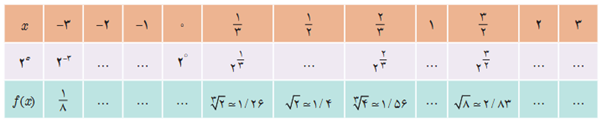
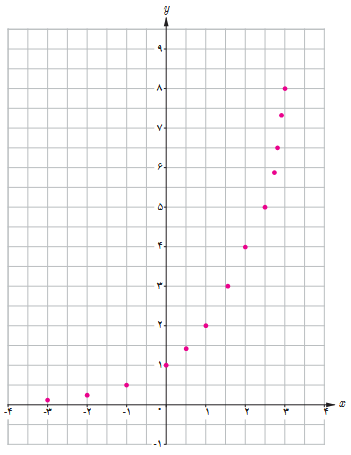
ب نقاط به دست آمده را در یک صفحهٔ شطرنجی مشخص کنید (برخی از نقاط در دستگاه مشخص شده اند).

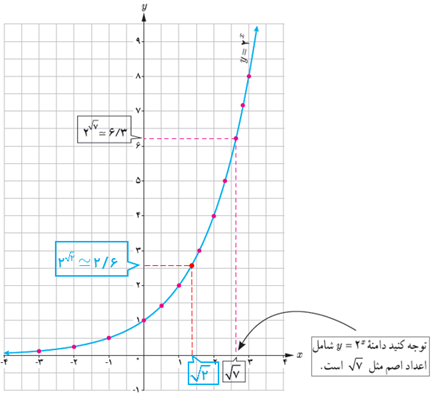
همان طور که ملاحظه می شود دامنهٔ تابع \(y = {2^x}\) همهٔ اعداد حقیقی و برد آن همواره اعداد مثبت است.

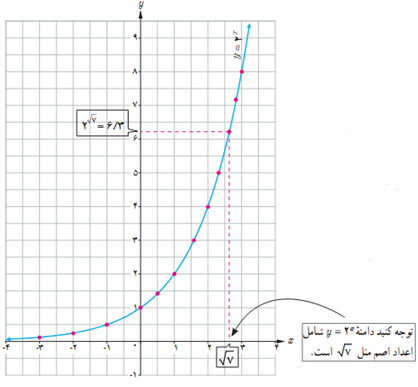
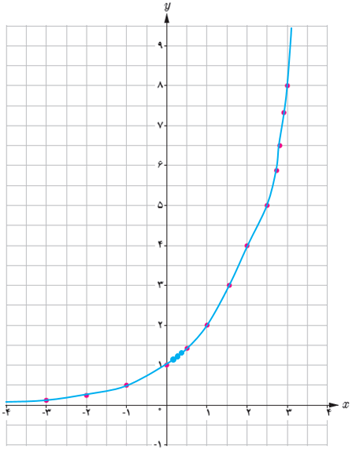
اگر تعداد نقاط خیلی زیاد شوند، شکلی شبیه نمودار روبه رو حاصل می شود.

پ چرا نمودار روبه رو یک تابع است؟

ت نقطۀ \(x = \sqrt 2 \) را روی محور xها مشخص کنید، سپس مقدار تقریبی \({2^{\sqrt 2 }}\) را با استفاده از نمودار پیدا کنید.

ث کدام یک از اعداد زیر، بین دو عدد 2³ و 2² قرار دارد؟

\(\begin{array}{l}{2^{\frac{5}{2}}}\;\;\;\;\;{2^{\frac{3}{2}}}\\\\{2^5}\;\;\;\;\;{2^{ - 1}}\end{array}\)

ج چرا نمودار تابع \(y = {2^x}\) محور xها را قطع نمی کند؟

الف

اگر خطی موازی محور y رسم کنیم، نمودار را حداکثر در یک نقطه قطع می کند.

\({2^{\frac{5}{2}}}\)

چرا که هر چه به سمت چپ محور x برویم، نمودار فقط به این محور نزدیک می شود. همچنین هنگامی تابع \(y = {2^x}\) به صفر می رسد که توان عدد 2 ، منفی بینهایت (\( - \;\infty \)) باشد.