جواب تمرین صفحه 85 درس 3 حسابان یازدهم (توابع نمایی و لگاریتمی)
تعداد بازدید : 84.81Mپاسخ تمرین صفحه 85 حسابان یازدهم
-گام به گام تمرین صفحه 85 درس توابع نمایی و لگاریتمی
-تمرین صفحه 85 درس 3
-شما در حال مشاهده جواب تمرین صفحه 85 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1- با استفاده از تعریف لگاریتم، حاصل عبارت های زیر را بیابید:
\({\log _{10}}0/01\;\;,\;\;{\log _6}\frac{1}{6}\;\;,\;\;{\log _2}\sqrt 2 \;\;,\;\;{\log _7}\sqrt[3]{{{7^2}}}\)
\(\begin{array}{l}{\log _{10}}0/01 = - 2\\\\{\log _6}\frac{1}{6} = - 1\\\\{\log _2}\sqrt 2 = \frac{1}{2}\\\\{\log _7}\sqrt[3]{{{7^2}}} = \frac{2}{3}\end{array}\)
2 نمودار تابع \(y = {\log _a}x\) را برای دو حالت \(a>1\) و \(0<a<1\) با هم مقایسه کنید.
- دامنه هر دو تابع مجموعه اعداد حقیقی مثبت و برد آنها مجموعه اعداد حقیقی است.
- در حالت 1< a ، شکل نمودار تابع به صورت افزایشی و در حالت 1> a >0، شکل نمودار به صورت کاهشی است.
- هر دو تابع از نقطه (1، 0) عبور می کنند.
3
الف خط y=27 نمودار تابع \(y = {3^x}\) را در چه نقطه ای قطع می کند؟
ب خط y=10 نمودار تابع \(y = {\left( {0/01} \right)^x}\) را در چه نقطه ای قطع می کند؟
الف
\(\left\{ \begin{array}{l}y = 27\\y = {3^x}\end{array} \right. \Rightarrow {3^x} = 27 = {3^3} \Rightarrow x = 3 \Rightarrow A\left| \begin{array}{l}3\\27\end{array} \right.\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}y = 10\\y = {\left( {0/01} \right)^x}\end{array} \right. \Rightarrow {\left( {0/01} \right)^x} = 10 \Rightarrow {\left( {{{10}^{ - 2}}} \right)^x} = 10\\ \Rightarrow - 2x = 1 \Rightarrow x = - \frac{1}{2} \Rightarrow B\left| \begin{array}{l} - \frac{1}{2}\\10\end{array} \right.\end{array}\)
4 نمودار دو تابع \(g\left( x \right) = {2^x}\;,\;f\left( x \right) = {x^2}\) را رسم کنید و سپس آنها را با هم مقایسه کنید.
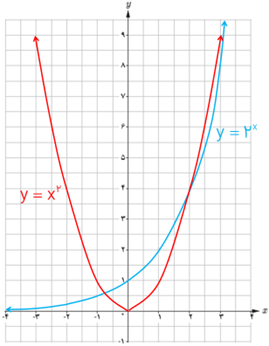
تابع \(y = {2^x}\) همواره افزایشی و یک به یک است در حالی که تابع \(y = {x^2}\) یک به یک نیست. این دو نمودار یکدیگر را در سه نقطه قطع می کنند. دو نقطه آن به طول های 4=x و 2=x و طول نقطه سوم بین دو طول 0 و 1- قرار دارد.
5 عبارت درست را با ✔ و عبارت غلط را با × علامت بزنید.
- لگاریتم اعداد مثبت کمتر از 1 همواره عددی منفی است.
- لگاریتم اعداد منفی تعریف نمی شود.
- تابع لگاریتم، تابعی یک به یک است.
- تابع لگاریتم محور yها را قطع می کند.
- اگر نقطۀ (b,d) روی نمودار \(y = {a^x}\) قرار داشته باشد، آنگاه (b,d) روی نمودار \(y = {\log _a}x\) قرار دارد.
- اگر \(a>b>0\) آنگاه \({\log _{10}}a > {\log _{10}}b\)
- لگاریتم اعداد مثبت کمتر از 1 همواره عددی منفی است. ×
- لگاریتم اعداد منفی تعریف نمی شود. ✔
- تابع لگاریتم، تابعی یک به یک است. ✔
- تابع لگاریتم محور yها را قطع می کند. ×
- اگر نقطۀ (b,d) روی نمودار \(y = {a^x}\) قرار داشته باشد، آنگاه (b,d) روی نمودار \(y = {\log _a}x\) قرار دارد. ✔
- اگر \(a>b>0\) آنگاه \({\log _{10}}a > {\log _{10}}b\) ×
6 نمودار تابع های زیر را رسم کنید.
الف \(y = 1 + {\log _3}x\)
ب \(y = - {3^x} - 2\)
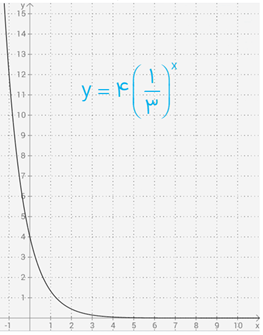
پ \(y = 4{\left( {\frac{1}{3}} \right)^x}\)
الف
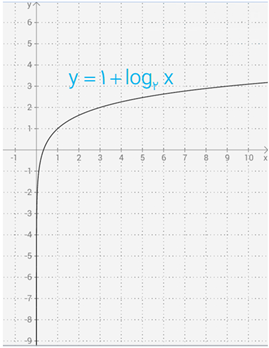
ب
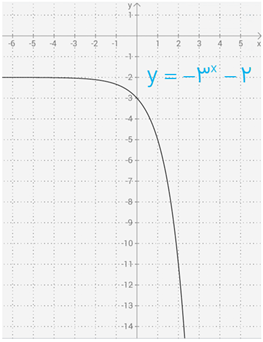
پ
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















