جواب تمرین صفحه 125 درس 5 حسابان دوازدهم (کاربردهای مشتق)
تعداد بازدید : 84.8Mپاسخ تمرین صفحه 125 حسابان دوازدهم
-گام به گام تمرین صفحه 125 درس کاربردهای مشتق
-تمرین صفحه 125 درس 5
-شما در حال مشاهده جواب تمرین صفحه 125 حسابان دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
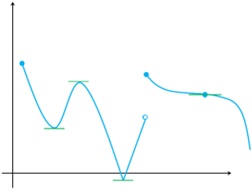
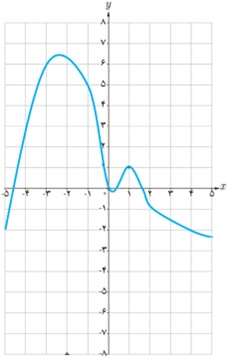
1 نمودار تابعی را رسم کنید که همهٔ شرایط زیر را داشته باشد.
نقطهٔ ماکزیمم نسبی داشته باشد که مشتق در آن برابر صفر باشد.
نقطهٔ مینیمم نسبی داشته باشد که تابع در آن نقطه پیوسته باشد ولی مشتق نداشته باشد.
نقطهٔ ماکزیمم نسبی داشته باشد که تابع در آن ناپیوسته باشد.
نقطه ای داشته باشد که اکسترمم نسبی نباشد ولی مشتق تابع در آن نقطه صفر باشد.
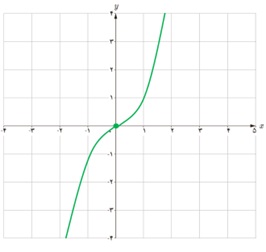
2 نمودار تابعی را رسم کنید که بر دامنه اش پیوسته باشد ولی بر آن ماکزیمم و مینیمم مطلق نداشته باشد.
3 برای هر مورد زیر نمودار یک تابع را رسم کنید.
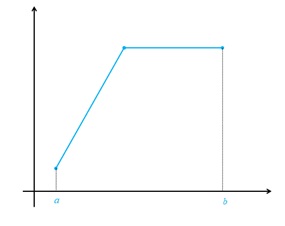
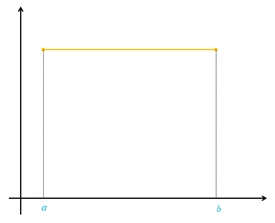
الف تابع f در بازه ای مانند [a,b] صعودی است اما صعودی اکید نیست.
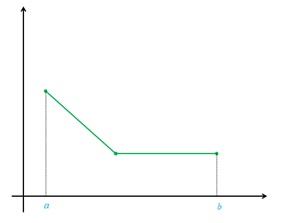
ب تابع f در بازه ای مانند [a,b] نزولی است اما نزولی اکید نیست.
پ تابع f در بازه ای مانند [a,b] هم صعودی و هم نزولی است.
الف
ب
پ
4 برای هر کدام از موارد زیر نمودار یک تابع را رسم کنید.
الف تابعی که در یک بازه اکیداً نزولی است اما در برخی نقاط آن بازه پیوسته نیست.
ب تابعی که در یک بازه اکیداً صعودی و بر آن بازه پیوسته است اما در برخی نقاط آن بازه مشتق پذیر نیست.
پ تابعی که در یک بازه اکیداً نزولی و مشتق پذیر است اما مشتق آن در برخی نقاط منفی نباشد.
الف
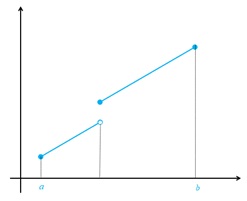
ب
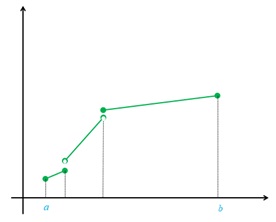
پ
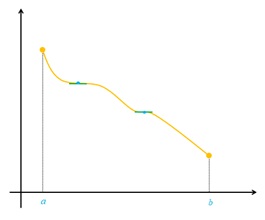
5 نمودار تابع f را به گونه ای رسم کنید که ماکزیمم مطلق داشته باشد ولی تابع |f| ماکزیمم مطلق نداشته باشد.
6 نقاط اکسترمم نسبی و مطلق توابع زیر را در بازه های داده شده در صورت وجود بیابید.
الف \(f\left( x \right) = 3{x^2} - 2x + 5\;\;\;\;\left[ { - 2,1} \right]\)
ب \(f\left( x \right) = {x^3} - 3x\;\;\;\;\left[ { - 1,2} \right]\)
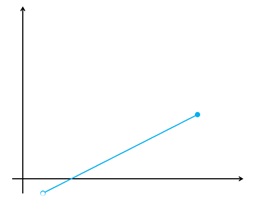
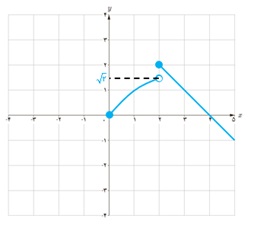
پ \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt x \;\;\;\;\;\;0 \le x < 2\\\\4 - x\;\;\;\;\;x \ge 2\end{array} \right.\)
الف
\(\begin{array}{l}f'(x) = 6x - 2 \Rightarrow 6x - 2 = 0 \Rightarrow x = \frac{1}{3}\\\left\{ \begin{array}{l}x = - 2 \Rightarrow y = 12 + 4 + 5 = 21\\x = \frac{1}{3} \Rightarrow y = \frac{1}{3} - \frac{2}{3} + 5 = \frac{{14}}{3}\\x = 1 \Rightarrow y = 3 - 2 + 5 = 6\end{array} \right.\end{array}\)
\(21 \to \max \)اکسترمم مطلق
اکسترمم مطلق\(\frac{{14}}{3} \to \min \)
ب
\(\begin{array}{l}f'(x) = 3{x^2} - 3 \Rightarrow 3{x^2} - 3 = 0 \Rightarrow x = \pm 1\\\left\{ \begin{array}{l}x = - 1 \Rightarrow y = - 1 + 3 = 2\\x = 1 \Rightarrow y = 1 - 3 = - 2\\x = 2 \Rightarrow y = 8 - 6 = 2\end{array} \right.\end{array}\)
اکسترمم مطلق\(2 \to \max \)
\( - 2 \to \min \) اکسترمم مطلق
اکسترمم مطلق\(2 \to \max \)
پ
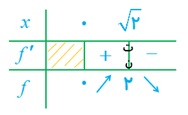
\(f'(x) = \left\{ \begin{array}{l}\frac{1}{{2\sqrt x }}\quad \quad 0 < x < 2\\ - 1\quad \quad \quad \;\;x > 2\end{array} \right.\)
7 ضرایب a و b را در تابع 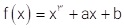 طوری پیدا کنید که در نقطه (1,2)، مینیمم نسبی داشته باشد.
طوری پیدا کنید که در نقطه (1,2)، مینیمم نسبی داشته باشد.
\(\begin{array}{l}\left( {1\;,\;2} \right) \Rightarrow 1 + a + b = 2 \Rightarrow a + b = 1\quad \left( i \right)\\f'(x) = 3{x^2} + a \Rightarrow f'(1) = 0 \Rightarrow 3 + a = 0 \Rightarrow a = - 3\\\left( i \right):\quad \Rightarrow - 3 + b = 1 \Rightarrow b = 4\end{array}\)
8 نمودار تابعی مانند f را به گونه ای رسم کنید که در تمام شرایط زیر صدق کند.
f(-1) = 5 , f(4) = -2 , f(0) = 0
نقطه (1,1) ماکزیمم نسبی این تابع باشد.
9 یک برگه کاغذی مستطیل شکل با اضلاع x و y در اختیار داریم. با بریدن چهار مربع به ضلع h از گوشه های آن و تا زدن اضلاع، یک مکعب ساخته شده است. اگر xy=100cm2 و h=2cm مقادیر x و y را طوری پیدا کنید که حجم این مکعب بیشترین مقدار ممکن شود.
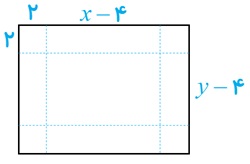
\(\begin{array}{l}x\;y = 100 \Rightarrow y = \frac{{100}}{x}\\V = 2(x - 4)(y - 4) = 2xy - 8x - 8y + 32\\V(x) = 232 - 8x - \frac{{800}}{x} = \frac{{232x - 8{x^2} - 800}}{x}\\ \Rightarrow V'(x) = \frac{{(232 - 16x)x - 1(232x - 8{x^2} - 800)}}{{{x^2}}}\\ \Rightarrow V'(x) = \frac{{ - 8{x^2} + 800}}{{{x^2}}} = 0 \Rightarrow - 8{x^2} + 800 \Rightarrow {x^2} = 100\\ \Rightarrow x = 10\\ \Rightarrow y = 10\end{array}\)
10 یک مستطیل در یک نیم دایره محاط شده است. اگر شعاع دایره، 4 سانتی متر باشد، طول و عرض مستطیل را طوری به دست آورید که مساحت آن بیشترین مقدار ممکن باشد.
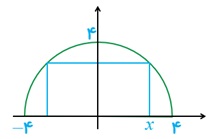
\(\begin{array}{l}y = \sqrt {16 - {x^2}} \\S = 2x.y = 2x\sqrt {16 - {x^2}} \\S'(x) = 2\sqrt {16 - {x^2}} + \frac{{2x( - 2x)}}{{2\sqrt {16 - {x^2}} }} = \frac{{2(16 - {x^2}) - 2{x^2}}}{{\sqrt {16 - {x^2}} }}\\S'(x) = \frac{{32 - 4{x^2}}}{{\sqrt {16 - {x^2}} }} = 0 \Rightarrow 4{x^2} = 32 \Rightarrow {x^2} = 8 \Rightarrow x = \sqrt 8 \\ \Rightarrow y = \sqrt 8 \end{array}\)
11 توابع زیر در چه بازه هایی صعودی و در چه بازه هایی نزولی اند؟
الف \(f\left( x \right) = 4{x^3} - 3{x^2} - 12x + 7\)
ب \(f\left( x \right) = \frac{x}{{x - 2}}\)
الف
\(\begin{array}{l}f(x) = 2{x^3} - 3{x^2} - 12x + 7\\f'(x) = 6{x^2} - 6x - 12 = 0 \Rightarrow {x^2} - x - 2 = 0 \Rightarrow (x - 2)(x + 1) = 0 \Rightarrow \left\{ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\end{array}\)
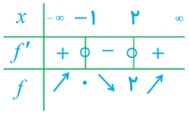
در بازه های 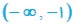 و
و  صعودی و در بازه ی (-1,2) نزولی.
صعودی و در بازه ی (-1,2) نزولی.
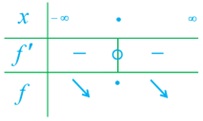
ب
\(\begin{array}{l}f(x) = \frac{x}{{x - 2}}\\f'(x) = \frac{{1(x - 2) - 1(x)}}{{{{(x - 2)}^2}}} = \frac{{ - 2}}{{{{(x - 2)}^2}}} < 0\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















