جواب تمرین صفحه 117 درس 7 ریاضی نهم (عبارت های گویا)
تعداد بازدید : 80.83Mپاسخ تمرین صفحه 117 ریاضی نهم
-گام به گام تمرین صفحه 117 درس عبارت های گویا
-تمرین صفحه 117 درس 7
-شما در حال مشاهده جواب تمرین صفحه 117 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 برای هر عبارت گویا، مقادیری را به دست آورید که عبارت به ازای آنها تعریف نشده است.
\(\frac{{5x}}{{3a{b^2}}}\) الف
\(\frac{{2y}}{{y\left( {2y - 6} \right)}}\) ب
\(\frac{{2P}}{{{P^2} - P - 12}}\) ج
\(\frac{{2x + 5}}{x}\) د
\(\frac{{{x^2} - 1}}{{x + 5}}\) هـ
\(\frac{{5x}}{{3a{b^2}}} \Rightarrow 3a{b^2} = 0 \Rightarrow \left\{ \begin{array}{l}a = 0\\\\{b^2} = 0 \Rightarrow b = 0\end{array} \right.\) الف
\(\frac{{2y}}{{y\left( {2y - 6} \right)}} \Rightarrow y\left( {2y - 6} \right) = 0\) ب
\( \Rightarrow \left\{ \begin{array}{l}y = 0\\\\2y - 6 = 0 \Rightarrow y = 3\end{array} \right.\)
\(\frac{{2P}}{{{P^2} - P - 12}} \Rightarrow {P^2} - P - 12 = 0\) ج
\(\begin{array}{l} \Rightarrow (P - 4)(P + 3) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}P - 4 = 0 \Rightarrow P = 4\\\\P + 3 = 0 \Rightarrow P = - 3\end{array} \right.\end{array}\)
\(\frac{{2x + 5}}{x} \Rightarrow x = 0\) د
\(\frac{{{x^2} - 1}}{{x + 5}} \Rightarrow x + 5 = 0 \Rightarrow x = - 5\) هـ

برای حل این مسئله کافی است که مخرج را برابر با صفر قرار دهیم تا جواب های مسئله بدست بیاید.
2 حاصل هر عبارت را به ساده ترین صورت بنویسید:
\(\frac{{3 - x}}{{{x^2} - 5x + 6}}\) الف
\(\frac{{4{x^2} + 8x}}{{12x + 24}}\) ب
\(\frac{{24{x^2}}}{{12{x^2} - 6x}}\) ج
\(\frac{{{y^3} - 2{y^2} - 3y}}{{{y^2} + y}}\) د
\(\frac{{1 - {t^4}}}{{{t^2} + 1}}\) هـ
\(\frac{{6{a^4}{b^2}}}{{4a{b^8}}}\) و
\(\frac{{3 - x}}{{{x^2} - 5x + 6}} = \frac{{ - (x - 3)}}{{(x - 3)(x - 2)}} = \) الف
\(\frac{{ - 1}}{{x - 2}}\)
برای ساده کردن این قسمت، از صورت یک علامت منفی فاکتور می گیریم و مخرج را به کمک اتحاد جمله مشترک تجزیه می کنیم؛ سپس جمله های مشترک در صورت و مخرج را خط می زنیم.
\(\frac{{4{x^2} + 8x}}{{12x + 24}} = \frac{{4x(x + 2)}}{{12(x + 2)}} = \frac{{4x}}{{12}} = \frac{x}{3}\) ب
برای ساده کردن این قسمت، از صورت از عبارت 4x فاکتور می گیریم، همچنین از مخرج از عدد 12 فاکتور می گیریم و سپس عامل های مشترک را حذف می کنیم.
\(\frac{{24{x^2}}}{{12{x^2} - 6x}} = \frac{{6x \times 4x}}{{6x(2x - 1)}} = \frac{{4x}}{{2x - 1}}\) ج
برای ساده کردن این قسمت، از صورت از عبارت 6x فاکتور می گیریم و از مخرج نیز از همین عبارت فاکتور می گیریم، سپس این عامل را خط می زنیم.
\(\frac{{{y^3} - 2{y^2} - 3y}}{{{y^2} + y}} = \frac{{y({y^2} - 2y - 3)}}{{y(y + 1)}} = \) د
\(\begin{array}{l}\frac{{{y^2} - 2y - 3}}{{y + 1}} = \frac{{(y + 1)(y - 3)}}{{y + 1}} = \\\\y - 3\end{array}\)
برای ساده کردن این قسمت، ابتدا از صورت و از مخرج، جمله y را فاکتور می گیریم؛ سپس آن را از صورت و مخرج خط می زنیم. سپس صورت را با کمک اتحاد جمله مشترک تجزیه کرده و جمله های y+1 را از صورت و مخرج خط می زنیم.
\(\frac{{1 - {t^4}}}{{{t^2} + 1}} = \frac{{(1 - {t^2})(1 + {t^2})}}{{{t^2} + 1}} = (1 - {t^2})\) هـ
برای ساده کردن این قسمت، مخرج را به کمک اتحاد مزدوج تجزیه می کنیم و سپس عامل مشترک را از صورت و مخرج خط می زنیم.
\(\frac{{6{a^4}{b^2}}}{{4a{b^8}}} = \frac{{2a{b^2} \times 3{a^3}}}{{2 \times 2a{b^2}}} = \frac{3}{2}{a^3}\) و
برای ساده کردن این قسمت نیز به کمک فاکتورگیری از صورت و مخرج، عبارت \(2a{b^2}\) را حذف می کنیم.
3 عبارت هایی را که حاصل آنها 1 و یا 1- است، معلوم کنید.
\(\frac{{2y + 3}}{{2y - 3}}\) الف
\(\frac{{2y - 3}}{{3 - 2y}}\) ب
\(\frac{{2y + 3}}{{3 + 2y}}\) ج
\(\frac{{2y + 3}}{{ - 2y - 3}}\) د
\(\frac{{2y + 3}}{{2y - 3}}\) الف
این عبارت قابل ساده شدن نیست.
\(\frac{{2y - 3}}{{3 - 2y}} = \frac{{2y - 3}}{{ - (2y - 3)}} = \frac{1}{{ - 1}} = - 1\) ب
اگر از مخرج، علامت منفی را فاکتور بگیریم؛ بعد از ساده کردن عبارت مذکور -1 می شود.
\(\frac{{2y + 3}}{{3 + 2y}} = \frac{{2y + 3}}{{2y + 3}} = 1\) ج
پس از ساده سازی، این عبارت گویا برابر با 1 می شود.
\(\frac{{2y + 3}}{{ - 2y - 3}} = \frac{{2y + 3}}{{ - (2y + 3)}} = \frac{1}{{ - 1}} = - 1\) د
اگر از مخرج، علامت منفی را فاکتور بگیریم؛ بعد از ساده کردن عبارت مذکور -1 می شود.
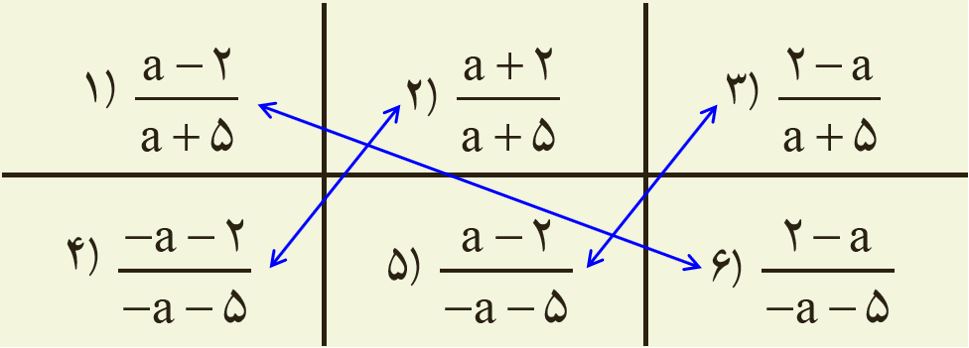
4 هر یک از عبارت های داده شده در سطر اول را به عبارت مساوی آن در سطر دوم وصل کنید.
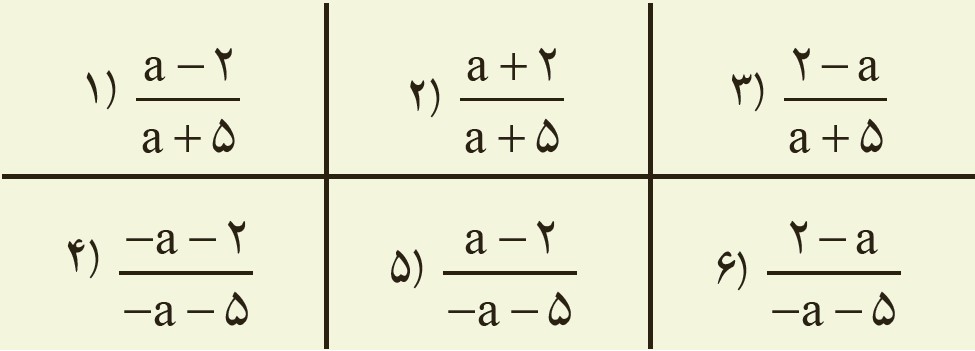
5 از عبارت های زیر، هر کدام را که با عبارت \(\frac{{z(x + y)}}{t}\) برابر است، مشخص کنید.
\(\frac{z}{t}\left( {x + y} \right)\) الف
\(\frac{{zx + y}}{t}\) ب
\(\frac{1}{t} \times z\left( {x + y} \right)\) ج
\(z \times \frac{{x + y}}{t}\) د
\(\frac{{zx}}{t} + \frac{{zy}}{t}\) هـ
\(\frac{{zx}}{t} + y\) و
الف برابر هست
ب برابر نیست
ج برابر هست
د برابر هست
هـ برابر هست
و برابر نیست
6 در جای خالی چه عبارتی باید نوشت؟
\(\frac{{1 - z}}{z} = \frac{{}}{{z\left( {{z^2} + 1} \right)}}\) الف
\(\frac{{3x}}{{x - 3}} = \frac{{}}{{{x^2} - x - 6}}\) ب
\(\frac{{3y + 2}}{5} = \frac{1}{5}\left( {\;\;\;\;\;\;\;\;\;} \right)\) ج
\(\frac{{\left( {x - 5} \right)\left( {\;\;\;\;\;\;} \right)}}{{\left( {x - 2} \right)\left( {x - 5} \right)}} = x + 1\) د
\(\frac{{1 - z}}{z} = \frac{{}}{{z\left( {{z^2} + 1} \right)}}\) الف
\(\begin{array}{l} \Rightarrow \frac{{1 - z}}{z} = \frac{{1 - z}}{z} \times \frac{{{z^2} + 1}}{{{z^2} + 1}} = \\\\\frac{{(1 - z)({z^2} + 1)}}{{z({z^2} + 1)}}\\\\ \Rightarrow \frac{{1 - z}}{z} = \frac{{(1 - z)({z^2} + 1)}}{{z\left( {{z^2} + 1} \right)}}\end{array}\)
در جای خالی بایستی عبارت \({z^2} + 1\) نوشته شود.
\(\frac{{3x}}{{x - 3}} = \frac{{}}{{{x^2} - x - 6}}\) ب
\(\begin{array}{l} \Rightarrow {x^2} - x - 6 = (x - 3)(x + 2)\\\\ \Rightarrow \frac{{3x}}{{x - 3}} = \frac{{}}{{(x - 3)(x + 2)}}\\\\ \Rightarrow \frac{{3x}}{{x - 3}} = \frac{{3x}}{{x - 3}} \times \frac{{x + 2}}{{x + 2}} = \\\\\frac{{3x(x + 2)}}{{(x - 3)(x + 2)}} = \frac{{3{x^2} + 6x}}{{{x^2} - x - 6}}\\\\ \Rightarrow \frac{{3x}}{{x - 3}} = \frac{{3{x^2} + 6x}}{{{x^2} - x - 6}}\end{array}\)
در جای خالی بایستی عبارت \(3{x^2} + 6x\) نوشته شود.
\(\frac{{3y + 2}}{5} = \frac{1}{5}\left( {\;\;\;\;\;\;\;\;\;} \right)\) ج
\(\begin{array}{l} \Rightarrow \frac{{3y + 2}}{5} = \frac{{1 \times (3y + 2)}}{5} = \frac{1}{5}\left( {3y + 2} \right)\\\\ \Rightarrow \frac{{3y + 2}}{5} = \frac{1}{5}\left( {3y + 2} \right)\end{array}\)
در جای خالی بایستی عبارت \(3y + 2\) نوشته شود.
\(\frac{{\left( {x - 5} \right)\left( {\;\;\;\;\;\;} \right)}}{{\left( {x - 2} \right)\left( {x - 5} \right)}} = x + 1\) د
\(\begin{array}{l} \Rightarrow (x + 1) \times \frac{{x - 2}}{{x - 2}} \times \frac{{x - 5}}{{x - 5}} = \\\\\frac{{(x + 1)(x - 2)(x - 5)}}{{(x - 2)(x - 5)}} = \\\\\frac{{(x - 5)\left( {(x + 1)(x - 2)} \right)}}{{(x - 2)(x - 5)}} = \\\\\frac{{(x - 5)({x^2} - x - 2)}}{{(x - 2)(x - 5)}}\\\\ \Rightarrow \frac{{(x - 5)({x^2} - x - 2)}}{{(x - 2)(x - 5)}} = x + 1\end{array}\)
در جای خالی بایستی عبارت \({x^2} - x - 2\) نوشته شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















