گام به گام کار در کلاس صفحه 117 درس 7 ریاضی نهم (عبارت های گویا)

انواع روش های تجزیه عبارت های کویا:

1 فاکتور گیری (خارج کردن عامل مشترک):

در این روش، عوامل مشترک بین جمله‌ها را شناسایی و آن‌ها را خارج می‌کنیم؛ به عنوان مثال در قسمت (ب) با استفاده از فاکتورگیری، عامل مشترک را خارج می کنیم:

\(\frac{{6m + 18}}{{7m + 21}} = \frac{{6(m + 3)}}{{7(m + 3)}} = \frac{6}{7}\)

2 تجزیه به کمک اتحادها:

عبارت های گویا به کمک اتحادها و روابط بین آن ها تجزیه می کنیم. انواع اتحادها را در زیر آورده ایم:

الف اتحاد مربع دوجمله‌ای:

\(\begin{array}{l}{(a + b)^2} = {a^2} + 2ab + {b^2}\\\\{(a - b)^2} = {a^2} - 2ab + {b^2}\end{array}\)

ب اتحاد مزدوج:

\((a + b)(a - b) = {a^2} - {b^2}\)

پ اتحاد مکعب دوجمله ای:

\(\begin{array}{l}{(a + b)^3} = {a^3} + 2{a^2}b + 2a{b^2} + {b^3}\\\\{(a - b)^3} = {a^3} - 2{a^2}b + 2a{b^2} + {b^3}\end{array}\)

ت مجموع و تفاضل مکعب ها:

این اتحاد به اتحاد »چاق و لاغر» هم معروف می باشد:

\(\begin{array}{l}{a^3} + {b^3} = (a + b)({a^2} - ab + {b^2})\\\\{a^3} - {b^3} = (a - b)({a^2} + ab + {b^2})\end{array}\)

ث اتحاد جمله مشترک:

\((x + a)(x + b) = {x^2} + (a + b)x + ab\)

ج اتحاد مربع سه جمله‌ای:

\(\begin{array}{l}{(a + b + c)^2} = \\\\{a^2} + {b^2} + {c^2} + 2ab + 2ac + 2bc\end{array}\)

برای قسمت های (الف) و (د) مسئله 1، برای تجزیه صورت از اتحاد مزدوج و برای تجزیه مخرج با استفاده از روش فاکتور گیری استفاده شده است.

3 تجزیه به کمک اتحاد جمله مشترک:

هر چند که در قسمت اتحادها به این قسمت اشاره ای کوچک شد، اما این اتحاد جزو پرکاربردترین اتحادها هست که از آن برای تجزیه اتحادهای چند جمله ای درجۀ دوم استفاده می شود و کاربرد زیادی نیز در حل معادلات درجه دوم که در سال های بعد می خوانید، دارد. بنابراین در این قسمت به صورت ویژه به آن می پردازیم.

فرم اتحاد جمله مشترک به صورت زیر می باشد:

\((x + a)(x + b) = {x^2} + (a + b)x + ab\)

بیایید با بیان مثال، این اتحاد را بیشتر توضیح دهیم.

مثال:

می خواهیم که چندجمله ای درجه دوم زیر را به صورت ضرب دو عبارت یک جمله ای تجزیه کنیم:

\({x^2} + 5x + 6 = \)

حاصل این چند جمله ای به این صورت می شود:

\({x^2} + 5x + 6 = (x + ...)\,\,(x + ...)\)

در جای خالی چه اعدادی بگذاریم که ضریب x آن عدد 5 و عدد ثابت آن عدد 6 شود؟

بیایید فرض کنیم که دو عدد را پیدا کرده ایم و یکی α و دیگری β باشد. یعنی بدین صورت:

\({x^2} + 5x + 6 = (x + \alpha )\,\,(x + \beta )\)

در این صورت پس از ساده سازی خواهیم داشت:

\({x^2} + 5x + 6 = {x^2} + (\alpha + \beta )x + \alpha \beta \)

پس α و β باید مقدارهایی داشته باشند که اگر آن ها را پیدا کردیم، ضرب این دو عدد بایستی +6 و جمع این دو عدد بایستی +5 شود. «ترتیب گفتاری اینجا مهم هست!» حتما دقت کنید که علامت هایشان را هم می نویسیم.

می توانیم به این صورت عمل کنیم:

«دو عدد پیدا کنید که ضرب آن ها برابر با +6 و جمع آن ها برابر با +5 شود.»

برای حل این مسئله از آزمون و خطا می رویم:

ضرب دو عدد را با × و جمع دو عدد را با + نشان می دهیم و ستون زیر را می کشیم:

حتما دقت کنید که ضرب و جمع در سمت چپ ستون و اول ضرب نوشته شود و سپس در زیر آن جمع!

همچنین در سمت راست ستون از عدد 1 تا عدد ضرب که همان 6 هست در زیر هم می نویسیم.

عدد ضرب را در جلوی اعداد سمت راست می نویسیم:

حالا برای ردیف اول اعداد سمت راست، عدد 6 را تقسیم بر عدد 1 می کنیم و حاصل را بدست می آوریم:

حاصل عدد 7 بدست آمد. این عدد را با عدد +5 که جمع دو عدد می باشد مقایسه می کنیم. با هم برابر نیستند. پس سراغ ردیف بعدی می رویم.

در ردیف دوم سمت راست، عدد 6 را تقسیم بر عدد 2 می کنیم و حاصل را بدست می آوریم:

حاصل عدد 5 بدست آمد. این عدد با عدد جمع برابر است. بنابراین دو عدد پیدا شدند. آن دو عدد 2 و 3 می باشد؛ چرا که ضرب آن دو برابر 6 و جمع آن دو برابر با 5 می شود.

بنابراین در جاهای خالی اعداد 2 و 3 را قرار می دهیم:

\({x^2} + 5x + 6 = (x + 2)\,\,(x + 3)\)

مثال دیگری برای این نوع تجزیه می زنیم. می خواهیم عبارت زیر را تجزیه کنیم:

\({x^2} + 2x - 15 = \)

بیایید فرض کنیم که دو عدد را پیدا کرده ایم و یکی α و دیگری β باشد. یعنی بدین صورت:

\({x^2} + 2x - 15 = (x + \alpha )\,\,(x + \beta )\)

در این صورت پس از ساده سازی خواهیم داشت:

\({x^2} + 2x - 15 = {x^2} + (\alpha + \beta )x + \alpha \beta \)

پس α و β باید مقدارهایی داشته باشند که اگر آن ها را پیدا کردیم، ضرب این دو عدد بایستی -15 و جمع این دو عدد بایستی +2 شود. باز هم برای تأکید، «ترتیب گفتاری اینجا مهم هست!» حتما دقت کنید که علامت هایشان را هم می نویسیم.

می توانیم به این صورت عمل کنیم:

«دو عدد پیدا کنید که ضرب آن ها برابر با -15 و جمع آن ها برابر با +2 شود.»

برای حل این مسئله از آزمون و خطا می رویم:

ضرب دو عدد را با × و جمع دو عدد را با + نشان می دهیم و ستون زیر را می کشیم:

در این جا این بار به این علت که تعداد اعداد زیاد می شوند، ستون اعداد را تا 6 نوشتیم، چون می دانیم که تا قبل از عدد 6 به جواب خواهیم رسید (در غیر این صورت تا عدد 15 می نویسیم!)

حال در مقابل هر عدد، آن عددی که حاصل ضرب دو عدد هست یعنی -15 را می نویسیم:

حال از ردیف اول شروع می کنیم و 15 را بر عدد 1 تقسیم می کنیم و حاصل را بدست می آوریم:

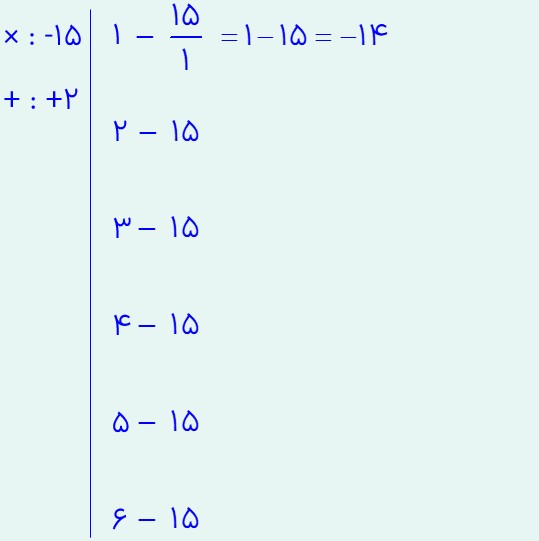
حاصل عدد -14 بدست آمد. این عدد را با عدد +2 که جمع دو عدد می باشد مقایسه می کنیم. با هم برابر نیستند. پس سراغ ردیف بعدی می رویم. در این ردیف، عدد 15 را بر 2 تقسیم می کنیم و حاصل را بدست می آوریم:

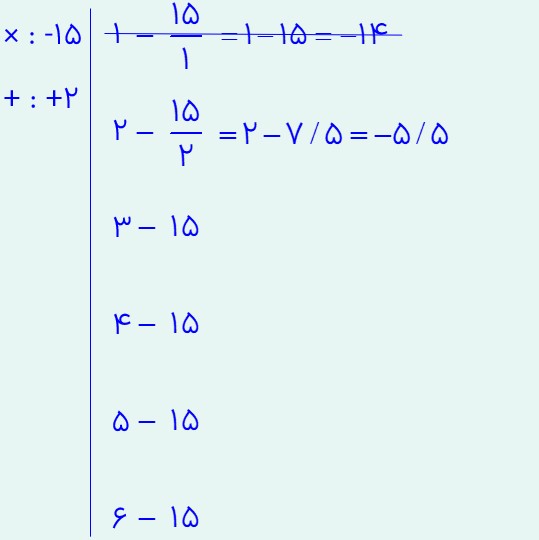
حاصل عدد اعشاری بدست آمد؛ پس جواب نمی تواند باشد. زیرا حاصل جمع یک عدد صحیح است. پس به سراغ ردیف سوم می رویم. در این ردیف، عدد 15 را بر 3 تقسیم می کنیم و حاصل را بدست می آوریم:

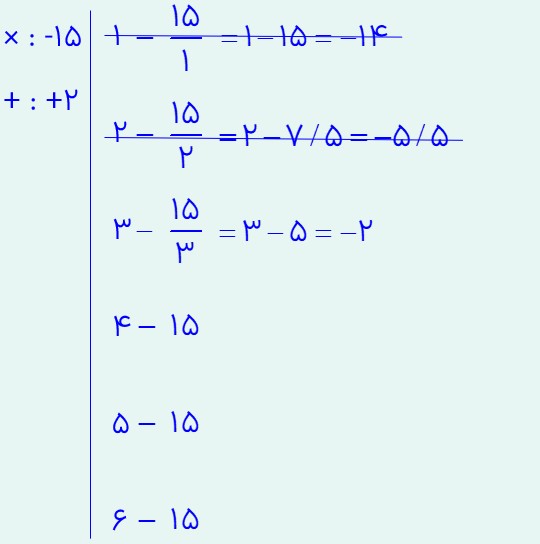
حاصل عدد -2 بدست آمد. جمع دو عدد نیست، اما قرینه آن هست. پس کافی است که دو عددی که بدست آوردیم را قرینه کنیم. یعنی اگر جمع اعداد 3 و -5 برابر -2 می شود، کافی است که این اعداد را قرینه کنیم. یعنی -3 و 5 که اگر جمع کنیم برابر با 2 بدست می آید. همچنین ضرب این دو عدد برابر با -15 می شود. پس دو عدد بدست آمد. فقط توجه کنید که اعدادی که در محاسبه بدست آوردیم، اعداد 3 و -5 می باشند که جمع آن دو برابر با -2 می شود.

به همین دلیل که عدد -2 با عدد 2 قرینه است، قرینه اعداد 3 و -5 را بدست آوردیم. در نهایت دو عدد برابر با وردیم. در نهایت دو عدد برابر با -3 و 5 شد. کافی است که این دو عدد را در جای خالی بگذاریم:

\({x^2} + 2x - 15 = (x - 3)\,\,(x + 5)\)

به این صورت چند جمله ای های درجه 2 را تجزیه می کنیم.

فقط نکته ای که بایستی آن را در نظر بگیریم این است که اگر در محاسبه ستونی که انجام می دادیم، اگر تا آخرین عدد پیش رفتیم و حاصل جمع یا تفریق برابر با عدد جمع نشد، هیچ دو عددی پیدا نمی شود که به جای α و β قرار گیرد. در نتیجه چند جمله ای درجه 2 تجزیه پذیر نمی باشد.

در مسئله ای که حل کردیم، صورت و مخرج مورد (ج) از این تجزیه استفاده شده است.