درسنامه کامل ریاضی چهارم فصل 1 اعداد و الگوها
تعداد بازدید : 7.59Mخلاصه نکات ریاضی چهارم فصل 1 اعداد و الگوها - درسنامه شب امتحان ریاضی چهارم فصل 1 اعداد و الگوها - جزوه شب امتحان ریاضی چهارم نوبت اول فصل 1 اعداد و الگوها
حل مساله - الگوهای - رسم شکل
الگویابی
یکی از روش های حل مساله، روش الگو یابی یا کشف رابطه ها است. الگو ها دو دسته هستند :
الگوهای عددی - الگوهای هندسی
الگوهای عددی
در الگوهای عددی رابطه ای افزایشی یا کاهشی بین اعداد پیدا می کنیم.
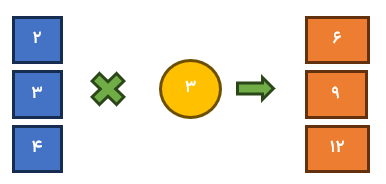
در این الگوی عددی هر عدد ۳ واحد بیشتر از عدد قبلی است.
\(6\mathop \to \limits^{ + 3} 9\mathop \to \limits^{ + 3} 12\mathop \to \limits^{ + 3} 15\)
در این الگو عددی هر عدد ۲ برابر عدد قبلی است.
\(10\mathop \to \limits^{ \times 2} 20\mathop \to \limits^{ \times 2} 40\mathop \to \limits^{ \times 2} 80\)
در این الگو بر هر درد ۲۵ واحد از عدد قبلی کمتر است.
\(175\mathop \to \limits^{ - 25} 150\mathop \to \limits^{ - 25} 125\mathop \to \limits^{ - 25} 100\)
الگوی هندسی
در الگوهای هندسی رابطه ای بین اشکال پیدا می کنیم.
در این الگوی هندسی هر شکل ۲ واحد از شکل قبلی بیشتر است.
\(2\mathop \to \limits^{ + 2} 4\mathop \to \limits^{ + 2} 6\mathop \to \limits^{ + 2} 8\)
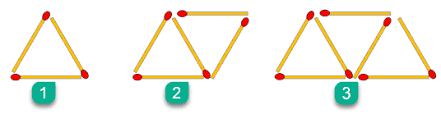
در این الگو ار هندسی هر شکل 3 چوب کبریت از شکل قبلی بیشتر دارد.
الگوهای عددی زیر را ادامه دهید.
\(1)130 - 260 - 390 - ....... - ....... - ....... - ....... - \)
\(130\mathop \to \limits^{ + 130} 260\mathop \to \limits^{ + 130} 390\mathop \to \limits^{ + 130} 520\mathop \to \limits^{ + 130} 650\mathop \to \limits^{ + 130} 780\mathop \to \limits^{ + 130} 910\)
\(2)120 - 340 - 560 - ...... - ...... - ...... - ...... - \)
\(120\mathop \to \limits^{ + 220} 340\mathop \to \limits^{ + 220} 560\mathop \to \limits^{ + 220} 780\mathop \to \limits^{ + 220} 1000\mathop \to \limits^{ + 220} 1220\mathop \to \limits^{ + 220} 1440\)
\(3)\,10 - 30 - 70 - ........ - ........ - ........ - ........ - \)
\(10\mathop \to \limits^{ + 20} 30\mathop \to \limits^{ + 40} 70\mathop \to \limits^{ + 60} 130\mathop \to \limits^{ + 80} 210\mathop \to \limits^{ + 100} 310\mathop \to \limits^{ + 120} 430\)
به الگوی زیر توجه کنید.
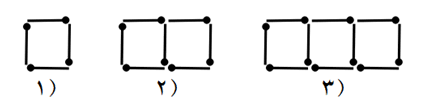
الف چه الگویی در کشیدن شکل ها وجود دارد؟
تعداد مربع ها در هر مرحله نسبت به مرحله قبل یک واحد بیشتر است (در هر مرحله 3 چوب کبریت اضافه می شود)
ب اگر الگوی هندسی به الگوی عددی تبدیل شود شکل ششم از چند چوب کبریت ساخته می شود؟
\(4\mathop \to \limits^{ + 3} 7\mathop \to \limits^{ + 3} 10\mathop \to \limits^{ + 3} 13\mathop \to \limits^{ + 3} 16\mathop \to \limits^{ + 3} 19\)
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
عدد نویسی
عدد نویسی
هر عدد از یک، دو یا چند رقم ساخته می شود و ارزش هر رقم در یک عدد بستگی به ارزش مکانی دارد که رقم در آن قرار گرفته است که به آن ارزش مکانی میگویم.
در جدول ارزش مکانی به ترتیب از سمت راست به چپ ،طبقه یکی، هزارها ، میلیون ها، میلیاردها قرار دارند.
هر طبقه دارای سه مرتبه یکان - دهگان - صدگان می باشد که این مرتبه ها در تمام طبقات تکرار می شوند.
در سال قبل با طبقه هزار آشنا شدیم. با گذاشتن 10 بسته ی ۱۰۰ تایی عدد هزار ساخته می شود.
10بسته هزارتایی = عدد ده هزار((10,000
10بسته ده هزارتایی = عدد صد هزار (100,000)
مثال
عدد زیر را با توجه ارزش مکانی ارقام بنویسید
782236
۲۳۶, ۷۸۲ = ۷ تا صد هزارتایی + ۸ تا ده هزارتایی+ 2 تا هزارتایی +2 تا صدتایی+3تا دهه تایی+6 تا یکی
برای گسترده کردن عدد با توجه به ارزش مکان آن رقم آن را گسترده می کنیم در جدول ارزش مکانی به جای ارقامی که نداریم صفر می گذاریم
هرچه از سمت راست به چپ حرکت کنیم ارزش رقم ها بیشتری میشود.
مثال
در عدد ۲۱۳۰۵
الف کدام رقم ارزش بیشتری دارد؟
۲ در مرتبه ده گان هزار
ب بزرگترین رقم در چه مرتبه ای قرار دارد ؟
بزرگترین رقم ۵ است در مرتبه یکان
برای خواندن اعداد از است راست سه رقم سه رقم جدا کرده و از سمت چپ سه رقم جدا شده را با عنوان طبقه می خوانیم: 526,152
پانصد و بیست و شش هزار و صد و پنجاه و دو
در نوشتن اعداد با رفتم های خواسته شده به ارزش ارقام ترجمه شود مثلاً برای نوشتن بزرگترین عدد باید بزرگترین ارقام در ارزش مکانی بیشتر یعنی از چپ به راست قرار گیرد
باید توجه داشته باشیم که صفر می تواند اولین رقم از است چپ قرار گیرد چون کمتر در سمت چپ عدد خوانده می شود.
مثال
با رقم های 4-0-5-7-2 کوچکترین و بزرگترین عدد 5 رقمی را بنویسید.
بزرگترین:
75420
کوچک ترین:
75420
یک دو چرخه سوار فاصله ی دو شهر را طی میکند. اگر او با طی کردن هر ۱۰,۰۰۰ متر در یک ایستگاه استراحت کنه با ادامه ی الگوی زیر حساب کنید پس از رسیدن به ایستگاه نهم چه مسافتی را طی کرده است؟
\(10000 - 20000 - 30000 - ...... - ........ - \)
\(10000 - 20000 - 30000 - 40000 - 50000 - 60000 - 70000 - 80000 - 90000\)
تا ایستگاه نهم 90000 متر را طی می کند.
عدد ۶۸۵ ۴۳۹ را در نظر بگیرید.
الف عدد را به حروف بنویسید.
چهارصد و سی و نه هزار و ششصد و هشتاد و پنج
ب بزرگترین رقم کدام است و چه ارزشی دارد؟
رقم 9 در جایگاه یکان هزار
ج کدام رقم بیشترین ارزش مکانی را دارد؟
رقم چهار
د کدام رقم کمترین ارزش مکانی را دارد؟
رقم 5
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم فصل 1 اعداد و الگوها
جزوه جامع ریاضی چهارم فصل 2 کسر
جزوه جامع ریاضی چهارم فصل 3 ضرب و تقسیم
جزوه جامع ریاضی چهارم فصل 4 اندازه گیری
جزوه جامع ریاضی چهارم فصل 5 عدد مخلوط و عدد اعشاری
جزوه جامع ریاضی چهارم فصل 6 شکل های هندسی
جزوه جامع ریاضی چهارم فصل 7 آمار و احتمال
الگو ها
الـگـو ها
در یک الگوی عددی با هندسی گاهی با توجه به شماره شکل و تعداد می توانیم رابطه ای کشف کرده و الگو را ادامه دهیم.
مثال
الگوها را ادامه دهید و مقدار افزایش یا کاهش الگوها را بنویسید
\(1)5 - 30 - 180 - ........ - ........ - ........ - ........ - \)
\(5\mathop \to \limits^{ \times 6} 30\mathop \to \limits^{ \times 6} 180\mathop \to \limits^{ \times 6} 1080\mathop \to \limits^{ \times 6} 6480\mathop \to \limits^{ \times 6} 38880\)
\(2)7 - 14 - 28 - ....... - ....... - ....... - ....... - \)
\(7\mathop \to \limits^{ \times 2} 14\mathop \to \limits^{ \times 2} 28\mathop \to \limits^{ \times 2} 56\mathop \to \limits^{ \times 2} 112\mathop \to \limits^{ \times 2} 224\)
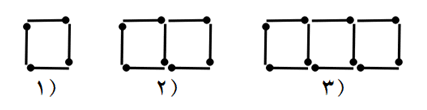
الگوی هندسی زیر را در نظر بگیرید.
الف چه رابطه ای بین شماره شکل و تعداد مربع ها وجود دارد؟
2+(3×شماره شکل)
\(5\mathop \to \limits^{ + 3} 8\mathop \to \limits^{ + 3} 11\)
ب با توجه به رابطه کشف شده حساب کنید در کدام شکل 62 مربع خواهیم داشت؟
شماره شکل: 62
188=2+(3×62)
تهیه کننده : عزیزی و حیدرزاده
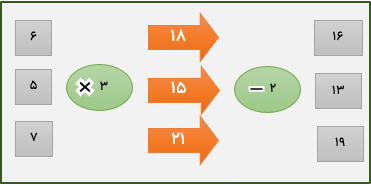
ماشین ورودی خروجی
ماشین ورودی خروجی
در این ماشین ها اعداد با توجه به نوع کاری که انجام می شود تغییر کرده و از آن خارج می شوند.
مثال
محیط مثلث متساوی الاضلاع : ۳×یک ضلع
ماشین محیط یابی:
مثال
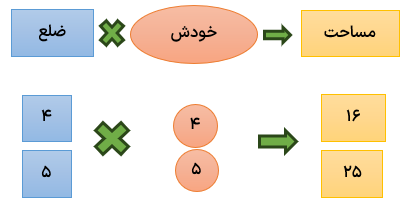
مساحت مربع : (خودش × یک ضلع)
گاهی اوقات عدد خروجی داده شده است که در این صورت باید عملیات را بر عکس انجام داده و عدد ورودی را حساب کنیم..
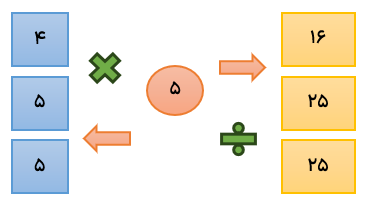
ممکن اسمت چندین عملیات وجود داشته باشد که باید در عدد ورودی به ترتیب هر مرحله را انجام دادند و با حاصل به دست آمده مرحله بعدی را انجام دهیم.
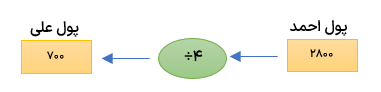
الف احمد 4 برابر علی پول دارد. اگر علی ۴۰۰ تومان داشته باشد احمد چند تومان پول دارد؟
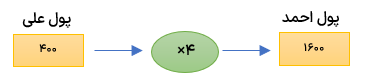
ب اگر احمد ۲۸۰۰ تومان پول داشته باشه علی چند تومان پول دارد؟
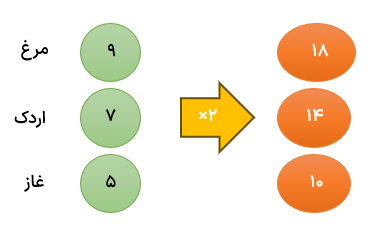
در حیاط یک خانه روستایی 9 مرغ و 7 اردک و 5 غاز وجود دارد با قرار دادن اعداد در ماشین ورودی و خروجی تعداد پاها را حساب کنید.
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
معرفی میلیون
معرفی میلیون
هر طبقه دارای ۳ مرتبه یکی _ ده تایی _ صدتایی است _ در ادامه عدد نویسی با عدد صد هزار آشنا شدیم. اگر 10 دسته ی هزار تایی در کنار هم قرار گرد عدد یک میلیون به دست می آید و یک طبقه میلیون ها به جدول ارزش مکانی اضافه می شود.
سیصد و یک میلیون و شش هزار و ده
1 هنگام قرار دادن اعداد در جدول ارزش مکانی رقم ها را با توجه به ارزش و مرتبه در جدول قرار داده و بقیه ارقامی را که نداریم صفر قرار می دهیم
2 اگر 1 واحد به بزرگترین عدد شش رقمی اضافه شود کوچکترین عدد هفت وقتی یعنی یک میلیون ساخته می شود
999999+1=1,000,000
عدد یک میلیون برابر است با 10 تا صد هزار تایی:1,000,000
عدد ده میلیون برابر است با ۱۰ تا یک میلیون تایی:10,000,000
عدد صد میلیون برابر است با 10 تا ده میلیون تایی: 100,000,000
مقایسه اعداد
مثال
الف اگر تعداد و رقم ها برابر نباشد عددی بزرگ تر است که تعداد رقم های آن بیشتر است.
\(31752\left[ > \right]5791\)
ب اگر تعداد رقم ها برابر نباشد از بزرگ ترین مرتبه یعنی از دست چپ در هر دو عدد مقایسه می شود.
3492و6578 هر دو چهار رقمی هستند ولی رقم مرتبه یکان هزار در عدد ۶۵۷۸ عدد 6 است و از رقم مرتبه کیان هزار در عدد 3۴۹۲ یعنی ۳ بزرگ تر است پس :
\(3492\left[ < \right]6578\)
مثال
الگوهای عددی زیر را ادامه دهید.
600,000 - 700,000 - ……. الف
600,000 - 700,000 – 800,000 – 900,000 – 1,000,000
10,700,000 - 10,800,000 - ……. ب
10,700,000 - 10,800,000 – 10,900,000 – 11,000,000
995,000 - 996,0000 - ……… ج
995,000 - 996,0000 – 997,000 – 998,000 – 999,000 – 1,000,000
با توجه به درد ۵۰۷۹۴۰۰۲۸ به سوالات پاسخ دهید.
الف رقم های طبقه میلیون را بنویسید.
507
ب بزرگ ترین رقم در کدام مرتبه قرار دارد؟
صدگان هزار
ج ارزش مکانی رقم 4 چیست؟
دهگان هزار
د عدد را به حروف بنویسید.
پانصد و هفت میلیون و نهصد و چهل هزار و بیست و هشت.
تفریق زیر را انجام دهید.
\(\begin{array}{l}\,\,\,\,\,8447321\\ - \,\,\,\,\,\,1\,\,2\,\,0\,0\,0\,0\\ - - - - - - - - \end{array}\)
\(\begin{array}{l}\,\,\,\,\,8447321\\ - \,\,\,\,\,\,1\,\,2\,\,0\,0\,0\,0\\ - - - - - - - - \\\,\,\,\,\,8\,5\,67321\end{array}\)
تهیه کننده : عزیزی و حیدرزاده



1736019749.png)